国内外关于弹性振动对大长径比弹箭飞行特性的影响已经有了比较深入的研究。Beal[1]将导弹简化成在尾部施加推力的均匀自由梁,分析了在定常和脉冲推力的情况下,推力和长径比对系统稳定性的影响;王良明[2]提出了大长径比弹箭弹体柔性弯曲的动力学模型和有限元模型,分析了长径比和速度等参数对弹性变形的影响;杨超和吴志刚[3]分别利用细长体理论和气动导数方法计算了导弹的非定常气动力,并对导弹气动伺服稳定性及稳定裕度进行了分析;臧涛成和胡焕性[4]对大长细比弹箭弹性效应研究进行了综述;高强[5]对弹性体导弹振动进行了主动控制研究;李家文[6]对大型捆绑火箭进行了建模、设计与分析;Du等[7]建立了“战神”火箭的动力学模型并进行了飞行仿真。但目前对于弹性特性在半物理仿真中的实现与可能带来的影响却很少涉及。本文将探讨考虑弹体弹性的导弹半物理仿真方法,建立弹性体导弹半物理仿真的数学模型,并对刚性体和弹性体导弹的数学仿真模型和半物理仿真模型进行仿真对比,分析弹性振动和转台动力学特性在弹性体导弹半物理仿真中的影响。
1 弹性体导弹的动力学模型1.1 参考系及转换矩阵为了便于描述导弹在空间中的运动,定义惯性参考系Oxyz和弹体参考系Obxbybzb分别如图 1所示。惯性参考系的原点O取在导弹发射点,Ox轴与地球表面相切且指向目标方向,Oy轴垂直于地面,以向上为正,Oz轴垂直于Oxy平面,其方向根据右手定则确定。弹体参考系的原点Ob位于导弹质心,Obxb轴与弹体纵轴重合且指向弹头方向,Obyb轴在弹体纵向对称平面内且垂直于Obxb轴,其方向以向上为正,Obzb轴垂直于Obxbyb平面,其方向按右手定则确定。
 |
| 图 1 参考系系统 Fig. 1 Reference coordinate systems |
| 图选项 |
根据欧拉角(?,ψ,γ)[8],可以确定弹体参考系相对于惯性参考系的转换矩阵。
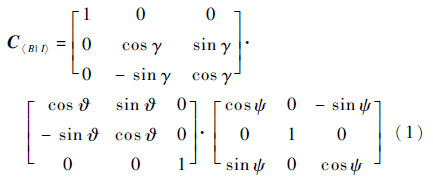
式中:C〈B丨I〉为正交矩阵,即C〈I丨B〉=C〈B丨I〉-1=CT〈B丨I〉。
1.2 动力学方程弹性体导弹在空间中的运动包括大范围平动、弹体的转动和弹性振动,类似文献[9, 10]建立弹性体导弹的动力学方程。为便于程序实现,将方程写成矩阵形式:
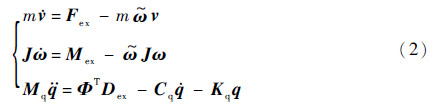
式中:m为导弹的总质量;J为导弹的惯性张量矩阵;v=[vx vy vz]T和ω=[ωx ωy ωz]T分别为导弹在弹体参考系下的平动速度和转动角速度,“~”表示计算2个张量叉积的旋转矩阵;q为弹性振动的模态坐标;Φ为弹体的模态振型的平动分量;Fex和Mex分别为导弹所受到的合外力和外力矩;Dex∈R3n×1为外力沿弹轴的分布力矩阵,其可通过将导弹划分为n个单元,计算每个单元上的外力得到;Mq、Cq和Kq分别表示模态质量矩阵、阻尼矩阵和刚度矩阵(若忽略结构阻尼,则Cq=0)。
作用在导弹上的外力包括重力、空气动力和推力,且
式中:g=[0 -g 0]T为惯性参考系下的重力加速度;Ft和Mt分别为作用在导弹上的推力和推力矩,且有
其中:P为发动机推力;x(t)为推力作用点t的坐标;Φφy(t)和Φφz(t)分别表示推力作用点yb方向和zb方向的模态振型的转动分量。
Fae和Mae分别为空气动力和空气动力矩,包括定常气动载荷和弹性振动引起的非定常气动载荷。其中,定常气动载荷有
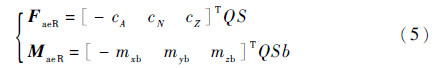
式中:Q为动压;S和b分别为导弹的参考面积和参考长度;cA、cN和cZ分别为导弹的轴向、法向和侧向气动力系数;mxb、myb和mzb分别为导弹的3个弹轴方向的力矩系数,气动力系数和力矩系数都为攻角、侧滑角、马赫数及舵偏角的函数。
弹性振动引起的非定常气动载荷可划分为弹身、弹翼和舵面分别计算,其中弹身上的非定常气动力可利用细长体理论计算[3, 11],单位长度上的纵向气动压力为
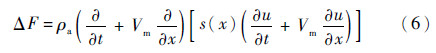
式中:ρa为空气密度;Vm为导弹的速度;s(x)为导弹横截面面积;u为弹性位移。
令
式中:S=diag(s1,s2,…,sn),sn为单元n的横截面积;L=diag(Δx1,Δx2,…,Δxn),Δxn为单元n的长度;Φy为弹体yb方向的模态振型的平动分量。则导弹弹体纵向平面内的非定常气动力、气动力矩和模态空气动力分别为
式中:Cn=(1,1,…,1),n个1;ρ0=(x1,x2,…,xn),xn为单元的xb方向坐标。
同理可得到侧向平面内的非定常气动力FaeD,L,z、气动力矩MaeD,L,y和模态空气动力QaeD,L,2。则弹身上的非定常气动载荷为
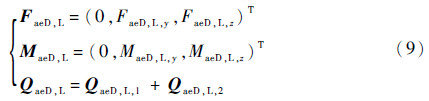
对于弹翼和舵面,由弹性变形产生的附加攻角、侧滑角和舵偏角分别为
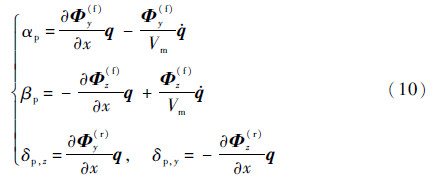
式中:Φy(f)、Φy(r)、Φz(f)和Φz(r)分别为弹翼和舵面处yb和zb方向的模态振型的平动分量。则舵面和弹翼上的附加气动载荷分别为
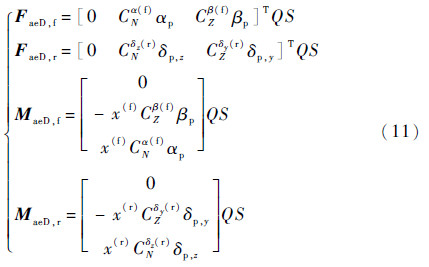
式中:CNα(f)和CZβ(f)分别为弹翼上法向气动力系数对攻角的偏导和侧向气动力系数对侧滑角的偏导;CNδz(r)和CZδy(r)分别为舵面处法向气动力系数和侧向气动力系数对舵偏角的偏导;x(f)和x(r)分别为弹翼和舵面位置的坐标。
则弹性振动引起的非定常气动力为
式中:Φ(f)和Φ(r)分别为弹翼和舵面处的模态振型的平动分量。
综合以上各式得到弹性体导弹的动力学方程为
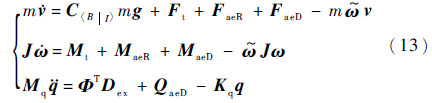
1.3 控制方程仅考虑导弹纵向平面内运动,若导弹采用过载自动驾驶仪,其控制方程可以表示为[12, 13]
式中:
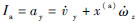为加速度信号,vy和ay分别为y方向的速度和加速度;ωz为z方向的角速度;K1、ka和kg分别为自动驾驶仪、加速度计和角速度陀螺的放大系数。Iω=ωz为角速度信号;x(a)为加速度计到质心的距离;当采用比例导引法制导时,指令信号ac为
式中:
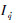为视线角速度信号;N为导引系数;Vr为导弹与目标间的相对速度。在弹性体导弹飞行过程中,由于弹体的弹性振动,导弹上敏感器件所测量的信号将受到干扰,实际测量到的角速度信号和加速度信号分别为
式中:Φφz(g)和Φy(a)分别为角速率陀螺处的模态振型的转动分量和加速度计位置处的模态振型的平动分量。则弹性体模型的控制方程为
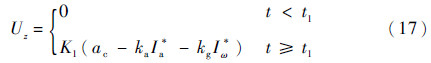
通过结合式(13)和式(17),就建立了弹性体导弹的数学仿真模型。为了便于后文中对导弹的弹性体和刚性体模型进行仿真对比分析,通过消去弹性项,可以建立刚性体导弹的数学仿真模型。
2 半物理仿真系统数学模型本节将建立导弹半物理仿真系统的数学模型,分别包括仿真计算机、三轴转台、角速率陀螺、加速度计、自动驾驶仪、舵机和导引头,仿真流程如图 2所示[14]。
 |
| 图 2 半物理仿真流程 Fig. 2 Flowchart of hardware-in-the-loop simulation |
| 图选项 |
对于弹性体导弹,在半物理仿真时模拟弹体弹性特性对弹上惯性器件的影响,有利于提高仿真精度。但直接利用转台模拟弹体的弹性振动较难实现,可采用数字注入的方式将弹性振动量叠加在角速率陀螺和加速度计的测量信号之上,以代替受弹性振动干扰的敏感器件测量信号。
2.1 仿真计算机仿真计算机中包含第1.2节中建立的导弹的动力学方程以及目标的运动方程。通过采集舵信号,解算导弹的各状态参数,并将目标信号、姿态角信号和加速度信号分别传递给导引头、转台和加速度计[15]。
2.2 自动驾驶仪自动驾驶仪的数学模型即第1.3节中建立的控制方程,刚性体模型和弹性体模型分别对应式(14)和式(17)。与数学仿真模型不同的是,半物理仿真模型输入的加速度信号、角速度信号和指令信号均为经加速度计、角速度陀螺和导引头测量的信号,应分别包含加速度计、角速度陀螺和导引头的动力学环节。
2.3 转台转台的输入信号为?,输出为φ,其传递函数可以简化为二阶环节,
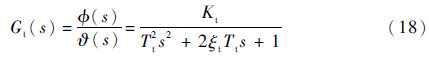
式中:Kt、Tt和ξt分别为转台传递函数的增益、固有周期和阻尼比。
2.4 弹上器件[8]1)角速度陀螺仪
输入信号为转台框架的转动角速度ωφ,其传递函数为
式中:Kg、Tg和ξg分别为加速度计传递函数的增益、固有周期和阻尼比。
对于弹性体模型,注入弹性量,得到Iω*=Iω+Φ(g)φz
。2)加速度计输入信号为仿真计算机仿真计算出的加速度ay,其传递函数为
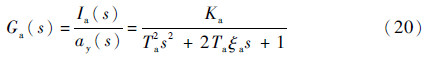
式中:Ka、Ta和ξa分别为加速度计传递函数的增益、固有周期和阻尼比。
对于弹性体模型,注入弹性量，使I*a=Ia+Φy(a)
。3)导引头
输入信号为视线角qε,输出信号为视线角速度信号
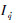,其传递函数为
式中:Ks、Ts和ξs分别为引导头传递函数的增益、固有周期和阻尼比。
4)舵机
输入信号为控制系统传来的控制信号Uz,输出为舵面实际偏转的舵偏角δz,其传递函数简化为惯性环节,
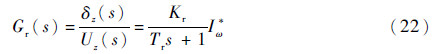
式中:Kt和Tr分别为舵机传递函数的增益和固有周期。
2.5 半物理仿真的状态空间模型第2.1~2.4节各个半物理仿真设备的传递函数可以改写为统一的状态空间方程形式:
式中:X为状态量;Y为仿真设备的输出量;A、B、C和D为系数矩阵;u为仿真设备的输入量。通过将弹性体导弹的动力学方程和仿真设备的状态方程联立,就建立了弹性体导弹的半物理仿真模型,通过消去弹性项可以建立刚性体导弹的半物理仿真模型。后文将以上建立的4种模型集成到整体的仿真框架中,实现考虑半物理仿真设备动力学特性的一体化仿真。
3 算例为了分析弹体弹性特性和转台动力学特性在弹性体导弹半物理仿真中的影响,需要分别得到第1节和第2节所建立4种模型的仿真结果,并进行对比分析。为方便表述,定义如表 1所示的4种工况。
表 1 算例工况描述Table 1 Case description of example
| 编号 | 工况 | 符号 |
| 1 | 刚性体数学仿真模型 | RMS |
| 2 | 弹性体数学仿真模型 | FMS |
| 3 | 刚性体半物理仿真模型 | RHILS |
| 4 | 弹性体半物理仿真模型 | FHILS |
表选项
为简化算例,本文仅对导弹铅垂平面内的运动进行仿真,目标匀速在2 km高度的水平面内飞行,算例导弹的基本参数如表 2所示,经有限元计算,其前三阶频率依次为13.1、34.3和58.7 Hz。分别对RMS、FMS、RHILS和FHILS 4种工况进行仿真,为说明仿真设备在刚性体和弹性体仿真中所起作用的不同,首先对比RMS和RHILS的仿真结果,得到RMS和RHILS2种工况的弹道曲线、俯仰角曲线和俯仰角速度曲线如图 3所示。可以看到2种工况的3条曲线差别极小,说明对于刚性体导弹,其半物理仿真模型的仿真结果与纯数学仿真模型的仿真结果并没有较大差别,转台等仿真设备能够较好地响应输入信号,对仿真结果的影响很小。
表 2 算例导弹基本参数Table 2 Main parameters of missle example
| 参数 | 数值 | 参数 | 数值 |
| 导弹质量/kg | 304 | 弹翼根弦长/m | 0.68 |
| 导弹长度/m | 4.64 | 弹翼梢弦长/m | 0.53 |
| 弹身直径/m | 0.25 | 弹翼展长/m | 0.44 |
| 头部长度/m | 0.58 | 舵面弦长/m | 0.18 |
| 尾部长度/m | 0.32 | 舵面展长/m | 0.44 |
表选项
 |
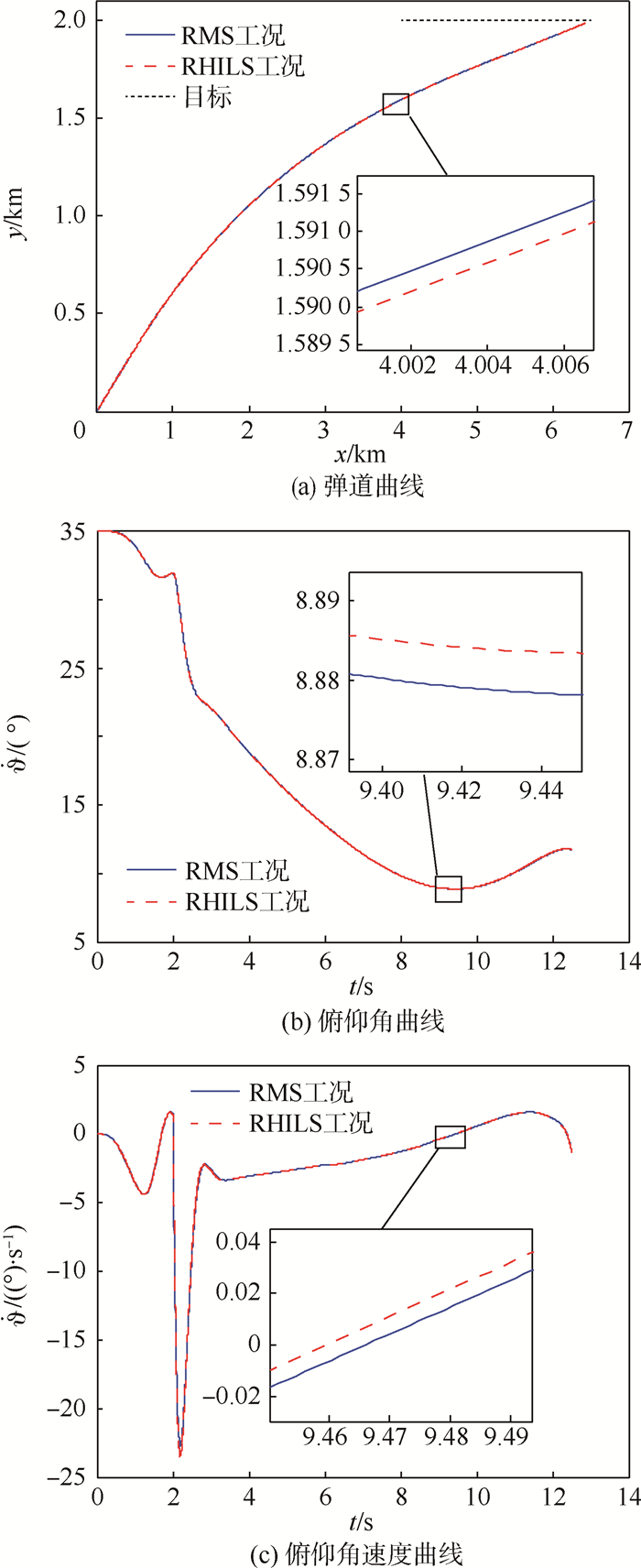| 图 3 RMS和RHILS 2种工况的弹道、俯仰角及俯仰角速度曲线 Fig. 3 Curves of trajectory, pitching angle, and pitching angular velocity of two examples of RMS and RHILS |
| 图选项 |
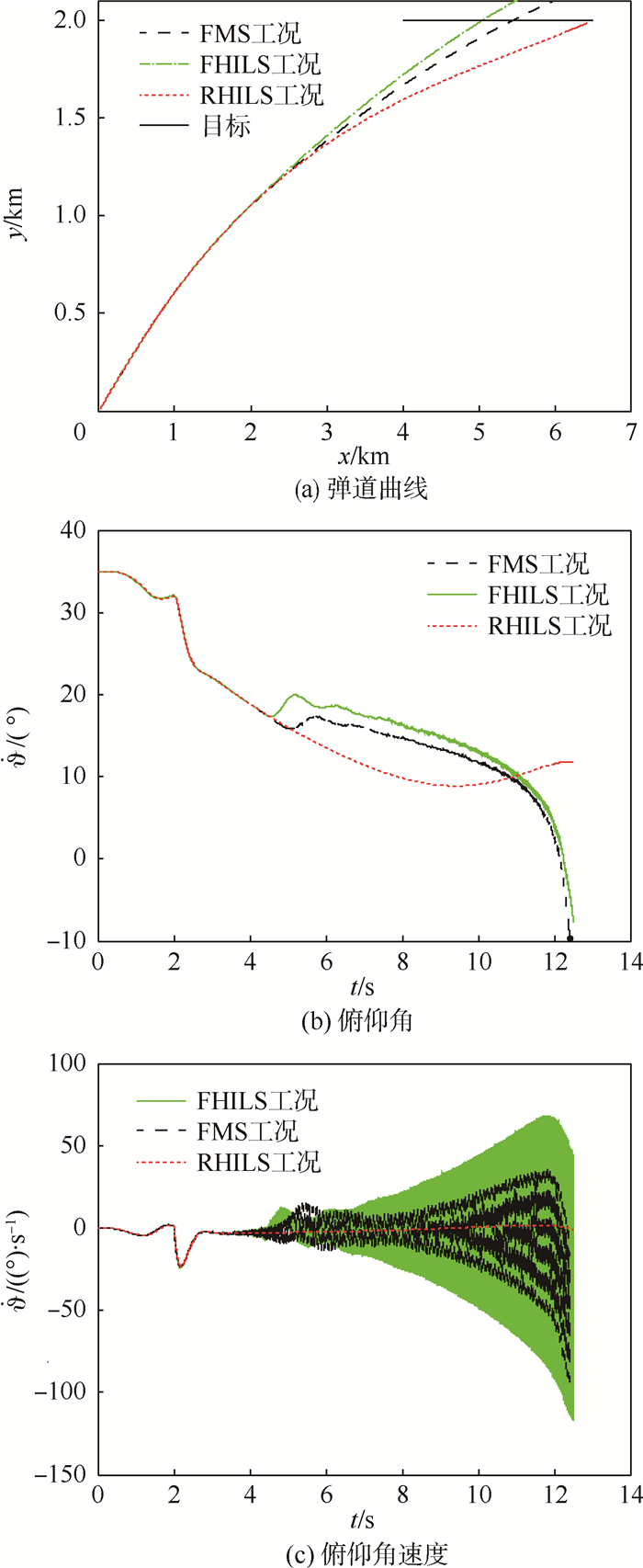
对比FMS、RHILS和FHILS 3种工况的仿真结果,得到一系列曲线如图 4所示。
 |
| 图 4 FMS、RHILS和FHILS 3种工况的弹道、俯仰角及俯仰角速度曲线 Fig. 4 Curves of trajectory, pitching angle, and pitching angular velocity of three examples of FMS, RHILS and FHILS |
| 图选项 |
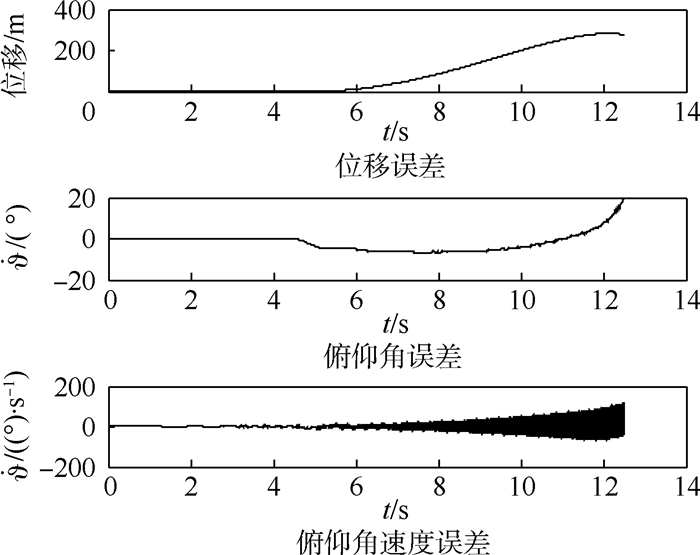
图 4中,RHILS和FHILS2种工况的3条仿真曲线具有较大的差别,其误差如图 5所示。其中弹道曲线的最大误差为282 m,FHILS的俯仰角曲线和俯仰角速度曲线呈现了明显的弹性振动现象,俯仰角速度曲线在4 s后趋于发散。2种工况的仿真结果表明,弹性特性在半物理仿真中产生了较大影响,在大长径比导弹的半物理仿真中考虑弹性特性是具有现实意义的。
 |
| 图 5 RHILS和FHILS误差曲线 Fig. 5 History of errors between RHILS and FHILS |
| 图选项 |
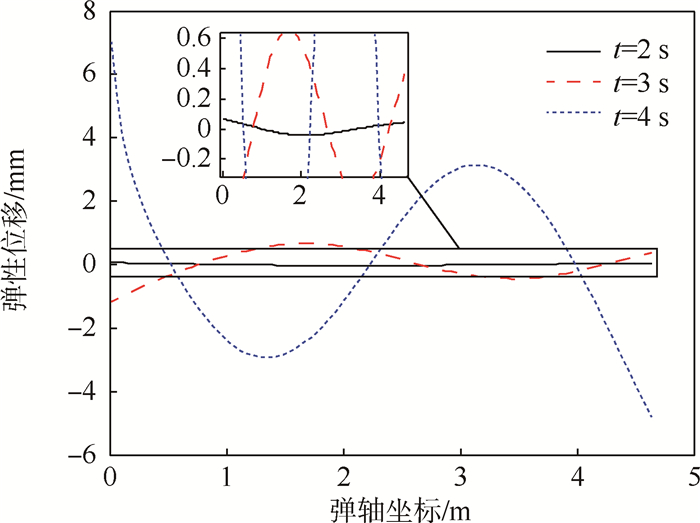
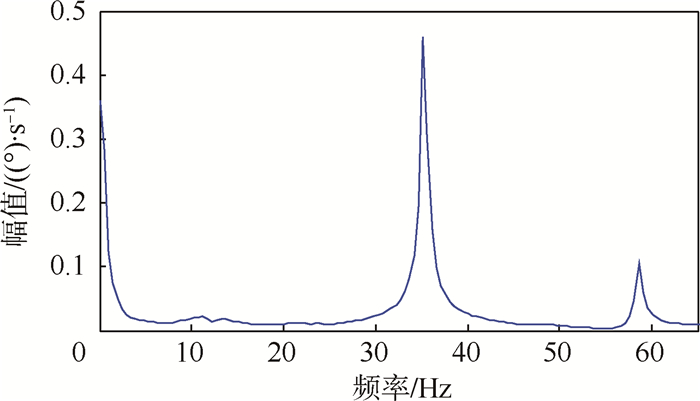
对比FMS和FHILS2种工况,可以看到弹性体模型的半物理仿真和数学仿真的弹道曲线具有一定的差别,俯仰角曲线和俯仰角速度曲线具有相近的变化趋势,但半物理仿真模型的俯仰角速度的振动幅值大于数学仿真模型。如图 6所示,导弹在3 s后的变形曲线与二阶振型相近,同时对图 4(c)中FMS工况的俯仰角速度曲线进行频域分析,其最大峰值处的频率为34.2 Hz(如图 7所示)。这说明3 s后第2阶频率(34.3 Hz)在弹性振动中起主导作用,而转台的截止频率为32.6 Hz,说明转台动力学与弹性体导弹动力学产生了耦合效应,使半物理仿真中弹性振动现象得到放大。因此对弹性体导弹进行半物理仿真时,应该考虑仿真设备动力学特性的影响,仿真设备可能将放大或削弱弹性振动效应,影响半物理仿真的精度。
 |
| 图 6 导弹各时刻变形曲线 Fig. 6 Deformed curves of missile at each moment |
| 图选项 |
 |
| 图 7 3 s之后俯仰角速度的频率特性曲线 Fig. 7 Curve of pitching angular velocity in frequency domain after 3 s |
| 图选项 |
4 结 论1)对大长径比导弹进行半物理仿真时,其弹性特性不可以被忽略,考虑弹性振动有利于提高大长径比导弹半物理仿真的精度。
2)在半物理仿真中,转台等仿真设备的动力学特性会对弹体的弹性振动效应产生影响。因此,在对弹性体导弹进行半物理仿真实验时,应该考虑转台动力学特性的影响,采用合适带宽的转台有利于半物理仿真精度的提高。
3)由于高精度、大长径比导弹研发需求的提高,实现考虑弹体弹性的导弹半物理仿真的新方法和新途径可能会成为未来弹性飞行器领域的研究热点之一。
参考文献
| [1] | BEAL T R. Dynamic stability of a flexible missile under constant and pulsating thrusts[J].AIAA Journal,1965,3(3):486-494. |
| Click to display the text | |
| [2] | 王良明. 大长径比弹箭在飞行时的柔性变形特性分析[J].兵工学报,2000,21(2):108-111. WANG L M.An analysis on the flexibility in flight of projectiles or rockets having high L/D ratios[J].Acta Armamentarii,2000,21(2):108-111(in Chinese). |
| Cited By in Cnki (17) | |
| [3] | 杨超,吴志刚. 导弹气动伺服弹性稳定性分析[J].飞行力学,2000,18(4):1-5. YANG C,WU Z G.Aeroservoelastic stability of missile[J].Flight Dynamics,2000,18(4):1-5(in Chinese). |
| Cited By in Cnki (24) | |
| [4] | 臧涛成,胡焕性. 大长细比弹箭弹性效应研究综述[J].弹道学报,1999,11(3):89-93. ZANG T C,HU H X.A review of great slenderness ratio projectile elastic effect research[J].Journal of Ballistics,1999,11(3): 89-93(in Chinese). |
| Cited By in Cnki (13) | Click to display the text | |
| [5] | 高强. 弹性体导弹振动主动控制研究[D].合肥:中国科学技术大学,2009:1-55. GAO Q.Active vibration control of flexible missiles[D].Hefei:University of Science and Technology of China,2009:1-55(in Chinese). |
| Cited By in Cnki (7) | |
| [6] | 李家文. 大型捆绑火箭姿态控制系统的建模、设计与分析[D].长沙:国防科学技术大学,2011:1-147. LI J W.Modeling, design and analysis of large strap-on launch vehicle's attitude control system[D].Changsha:National University of Defense Technology,2011:1-147(in Chinese). |
| Cited By in Cnki (1) | |
| [7] | DU W,WIE B, WHORTON M.Dynamic modeling and flight control simulation of a large flexible launch vehicle[C]//Proceedings of AIAA Guidance,Navigation and Control Conference and Exhibit,2008.Reston:AIAA,2008:AIAA-2008-6620. |
| [8] | 孟秀云. 导弹制导与控制系统原理[M].北京:北京理工大学出版社,2003:35-91. MENG X Y.Principle of missile guidance and control system[M].Beijing:Beijing Institute of Technology Press,2003:35-91(in Chinese). |
| [9] | WASZAK M R, SCHMIDT D K.Flight dynamics of aeroelastic vehicles[J].Journal of Aircraft,1988,25(6):563-571. |
| Click to display the text | |
| [10] | SCHMIDT D K, RANEY D L.Modeling and simulation of flexible flight vehicles[J].Journal of Guidance,Control and Dynamics,2001,24(3):530-546. |
| Click to display the text | |
| [11] | CHAE S, HODGES D H.Dynamics and aeroelastic analysis of missiles[C]//Proceedings of 44th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Reston:AIAA,2003:AIAA-2003-1968. |
| [12] | 李玉林,李晅, 杨树兴.过载自动驾驶仪分析研究[J].战术导弹技术,2008(5):63-68. LI Y L,LI X,YANG S X.Analysis of lateral acceleration autopilot[J].Tactical Missile Technology,2008(5):63-68(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [13] | 魏先利,夏群力, 祁载康.姿态及过载自动驾驶仪比例导引对比研究[J].弹箭与制导学报,2003,23(4):5-8. WEI X L,XIA Q L,QI Z K.Comparison study of proportional navigation guidance law of attitude and acceleration autopilot[J].Journal of Projectiles,Rockets,Missiles and Guidance,2003,23(4):5-8(in Chinese). |
| Cited By in Cnki (12) | Click to display the text | |
| [14] | 单家元,孟秀云, 丁艳.半实物仿真[M].北京:国防工业出版社,2008:18. SHAN J Y,MENG X Y,DING Y.Hardware-in-the-loop simulation[M].Beijing:National Defense Industry Press,2008:18(in Chinese). |
| [15] | 毕业. 导弹半实物仿真系统误差分析[D].西安:西北工业大学,2006:19-20. BI Y.Error analysis of missile's hardware-in-the-loop simulation system[D].Xi'an:Northwestern Polytechnical University,2006:19-20(in Chinese). |
| Cited By in Cnki (9) |
