小视场(Narrow Filed of View, NFOV)星敏感器成本较低，并且在极端天气下更加适用，因此小视场星敏感器的姿态估计算法具有重要的研究价值。通过对导航星表进行预处理，导致星图识别过程中识别时间增加，影响星敏感器输出信息的时间，造成量测延时问题。同时，光学系统以及确定姿态等步骤的繁琐性，也导致了姿态敏感器输出信息的同时带有延时现象。
延时问题的存在，导致系统模型中存在了不确定性。鲁棒滤波算法被证实是一种处理模型不确定性问题的有效算法^[1-3]。文献[4]讨论了针对有界模型不确定的线性时域系统二阶鲁棒卡尔曼滤波(Robust Kalman Filter，RKF)算法，但该模型不适用于非线性系统。文献[5]提出鲁棒扩展卡尔曼滤波(Robust Extended Kalman Filter，REKF)算法，通过预测-校正形式估计刚体姿态，所提出的姿态估计系统考虑四元数刚体模型，其建模时主要考虑的是加性噪声，但其不适于乘性耦合噪声的环境。文献[6]设计了一种RKF算法处理乘性耦合噪声，但其不能很好地解决量测延时带来的影响。文献[7]设计了一种RKF算法用于处理状态延迟与量测丢失的时变离散系统，通过求取状态估计协方差的最小上界来计算需要的参数。文献[8]提出了鲁棒有界时域滤波(Robust Finite Horizon Filter，RFHF)算法用于解决确定概率分布情况的延迟系统。但是文献[7-8]这2种算法只适用于线性系统。文献[9]提出了基于5阶球半径规则的容积卡尔曼滤波算法，使其更适用于非线性系统，解决传感器随机延时的问题，然而该算法在建模时没有考虑乘性耦合噪声，且与本文所研究的实际情况并不相符。
因此，针对小视场星敏感器与陀螺仪结合的模型，本文提出了REKF算法用于处理量测延时因素引起的模型不确定情况。通过状态扩维理论获得带有量测延时的非线性系统模型，并且建立的系统模型包含乘性耦合噪声。根据最小方差准则近似确定估计误差方差的最小上界范围，通过该最小上界选取滤波增益参数，从而得到量测延时情况下的REKF算法。仿真结果表明，本文算法所能达到的估计精度较原有算法有明显提高。
1 组合姿态算法设计 1.1 系统模型
1.1.1 陀螺的量测模型 在姿态估计系统中，陀螺仪用来测量卫星转过角速率的姿态敏感器。陀螺仪产生的误差因素有很多，如失准角误差、标度因素误差、漂移误差、时间延迟等。大部分的误差可以通过校正来补偿，而随机漂移、噪声因素等是主要的误差源，故陀螺量测模型可表示为^[10]

(1)

式中：为测量到的陀螺角速率；ω为真实的陀螺角速率；b为陀螺漂移；η_u和η_v分别为陀螺漂移噪声和陀螺测量噪声，它们是互相独立的、均值为零、服从高斯分布的高斯白噪声，σ_u²、σ_v²表示对应的方差。

1.1.2 星敏感器的量测模型 用四元数来表示量测模型为

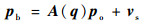(2)

式中：A(q)=C_o^b，C_o^b为轨道坐标系到本体坐标系之间的姿态矩阵，C_i^o为惯性坐标系到轨道坐标系之间的姿态矩阵；v_s为星敏感器测量白噪声，服从N(0, σ_s²)；p_o为轨道坐标系下的矢量坐标; p_b为本体坐标系下的输出矢量。
1.2 状态方程与量测方程 由四元数轨道动力学方程可得

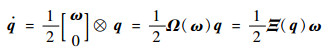(3)

式中：ω=[ω_x??ω_y??ω_z]^T为输出的陀螺角速率；q=[q₁??q₂??q₃??q₄]^T=[ρ??q₄]^T为真实四元数；，[ω×]表示ω的反对称矩阵，；Ξ(q)= 。
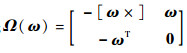
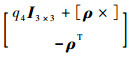
为了给出具体的状态方程与量测方程，需选取状态量。这里选取k时刻姿态四元数q_k和陀螺漂移b_k作为状态变量，即x_k=[q^T_k??b^T_k]^T，那么离散化后的状态方程为

(4)

式中：

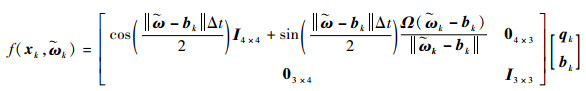ω_k为满足均值为零、方差为Q_k= 的高斯白噪声；为乘性噪声项，s取3，η_ik表示均值为零、方差为1的噪声，A_ik表示有适当阶数的确定矩阵：

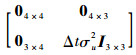
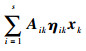
(5)

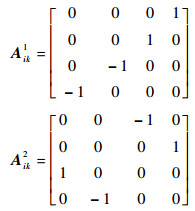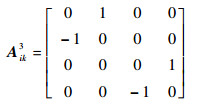根据式(2)，选取星敏感器输出的姿态四元数作为量测变量，选取3个参考矢量描述姿态估计系统，故系统的量测模型为

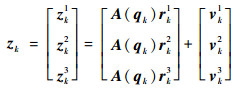(6)

式中：r_kⁱ为星敏感器在参考坐标系下对应的参考向量；v_kⁱ为满足均值为零、方差为R_k=σ_s²I_3×3的高斯白噪声。
由于星敏感器进行姿态估计时存在量测延时现象，上述建立的星敏感器量测模型没有考虑延时的存在，使得输出结果并不准确，笔者考虑一步延时的星敏感器量测模型：

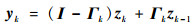(7)

式中：y_k为k时刻真实的量测量；Γ_k为不同的延迟速率，Γ_k=diag{[μ_{k, 1}??μ_{k, 2}…??μ_{k, m}]}，μ_{k, i}(i=1, 2，…，m)服从伯努利分布(0~1分布)，满足：

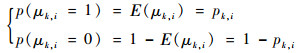(8)

故根据式(4)、式(6)、式(7)可以得出关于量测延时及乘性噪声的非线性离散系统：

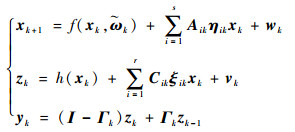(9)

式中：C_ik为有恰当维数的已知矩阵; ξ_ik为均值为零、方差为1的噪声; v_k为零均值高斯白噪声。由于实际的量测输出y_k与z_k、z_k－1两个时刻的量测量均相关，需要利用状态扩维理论，使其得到相同时刻量测量的表达式。

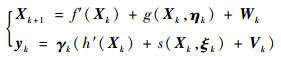(10)

式中：






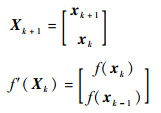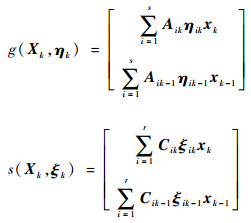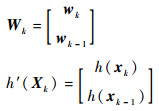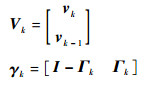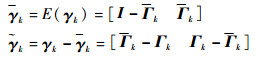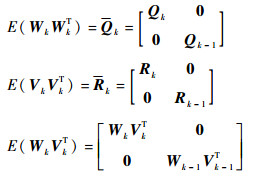Γ_k=diag{p_{k, 1}??p_{k, 2}…??p_{k, m}}，由Γ_k的分布特性可知，是一个零均值的随机矩阵序列。由文献[11]可知，h(x_k)满足:

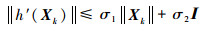(11)

式中：σ₁、σ₂为非负标量。
2 鲁棒扩展卡尔曼滤波算法 针对带有量测延时及乘性噪声的离散系统式(9)，经过状态扩维理论，获得一个相对简单的模型式(10)，提出改进的REKF算法，并且计算预测方差，给出估计误差方差的最小上界。
一步状态预测

(12)

状态更新

(13)

式中：为在时间k处扩维后的状态估计；为在时间k+1处的一步预测；K_k+1为滤波器增益。
根据以上分析，对于带有乘性噪声及量测延时的不确定性系统，就是设计式(10)的REKF算法的问题。由于实际的误差方差难以求出，只能通过确定滤波增益参数来确保误差方差的最小上界，即

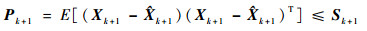(14)

2.1 估计误差方差 在REKF算法中，通过选取一些模型不确定参数来表示其对系统的影响。与EKF算法类似，需要对状态函数与量测函数进行泰勒展开，主要区别在于根据上界范围进行滤波器的具体设计。通过这样的计算，使得求得的精度、效果等相较于EKF算法更优良。
一步状态预测误差可写为

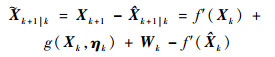(15)

扩维后的状态函数f′(X_k)通过在点处泰勒展开，得到

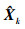
(16)

式中：; 为经过展开后的高阶项。引入未知时变矩阵β_k∈R^n×n，满足β_k· β^T_k=I_n×n，具体的缩放矩阵B_k∈R^n×n，L_k表示已知的调节矩阵，故高阶项可表示为^[12]

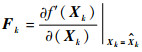
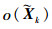
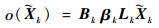(17)

将式(16)、式(17)代入式(15)可得

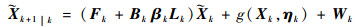(18)

由于η_ik服从高斯分布，不同时刻之间是互相独立的，其相关性为0。而η_ik与w_k是互相独立的高斯白噪声，均值为零。故一步预测误差方差矩阵可表示为

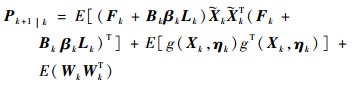(19)

式中：

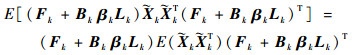(20)

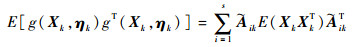(21)

其中：。
式(19)可简化表示为

(22)

已知k+1时刻的状态估计误差与真实值和估计值有关，可以表示为

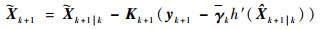(23)

将式(10)代入式(23)中，可以得到

(24)

同式(16)相同，对量测函数泰勒展开，保留高阶项，并代入式(24)得

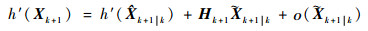(25)

式中：；，根据文献[13]，α_k+1为未知的时变矩阵，D_k+1为考虑不确定系统模型误差的比例矩阵。
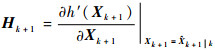
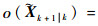
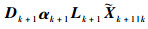
将式(25)代入式(24)中，所以有

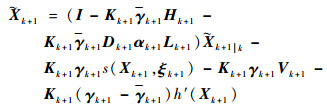(26)

将式(26)代到式(14)中，得到滤波误差方差矩阵，表示为

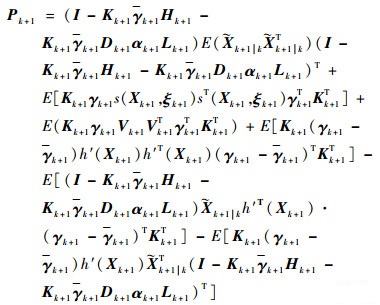(27)

由式(22)、式(27)可以得到方差矩阵P_k+1|k、P_k+1，因为所建立的系统模型考虑了乘性噪声及量测延时等不确定性因素，其中包括未知矩阵如β_k、α_k+1，所以并不能实际求出协方差的具体值。根据最小方差准则的要求，求取预测误差方差P_k+1|k和滤波更新误差方差P_k+1的最小上界来近似替代。
2.2 算法设计 根据文献[14]中的2条引理(引理6.1、引理6.2)构造上界范围，并且可以求得滤波更新误差方差矩阵P_k+1的最小上界。
这里引入二阶矩的概念。若对于任意的t属于T，若E[X²(t)]存在，则称X(t)为二阶矩过程。实际就是对变量的平方求期望，所以二阶矩的值是大于等于零的。假设ε₁为正数，那么的二阶矩一定大于等于零。所以有

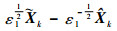
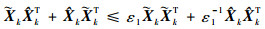(28)

根据式(28)可以得到

(29)

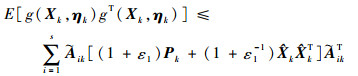(30)

假设存在正数λ和矩阵L_k，满足条件0.5λ^-1·I-L_kP_kL^T_k>0，由文献[15]中的引理可推导出

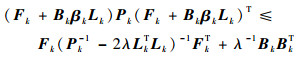(31)

将式(29)~式(31)代入到式(22)中，可以求出一步预测误差方差矩阵的上界：

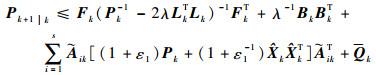(32)

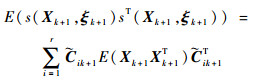(33)

将式(33)代入式(27)，得到滤波误差方差矩阵为

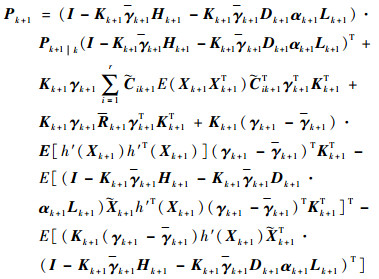(34)

式中：。
同理，根据二阶矩原理，假设存在正数ε₂，同样能求解得到

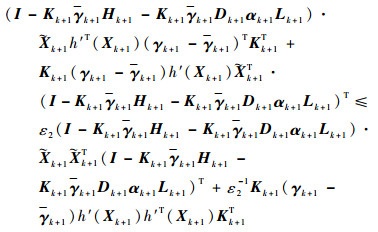(35)

由式(15)可得到

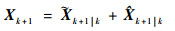(36)

假设存在正数ε₃，同样能求解得到

(37)

所以有

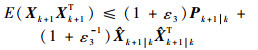(38)

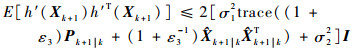(39)

假设存在正数μ和矩阵L_k+1，满足条件μ^-1I－L_k+1P_k+1|kL_k+1^T>0，能够推出

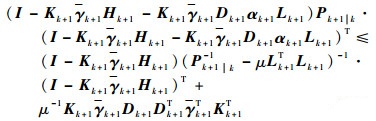(40)

所以，k+1时刻的更新后状态误差的方差矩阵为

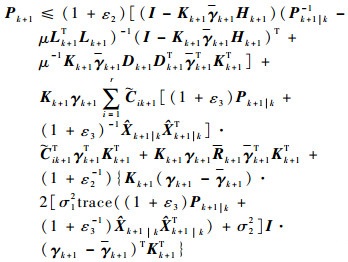(41)

根据式(32)、式(41)得到了一步预测方差和滤波更新方差的上界，当ε₁、ε₂、ε₃、λ、μ都是正数时，提出以下2个离散Riccati方程：

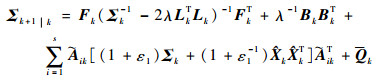(42)

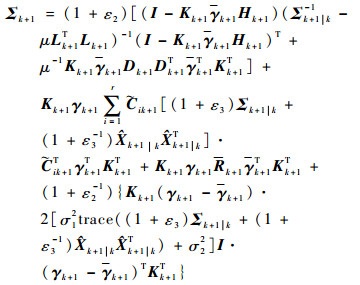(43)

用数学归纳法证明Σ_k+1|k、Σ_k+1是P_k+1|k、P_k+1的上界范围，即

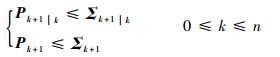(44)

在初始k=0时刻，能够轻易求出P₀=Σ₀>0，根据不等式(29)、式(30)以及等式(43)可得

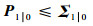(45)

由式(45)及式(44)中的第一项可以得出

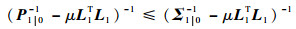(46)

由式(45)和式(46)，可以推断出k=0时刻的状态误差方差满足：

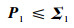(47)

选取k=n－1时刻，假设满足不等式P_n≤Σ_n，那么当k=n时，同式(46)类似，有

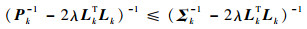(48)

因此，根据式(44)可以得出

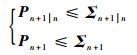(49)

根据构造的P_k+1|k和P_k+1的最小上界确定最优的滤波增益。对式(43)K_k+1项求偏导确定滤波增益的最优值：

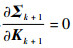
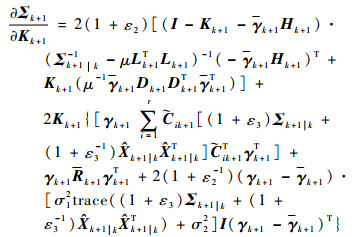(50)

(51)

设计滤波器的目的是根据状态模型和不同观测量中的信息计算状态变量的估计值，达到状态量的估计值与真实值误差最小，精度最高；在滤波设计过程中，需要权衡多种不同信息，充分合理地利用这些信息。REKF的设计是基于不确定的系统模型进行的，REKF算法的性能在于不确定性模型是否能完整描述实际系统。为了获得理想的滤波效果，式(1)给出的不确定性模型需要准确给出不确定性参数的大小。
3 仿真实验与分析 3.1 仿真环境 为了验证REKF算法的有效性，本节仿真利用传统的加性扩展卡尔曼滤波(AEKF)算法、RKF算法^[6]、RFHF算法^[8]与本文所提的REKF算法进行比较。实际的星敏感器精度较高，可以把泰勒展开得到的高阶项忽略，B_k、D_k+1设置为0。调节矩阵。为了保证系统能达到的精度，参数λ和μ均设置为0.000 1，参数ε设置为0.1。通过状态模型及量测模型可知，其中包括加性噪声，考虑噪声及延时对系统的影响，可令矩阵C_ik=0。仿真时间设为1 h，量测模型参数σ_ij=10 s(i=1, 2, 3;j=x, y, z)。
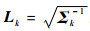
3.2 仿真分析 1) 情况1
不考虑系统存在延时情况并且假设姿态角及陀螺漂移部分均没有误差存在。假设卫星以角速率ω(t)=[4π/3 ??0??0]^T rad/s旋转，初始三轴姿态角设为[0??0??0]^T(°)，卫星轨道角速度Ω₀=0.001 rad/s。常值漂移设为0.1 (°)/h，漂移噪声设为，测量噪声设为。星敏感器的测量噪声设为σ_s=0.005°。初始状态值为x₀=[0??0??0??1??0.1??0.1??0.1]^T，对应的初始四元数部分为q₀=[0??0??0??1]^T，初始陀螺漂移部分为β₀=[0.1??0.1??0.1]^T(°)/h，星敏感器的3个参考矢量设为r₁=[1??0??0]^T，r₂=[0??1??0]^T，r₃=[0??0??1]^T。星敏感器与陀螺的采样频率为1 Hz。初始的3个姿态角误差方差矩阵表示为0.01I_3×3(°)²，陀螺漂移的误差方差矩阵表示为0.04I_3×3((°)/h)²。
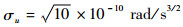
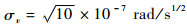
从图 1和图 2可以看出，当假设系统不存在延时情况时，各滤波算法的性能相差不大，基本都能达到0.000 1°左右的精度。整体来看，REKF算法和RKF算法要略优于AEKF算法和RFHF算法，这是由于AEKF算法和RFHF算法在设计时都没有考虑到乘性噪声的影响，导致它们在非线性估计时存在一定误差，因此滤波精度稍差。

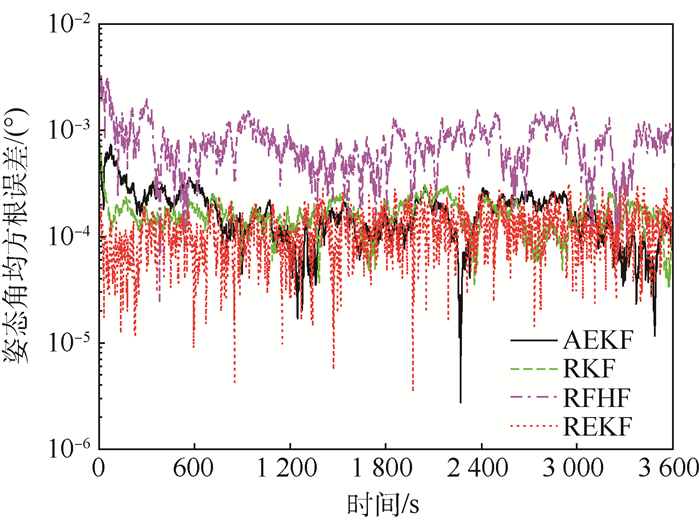图 1 情况1时姿态角均方根误差对比 Fig. 1 Comparison of root mean square error of attitude angle in Case 1

图选项

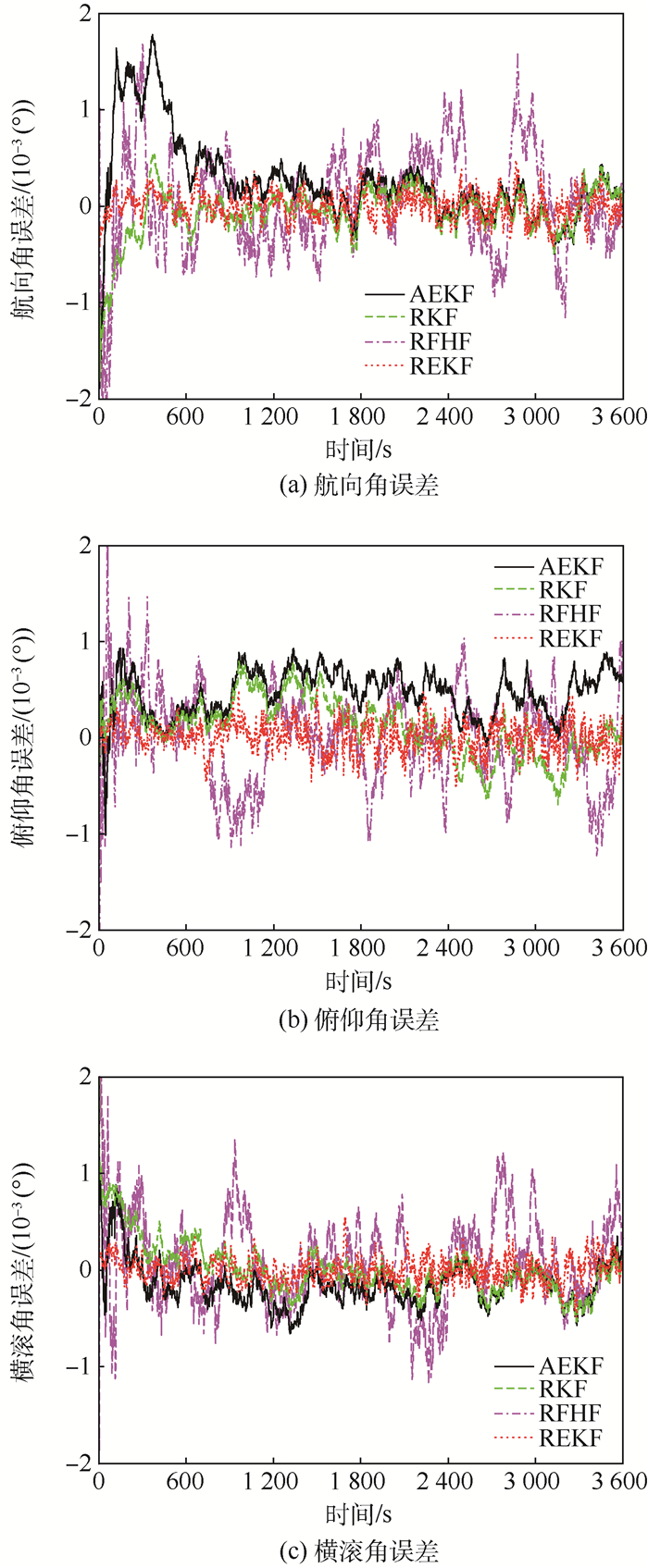图 2 情况1时姿态角误差对比 Fig. 2 Comparison of attitude angle error in Case 1

图选项

2) 情况2
假设星敏感器工作时出现延时现象，设3个方向的矢量延时速率各不相同的，并且满足伯努利分布：Γ_k=diag{[0.2 ??0.2 ??0.2 ??0.1 ??0.1 ??0.1??0.05 ??0.05 ??0.05]}
从图 3和图 4可以看出，REKF算法处理带有延时及乘性噪声的非线性系统的效果要明显优于RFHF算法、RKF算法及AEKF算法，这是因为建立了带有乘性噪声和延时的误差模型来表示这种情况，而AEKF算法并不适用带有延时的系统，RKF算法只能满足乘性噪声项所带来的干扰，但没有考虑延时问题。所以，当出现延时时，RKF算法并不能保证系统精度，甚至会带来滤波发散。而RFHF算法只考虑了量测延时和量测丢失，没有考虑乘性噪声的影响，因此，在具有乘性噪声的实验环境下不能达到最理想的状态。

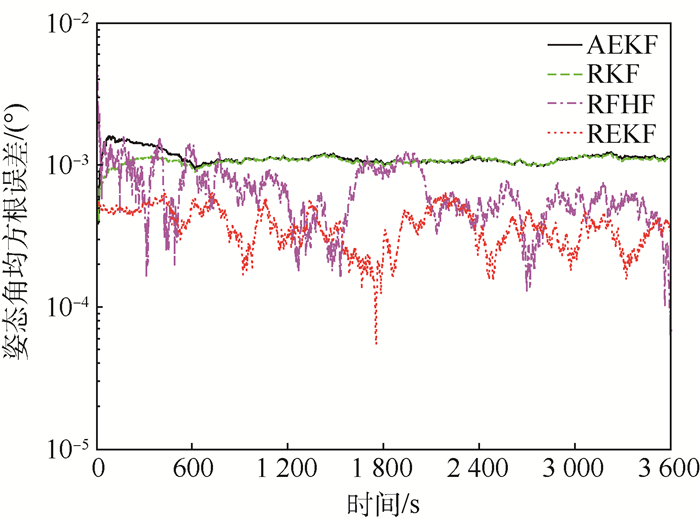图 3 情况2时姿态角均方根误差对比 Fig. 3 Comparison of RMSE of attitude angle in Case 2

图选项

图 4 情况2时姿态角误差对比 Fig. 4 Comparison of attitude angle error in case 2

图选项

4 结论 针对小视场星敏感器姿态估计时存在的信息延时问题，本文做了如下研究：
1) 建立带有延时不确定项的误差模型，该模型考虑到非线性系统同时存在乘性噪声及量测模型延时的情况，对REKF滤波算法进行改进。
2) 在算法设计时，根据最小均方误差准则要求，通过求取预测误差方差和滤波更新误差方差的最小上界进而确定滤波增益的最优值。REKF算法的性能在于不确定性模型来表示实际系统，从而达到状态估计误差最小，精度最高。
3) 仿真结果表明，REKF滤波算法可以有效解决量测延时问题，提高姿态估计的精度。

参考文献

[1]	XIONG K, WEI C L, LIU L D. Robust extended Kalman filtering for nonlinear systems with stochastic uncertainties[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part A:Systems and Humans, 2010, 40(2): 399-405. DOI:10.1109/TSMCA.2009.2034836
[2]	XIONG K, WEI C L, LIU L D. Robust Kalman filtering for discrete-time nonlinear systems with parameter uncertainties[J]. Aerospace Science & Technology, 2012, 18(1): 15-24.
[3]	XIONG K, LIU L D, LIU Y. Robust extended Kalman filtering for nonlinear systems with multiplicative noises[J]. Optimal Control Applications & Methods, 2011, 32(1): 47-63.
[4]	REZAEI H, ESFANJANI R M, FARSI M. Robust filtering for uncertain networked systems with randomly delayed and lost measurements[J]. IET Signal Processing, 2015, 9(4): 320-327.
[5]	INOUE R S, TERRA M H, CERRI J P. Extended robust Kalman filter for attitude estimation[J]. IET Control Theory & Applications, 2016, 10(2): 162-172.
[6]	DONG Z, YOU Z. Finite-horizon robust Kalman filtering for uncertain discrete time-varying systems with uncertain-covariance white noises[J]. IEEE Signal Processing Letters, 2006, 13(8): 493-496. DOI:10.1109/LSP.2006.873148
[7]	ZHENG J H, LIU J F. A robust finite-horizon Kalman filter for uncertain discrete time-varying systems with state-delay and missing measurements[J]. International Journal of Grid and Distributed Computing, 2016, 9(3): 229-242.
[8]	WANG F, WANG Z D, LIANG J L, et al. Robust finite-horzion filtering for 2-D systems with randomly varying sensor delays[J]. IEEE Transactions on Systems, Man, and Cybernetics:Ssytems, 2018, 1-13.
[9]	QIN W T, WANG X G, BAI Y L, et al. Arbitrary-step randomly delayed robust filter with application to boost phase tracking[J]. Acta Astronautica, 2018, 145: 304-318. DOI:10.1016/j.actaastro.2018.01.056
[10]	FAN Z, YANG J.A research of gyro/star-sensor integrated attitude determination based on particle filter[C]//Third International Conference on Instrumentation, Measurement, Computer, Communication and Control.Piscataway, NJ: IEEE Press, 2013: 256-261.
[11]	REIF K, GVNTHER S, YAZ E, et al. Stochastic stability of the discrete-time extended Kalman filter[J]. IEEE Transactions on Automatic Control, 1999, 44(4): 714-728.
[12]	XIONG K, LIU L D, ZHANG H Y. Modified unscented Kalman filtering and its application in autonomous satellite navigation[J]. Aerospace Science & Technology, 2009, 13(4): 238-246.
[13]	WANG S, FANG H, TIAN X. Recursive estimation for nonlinear stochastic systems with multi-step transmission delays, multiple packet dropouts and correlated noises[J]. Signal Processing, 2015, 115: 164-175. DOI:10.1016/j.sigpro.2015.03.022
[14]	黄蔚.CKF及鲁棒滤波在飞行器姿态估计中的应用研究[D].哈尔滨: 哈尔滨工程大学, 2015. HUANG W.Application of CKF and robust filter in aircraft attitude estimation[D].Harbin: Harbin Engineering University, 2015(in Chinese).
[15]	XIE L, SOH Y C, DE SOUZA C E. Robust Kalman filtering for uncertain discrete-time systems[J]. IEEE Transactions on Automatic Control, 1994, 39(6): 1310-1314. DOI:10.1109/9.293203