Steinwolf[6-7]提出采用相位调制法来生成平稳的非高斯信号进而模拟路面振动激励,并且通过不断地调整相位值,使仿真信号的峭度达到目标峭度值。Zheng[8]通过响应非高斯信号的PSD来生成平稳的高斯信号,并利用一种改进的“零记忆”非线性转换方法将生成的高斯信号转化为具有指定峭度的非高斯信号。Yu[9]提出了利用散粒噪声来生成具有指定的峭度和PSD的非高斯信号,并实现了通过试验振动台来生成该信号进而应用于可靠性加速实验中。蒋瑜等[10]提出了基于二次相位调制的方法分别生成对称和非对称的超高斯信号,并分析了相位角的变化对偏度和峭度的影响。吴家驹等[11]研究了利用PSD和峭度产生非高斯随机波形的窗函数调制方法,引入了表征平稳的非高斯随机振动的新的参数——跌岩周期,提出了重构非高斯随机振动的新的方法——Beta分布随机数重新排列技术,该方法既可以生成平稳的非高斯信号也可以生成非平稳的非高斯信号;但文中并没有具体探究Beta分布的参数与目标峭度值之间的关系以及该分布的适用范围。徐飞[12]采用幅值调制法(AMT)来仿真生成基于风诱载的非高斯信号,首先构造了服从Weibull的含参分布,然后通过不断迭代寻优的方法使得仿真的调制信号与实际信号随时间变化的均方根值(Root Mean Square, RMS)之间的误差最小,从而确定分布的参数,合成最终的非高斯信号;但文中并没有分析调制信号参数与合成非高斯信号的峭度之间的关系,以及Weibull分布的适用范围,且求解调制参数的过程相对繁琐,误差精度与样本量的大小有很大的关系。
因此,针对现有方法的不足,本文基于窗函数AMT,提出近似模拟的方法分别生成服从Weibull和Beta分布的调制信号,进而合成最终的非高斯信号,并分别分析目标非高斯峭度值与2种分布的参数之间的关系以及2种分布适用范围。
1 非高斯信号的特征描述 一个随机过程可能呈现平稳或非平稳性,高斯或非高斯性。一个各态历经的高斯过程的概率密度函数(PDF)分布为
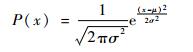 | (1) |
式中:μ为均值;σ为标准差。
广义上讲,幅值不服从高斯分布的随机过程均称为非高斯随机过程,其中既包括具有确定的PDF的随机过程,如指数分布、Weibull分布;又包括没有确定PDF表达式的分布。针对高斯过程,其特性可由PSD完全表征,但是对于非高斯分布,需要采用更高阶统计量即高阶矩和高阶累积量来表征。偏度s和峭度k来定量表征随机过程的非高斯特性。
偏度的计算式为
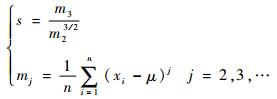 | (2) |
式中:mj为高阶中心矩。
峭度的计算式为
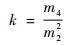 | (3) |
偏度是衡量随机信号偏离对称分布的程度, 偏度不为零的信号必然服从非对称分布。而峭度表征统计频率曲线接近分布中心时的大致状态,其不仅可以区分高斯和非高斯信号,还可以进一步将非高斯信号分为亚高斯和超高斯信号。相对于高斯分布,超高斯分布的随机过程的幅值分布中心区域较窄呈现一个大的峰,并在概率密度曲线上呈现较长的拖尾。而亚高斯分布的随机过程幅值中心区域较窄且比较均匀,但整体的分布区较窄。
信号的另一特性指标为自相关函数(Auto Correlation Function,ACF),自相关函数是信号与延迟后信号之间相似性的一种度量,表征了信号功率随着频率的变化情况,即信号功率在频域的分布状况。其表达式为
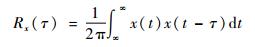 | (4) |
式中:x(t)为时域的信号;τ为延迟量。
相关函数在时间域上描述随机过程的统计特征,而功率谱是在频率域上描述随机过程的统计特征。两者互为一对傅里叶变换对。
2 非高斯随机信号的模拟 针对风诱载以及路面载荷激励等非高斯随机振动信号的模拟,利用窗函数AMT先生成平稳的高斯信号, 然后乘以一个调制信号进而合成最终的非高斯信号, 具体的过程如下。
2.1 实际外场数据的特征分析 分析采集的实际外场数据的特征,获取其统计特征如PSD以及峭度、偏度等信息, 以此判断其是否为非高斯信号。
2.2 平稳高斯信号的模拟 基于快速傅里叶逆变换(IFFT)的原理,Newland[13]利用信号的自功率谱和随机相位来构造幅值,进而生成平稳的零均值的高斯时域信号g(t)为
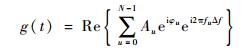 | (5) |
式中:Re{·}表示取实部; Au为幅值, Au=
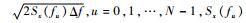
由式(5)可以看出:当N→∞时根据中心极限定理,得到的随机过程近似服从高斯分布,而且它的PSD也接近于所要模拟的目标PSD。因此根据式(1)中外场数据的PSD,生成平稳的高斯时域信号g(t)。
2.3 调制信号的模拟 对于调制信号的生成,Smallwood[14]建议使用Beta分布, 因为该分布只产生正值且灵活性强;而徐飞[12]提出采用Weibull信号作为调制信号,因此分别利用2种分布生成调制信号,研究其参数与目标非高斯信号峭度值之间的关系并探究2种分布的适用范围。由AMT[15]可知:
 | (6) |
式中:w(t)为调制信号;g(t)为高斯信号;G(t)为非高斯信号。
2.3.1 调制信号参数的确定 利用非高斯信号的峭度公式,归一化的非高斯信号、高斯信号的均值都为0,且高斯信号与调制信号相互独立,所以非高斯信号的峭度为
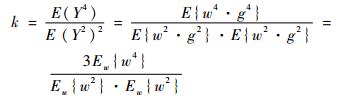 | (7) |
由式(7)可知,目标峭度值与调制信号的参数有关,所以分别探究当调制信号服从Weibull分布和Beta分布时,其参数与目标峭度之间的关系。
1) Beta分布
Beta分布是由区间在[0, 1]的2个正值α,β决定,其高阶原点矩为
 | (8) |
假设目标非高斯信号偏度为0,可得调制信号的偏度值也为0,偏度的计算式为
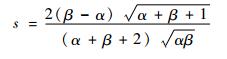 | (9) |
由此可得α=β,代入式(8)可得
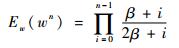 | (10) |
故根据式(7)和式(10)可得非高斯信号的峭度值为
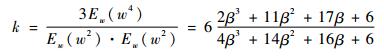 | (11) |
由式(11)可知, 一旦给定了目标峭度值,则Beta分布的参数即可确定。
图 1为目标峭度与参数β之间的关系,由图中可以看出,当峭度值大于6.04时,β为负值,不满足分布要求,因此调制信号参数的合理范围为[0.2,10.2]。当β为[0.2,10.2]时对应的调制信号的PDF如图 2所示,由图中可知,当β>1时,调制信号的PDF符合Beta分布,对应的非高斯信号的峭度值小于5.4;当0.2 < β < 1时,调制信号的PDF分布在两侧,对应的非高斯信号的峭度大于5.4,这是不合理的。因此可以得出结论:
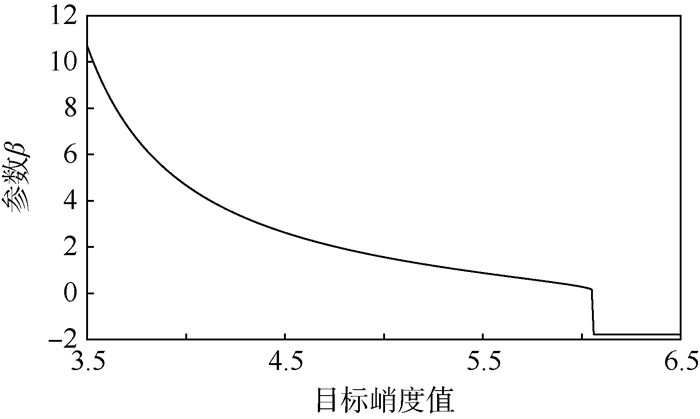 |
| 图 1 目标峭度与参数β的关系 Fig. 1 Relationship between aimed kurtosis and parameter β |
| 图选项 |
 |
| 图 2 参数β为[0.2,10.2]时对应调制信号的PDF Fig. 2 PDF of modulation signal when β is [0.2, 10.2] |
| 图选项 |
当调制信号为Beta分布时,只能够合成目标峭度小于5.4的非高斯信号,对应的合理的参数范围为[1,10.2]。
2) Weibull分布
Weibull分布主要是由形状参数r和比例参数λ的2个正值构成,其高阶原点矩为
 | (12) |
故根据式(7)和式(12)可得非高斯信号的峭度值为
 | (13) |
由式(13)可知,一旦给定了目标峭度值,则Weibull分布的参数r即可确定。
因为仿真非高斯信号与高斯信号具有相同的PSD,即两者具有相同的均方值,则调制信号的均值为1。因此Weibull分布的比例参数λ为
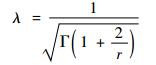 | (14) |
目标峭度值为[3.5,12]时,形状参数r随着峭度的变化如图 3所示。从图中可以看出,随着峭度增加参数r逐渐减小。当峭度小于6.4时,r为负值,这是不合理的,故合理的形状参数r的范围为[1.28,1.88]。形状参数r在[1.28,1.88]时对应的PDF如图 4所示,可以看出其PDF符合Weibull分布,故可得出结论:当调制信号为Weibull分布时,只能够生成目标峭度大于6.4的非高斯信号。
 |
| 图 3 目标峭度与形状参数r的关系 Fig. 3 Relationship between aimed kurtosis and shape parameter r |
| 图选项 |
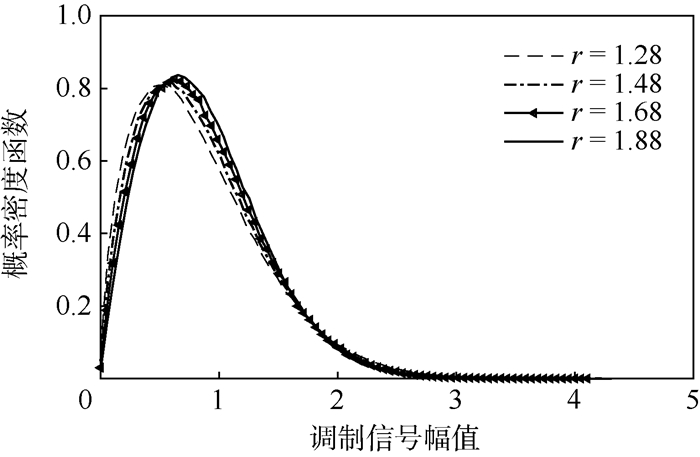 |
| 图 4 形状参数r为[1.28,1.88]时对应调制信号的PDF Fig. 4 PDF of modulation signal when shape parameter r is [1.28, 1.88] |
| 图选项 |
2.3.2 调制信号的近似模拟方法 本文采用一种新的近似模拟的方法用于生成调制信号进而合成最终的非高斯信号。首先根据实测的非高斯信号的幅值趋势生成满足一定分布的随机数个数为N的调制信号,然后利用resample命令进行插值,每个随机点之间的插值数为M个,保证M×N具有与高斯信号相同的长度。
为了确定插值数M,引入了自相关函数来表征。通过实测数据的随时间变化的RMS的自相关函数,即可得到其零穿越时间t,信号的采用频率为fs,故每个随机点之间的插值数M=tfs。
图 5为生成的服从Weibull分布的一个调制信号。假设目标峭度值为8,产生的样本量为N=20,扩增量M=500。
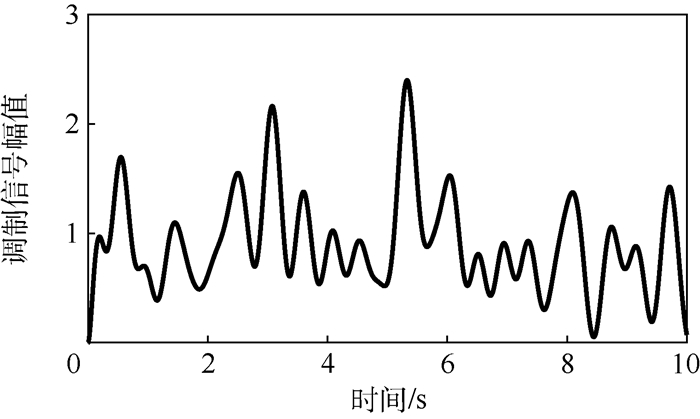 |
| 图 5 服从Weibull分布的调制信号 Fig. 5 Modulation signal following Weibull distribution |
| 图选项 |
2.4 合成非高斯信号 将2.2节中生成的平稳的高斯信号g(t)作为载波信号乘以2.3节中生成的调制信号w(t),生成最终的非高斯信号G(t)。
3 实例分析 3.1 实测数据的特征 通过实际测试得到外场数据,该数据是由安装在一个运动的车辆上的加速度传感器采集得到,通过分析得到实测数据的采样频率为1653Hz, 采样点为160076,峭度值为10.95。实测数据及其随时间变化的均方根值RMS如图 6所示。实测数据的PSD如图 7所示,随时间变化的RMS的自相关函数如图 8所示。由图 7和图 8可以看出,实测信号的RMS相关函数零穿越时间为4s。
 |
| 图 6 实测外场数据和随时间变化的RMS Fig. 6 Measured ourfield data and variation of RMS with time |
| 图选项 |
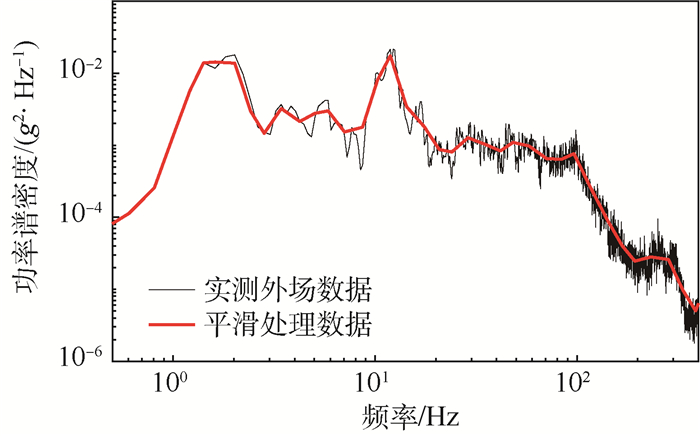 |
| 图 7 实测外场数据和平滑处理数据的PSD Fig. 7 PSD of measured outfield data and smooth data |
| 图选项 |
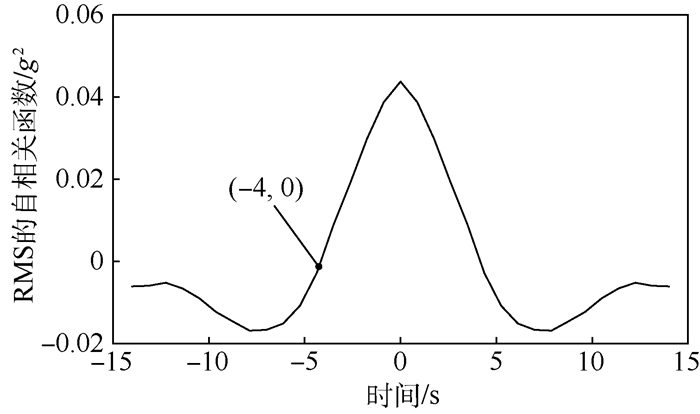 |
| 图 8 实测外场数据RMS的自相关函数 Fig. 8 Auto correlation function of RMS of measured outfield data |
| 图选项 |
3.2 非高斯信号的仿真模拟
3.2.1 高斯信号模拟 因为实测数据的峭度大于3,所以是典型的非高斯信号。根据实测外场数据的PSD采用傅里叶逆变换原理生成稳态的高斯信号如图 9所示。其峭度值为3.01,信号的PSD如图 10所示,由图可以看出产生的高斯信号的PSD与实测外场数据的PSD相同。
 |
| 图 9 仿真的高斯信号 Fig. 9 Simulated Gaussian signal |
| 图选项 |
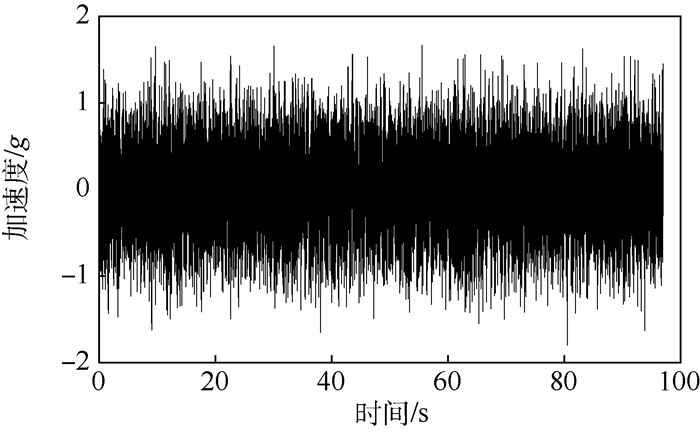 |
| 图 10 实测外场数据和仿真的高斯信号的PSD Fig. 10 PSD of measured outfield data and simulated Gaussian signal |
| 图选项 |
3.2.2 调制信号模拟 根据实测外场数据的峭度值为10.95,其峭度值大于6.4,所以可以采用Weibull分布生成调制信号,由式(13)和式(14)可以得到Weibull分布的参数为:r=1.2779, λ=0.8473。为了构造调制信号,根据实测外场数据RMS的自相关函数的零穿越时间为4s,采样频率fs=1653Hz,故采样间隔点数为6612,根据采用点数一般为1024的整数倍,所以插值数M=8192,根据总的采样点数,可以确定生成的调制信号如图 11所示,仿真的自相关函数和实测外场数据RMS的自相关函数如图 12所示,从图中可以看出两者的自相关函数的零穿越时间很接近,说明仿真的调制信号满足要求。
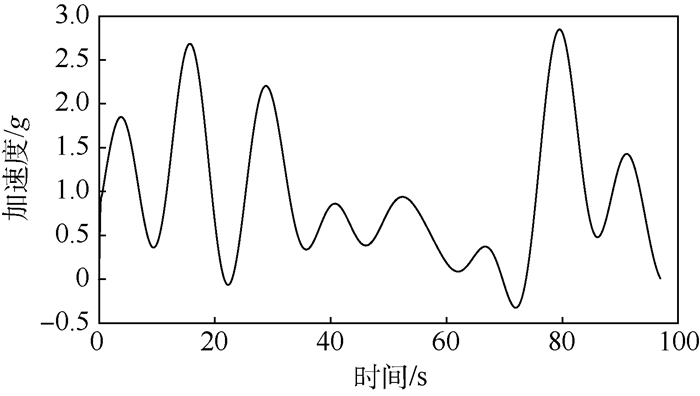 |
| 图 11 仿真的调制信号 Fig. 11 Simulated modulating signal |
| 图选项 |
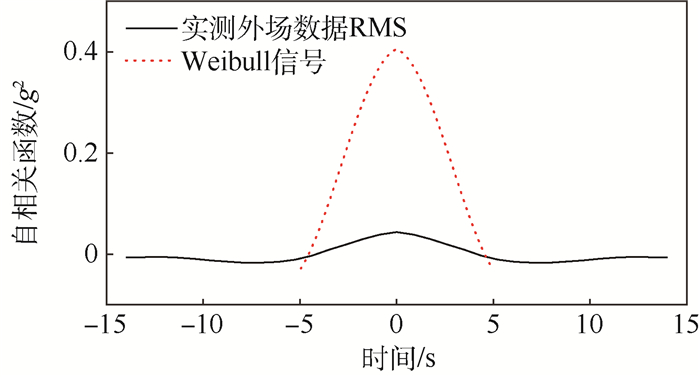 |
| 图 12 实测外场数据RMS和Weibull信号的自相关函数 Fig. 12 Auto correlation function of measured outfield data RMS and Weibull signal |
| 图选项 |
3.2.3 仿真的非高斯信号 根据生成的高斯信号和调制信号,利用AMT将两者相乘得到最终的非高斯信号。由此产生的非高斯信号如图 13所示,其峭度值为11.12,与外场数据的峭度值相近。图 14为仿真的非高斯信号的PSD和实测外场数据的PSD,图 15为仿真信号的PDF和实测外场数据的PDF,由图可以看出两者的PSD和PDF很接近,说明方法的准确性。
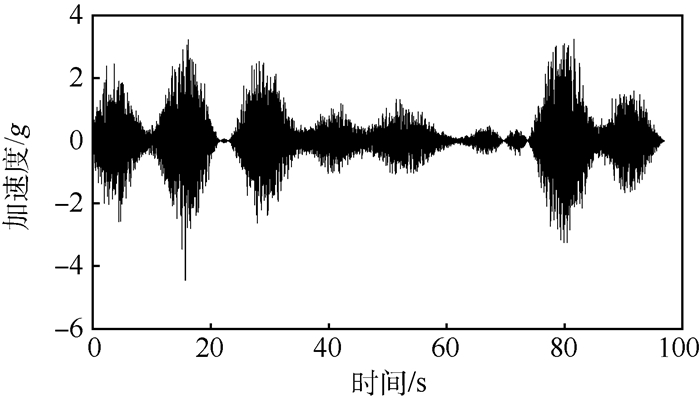 |
| 图 13 仿真的非高斯信号 Fig. 13 Simulated non-Gaussian signal |
| 图选项 |
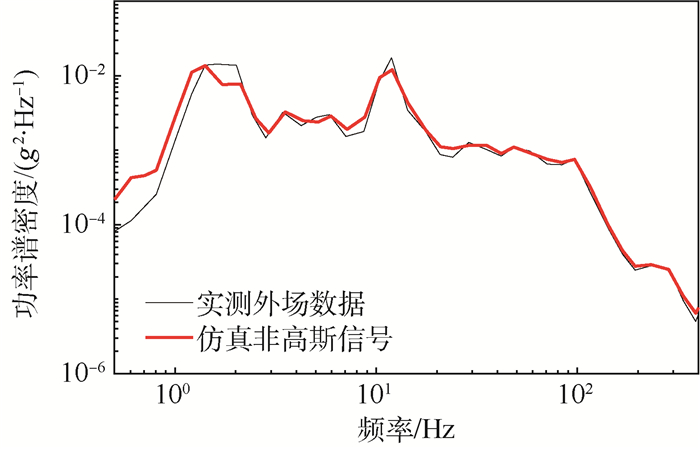 |
| 图 14 实测外场数据和仿真非高斯信号的PSD Fig. 14 PSD of measured outfield data and simulated non-Gaussian signal |
| 图选项 |
 |
| 图 15 不同信号的概率密度函数 Fig. 15 PDF of different signals |
| 图选项 |
4 结论 1) 提出利用AMT生成非高斯信号的方法,通过案例得到仿真的信号具有与实测信号相同的PSD、PDF和峭度,说明了本文方法的正确性。
2) 对于调制信号,采用近似模拟生成的方法,分别利用Weibull分布和Beta分布生成调制信号,研究分析了分布参数与目标峭度之间的关系。
3) 分别探究Weibull分布和Beta分布适合生成非高斯信号峭度值的范围,分析可知Weibull分布只适合于生成峭度大于6.4的非高斯信号,而Beta分布只适合于生成峭度小于5.4的非高斯信号。
参考文献
| [1] | BENDAT S, PIERSOL G.Random data: Analysis and measurement procedures[M]. 4th ed.Los Angeles: John Wiley and Sons, Inc., 2010: 1799-1806. |
| [2] | VINCENT R.On the non-Gaussian nature of random vehicle vibration[C]//Proceedings of the World Congress on Engineering, 2017, 2: 1219-1224. |
| [3] | KNANI K B. Fatigue damage assessment of a car body-in-white using a frequency-domain approach[J]. International Journal of Materials & Products Technology, 2007, 30(1): 172-198. |
| [4] | ZAKHAROV V E, DYACHENKO A I, PROKOFIEV A O. Freak waves as non-linear stage of Stokes wave modulation instability[J]. European Journal of Mechanics, 2006, 25(5): 677-692. DOI:10.1016/j.euromechflu.2006.03.004 |
| [5] | YI H, BO L. Non-stationary and non-Gaussian characteristics of wind speeds[J]. Wind and Structures, 2017, 24(1): 59-78. DOI:10.12989/was.2017.24.1.059 |
| [6] | STEINWOLF A. Closed-loop shaker simulation of non-Gaussian random vibration.Part 1:Discussion and methods[J]. Test Engineering and Management, 2006, 68(3): 10-13. |
| [7] | STEINWOLF A. Closed-loop shaker simulation of non-Gaussian random vibration.Part 2:Numerical and experimental results[J]. Test Engineering and Management, 2006, 68(5): 14-19. |
| [8] | ZHENG R H. Control method for multi-input multi-output non-Gaussian random vibration test with cross spectra consideration[J]. Chinese Journal of Aeronautics, 2017, 30(6): 1895-1906. DOI:10.1016/j.cja.2017.10.001 |
| [9] | YU Y Y. Generation of non-Gaussian random vibration excitation signal for reliability enhancement test[J]. Chinese Journal of Aeronautics, 2007, 20(3): 236-239. DOI:10.1016/S1000-9361(07)60038-7 |
| [10] | 蒋瑜, 陶俊勇, 王得志, 等. 一种新的非高斯随机振动数值模拟方法[J]. 振动与冲击, 2012, 31(19): 169-173. JIANG Y, TAO J Y, WANG D Z, et al. A novel approach for numerical simulation of a non-Gaussian random vibration[J]. Journal of Vibration and Shock, 2012, 31(9): 169-173. (in Chinese) |
| [11] | 吴家驹, 付玮, 张鹏飞, 等. 基于β分布随机数排序的非高斯振动模拟方法[J]. 强度与环境, 2017, 44(2): 10-17. WU J J, FU W, ZHANG P F, et al. Simulation method of non-Gaussian vibration base on re-arrangement of β distribution random number[J]. Structure & Environment Engineering, 2017, 44(2): 10-17. (in Chinese) |
| [12] | XU F. On the shaker simulation of wind-induced non-Gaussian random vibration[J]. Shock and Vibration, 2016, 2016(6): 1-10. |
| [13] | NEWLAND D E.An introduction to random vibrations and spectral analysis[M]. 2nd ed.New York: Longman Inc., 1984: 1102-1203. |
| [14] | SMALLWOOD D O. Vibration with non-Gaussian noise[J]. Journal of the Institute of Environmental Science and Technology, 2009, 52(3): 13-20. |
| [15] | RIZZI S A, PRZEKOP A, TURNER T L.On the response of a nonlinear structure to high kurtosis non-Gaussian random loadings[C]//The 8th International Conference on Structural Dynamics, 2011: 2697-2704. |
