作为飞机级HIRF试验的重要内容,低电平扫描场(Low Level Swept Field, LLSF)具有测试便捷、降低待测飞机潜在风险等优点[2]。LLSF测试是采用外部电磁波照射飞机舱室,接收天线或场强探头置于舱室内测试内部场强,通过与校准值对比获得飞机舱室的衰减特性。测试过程中由于舱室存在驻波,舱室内不同位置场强变化较大,通常需要在舱室内安装足够多的接收天线/探头,或者采用有限个接收天线在不同位置开展多次测试, 寻找舱室内场强最大值[3-4],这种方法耗时耗力。参考混响室设计方法,通过内置搅拌器,改变边界条件,使得在搅拌器的一个旋转周期内接收天线/探头位置出现场强最大值,实现场统计均匀,达到最大值快速获取的目的[5-7]。不同于混响室,飞机舱室通常是非封闭结构,存在的门窗、导流孔等开口将影响到舱室内的局部能量密度和总场均匀性[8-9],而且,目前的文献仅对发射天线置于混响室内部的情况进行分析,还没有开展外部电磁波照射下非封闭舱室内场统计均匀分析。
本文重点对LLSF测试中非封闭飞机舱室内的场统计均匀测试方法展开研究,通过建立方形舱室内置搅拌器的仿真及试验系统,验证了非封闭舱室内产生统计均匀电场的可行性;结合舱室和搅拌器的仿真模型,提出了基于遍历和递归算法的场均匀区域检验方法。获取的方形舱室和圆柱舱室内有限场均匀区域的规律,可为实际飞机级LLSF试验过程中数据采集提供重要指导。
1 场均匀性判定方法 舱室内通过放置旋转的搅拌叶片,在较大空间内获得具有统计特性的均匀场。在这个均匀场区,搅拌器完成一个周期的所有步进过程后,区域内任一点处的电磁场强都可以达到相同的最大场强值。LLSF测试过程中,由于舱室非封闭开口的存在,搅拌器的均匀区域不同于混响室的均匀场区域,与搅拌器大小、舱室开口大小、频率等有关。按照IEC 61000-4-21标准[10],均匀性采用如下的判定方法。
通过选取区域所在的8个顶点作为接收探头位置,将8个位置的最大场强值归一化到平均输入功率的平方根:
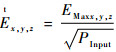 | (1) |
式中:EMaxx, y, z为每个探头x、y、z轴分量的最大测量值;
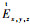
针对每个频率,计算接收探头每个轴向的测量值的最大归一化平均值:
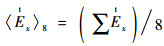 | (2) |
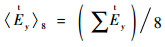 | (3) |
 | (4) |
设定每个轴向具有同样权重,计算接收探头所有测量值的最大归一化平均值

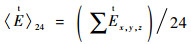 | (5) |
式中:〈〉表示算术平均值。
搅拌器旋转一周,以8个位置中每个位置得到的最大平均值的标准偏差来确定场均匀性,用接收探头每个轴向的单独数据和总数据集来计算标准偏差。
标准偏差计算式为
 | (6) |
式中:
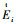

用与平均值有关的分贝(dB)数表示标准偏差:
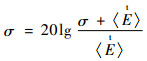 | (7) |
如果所有场向量的标准偏差不超过规定的标准偏差值,则认为满足了场均匀性要求。
2 非封闭舱室内场均匀性 为了获取飞机非封闭舱室内场统计均匀特性,针对飞机不同类型舱室的几何形状,分别选取方形舱室和圆柱舱室作为研究对象开展仿真与试验分析。其中方形舱室用于起落架舱等的特性研究,圆柱舱室可用于研究飞机客舱、驾驶舱等内部的场均匀性。
2.1 方形舱室试验 制作了金属方形舱室和内置搅拌器,用于电场均匀性试验。方形舱室的长宽高分别为:l=2 m,w=1 m,h=1 m,舱室左右两侧分别有5个0.15 m×0.1 m的窗口,舱室前侧有一个0.3 m×0.4 m的开口,孔隙率(窗口面积与舱室面积的比值)为2.7%。搅拌叶片由2个0.3 m×0.3 m正方形铝板折叠后拼接,叶片下方为驱动盒和转轴,搅拌叶片拼接后的对角尺寸约为0.8 m,大于舱室宽度的3/4。方形舱室和搅拌器的坐标关系如图 1所示,坐标原点位于转轴顶部中心。
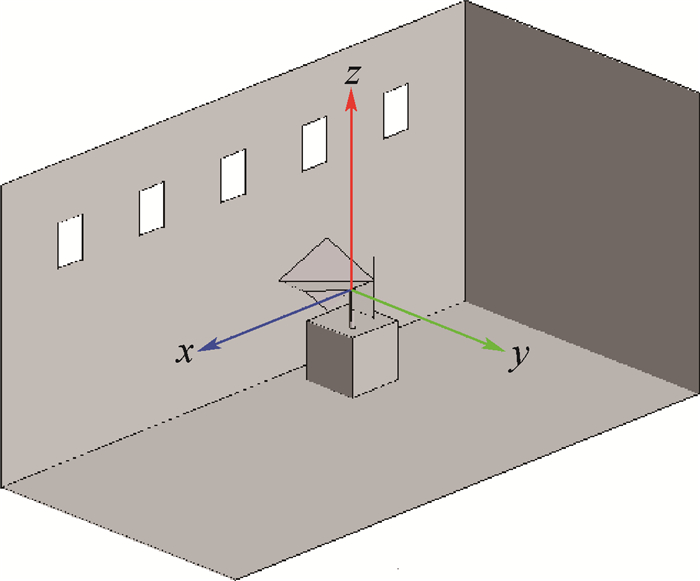 |
| 图 1 直角坐标系中方形舱室与搅拌器位置 Fig. 1 Location of cuboid-shaped cabin and stirrer under rectangular coordinate system |
| 图选项 |
方形舱室的谐振频率和模式数目分别通过式(8)和式(9)进行计算[11-12]:
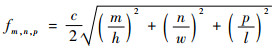 | (8) |
 | (9) |
式中:c为光速;l、w、h分别为舱室的长、宽、高,m;m、n、p为0或整数;f为频率,Hz。
一般条件下,混响室最低可用频率(Lowest Usable Frequency, LUF)必须大于舱室的最低谐振频率f011的3倍,同时MIL-STD-461E标准[13]要求,在LUF下至少存在100个模。根据式(8)和式(9)的计算,此舱室LUF约为510 MHz。
试验频率范围为400 MHz~1 GHz,搅拌叶片的最大旋转区域与舱室内壁的间距至少为λ/4,根据最低仿真频率400 MHz,此间距设置为0.2 m,同时,单片搅拌叶片尺寸大于λ/4, λ为波长。数据采集区域A为:x∈(0.45,0.75) m,y∈(-0.25,0.25) m,z∈(-0.25,0.25) m。
场均匀性试验布置如图 2所示,发射天线于舱室外10 m处,发射垂直极化的电磁信号作用于方形舱室,舱室待测区域内采用光纤连接的场强探头进行数据采集。测试过程为软件自动化控制,搅拌器叶片以15°步进旋转,每一个步进下获取待测频段内x、y和z轴场强的最大值。
 |
| 图 2 场均匀性试验布置 Fig. 2 Field uniformity test layout |
| 图选项 |
根据IEC 61000-4-21标准[10]中混响室设计时测试区域的场均匀性判定方法,舱室内部待测区域的场均匀性标准偏差需达到的指标要求如表 1所示。
表 1 场均匀性要求的标准偏差[10] Table 1 Allowable standard deviation for field uniformity [10]
| 频率/MHz | 场均匀性标准偏差 |
| 100~400 | 由100MHz频率的4dB线性递减至400MHz的3dB |
| 400以上 | 3dB |
表选项
采用均匀性判定方法,区域A的场均匀性结果如图 3所示,图中σx、σy和σz分别为x、y、z轴分量的标准偏差。可以看出,在550 MHz~1 GHz范围内,总场强值以及x、y、z轴分量的均匀性均满足3 dB指标要求。试验验证了非封闭舱室在外部电磁波照射下仍具有较好的均匀场特性,并且随着频率的升高,均匀性越好。
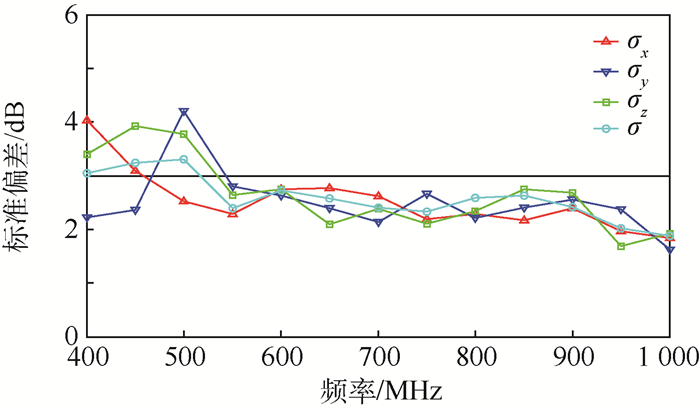 |
| 图 3 方形舱室待测区域场均匀性测试结果 Fig. 3 Field uniformity test results in testing region of cuboid-shaped cabin |
| 图选项 |
采用开口切割和铝箔敷贴的方式,将舱室前侧开口和两侧窗口的形状由矩形更改为圆形,孔隙率不变的情况下,采用同样的试验方法获取待测区域内的场均匀性,结果如图 4所示。可以看出,在开口横向或纵向等任一维度不发生较大变更的情况下,开口的形状对待测区域的场均匀性影响不大。
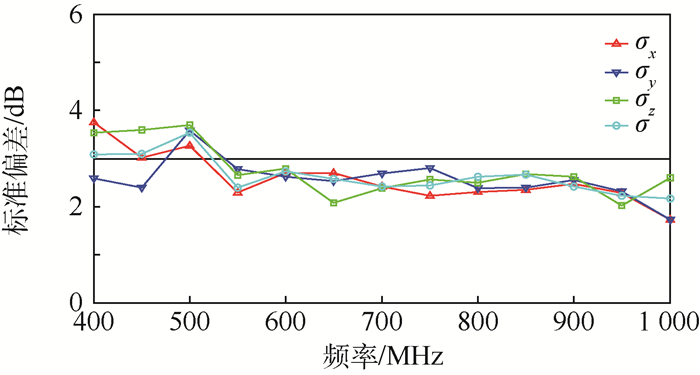 |
| 图 4 方形舱室圆形开口下待测区域场均匀性测试结果 Fig. 4 Field uniformity test results in testing region of cuboid-shaped cabin with circular apertures |
| 图选项 |
分别将舱室前侧及左右两侧窗口的现有开口扩至0.6 m×0.8 m和0.3 m×0.2 m的矩形,孔隙率由2.7%增加为10.8%。采用上述方法,在方形舱待测区域内进行数据采集,并得到待测区域内的场均匀性测试结果,如图 5所示。可以看出,在一定程度上增大非封闭舱室的孔隙率,舱室内待测区域的场均匀性有变差的趋势。
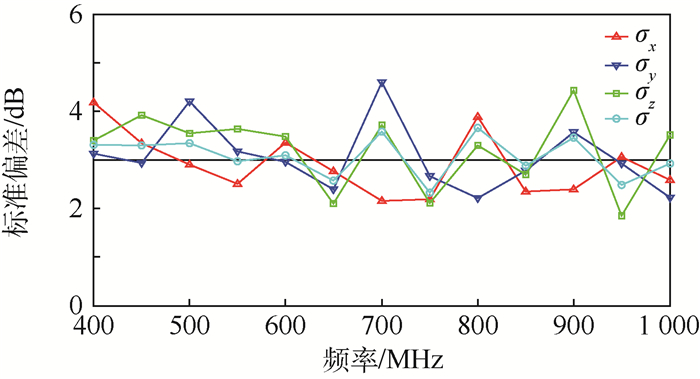 |
| 图 5 方形舱室空隙率变大后待测区域场均匀性测试结果 Fig. 5 Field uniformity test results in testing region of cuboid-shaped cabin for increased aperture ratio |
| 图选项 |
2.2 方形舱室建模与仿真 为了进一步分析非封闭舱体在LLSF下的电场均匀性及其特点,建立了与测试配置一致的方形舱室仿真模型,如图 6所示。考虑到选取的数值软件能够实现舱室内多次反射、损耗的精确计算,同时可方便控制搅拌器叶片旋转的状态,本文选用全波数值仿真软件FEKO进行求解。外部电磁波以垂直极化方式分别从x轴方向(φ=0°)以及y轴方向(φ=90°)进行照射。搅拌叶片的最大旋转区域距离舱室内壁有λ/4的长度,根据最低仿真频率400 MHz,距离设置为0.2 m。待分析的均匀区域A与测试选取的区域一致。
 |
| 图 6 方形舱室内部场均匀性仿真模型 Fig. 6 Simulation model for field uniformity in cuboid-shaped cabin |
| 图选项 |
图 7为仿真和测试手段分别计算得到的总数据集标准偏差的对比结果。可以看出,仿真数据与测试数据较为一致,验证了仿真方法可用于分析均匀场区域的有效性。在LUF以上的550 MHz~ 1 GHz频段范围内,场均匀性计算结果均在3 dB以内。
 |
| 图 7 仿真与测试总数据集场均匀性标准偏差对比 Fig. 7 Comparison of simulated and test standard deviations of field uniformity for all vectors |
| 图选项 |
2.3 圆柱舱室建模与仿真 飞机舱室以圆柱形结构居多,建立了非封闭圆柱舱室的仿真模型,如图 8所示。圆柱舱室的截面半径为0.5 m,长度为2 m,在舱室左右两侧分别有3个约0.08 m×0.2 m的窗口,舱室前侧有一个0.72 m×0.32 m的开口,孔隙率约为4.2%。搅拌器模型与方形舱室中所用模型一致,待分析的均匀区域B与方形舱室一致。
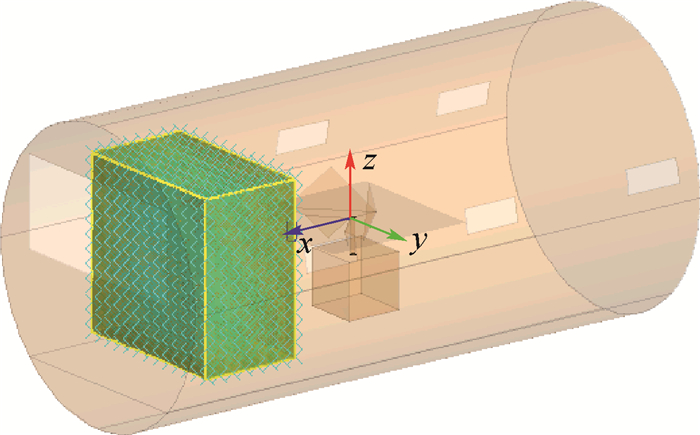 |
| 图 8 圆柱舱室内部场均匀性仿真模型 Fig. 8 Simulation model for field uniformity in cylindrical cabin |
| 图选项 |
圆柱舱室的谐振频率和模式数目可分别通过式(10)和式(11)进行计算[14]:
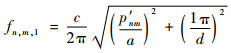 | (10) |
 | (11) |
式中:a和d分别为半径和长度,m;p′nm为贝塞尔函数的求解根,其值通过查询数据表给出;r为半径。
在400 MHz~1 GHz频率范围,外部电磁波以垂直极化方式从φ=0°和φ=90°方向进行照射,仿真得到区域B的8个顶点在搅拌器旋转过程x、y和z轴的电场强度值。根据判定方法,计算得到圆柱舱室在该区域的场均匀性,如图 9所示。
 |
| 图 9 圆柱舱室照射下的场均匀性标准偏差 Fig. 9 Standard deviations of field uniformity in cylindrical cabin illumination |
| 图选项 |
由图 9可以看出,550 MHz~1 GHz频段范围,区域B的场均匀性满足要求。通过调整圆柱舱室两侧6个窗口的大小,分析了不同孔隙率下在x分量电场均匀性的标准偏差(y和z分量的结果类似),如图 10所示。结果表明,在孔隙率小于8%的情况下,孔隙开口并不影响舱室内区域B的场均匀性。
 |
| 图 10 不同孔隙率下x分量电场的标准偏差 Fig. 10 Standard deviations for x vector electric field with different aperture ratios |
| 图选项 |
3 场均匀区域检验方法 实际飞机级LLSF测试过程中,飞机的各个舱室变化差异大且空间狭小不规则,无法制作传统混响室内要求的搅拌器,只能通过制作足够大尺寸的搅拌叶片。单一搅拌叶片尺寸至少大于最小分析频率下的λ/4,拼接后的搅拌器最大长度要求满足舱室任一维边长的3/4。
寻找满足分析频带内均匀性要求的区域作为接头天线/探头的位置。实际上,在场均匀性不满足场均匀性要求的较低频段(LUF附近),搅拌叶片附近仍存在较小的均匀场区域。通过方形舱室和圆柱舱室的仿真数据分析,给出了2类舱室内的均匀区域体积随频率变化的关系,如图 11所示。为了有效解决飞机LLSF测试数据采集难的问题,本文提出了基于遍历和递归算法的场均匀区域检验方法。
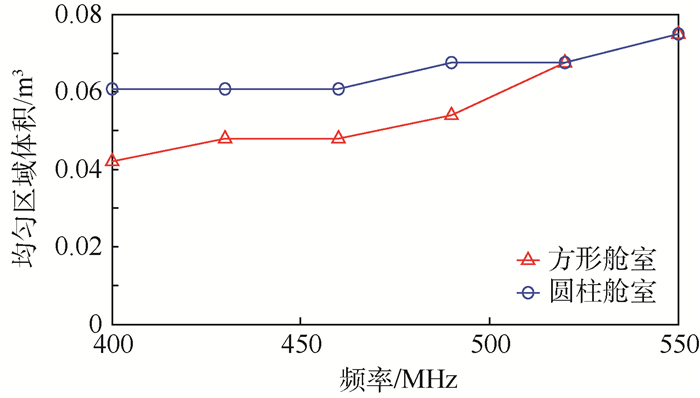 |
| 图 11 均匀区域体积随频率变化 Fig. 11 Variation of uniform region volume with frequency |
| 图选项 |
以方形舱室为例,基于递归算法,在区域A内采用遍历的方式进行查找,如图 12所示。对区域A内的每个子区域进行检索和验证,得到满足均匀要求的子区域并记录,形成不同频率下的子区域矩阵 f1(D11,D21,D31,…)、f2(D12,D22,D32,…)等。最后,将所有频率下获取的子区域进行递归比对筛选,得到可用于LLSF试验的目标子区域[15-16]。
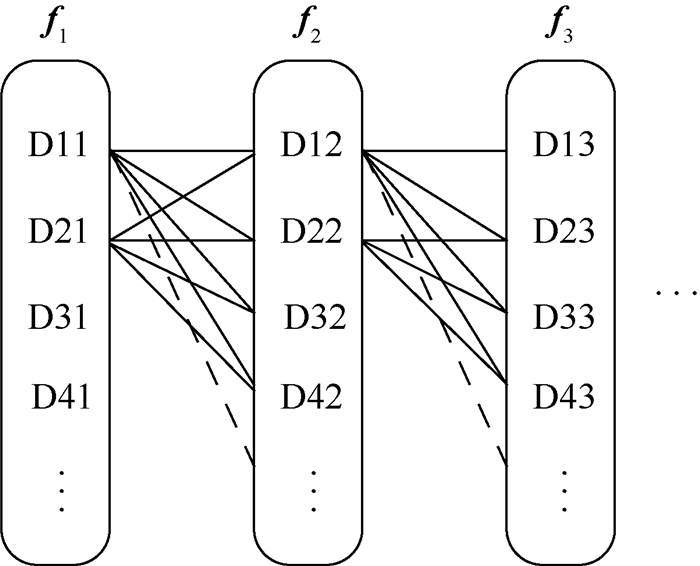 |
| 图 12 遍历查找检验方法 Fig. 12 Schematic diagram of traversal searching and testing method |
| 图选项 |
图 13是通过对方形舱室的区域A进行查找检验后得到的均匀区域A′的标准偏差,均匀区域A′的坐标范围为:x∈(0.45,0.75) m,y∈(-0.15,0.15) m,z∈(-0.15,0.25) m,在400 MHz~1 GHz范围内符合均匀性要求。
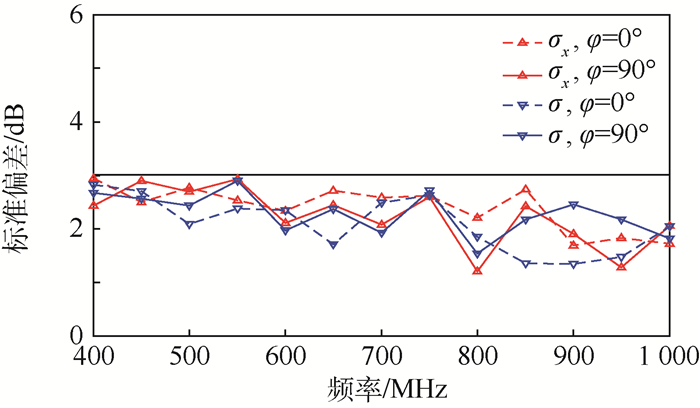 |
| 图 13 方形舱室区域A′的场均匀性标准偏差 Fig. 13 Standard deviations of field uniformity in region A′of cuboid-shaped cabin |
| 图选项 |
同样地,采用上述递归算法在圆柱舱室区域B内查找。最终得到的均匀区域为B′,坐标范围为:x∈(0.45,0.75) m,y∈(-0.25,0.2) m,z∈(-0.25,0.2) m,标准偏差如图 14所示。选取的区域能够用于指导LLSF测试时接收探头的空间布置。
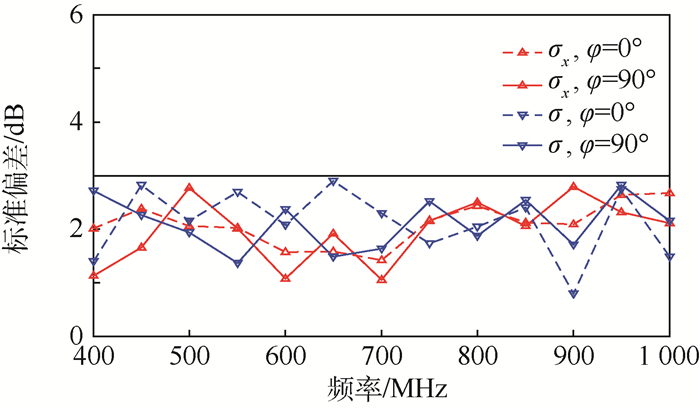 |
| 图 14 圆柱舱室区域B′的场均匀性标准偏差 Fig. 14 Standard deviations of field uniformity in region B′of cylindrical cabin |
| 图选项 |
4 结论 本文主要解决飞机级LLSF测试过程中非封闭舱室内场均匀性的可行性以及区域检验问题。
1) 通过测试和仿真验证了外部电磁波照射下,在非封闭舱室内置相当尺寸的搅拌叶片,仍可有效得到待测区域的场均匀特性。只需单一搅拌叶片的尺寸大于最小频率下λ/4,拼接后的搅拌器最大长度为舱室任一维边长的3/4,舱室孔隙率通舱在8%以内。
2) 随着频率的升高,搅拌器的搅拌性能越好。对于不满足均匀性要求的频率范围,在一定的孔隙和搅拌叶片尺寸下,提出了基于遍历和递归算法的场均匀区域检验方法,获取了模式搅拌工作下的非封闭舱室内的有限均匀区域。
3) 方形舱室和圆柱舱室的场均匀性结果对比表明,舱室内部的场均匀特性存在相似性,均匀场区域检验方法可推广应用于其他类型结构舱体。
参考文献
| [1] | RASEK G A, SCHRODER A, TOBOLA P, et al. HIRF transfer function observations:Notes on results versus requirements and certification approach[J]. IEEE Transactions on Electromagnetic Compatibility, 2015, 57(2): 195-202. DOI:10.1109/TEMC.2014.2381095 |
| [2] | 胡平道. 低电平耦合技术在飞机级试验中的应用[J]. 微波学报, 2010(s2): 58-61. HU P D. LLC approach using in aircraft test[J]. Journal of Microwaves, 2010(s2): 58-61. (in Chinese) |
| [3] | HATFIELD M O, PLUIM W P, PRICE W.Investigation into in-situ shielding effectiveness testing of transport aircraft[C]//2003 IEEE Symposium on Electromagnetic Compatibility.Piscataway, NJ: IEEE Press, 2003: 414-418. https://ieeexplore.ieee.org/document/1236632 |
| [4] | TAVERNES F, LAISNE A, NOUVEL M, et al.On the use of the Hatfield technique for EM qualification of large aircrafts[C]//Electromagn Compatibility Europe Workshop, 2007. |
| [5] | Defence Procurement Agency.Electromagnetic compatibility part 4 platform and system test and trials: 51-59[S].Glasgow: Ministry of Defence, 2010: 51-59. |
| [6] | MAARLEVELD M, HIRSCH H.Experimental investigation on electronic mode stirring in small reverberation chambers by frequency modulated signals[C]//EMC Europe 2011, 2011: 26-30. https://ieeexplore.ieee.org/document/6078591 |
| [7] | 徐鑫, 魏明, 程二威, 等. 频率搅拌混响室内小屏蔽体的场均匀性检验[J]. 军械工程学院学报, 2013, 25(6): 44-48. XU X, WEI M, CHENG E W, et al. Field uniformity test of small enclosures in frequency stirring reverberatio chamber[J]. Journal of Ordnance Engineering College, 2013, 25(6): 44-48. DOI:10.3969/j.issn.1008-2956.2013.06.009 (in Chinese) |
| [8] | 陈亮, 余志勇, 滕向如, 等. 通风孔对混响室场均匀性的影响[J]. 科学技术与工程, 2015, 15(34): 1-6. CHEN L, YU Z Y, TENG X R, et al. Influence of vents on field uniformity of reverberation chamber[J]. Science Technology and Engineering, 2015, 15(34): 1-6. DOI:10.3969/j.issn.1671-1815.2015.34.001 (in Chinese) |
| [9] | ANDRIEU G, TRISTANT F, REINEIX A. Investigations about the use of aeronautical metallic halls containing apertures as mode-stirred reverberation chambers[J]. IEEE Transactions on Electromagnetic Compatibility, 2013, 55(1): 13-20. DOI:10.1109/TEMC.2012.2202240 |
| [10] | IEC Central Office.Electromagnetic compatibility (EMC): Part 4-21: Testing and measurement techniques reverbera-tionchamber test methods: IEC 61000-4-21[S].Switzerland: International Electro Techniacal Commission, 2011: 41-45. |
| [11] | 王淞宇.异型混响室的设计与仿真[D].北京: 北京交通大学, 2012: 8-10. WANG S Y.Design and simulation of reverberation chamber with irregular shape[D].Beijing: Beijing Jiaotong University, 2012: 8-10(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10004-1012318869.htm |
| [12] | 丁坚进.混响室的理论、设计和测试[D].北京: 北京交通大学, 2007: 23-25 (in Chinese).DING J J.Theory, measurement and design of reverberation chamber[D].Beijing: Beijing Jiaotong University, 2007: 23-25(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10004-2007036701.htm |
| [13] | Department of Defense Interface Standard.Requirements for the control of electromagnetic interference emissions and susceptibility: MIL-STD-461E[S].Washington, D.C.: Department of Defense, 1999: 122-123. |
| [14] | POZAR D M.微波工程[M].张肇仪, 周乐柱, 吴德明, 译.北京: 电子工业出版社, 2011: 242-247. POZAR D M.Microwave engineering[M].ZHANG Z Y, ZHOU L Z, WU D M, translated.Beijing: Electronics Industry Press, 2011: 242-247(in Chinese). |
| [15] | 尹帮治. 二叉树遍历的通用递归算法研究与实现[J]. 电脑知识与技术, 2008, 3(19): 132-134. YIN B Z. Research and realization of the general recursive algorithm of traversing binary tree[J]. Computer Knowledge and Technology, 2008, 3(19): 132-134. DOI:10.3969/j.issn.1009-3044.2008.19.056 (in Chinese) |
| [16] | 胡慧泽.基于分步查找的高效复合模式查找算法[D].西安: 西安电子科技大学, 2010: 13-20. HU H Z.Efficient composite pattern finding algorithm based on asynchronous finding[D].Xi'an: Xidian University, 2010: 13-20(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10701-1011076809.htm |
