对于中国液体型号火箭而言，推进剂的质量可以占到火箭起飞质量的90%左右。推进剂贮箱作为运载火箭的重要构件，其作用不只是用来盛贮推进剂，同时也是不可或缺的承力构件^[1]。因此，推进剂贮箱的可靠性是制约航天发射成败、影响航天发射安全的重要因素。
推进剂贮箱作为大型焊接结构，其焊接接头由于气孔、裂纹、软化与变形等原因，真实应力强度难以确定，是贮箱应力强度不确定性的主要来源^[2]。而且贮箱在进行长储试验的过程中，地震响应^[3]、应变裂纹^[4-5]等不确定因素，都对贮箱应力强度分析及可靠性评估提出了巨大的挑战。在传统的可靠性方法中，通常应用概率论和模糊理论处理不确定性问题。但概率可靠性和模糊可靠性模型均需要大量精确的原始数据作为基础，用于定义参数的概率分布或隶属函数。而在贮箱的实际应用过程中这些要求很难得到满足，因此在各种不同概率分布和可能性分布的假设下，得出的可靠状态往往有很大差异。
20世纪90年代，Ben-Haim首次提出不确定凸集模型理论，并将其引入到薄壁壳体的稳定性分析中^[6-7]，为有效处理结构的不确定性问题提供了新方法。Elishakoff和Ben-Haim针对结构初始缺陷的不确定性问题，对圆柱薄壳的凸模型可靠性进行了研究^[8]。邱志平、胡永明^[9]和王晓军^[10]应用区间分析与凸模型理论，对不确定几何缺陷杆件的动态屈曲问题进行了研究，探讨了初始缺陷对结构可靠性及屈曲状态的严重影响。Wang等将凸模型理论与传统的概率理论与模糊集合理论进行了对比分析^[11]，证明了凸模型理论处理不确定性问题的优越性。Jiang等分别针对线性及非线性凸模型不确定性问题，确定了FOAM与SOAM近似方法^[12]，其中FOAM仅能处理线性问题，而SOAM方法由于存在Hessian矩阵，运算困难。Guo和Lu针对工程系统中的有界不确定性问题，提出了一种通用的非概率可靠性方法^[13]，其主要是针对系统的可靠性测试数据进行分析。Courtois和Denuit对凸模型可靠性临界状态函数边界值确定方法的研究^[14]，以及Karuna和Monohar结合概率与超椭球非概率模型来处理结构不确定性问题的研究^[15]，均为不确定条件下贮箱应力强度可靠性的评估提供了参考。
本文将区间凸模型理论引入不确定条件下贮箱的可靠性评估中，在推导分析推进剂贮箱应力分布的基础上，将贮箱等效应力与临界应力的不确定性转换为区间凸集的形式，结合应力强度干涉理论及正则化区间面积比方法，提出了推进剂贮箱应力强度区间凸模型可靠性评估方法。
1 贮箱应力分析 目前，椭球底圆柱贮箱是中国运载火箭应用的主要贮箱类型。为确定贮箱各部分的应力分布及等效应力区间凸集，在贮箱椭球下底、上底及圆柱筒数学模型的基础上，对贮箱的经向应力与环向应力进行推导分析。
1.1 贮箱椭球下底应力 椭球下底主要承受贮箱内部增压、推进剂液压及参考面以下推进剂重力的作用。根据椭球下底的受力情况，建立贮箱椭球下底数学模型^[16]，如图 1所示。图中：δ_b为椭球下底壁厚；R为贮箱半径；a为椭球母线长半轴；b为椭球母线短半轴；r为中心轴到参考点距离；R₁为第一曲率半径；R₂为第二曲率半径；φ_b为R₂与中心轴y_b的夹角。

图 1 贮箱椭球下底模型[16] Fig. 1 Ellipsoid bottom model of tank[16]

图选项

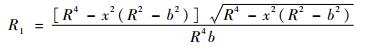(1)

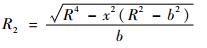(2)

(3)

设贮箱椭球下底母线的椭圆方程为

(4)

贮箱椭球下底参考面NN上的平衡方程为

(5)

式中：ΔP为内部增压；σ_b1为椭球下底经向应力；n为轴向过载系数；g为重力加速度；ρ为推进剂密度；h_b为椭球下底参考面液面高度；V_b为参考面以下的容积，定义为

(6)

在NN参考面上，联立式(5)和式(6)，求得σ_b1为

(7)

贮箱椭球下底模数m定义为m=a/b=R/b。联立式(1)~式(4)，可得

(8)

则式(7)可表示为

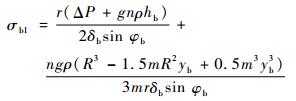(9)

根据无矩理论，可得贮箱椭球下底任意微元的平衡方程为

(10)

式中：σ_b2为椭球下底环向应力。
联立式(8)、式(9)与式(10)，可得椭球下底环向应力为

(11)

1.2 贮箱椭球上底应力 贮箱椭球上底与椭球下底结构相同，但仅受内部增压的作用。根据贮箱椭球上底的应力情况，建立贮箱椭球上底数学模型，如图 2所示。

图 2 贮箱椭球上底模型 Fig. 2 Ellipsoid roof model of tank

图选项

图中：δ_r为椭球上底壁厚；φ_r为R₂与中心轴y_r的夹角。则从MM参考面上的平衡方程为

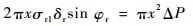(12)

将x=r=R₂sin φ_r代入式(12)，且存在

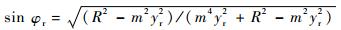(13)

则可得椭球上底经向应力为

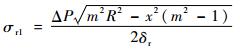(14)

根据平衡方程

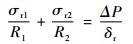(15)

可得椭球上底环向应力为

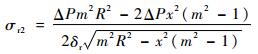(16)

由式(14)、式(16)可知，椭球上底经向应力σ_r1>0恒为拉应力，当R₂>2R₁时，σ_r2 < 0为压应力，当R₂ < 2R₁时，σ_r2>0为拉应力。
结合x²/a²+y_r²/b²=1，则式(14)与式(16)可表示为

(17)

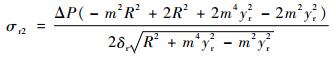(18)

1.3 贮箱圆柱筒应力 贮箱圆柱筒为大型薄壁壳体，在不考虑局部弯曲应力影响的条件下，建立贮箱圆柱筒数学模型，如图 3所示。图中：h为贮箱圆柱筒液面高度；δ_c为贮箱圆柱筒壁厚。

图 3 贮箱圆柱筒模型 Fig. 3 Cylinder model of tank

图选项

由内部增压引起的贮箱圆柱筒经向应力为

(19)

弯矩引起的贮箱圆柱筒经向应力为

(20)

式中：B为最大弯矩。
轴向压力引起的贮箱圆柱筒经向应力为

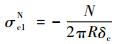(21)

式中：N为轴向压力。
可得贮箱圆柱筒经向应力为

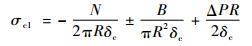(22)

式中：正号表示拉应力，负号表示压应力。
贮箱圆柱筒在内部增压ΔP及推进剂液体压力gnρh_c的作用下，其环向应力为

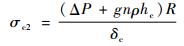(23)

式中：h_c=y_c为贮箱圆柱筒参考面液面高度。
2 区间凸模型可靠性指标确定 本文为有效解决推进剂贮箱在不确定性条件下的可靠性评估问题，结合应力干涉理论与正则化区间面积比方法，确定出贮箱应力强度区间凸模型可靠性指标。
如果参数P在某区间内变化，其上界、下界分别为P_max和P_min，则称P为区间变量，定义

(24)

式中：P^c为均值；P^r为离差。
则区间变量的上、下界可表示为

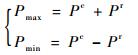(25)

区间变量P可表示为

(26)

式中：-1≤δ≤1为标准化区间变量。
本文将贮箱的临界应力设为区间变量J，等效应力设为区间变量S，则根据强度可靠性理论，定义贮箱应力强度可靠性临界状态函数为

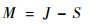(27)

对J与S进行正则化变换，据式(26)可得

(28)

式中：J^c和J^r分别为J的均值和离差；S^c和S^r分别为S的均值和离差；-1≤δ_J≤1与-1≤δ_S≤1分别为J与S的正则化区间变量。
根据结构可靠性理论，(J^c-J^r)-(S^c+S^r)表示贮箱临界应力与等效应力的干涉区域，如果存在应力干涉区，表示贮箱应力强度处于非完全可靠状态，如果不存在应力干涉区，表示贮箱应力强度处于完全可靠状态。
因此，当(J^c-J^r)>(S^c+S^r)时，贮箱区间凸模型可靠性指标定义为

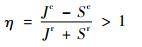(29)

据式(29)可知，此时η>1，即贮箱应力强度处于完全可靠状态。
当(J^c-J^r)≤(S^c+S^r)时，存在η≤1，即贮箱处于非完全可靠状态，为有效地表示贮箱处于非完全可靠状态下的可靠度，将η规范量化到[0, 1]范围内。将式(28)代入式(27)，可得贮箱正则化可靠性临界状态函数为

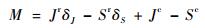(30)

在δ_S与δ_J组成的正则化坐标系中，式(30)与δ_S=0及δ_J=0的交点为(0, -(J^c-S^c)/J^r)，((J^c-S^c)/S^r, 0)。
贮箱临界状态函数与正则化区间的关系，如图 4所示。

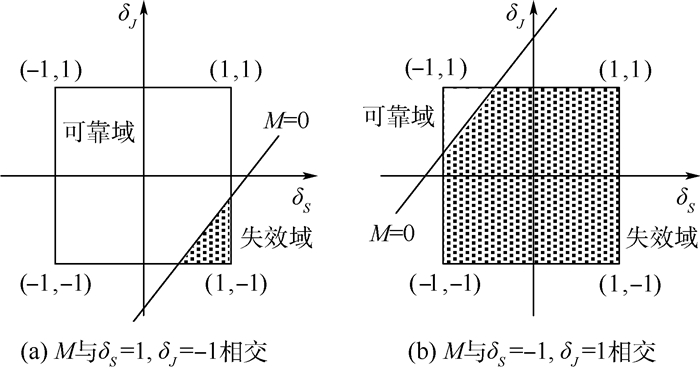图 4 临界状态函数与正则化区间 Fig. 4 Critical state function and regularized interval

图选项

据图 4(a)可知，在正则化坐标系中，临界状态函数M与δ_S=1、δ_J=-1的交点分别为(1, (S^c+S^r-J^c)/J^r)和((J^c-J^r-S^c)/S^r, -1)。
则可得贮箱正则化区间内的可靠域面积为

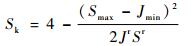(31)

式中：S_max为贮箱等效应力上限；J_min为贮箱临界应力下限。
据图 4(b)可知，在正则化坐标系中，临界状态函数M与δ_S=-1、δ_J=1的交点分别为(-1, (S^c-S^r-J^c)/J^r)和((J^c+J^r-S^c)/S^r, 1)。
则可得贮箱正则化区间内的可靠域面积为

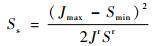(32)

式中：J_max为贮箱临界应力上限；S_min为贮箱等效应力下限。
本文将正则化区间可靠域面积S_s与正则化区间总面积S_t=4的比值，定义为贮箱在非完全可靠状态下的区间凸模型可靠性指标

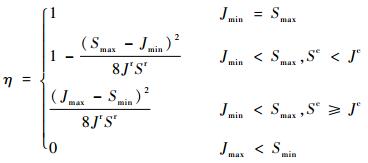(33)

因此，综合式(29)与式(33)可知，贮箱应力强度的任意可靠状态均可由η∈[0, +∞)来表示。当η>1时，表示贮箱应力强度处于完全可靠状态，η值表示贮箱的剩余应力强度；当η=0时，表示贮箱处于完全失效状态；当0 < η < 1时，表示贮箱应力强度处于非完全可靠状态，η值表示贮箱的应力强度可靠度；当η=1时，表示贮箱处于完全可靠与非完全可靠的临界状态。
3 实例验证 3.1 等效应力区间凸集确定 基于材料强度理论，根据贮箱椭球下底、上底与贮箱圆柱筒的应力分布情况，等效应力σ_e定义为

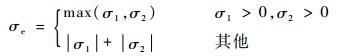(34)

式中：σ₁为经向应力；σ₂为环向应力。
以某型火箭推进剂贮箱参数(如表 1所示)为例，进行实例验证分析。
表 1 贮箱及推进剂参数 Table 1 Parameters of tank and propellant

参数	m	a/mm	h/mm	ρ/(kg·m-3)	ΔP/Pa
数值	1.6	1 669	8 080	1 458	101 325

表选项






贮箱通常由铝合金壁板焊接而成，其壁厚是影响贮箱应力强度可靠性的重要参数，某型火箭贮箱椭球下底、上底的壁厚参数，如表 2所示。
表 2 下底、上底壁厚参数 Table 2 Thickness parameters of bottom and roof

区间/mm	δb/mm	δr/mm
0≤yb(yr) < 695	2.3	2.0~5.5
695≤yb(yr)≤b	3.8	6.0~8.5

表选项






根据式(8)、式(9)与式(11)，取n=1，可得椭球下底经向应力与环向应力，如图 5所示。

图 5 下底经向应力与环向应力 Fig. 5 Meridional stress and hoop stress of bottom

图选项

据图 5可知，贮箱椭球下底经向应力与环向应力，均沿y_b的方向逐渐增大，但在不同壁厚壁板的焊接处存在明显的应力阶跃现象。椭球下底经向应力始终为拉应力, 即σ_b1>0。椭球下底环向应力于0.463 m处，由压应力转变为拉应力

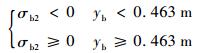(35)

假设椭球上底壁厚在对应区间内呈线性变化，对δ_r进行线性化转换，可得

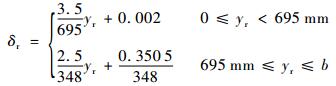(36)

根据式(17)、式(18)与式(36)，可得椭球上底经向应力与环向应力，如图 6所示。

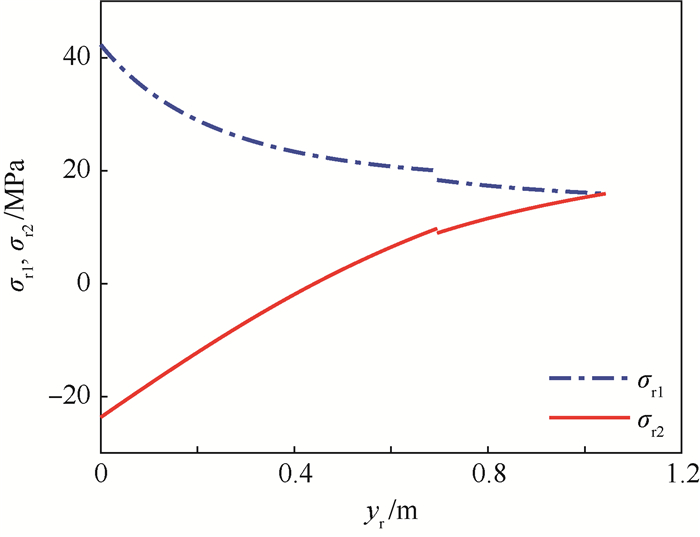图 6 上底经向应力与环向应力 Fig. 6 Meridional stress and hoop stress of roof

图选项

由于椭球上底为变壁厚设计，据图 6可知，椭球上底经向应力与环向应力的阶跃现象得到了改善。椭球上底经向应力沿y_r方向逐渐增大，始终为拉应力即σ_r1>0。椭球上底环向应力于0.442 m处，由压应力转变为拉应力，即

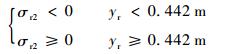(37)

贮箱圆柱筒由化铣铝合金壁板焊接而成，通常采用内加筋网格结构，可将贮箱内加筋网格结构转化为等效壁厚^[17]

(38)

式中：A为加筋截面积；d为加筋肋间距。某型火箭贮箱圆柱筒壁厚δ_c为3.5 mm，肋间距195 mm、肋高12 mm、肋宽10 mm，据式(38)可得圆柱筒等效壁厚δ_e为4.1 mm。
在内部增压、最大弯矩与轴向压力的共同作用下，贮箱圆柱筒的轴压失稳临界应力σ_i为

(39)

式中：E为弹性模量，取70 GPa。
在研究贮箱圆柱筒应力强度可靠性时，必须要保证贮箱圆柱筒的轴压稳定性。因此，将σ_c1取为确保贮箱圆柱筒处于轴压稳定状态的轴压失稳临界压应力-σ_i。
根据式(23)、式(38)与式(39)，取n=1，可得贮箱圆柱筒经向应力与环向应力，如图 7所示。

图 7 圆柱筒经向应力与环向应力 Fig. 7 Meridional stress and hoop stress of cylinder

图选项

据图 7可知，贮箱圆柱筒经向应力与y_c无关，始终为压应力；贮箱圆柱筒环向应力随y_c的增加呈逐渐递增的线性分布，始终为拉应力。
根据贮箱椭球下底、上底及贮箱圆柱筒的经向应力与环向应力分布，结合式(34)，将等效应力转换为区间凸集的形式，如表 3所示。
表 3 等效应力区间凸集 Table 3 Interval convex set of equivalent stress

MPa
结构	Smin	Smax
下底	66.27	137.13
上底	15.91	65.96
圆柱筒	213.25	261.20

表选项






3.2 区间凸模型可靠性分析 推进剂贮箱作为大型焊接结构，由于其焊接缺陷、应变裂纹及外界振动等不确定因素，导致其临界应力强度σ_s远小于材料极限应力强度σ_u，在实际应用过程中存在高度的不确定性，难以获得其真实的概率分布，通常根据试验获得的削弱系数来表示，即

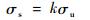(40)

式中：k为材料极限强度削弱系数；σ_u为材料极限应力，取415 MPa。
本文由区间凸集的形式来表示贮箱临界应力的不确定性，在k分别为0.7、0.8，0.6、0.7和0.5、0.6的3种情况下，确定相应的临界应力区间凸集，计算出贮箱应力强度可靠性指标，如表 4所示。
表 4 贮箱应力强度可靠性指标 Table 4 Stress strength reliability index of tank

结构	指标	k=0.7, 0.8	k=0.6, 0.7	k=0.5, 0.6
下底	η	3.73	2.99	2.25
	ηe	5.10	4.09	3.08
上底	η	5.91	5.00	4.09
	ηe	8.32	7.04	5.76
圆柱筒	η	1.66	0.96	0.32
	ηe	2.33	1.03	-0.28

表选项






η_e为在结构安全可靠性研究中，广泛应用的椭球凸模型非概率可靠性指标^[18]

(41)

将本文方法计算所得的可靠性指标η与椭球凸模型可靠性指标η_e进行对比分析可知：当贮箱处于完全可靠状态时，均存在η < η_e，表明在相同条件下，本文方法计算出的贮箱剩余强度小于椭球凸模型计算出的剩余强度，即可靠性指标η可以得到更为保守的可靠性评估结果。在实际应用中，推进剂贮箱对可靠性具有较高的要求，η更适合于对贮箱应力强度的可靠性进行评估。
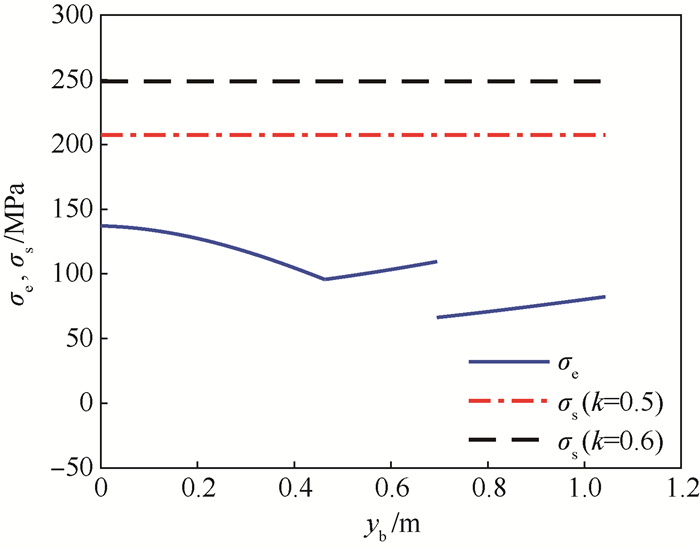
当k为0.5、0.6时，贮箱椭球下底、上底等效应力与临界应力区间凸集，如图 8、图 9所示。

图 8 下底等效应力与临界应力 Fig. 8 Equivalent stress and critical stress of bottom

图选项

图 9 上底等效应力与临界应力 Fig. 9 Equivalent stress and critical stress of roof

图选项

据图 8、图 9可知，当k为0.5、0.6时，贮箱椭球下底、上底等效应力与临界应力区间凸集始终存在J_min>S_max，贮箱处于完全可靠状态。据表 4可知，此时η值分别为2.25、4.09，即η>1，表示贮箱椭球下底、上底处于完全可靠状态。同理，当k分别为0.6、0.7和0.7、0.8时，贮箱椭球下底、上底的完全可靠状态与η的评估结果一致。
当k分别为0.5、0.6、0.7时，贮箱圆柱筒等效应力与临界应力区间凸集，如图 10所示。

图 10 圆柱筒等效应力与临界应力 Fig. 10 Equivalent stress and critical stress of cylinder

图选项

据图 10可知，当k为0.7、0.8时，贮箱圆柱筒等效应力与临界应力区间凸集有J_min>S_max，贮箱处于完全可靠状态，与η的评估结果一致。当k为0.6、0.7时，贮箱圆柱筒等效应力与临界应力区间凸集有J_min < S_max，即贮箱处于非完全可靠状态。据表 4可知，此时贮箱的η_e值为1.03，表示贮箱仍为完全可靠状态。而本文方法求得的η值为0.96，表示贮箱处于非完全可靠状态，可靠度为0.96，与实际相符。
当k为0.5、0.6时，贮箱圆柱筒等效应力与临界应力区间凸集有S^c < J^c，贮箱处于非完全可靠状态。据表 4可知，η_e值为-0.28，表明贮箱处于非完全可靠状态，但并不能评估贮箱的可靠度。而本文方法求得的η值为0.32，表明贮箱处于非完全可靠状态，且其可靠度为0.32。
综上所述，η不仅可以准确的表示贮箱应力强度的完全可靠状态，而且可以将贮箱应力强度的非完全可靠状态规范量化到0~1范围内，表示贮箱处于非完全可靠状态下的可靠度。
4 结论 1) 贮箱壁厚的变化会造成贮箱椭球下底、上底应力的阶跃现象，壁厚的线性化设计可削弱应力的阶跃现象，为贮箱的优化设计提供参考。
2) 贮箱应力强度区间凸模型可靠性指标η>1时，可准确评估贮箱的完全可靠状态，与贮箱应力强度的真实可靠状态相符。
3) 应用可靠性指标η可将贮箱应力强度的非完全可靠状态量化到[0, 1]区间，表示贮箱处于非完全可靠状态下的可靠度。

参考文献

[1]	王心清. 结构设计[M]. 2版. 北京: 中国宇航出版社, 2009: 19-35. WANG X Q. The structural design[M]. 2nd ed. Beijing: China Astronautic Publishing House, 2009: 19-35. (in Chinese)
[2]	张俊苗.航天器贮箱铝合金焊接接头强度特性研究[D].南京: 南京航空航天大学, 2013: 1-14 ZHANG J M.Investigation on strength properties of alumini-um alloy weld joint in spacecraft tank[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2013: 1-14(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1014059456.htm
[3]	NACHTIGALL I, GEBBEKEN N, URRUTIA-GALICIA J L. On the analysis of vertical circular cylindrical tanks under earthquake excitation at its base[J]. Engineering Structures, 2003, 25(2): 201-213. DOI:10.1016/S0141-0296(02)00135-9
[4]	JHA A K, NARAYANAN P R, SREEKUMAR K, et al. Cracking of Al-4.5Zn-1.5Mg aluminium alloy propellant tank-A metallurgical investigation[J]. Engineering Failure Analysis, 2010, 17: 562-570. DOI:10.1016/j.engfailanal.2009.10.009
[5]	JHA A K, MURTY S V S N, SREEKUMAR K, et al. High strain rate deformation and cracking of AA 2219 aluminium alloy we-lded propellant tank[J]. Engineering Failure Analysis, 2009, 16(7): 2209-2216. DOI:10.1016/j.engfailanal.2009.03.001
[6]	BEN-HAIM Y. Convex models of uncertainty in applied mecha-nics[M]. New York: Elsevier Science Publishers, 1990: 151-157.
[7]	BEN-HAIM Y. A non-probabilistic concept of reliability[J]. Structural Safety, 1994, 14(4): 227-245. DOI:10.1016/0167-4730(94)90013-2
[8]	ELISHAKOFF I, BEN-HAIM Y. Dynamics of a thin cylindrical shell under impact with limited deterministic information on its initial imperfections[J]. Structural Safety, 1990, 8(1): 103-112.
[9]	邱志平, 胡永明. 椭球凸模型非概率可靠性度量和区间安全系数的关系[J]. 计算力学学报, 2016, 33(4): 522-527. QIU Z P, HU Y M. The relations of non-probabilistic reliabilitymeasures based on ellipsoidal convex model and interval safety factors[J]. Chinese Journal of Computational Mechanics, 2016, 33(4): 522-527. (in Chinese)
[10]	王晓军. 不确定初始几何缺陷杆动态屈曲失效分析[J]. 北京航空航天大学学报, 2011, 37(12): 1484-1489. WANG X J. Dynamic buckling failure analysis of rod with uncertain initial geometrical imperfection[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(12): 1484-1489. (in Chinese)
[11]	WANG R X, WANG X J, WANG L, et al. Efficient computational method for the non-probabilistic reliability of linear structural systems[J]. Acta Mechanica Solida Sinica, 2016, 29(3): 284-301. DOI:10.1016/S0894-9166(16)30162-8
[12]	JIANG C, BI R G, LU G Y, et al. Structural reliability analysis using non-probabilistic convex model[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 254: 83-98. DOI:10.1016/j.cma.2012.10.020
[13]	GUO S X, LU Z Z. A non-probabilistic robust reliability method for analysis and design optimization of structures with uncertain-but-bounded parameters[J]. Applied Mathematical Modelling, 2014, 26: 3-15.
[14]	COURTOIS C, DENUIT M. Bounds on convex reliability functions with known first moments[J]. Stochastics and Statistics, 2007, 177(1): 365-377.
[15]	KARUNA K, MANOHAR C S. Inverse problems in structural safety analysis with combined probabilistic and non-probabilistic uncertainty models[J]. Engineering Structures, 2017, 150: 166-175. DOI:10.1016/j.engstruct.2017.07.044
[16]	赵亮.大直径薄壁箱体结构力学分析与精细优化设计[D].大连: 大连理工大学, 2015: 32-36. ZHAO L.The mechanical analysis and refined optimization of large-diameter and thin-walled tank structures[D].Dalian: Dalian University of Technology, 2015: 32-36(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10141-1015357272.htm
[17]	刘雨均. 运载火箭总体与结构[M]. 北京: 国防工业出版社, 2003: 206-217. LIU Y J. Launch vehicle overall and structure[M]. Beijing: National Defence of Industry Press, 2003: 206-217. (in Chinese)
[18]	张娜.非概率可靠度理论相关问题研究[D].柳州: 广西科技大学, 2015: 17-22. ZHANG N.The research of non-probability reliability[D].Liuzhou: Guangxi University of Science and Technology, 2015: 17-22(in Chinese).