对于具有严格周期性要求的TT流量[7],可调度性的分析与测试方法可以借鉴文献[8]引入的干涉时间的概念,以及文献[9-10]关于多处理器下严格周期任务可调度性判定的相关方法,进而将严格周期可调度性的测试方法引入到TT流量调度表增量化生成中;更进一步,笔者发现SMT增量化求解过程不仅受限于是否可调度,而且其计算效率和回溯次数与流量集合可调度的难易程度有关。
本文的贡献在于,提出了一种基于可调度性排序的增量化时间触发调度表生成方法。不仅可以通过TT可调度性测试先排除完全不可调度的情况,而且在SMT增量化求解过程中,充分认识到严格周期利用率因子(SPU)[11]对于TT流量可调度性的综合量化能力,依据SPU值对流量按调度难度降序排列,在给定的求解步长下将流量分批,组成可调度性能依次递减的流量子集,先难后易增量化求解;并且,通过计算已调度集合对未调度集合的干涉时间得到未调度流量发送时刻的可行范围,起到缩减约束数量的作用,使计算效率不仅优于原始的SMT调度求解方法[5],而且在网络规模较大的情况下,回溯次数显著低于随机和周期升序排序的增量化调度方法。另外,在“干涉时间”的论证过程中,给出一种基于时间轴延拓的干涉时间计算方法;与原来的将每个消息传输时刻对周期取模[8]的方法相比,更加易于理解。
本文首先介绍了TT流量的调度约束条件,并归纳了单网段下新增TT流量的可调度性判定规则;其后,详细阐明基于可调度性排序的TT流量增量化调度表生成方法;最后,通过案例研究和对照组实验展示了本文所提出的调度方法的高效性。
1 TT流量的调度约束条件 TTE的物理拓扑可表示为一个无向图G=(V, E),其中节点集V代表端系统和交换机,边集E代表连接节点的物理通信链路。物理链路仅存在于交换机节点间或一个交换机和一个端系统节点间;每条物理链路(电/光缆)都是全双工通信,以(v1, v2)表示,其中v1, v2∈V;而物理链路中包含的双向数据流链路(Dataflow Link, DL),以[v1, v2]和[v2, v1]来表示。
在TTE中,每条TT流量都以帧(消息)的形式周期性地传输。设FTT={f1, f2, …, fn}为一个包含n条TT流量的集合,每条流量fi都有且仅有一个源节点(端系统),并通过树状路径Pi连接到一个或多个目的节点(端系统)。这种树状路径Pi可以表示为一组数据流链路的集合,即Pi={Li, 1, Li, 2, …, Li, m}。
用一个四元组来表示一条TT流量fi:
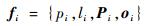 | (1) |
式中:pi为流量的周期;li为帧长(消息的传输时间);oi为一个集合,表示流量fi在其经过的所有数据流链路上的起始发送时刻(第1个帧的发送时刻),即oi={oi(Li, 1), oi(Li, 2), …, oi(Li, m)}。因为TT流量基于严格周期发送,即流量fi在链路Li, k上的任意第r个帧的发送时刻为oi, r(Li, k)=oi, 1(Li, k)+(r-1)pi,所以只需考虑第1个帧的发送时刻,此后令oi(Li, k)=oi, 1(Li, k)。在实际应用中,选取合适的时间单位将pi和li规范为正整数,且令oi(Li, k)的取值为非负整数。
在TTE中,TT流量的起始发送时刻oi需要满足一系列的约束条件[5, 7, 12]。
1) 流量周期约束。任意一条TT流量的第1个帧在其经过的所有数据流链路上的派发时刻应限制在第1个周期内。
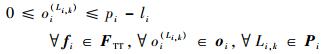 | (2) |
2) 无冲突约束。任意一条数据流链路上,不同流量的帧发送时间区间互不重叠。即对于?fi∈FTT和fj∈FTT,且i≠j,如果它们经过某条相同的数据流链路Li, k=Lj, h,则对于取值范围为

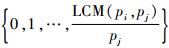
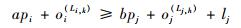 | (3) |
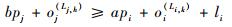 | (4) |
3) 路径依赖约束。TT流量的单跳延迟有范围限制。min(dhop)为单跳延迟下限,由物理链路固定传输延迟决定;max(dhop)为单跳延迟上界,由交换机的内存大小决定。
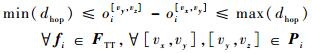 | (5) |
4) 中继同步约束。对于多播流量fi,由相同节点分叉出的路径上消息的发送时刻相同。
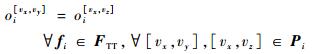 | (6) |
5) 端到端传输约束。限定流量从源节点到目的节点的端到端最大允许传输延迟为max(dlatency)。设流量fi有Q个目的节点(Q为正整数,Q≥1),不失一般性,令源节点对应的起始链路序号为1,对应目的节点的末端链路序号为mq(q=1, 2, …, Q)。
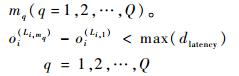 | (7) |
6) 应用层约束。在应用层,由于不同的TT流量有不同的任务要求,所以可限定从同一端系统节点出发的所有TT的起始发送时刻的最小间隔δ[13],设所有TT源端起始链路序号均为1。
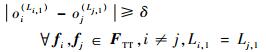 | (8) |
7) 协议控制帧(PCF)约束。在TTE中,各个通信节点本地时钟的同步,通过时钟同步消息的交换来实现,这种时钟同步消息即PCF帧。因此,PCF帧的传输相比普通TT流量有更高的优先级,即TT流量的调度不能与PCF帧占用的时间资源冲突。
2 新增TT流量的单网段可调度性 TT流量遵循严格周期调度的形式。在某一条数据流链路(单网段)上的TT流量调度问题等价于单处理器下的严格周期任务调度问题。第1节中约束1)、约束2)决定了TTE网络整体配置的可行性,是新增TT流量在每个网段必须满足的条件。由于这些必要性条件易于检查,在SMT求解之前可以快速排除不满足无冲突约束的新增流量。
将文献[10]中的严格周期任务的判定条件推广到TT流量,作为单网段可调度性的判定依据。
定理1??对?fi, fj∈FTT,i≠j,若有Li, k∈Pi,Lj, h∈Pj,Li, k, Lj, h∈Pi∩Pj且设Li, k和Lj, h是同一条数据链路,则2条流量在这条数据流链路上无冲突传输的充要条件如式(9)所示:
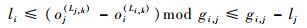 | (9) |
式中:gi, j为pi和pi的最大公约数。
设网络中已存在具有可行调度的流量集合FTT={f1, f2, …, fn},需要考查新增单条流量fr在其某个数据流链路Lr, s上的可调度性问题。
借鉴文献[8]的“干涉时间”概念,即待考查的流量经过的某一条数据流链路Lr, s,存在已获得调度的其他流量,则在新增流量fr一个周期内的时间单元集合Tr={0, 1, …, pr-2, pr-1}中会有部分单元已占用。对于给定的某条已获得调度的流量,可以将其每个消息的释放时刻对pr取模[8]评价其对于新增流量的干涉情况;但本文给出并证明的方法(参见定理2)是从已存在流量的初始时刻合理延拓时间轴,在一些离散时刻进行检测,同样可以得到干涉情况,且具有更直观的效果。
定理2(基于时间轴延拓的干涉时间计算方法)网络中2条流量fi、fr,若存在Li, k∈Pi、Lr, s∈Pr,且恰好Li, k和Lr, s是同一条数据链路(记为Li, k=Lr, s),则流量fi在该数据链路上对fr干涉的时间单元集合I(i, k, r, s)可由式(10)计算得到:
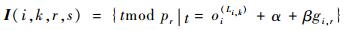 | (10) |
式中:t为离散时间点;gi, r为pi和pr的最大公约数;α和β为非负整数,取值为α=0, 1, …, (li-1)和β=0, 1, …, (pr/gi, r-1)。
证明??为保证2条流量fi和fr无冲突传输,由式(9)可得,orLr, s不能选取(会发生冲突)的全部时间单元在
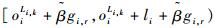
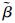
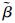
根据定理2,可以求出流量集合FTT在链路Lr, s上对fr的全部干涉时间单元集合:Iall(r, s)=
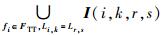
然后,再计算排除干涉时间单元后Tr中剩余的连续空闲时间长度的最大值,若该值大于等于lr,则fr在Lr, s上可以严格周期调度[8]。引用文献[9]中定义的函数LLC(
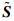
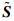
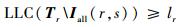 | (11) |
3 增量化TT调度表生成方法 3.1 方法步骤 基于可调度性排序的增量化TT调度表生成方法的总体步骤如下:
步骤1??先对集合FTT进行可调度性测试,具体包括端系统测试和交换机测试:如果测试未通过,则返回“不可调度”;若测试通过,继续步骤2。
步骤2??通过计算TT流量的SPU,将集合FTT中的流量按照可调度性由难到易的顺序进行排序,排序结果对应为TT流量序列RTT=[fR1, fR2, …, fRn]。
步骤3??每次增加的流量条数被称为SMT增量化求解的“步长”,记为变量Δ,并设当前待求解流量的序号范围为B~E(即E=B+Δ-1);初始化参数:B=1,E=Δ;并在SMT求解器中创建一个逻辑上下文语境,用于存储添加的约束,记作“CTX”。
步骤4??清空CTX,并根据第1节所述,生成待调度流量集合FTT_curr={fRi|i=B, B+1, …, E}的调度约束,并将生成约束增加到CTX中;其中“无冲突约束”和“应用层约束”均包含两部分,即“已调度流量集合FTT_succ={fRi|i=1, 2, …, B-1}和待调度集合FTT_curr之间”、“待调度集合FTT_curr内部”,其他约束只需考虑待调度集合FTT_curr内部。
步骤5??调用SMT求解器检查CTX的可满足性,若“满足”,则可从SMT求解器中获取满足CTX中所有约束的一个模型(model),它是待调度集合FTT_curr中流量发送时刻的一组可行解,记录之,执行步骤6;若“不满足”,执行步骤7。
步骤6??调整参数:B=E+1,E=min(B+Δ-1, n);若B>E,结束调度方法,返回“调度成功”,否则继续步骤4。
步骤7??若B=1,结束调度方法,返回“调度失败”;否则,执行回溯操作:B=max(B-Δ, 1),继续步骤4。
3.2 TT可调度性测试 类比于文献[10]中严格周期任务调度意义下的厚度概念,定义一组TT流量FTT_group={f1, f2, …, fm}的厚度CTT_group为按严格周期形式传输TT集合FTT_group中所有流量所需的数据流链路的数目。
将多处理器下严格周期任务的可调度性分析方法[9]推广到流量厚度CTT_group的计算中。将集合FTT_group中的TT流量逐条放到数据流链路上;在已有的TT流量的基础上,由于只是逐条增加,并不涉及新增流量之间的可调度性计算;该方法的关键是判断单个数据流链路在已调度的TT流量基础上,是否能够无冲突传输新增的某条TT流量,这一判断可以利用定理2计算干涉时间,通过式(11)来完成。
基于TT流量的厚度计算,可以对TTE网络中待调度的TT流量集合进行如下的可调度性测试。
1) 端系统测试:对TTE网络中的每个端系统,分别统计其发出、接收的TT流量集合FTT_out、FTT_in;测试通过准则为CTT_out≤1且CTT_in≤1。
2) 交换机测试:对于含有多级交换机SW的网络,端系统ES接入的交换机通过各个端口与下一级交换机全双工互连。检查对象为端系统接入的交换机SW*(N>M),如图 1所示。设交换机SW*所连接的N个端系统集合为V1,TTE网络中的其余端系统集合为V2,统计源端系统属于V1目的端系统属于V2的TT流量集合为FTT_out,而源端系统属于V2目的端系统属于V1的TT流量集合为FTT_in;测试通过准则为CTT_in≤M且CTT_out≤M。
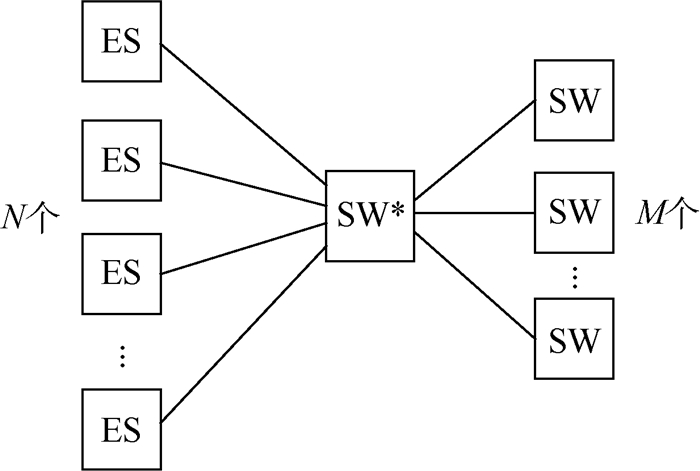 |
| 图 1 端系统接入的交换机示意图 Fig. 1 Schematic diagram of switch accessed by end systems |
| 图选项 |
3.3 考虑可调度性的TT流量排序 TTE要求所有TT流量均可调度,因此在求解次序的安排上,将TT流量按照可调度难度降序排列;在排序过程中,流量的可调度性难度是用SPU[11]来衡量的。具体方法如下:
输入:待排序的TT流量集合FTT={f1, f2, …, fn}。
输出:以可调度性增序排列的TT流量序列RTT=[fR1, fR2, …, fRn],重新排序的索引集合{Ri}, i=1, 2, …, n。
步骤1??将FTT赋予某临时变量集合S存储,令RTT为空集?。
步骤2??如果S为空集,则结束运算,输出RTT;否则执行步骤3。
步骤3??分别计算集合S中流量fi的SPU值,作为严格周期利用率因子uS(i),如式(12)所示:
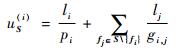 | (12) |
式中:uS(i)由两部分计算累加而成;
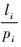
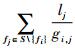
步骤4??uS(i)值越小,则在S\{fi}中的流量已经被调度的条件下,新增流量fi无冲突调度的可能性越大,调度难度越小;找到集合S中使uS(i)最小的TT流量,并将它的索引记为k。
步骤5??将流量fk从集合S中移除,并将fk添加到RTT序列的最前端,形成按照SPU值降序的序列,随后返回执行步骤2。
3.4 无冲突约束规模的缩减 在增量化TT调度表求解中,一次只生成流量的序号范围为B~E的TT流量子集(待调度集合FTT_curr)的调度约束(3.1节步骤4)。在TT流量的几类调度约束中,无冲突约束数量最多,且最为重要,用于保证网络中所有TT流量传输的时间区间互不重叠。
在生成待调度集合FTT_curr的无冲突约束时,不仅要考虑FTT_curr内部的TT流量之间互不冲突,还要确保这部分TT流量与网络中已调度流量集合FTT_succ间的无冲突传输;其中后者的约束数目会随着B值的增长而迅速增加。
考虑到网络中已调度流量FTT_succ的调度表已知,所以对于FTT_curr与FTT_succ间的无冲突约束生成,可以不采用传统的规范形式(见式(3)和式(4)),而采用集合间无冲突约束的生成方法。通过计算网络已调度流量FTT_succ在Lr, s上对流量fr(fr∈FTT_curr)的干涉时间,求出fr在Lr, s上的空闲时隙集合Tfree(r, s);再从集合Tfree(r, s)中顺次寻找连续整数长度大于等于消息长度的区间,进而得到or(Lr, s)的可行取值范围。集合间无冲突约束的生成方法如下:
输入:TT流量的已调度集合FTT_succ和待调度集合FTT_curr,SMT求解器中用于存储约束的逻辑上下文语境CTX。
输出:FTT_succ和FTT_curr集合之间的经过优化的无冲突约束,并添加到CTX中。
步骤1??令流量序号r=1,路径序号s=1。
步骤2??在待调度集合FTT_curr中选取第r条流量fr。
步骤3??选取流量fr所对应的路径集合Pr中第s段数据链路Dr, s。
步骤4??计算已调度流量在数据链路Dr, s上对fr的干涉时间单元,并赋给集合ITT_succ(r, s)。
 | (13) |
步骤5??在流量fr的1个周期内的时间单元集合Tr中排除受干涉的时间单元,并赋给集合Tfree(r, s)。
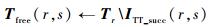 | (14) |
步骤6??在Tfree(r, s)中查找到第1个连续整数长度不小于消息长度lr的区间,设区间的左右端点为t1和t2,t1≤t2,记为闭区间[t1, t2];如果找不到这样的区间,则令t1=0和t2=0。
步骤7??如果[t1, t2]为[0, 0],则跳转到步骤10;否则形成约束如式(15)所示,并将该约束以逻辑“或”的关系添加到CTX。
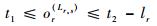 | (15) |
步骤8??在Tfree(r, s)中顺次查找到下一个连续整数长度不小于消息长度lr的区间,仍用t1和t2存储区间左右端点的值;如果找不到这样的区间,则令t1=0和t2=0。
步骤9??跳转到步骤7。
步骤10??如果Pr中还有未被选取的数据链路,则令s=s+1,跳转到步骤3。
步骤11??如果fr中还有未被选取的TT流量,则令r=r+1,s=1,跳转到步骤2;否则,结束运算,输出添加了新约束后的CTX。
如果采用令式(3)和式(4)同时成立的传统无冲突约束规范,为了保证与FTT_succ不冲突,or(Lr, s)的约束个数N1(r, s)如式(16)所示:
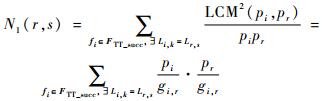 | (16) |
而采用集合间无冲突约束的生成方法,生成已调度流量FTT_succ与待调度流量FTT_curr间的无冲突约束,约束规模取决于可行区间[t1, t2]的个数。因此对于?fr∈FTT_curr, ?Lr, s∈Pr,与or(Lr, s)有关的约束个数范围为式(17),其中不等式右边为fr在Lr, s上空闲时隙集合Tfree(r, s)中连续整数区间个数的上限值。考虑到并非所有空闲区间的长度都能达到lr,并且FTT_succ中不同流量在Lr, s上对fr的干涉时间区间可能会有重叠,因此实际可行区间[t1, t2]的个数(即N2(r, s))通常会远小于这个上限值。
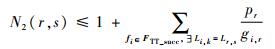 | (17) |
因为
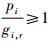
4 案例分析 4.1 测试案例的生成 为了对基于可调度性排序的增量化TT调度表生成方法的性能进行评价,本文生成了一系列不同规模的测试案例。案例的网络拓扑选取雪花型拓扑[7]。具体到本案例,如图 2所示,拓扑包含30个端系统,11个交换机,40条通信链路(80条数据流链路);为了叙述方便,定义与同一交换机(非中心交换机)相连的所有端系统为一个“瓣”,图 2中所示拓扑共有10个“瓣”。网络中的每个端系统都发送相同数目的TT流量,并根据雪花型网络拓扑的结构特点,将TT流量区分为下述4种类型:
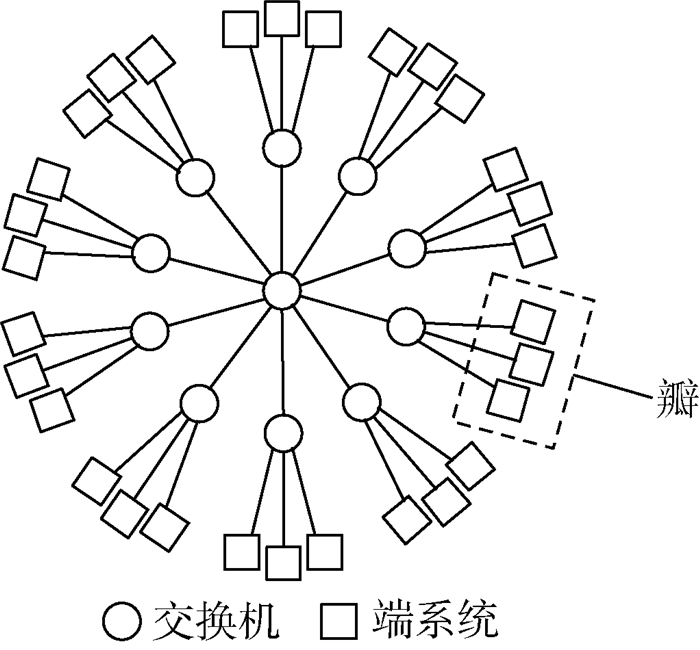 |
| 图 2 带有30个端系统的雪花型拓扑 Fig. 2 A snowflake topology with 30 end systems |
| 图选项 |
1) 局域内多播。源端系统将TT流量发送给仅经过单跳的所有端系统(即源端系统所属“瓣”内的其余端系统)。
2) 局域外多播。源端系统将TT流量发送给全网中2~3个“瓣”(不包括源端系统所在“瓣”)内的所有端系统。
3) 局域内单播。目的端系统为源端系统所属“瓣”内的某个端系统(不包括源端系统)。
4) 局域外单播。目的端系统为源端系统所属“瓣”外的某个端系统。
每个端系统可以发送任一种类型的TT流量,规定测试案例中各类型TT流量的数目与每个端系统发送TT数的关系如表 1所示。表中四元组(n1, n2, n3, n4)分别为局域内多播、局域外多播、局域内单播、局域外单播的TT流量数目。
表 1 4种TT流量类型的数量分布 Table 1 Quantity distribution of four kinds of TT traffic
| 每个端系统发送TT数 | 各类型TT流量数量 |
| 2 | (0,0,1,1) |
| 4 | (0,0,2,2) |
| 6 | (0,0,3,3) |
| 8 | (1,1,3,3) |
| 10 | (1,1,4,4) |
| 12 | (1,1,5,5) |
| 14 | (2,2,5, 5) |
| 16 | (2,2,6,6) |
| 18 | (2,2,7,7) |
表选项
TT消息的帧长在64~1 518 Byte中随机选取,周期取值为2x3yw ms,其中非负整数x, y∈{0, 1, 2}并等概率随机选取,基数w为正整数,全网带宽为100 Mbit/s。对于TT流量的调度约束参数设置,将min(dhop)设为130 μs,max(dhop)设为390 μs,端到端延迟上界max(dlatency)设为1 ms,应用层约束最小间隔δ设为50 μs。对于TTE网络中的同步开销,PCF帧长64 Byte,集成周期取值10 ms。
增量化调度表求解的步长Δ取值为6[14]。整个实验运行在Intel i5 3.20 GHz CPU的主机(4 GB内存)。
4.2 案例结果 原始的SMT调度表生成方法[5]没有考虑无冲突约束的缩减。图 3对比了无冲突约束规模缩减前后,不同测试案例规模(每个端系统发送TT数)下的增量化TT调度表生成所需时间;其中,TT流量的周期基数w∈{1, 5}。可以看出,经过无冲突约束规模缩减后,调度表求解时间得到大幅降低。这是因为,FTT_curr与FTT_succ集合间无冲突约束的生成方法使用干涉时间作为已调度流量集合整体对待调度流量的联合约束,代替了传统的两两TT流量的无冲突约束生成方法(式(3)和式(4)同时成立),从而大规模缩减约束数量,提高了调度表求解效率。
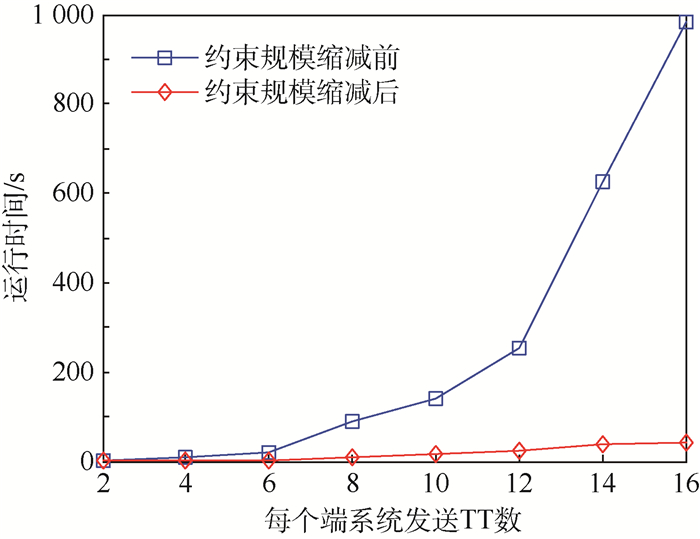 |
| 图 3 无冲突约束规模缩减前后运行时间对比 Fig. 3 Comparison of running time before and after contention-free constraints reduction |
| 图选项 |
为了评价不同TT流量排序方法下增量化TT调度表求解的性能,测试选取4种排序方法,分别是:随机排序(即不考虑可调度性)、周期升序(相当于可调度难度降序),基于SPU值计算的流量可调度难度降序排序(即3.3节步骤1~步骤7的方法,简称“SPU降序”),以及基于SPU值计算的流量可调度难度升序排序(简称“SPU升序”)。其中,“SPU升序”的排序方法是将3.3节步骤4中每次寻找SPU值最小的流量改为寻找SPU值最大的流量。
TT流量的周期基数w∈{1, 5, 7},使实验结果进一步展示非调和周期参数下[15]的调度性能。图 4给出了3种流量排序方法下,增量化TT调度表求解的回溯次数(3.1节步骤7的执行次数)对比;表 2为增量化调度表生成的运行时间对比。对于长期不停机的情况,增量化调度表求解设有时间上限,若超过该时间值仍没结束,则返回“无法判定”,本文设定时间上限为20 000 s。
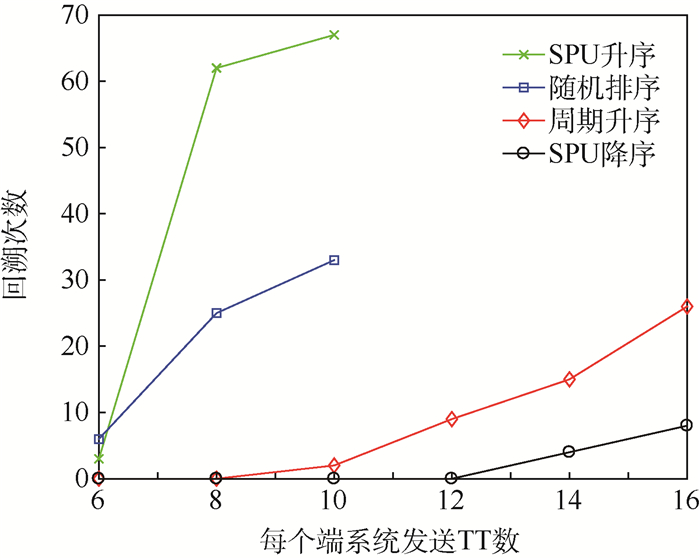 |
| 图 4 不同流量排序方法下的增量化求解回溯次数 Fig. 4 Backtracking times of incremental scheduling method under different traffic ranking methods |
| 图选项 |
表 2 不同流量排序方法下的运行时间 Table 2 Running time under different traffic ranking methods
| s | ||||||
| 排序方法 | 每个端系统发送TT数 | |||||
| 6 | 8 | 10 | 12 | 14 | 16 | |
| SPU升序 | 3 | 17 259 | 7 530 | — | — | — |
| 随机排序 | 27 | 1 951 | 914 | — | — | — |
| 周期升序 | 9 | 22 | 38 | 256 | 2 716 | 3 609 |
| SPU降序 | 10 | 21 | 41 | 44 | 78 | 662 |
表选项
综合图 4、表 2可以看出,随机排序由于没有考虑流量的可调度性因素,增量化求解过程的回溯次数明显高于按可调度难度降序排序的2种方法(周期升序和SPU降序),进而导致调度表生成所需的运行时间也大幅增加;而且,随着案例规模的增大,会出现“无法判定”的情况。对于周期升序和SPU降序,当案例规模不大时,增量化求解性能接近;而当网络中的TT流量规模较大时,本文提出的排序方法在增量化求解的回溯次数、运行时间方面,都明显低于周期升序;原因在于:TT流量的可调度性不仅取决于流量的周期大小,正如第2节所述,还与TT的帧长、不同TT间周期的最大公约数等因素有关;而本文的方法通过SPU值的计算,综合考虑进了这些影响可调度性的因素,排序结果更能反应流量的可调度难度的高低。
“SPU升序”是为了印证“SPU降序”的合理性而设置的对照组。从结果可以看出,它的增量化求解回溯次数和运行时间都明显高于可调度难度降序,甚至高于随机排序;这是因为它使流量按照可调度难度升序排列并依次接受调度,增量化求解的回溯主要发生在流量排序序列的后部,一旦开始回溯,可能会需要回溯多次直至在3.1节步骤5中得到“满足”的判断,才能继续执行3.1节步骤6新增流量子集进行调度。
5 结论 1) 本文提出了一种可用于TTE网络的基于可调度性排序的增量化时间触发调度表生成方法。
2) 在增量化调度表生成中,通过干涉时间的计算对无冲突约束规模进行缩减,可以大幅降低运行时间。
3) 案例研究表明,在网络中TT流量规模较大时,本文方法可以在一定程度上避免随机选取流量进行增量化调度时长期不停机导致的“无法判定”的情况,并且在增量化求解的回溯次数和运行时间方面均低于其他排序方法。
参考文献
| [1] | STEINER W, BAUER G, HALL B, et al.TTEthernet dataflow concept[C]//Proceedings of 8th IEEE International Symposium on Network Computing and Applications.Piscataway, NJ: IEEE Press, 2009: 319-322. |
| [2] | SAE AS-2 Committee.Time-triggered Ethernet: SAE AS6802[S].Warrendale, PA: SAE International, 2011. |
| [3] | 张英静, 熊华钢, 刘志丹, 等. 可用于航空电子系统的时间触发以太网[J]. 电光与控制, 2015, 22(5): 49-53. ZHANG Y J, XIONG H G, LIU Z D, et al. Application of TTE communication technology in avionics system[J]. Electronics Optics & Control, 2015, 22(5): 49-53. DOI:10.3969/j.issn.1671-637X.2015.05.012 (in Chinese) |
| [4] | STEINBACH T, LIM H T, KORF F, et al.Tomorrow's in-car interconnect? A competitive evaluation of IEEE 802.1 AVB and Time-Triggered Ethernet (AS6802)[C]//Proceedings of IEEE Conference on Vehicular Technology.Piscataway, NJ: IEEE Press, 2012: 1-5. |
| [5] | STEINER W.http://html.rhhz.net/BJHKHTDXXBZRB/An%20evaluation%20of%20SMT-based%20schedule%20synthesis%20for%20time-triggered%20multi-hop%20networks[C]//Proceedings of 31st IEEE Real-Time Systems Symposium (RTSS).Piscataway, NJ: IEEE Press, 2010: 375-384. http://html.rhhz.net/BJHKHTDXXBZRB/An%20evaluation%20of%20SMT-based%20schedule%20synthesis%20for%20time-triggered%20multi-hop%20networks |
| [6] | DE MOURA L, BJORNER N. Satisfiability modulo theories:Introduction and applications[J]. Communications of the ACM, 2011, 54(9): 69-77. DOI:10.1145/1995376 |
| [7] | POZO F, RODRIGUEZNAVAS G, STEINER W, et al.Period-aware segmented synthesis of schedules for multi-hop time-triggered networks[C]//Proceedings of IEEE, International Conference on Embedded and Real-Time Computing Systems and Applications.Piscataway, NJ: IEEE Press, 2016: 170-175. http://ieeexplore.ieee.org/document/7579952/ |
| [8] | 陈进朝, 杜承烈. 单处理器平台下的严格周期任务可调度性判定[J]. 计算机工程, 2016, 42(5): 288-291. CHEN J C, DU C L. Schedulability test for strictly periodic tasks on uniprocessor platform[J]. Computer Engineering, 2016, 42(5): 288-291. DOI:10.3969/j.issn.1000-3428.2016.05.050 (in Chinese) |
| [9] | CHEN J, DU C, XIE F, et al. Schedulability analysis of non-preemptive strictly periodic tasks in multi-core real-time systems[J]. Real-Time Systems, 2016, 52(3): 239-271. DOI:10.1007/s11241-015-9226-z |
| [10] | KORST J, AARTS E H L, LENSTRA J K, et al.Periodic multiprocessor scheduling[C]//Parallel Architectures and Languages Europe(PARLE).Berlin: Springer-Verlag, 1991, LNCS505: 166-178. |
| [11] | KERMIA O. Timing analysis of TTEthernet traffic[J]. Journal of Circuits Systems & Computers, 2015, 24(9): 1550140. |
| [12] | POZO F, STEINER W, RODRIGUEZ-NAVAS G, et al.A decomposition approach for SMT-based schedule synthesis for time-triggered networks[C]//Emerging Technologies & Factory Automation.Piscataway, NJ: IEEE Press, 2015: 1-8. https://www.researchgate.net/publication/308853509_A_decomposition_approach_for_SMT-based_schedule_synthesis_for_time-triggered_networks |
| [13] | 张英静, 何锋, 卢广山, 等. 基于TTE的改进加权轮询调度算法[J]. 北京航空航天大学学报, 2017, 43(8): 1577-1584. ZHANG Y J, HE F, LU G S, et al. A modified weighted round robin scheduling algorithm in TTE[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(8): 1577-1584. (in Chinese) |
| [14] | POZO F, RODRIGUEZ-NAVAS G, HANSSON H, et al.SMT-based synthesis of TTEthernet schedules: A performance study[C]//IEEE International Symposium on Industrial Embedded Systems.Piscataway, NJ: IEEE Press, 2015: 1-4. https://www.researchgate.net/publication/314921079_SMT-based_synthesis_of_TTEthernet_schedules_A_performance_study |
| [15] | SHEIKH A A. Strictly periodic scheduling in IMA-based architectures[J]. Real-Time Systems, 2012, 48(4): 359-386. DOI:10.1007/s11241-012-9148-y |
