环面蜗杆传动具有同时接触齿数多、蜗杆啮入端为双线接触、齿面诱导法曲率小并且滑动角接近90°等特点，这些特点使得环面蜗杆与蜗轮啮合时具有齿面接触应力小以及齿面间弹性流体动压润滑条件好等特性^[1]。因此, 环面蜗杆传动的承载能力强，传动效率高，广泛应用于矿冶、起重运输和船舶等的传动装置^[2-3]。组成环面蜗杆副的蜗轮主要由环面蜗轮滚刀滚切而成，由于环面蜗轮滚刀各个刀齿的形状不同、滚刀基本蜗杆齿面螺旋线上各处的螺旋升角也不相同，导致环面蜗轮滚刀的制造比较复杂，特别是环面蜗轮滚刀前刀面的成形及加工方法，将影响刀齿的切削性能和滚切蜗轮的效率^[4-6]。
对于头数较少的环面蜗轮滚刀，为便于加工制造，通常采用直容屑槽^[6]。董李扬^[7]和柳冠伊^[8]建立了直容屑槽环面蜗轮滚刀前刀面的数学模型并对直容屑槽滚刀进行了加工制造。采用直容屑槽时，滚刀刀齿一侧是正前角，另一侧是负前角^[9-11]；滚刀头数较多时，绝对值较大的负前角一侧引起主切削力增大，导致切削条件恶劣甚至无法加工，因此需要采用螺旋容屑槽前刀面，以降低刀齿负前角的绝对值，并均衡刀齿左右两侧的切削条件^[12-14]。
杨杰等^[9-11]研究了由圆柱产形面加工螺旋容屑槽环面蜗轮滚刀前刀面的方法，但是，此方法采用的圆柱形刀具加工效率较低。Chang^[15]采用盘形铣刀加工圆柱滚刀前刀面的方法，提高了加工效率，适用于螺旋容屑槽的粗加工，但是，对于前刀面的精加工，通常需要采用盘形砂轮磨削的方法。采用平面砂轮加工直容屑槽滚刀的前刀面是可行的，但是磨削螺旋容屑槽前刀面时会出现非常明显的中凸现象，同时易产生砂轮平面与刀齿干涉的问题^[16]；为避免上述问题，刘杰华^[17]采用修形轴截面的平面砂轮磨削齿轮滚刀的螺旋容屑槽前刀面。对于圆柱滚刀和齿轮滚刀而言，采用唯一的砂轮轴截形即可磨削出螺旋容屑槽前刀面^[18]，但是，对于环面蜗轮滚刀而言，每个刀齿两侧的刃口曲线及其上每点在滚刀基本蜗杆齿面螺旋线上的螺旋升角都不一样，加工每个刀齿都需要采用不同轴向截形的成形砂轮，这在实际生产中是很难实现的。
本文首先提出采用双锥砂轮磨削螺旋容屑槽环面蜗轮滚刀前刀面的方法，建立由双锥产形面展成平面二次包络环面蜗轮滚刀螺旋容屑槽前刀面的数学模型，给出每个刀齿两侧在分度环面螺旋线上的前角计算公式。然后，分别计算螺旋容屑槽滚刀和直容屑槽滚刀对应的前角，对比分析螺旋容屑槽对前角的改善效果；对环面蜗轮滚刀螺旋容屑槽进行仿真加工，并且在仿真软件中对前角进行测量。最后，对比理论计算结果和仿真结果，验证环面蜗轮滚刀前刀面成形方法的正确性。
1 前刀面的数学模型 滚刀的前刀面是在滚刀基本蜗杆螺旋面的基础上开制容屑槽而得到。以平面Σ_d为产形面，一次包络滚刀基本蜗杆螺旋面Σ₁；以双锥面Σ_qd为产形面，一次包络滚刀前刀面Σ₂。
1.1 加工前刀面的坐标系及相对运动关系 建立如图 1所示的右旋直角坐标系，取静坐标系σ_qo1(O_qo1；i_qo1，j_qo1，k_qo1)与机架固连，动坐标系σ_q1(O_q1；i_q1，j_q1，k_q1)与滚刀基本蜗杆固连，O_q1为坐标原点，O_qo1和O_q1重合，k_qo1=k_q1与滚刀基本蜗杆回转轴线重合, 双锥砂轮的自身坐标系为σ_a(O; i_a; j_a; k_a)。

图 1 加工前刀面的坐标系 Fig. 1 Coordinate systems of rake face machining

图选项

取静坐标系σ_qod(O_qod；i_qod，j_qod，k_qod)与机架固连，i_qod=i_qo1，k_qod=-j_qo1。取动坐标系σ_qd(O_qd；i_qd，j_qd，k_qd)与刀座固连，k_qd=k_qod，k_qd与刀座轴线重合，刀座轴心O_qd到O点的距离为a₀，a_q= 是两静坐标系的中心距，本文中取a_q=a，a为环面蜗杆副的中心距。
由双锥产形面Σ_qd展成螺旋槽前刀面Σ₂时，刀座绕回转轴k_qod的转速为ω_qd，转角为φ_qd，滚刀基本蜗杆绕回转轴k_qo1的转速为ω_q1，转角为φ_q1。φ_q1与φ_qd成正比，即

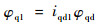(1)

式中：i_qd1为滚刀基本蜗杆与刀座的速比。当φ_q1=0时，即速比i_qd1=0，加工出直容屑槽滚刀，形成直槽滚刀的前刀面；当φ_q1≠0时，双锥产形面以一定的速比i_qd1加工出圆弧槽底的螺旋槽，形成螺旋槽滚刀的前刀面。
1.2 坐标变换 采用回转矩阵法变换坐标^[1]，例如由坐标系σ_a变换到σ_qd，表示为σ_a→σ_qd。加工滚刀前刀面时，用到坐标变换回转矩阵如下：

式中：β_a为产形锥面绕i_qd轴逆时针旋转的角度。
1.3 滚刀基本蜗杆与刀座速比i_qd1的求解 滚刀基本蜗杆齿面螺旋线喉部分度圆导程角为γ_m，前刀面螺旋线喉部分度圆导程角为γ_q，为减小每个刀齿的侧前角，保证前刀面螺旋线和齿面螺旋线在喉部分度圆处垂直，其导程角需满足

(2)

滚刀基本蜗杆齿面螺旋线喉部分度圆导程角γ_m(螺旋面右旋时为正)由式(3)求得

(3)

式中：i_1d为蜗杆毛坯和刀座的速比，其值等于蜗杆副的速比i₁₂；r₁为滚刀基本蜗杆喉部分度圆半径；r₂为滚刀分度圆弧半径。
滚刀前刀面螺旋线喉部分度圆导程角γ_q由式(4)求得

(4)

将式(3)和式(4)代入式(2)求得

(5)

1.4 滚刀基本蜗杆螺旋面的矢量表达式 加工滚刀基本蜗杆时，其毛坯与σ_q1固连，式(6)为滚刀基本蜗杆螺旋面在σ_q1中的方程^[1-2]：

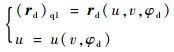(6)

展开即为

滚刀基本蜗杆螺旋面上任一点处的法矢量在σ_q1中的表达式为^[1-2]

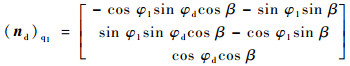(7)

式中：u和v为产形平面Σ_d的参数；r_b为蜗轮主基圆的半径；β为产形平面轴线倾角；φ_d为刀座的瞬时转角，与蜗杆毛坯的瞬时转角φ₁成正比，即φ₁=i_1dφ_d。
1.5 双锥产形面的矢量表达式 如图 2所示，展成滚刀前刀面的双锥产形面Σ_qd在砂轮中间平面的右侧。取坐标系σ_a(O；i_a，j_a，k_a)与砂轮固连；k_a与砂轮轴线重合，i_a和j_a在砂轮中间平面上。

图 2 双锥产形面 Fig. 2 Double-cone grinding surface

图选项

利用圆矢量函数和球矢量函数，右边产形锥面Σ_qd在坐标系σ_a中的矢量表达式为

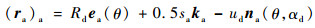(8)

式中：s_a为双锥砂轮顶宽；α_d为双锥砂轮齿形角；u_d和θ为Σ_qd的参数; e_a()为圆矢量函数；R_d为双锥砂轮半径。
右边产形锥面Σ_qd上任一点Q处的单位法矢量为

(9)

砂轮在刀座上处于图 3所示的位置时，即产形锥面绕i_qd轴逆时针旋转β_a，将式(8)依次进行σ_a→σ_qd、σ_qd→σ_qod、σ_qod→σ_qo1及σ_qo1→σ_q1的坐标变换，得到产形锥面Σ_qd在动坐标系σ_q1中的矢量表达式为

图 3 砂轮在刀座静坐标系中的位置 Fig. 3 Position of grinding wheel in tool holder's static coordinate system

图选项

(10)

式中：

将式(9)进行σ_a→σ_qd、σ_qd→σ_qod、σ_qod→σ_qo1及σ_qo1→σ_q1的坐标变换，得到右边产形锥面Σ_qd上任一点Q在动坐标系σ_q1中的单位法矢量为

(11)

式中：

本文中取：

1.6 在σ_q1中滚刀前刀面的方程 在σ_qod坐标系中，双锥产形面与前刀面的相对速度为(v_qd1)_qod，由齿轮啮合原理^[19-21]得到双锥产形面与前刀面共轭条件函数为

(12)

由Ф_qod=0得到双锥产形面的一次包络共轭条件方程为

(13)

式中：

(14)

(15)

联立式(10)和式(13)可得滚刀前刀面Σ₂在σ_q1中的方程为

(16)

1.7 前角V_q的表达式 将滚刀基本蜗杆螺旋面Σ₁的方程式(6)和前刀面Σ₂的方程式(16)联立组成方程组，即可求得滚刀刀齿的刃口线。
在σ_q1坐标系中，由刃口线上任一点在前刀面上的法向量(n_qd)_q1和在螺旋面上的法向量(n_d)_q1求得该点处的前角V_q表达式为^{[10-11, 22]}

(17)

式中：arccos[(n_qd)_q1·(n_d)_q1]为该点处的夹角W_q。
2 算例及结果分析 滚刀基本蜗杆左侧螺旋面和前刀面的交线为左侧刃口线，左侧刃口线上任一点处的前角为左侧前角，同理，右侧刃口线上任一点处的前角为右侧前角，刃口线上任一点处的前角对应滚刀的轴向位置为Z_i。本文针对表 1中提供的算例^[6]，通过改变双锥砂轮各个参数的取值来计算对应的前角，选取了一组较为合理的双锥砂轮参数。选取双锥砂轮的参数分别为：双锥砂轮半径R_d=50 mm，双锥砂轮顶宽s_a=6 mm，双锥砂轮齿形角α_d=15°，双锥砂轮轴线倾角β_a=116.5°，分别求解直槽和螺旋槽滚刀的前角。令式(1)中φ_q1=0，即速比i_qd1=0，求得对应的直槽滚刀在分度环面上从出口到入口的前角大小如表 2所示；由式(5)求得速比i_qd1=-1.54时，对应的螺旋槽滚刀在分度环面上从出口到入口的前角大小如表 3所示。
表 1 平面二次包络环面蜗轮滚刀及双锥砂轮的基本参数^[6] Table 1 Basic parameters of planar double enveloping hourglass worm gear hob and double-cone grinding wheel ^[6]

参数	数值
中心距a/mm	160
速比i12	10
滚刀头数z1	4
蜗轮分度圆压力角α/(°)	21.8667
蜗轮分度圆直径d2/mm	255
蜗杆分度圆直径d1/mm	65
滚刀齿顶圆弧半径Ra1/mm	122.24
滚刀齿根圆弧半径Rf1/mm	133.24
滚刀工作长度Lw/mm	90
滚刀喉部分度圆导程角γm/(°)	21.4205
产形平面轴线倾角β/(°)	22.5
主基圆直径db/mm	95

表选项






表 2 直槽前刀面对应分度环面上各刀齿左右两侧的前角 Table 2 Rake angles of both sides of each tooth on indexing torus corresponding to rake face of hob with straight flutes

齿号	左侧			右侧
	前角/(°)	轴向位置/mm		前角/(°)	轴向位置/mm
1号	-15.7159	-43.5		16.9998	-35.8
2号	-18.1932	-24.5		19.0122	-15.4
3号	-19.5303	-4.71		19.5304	4.71
4号	-19.0126	15.4		18.1937	24.5
5号	-17.0004	35.8		15.7165	43.5

表选项






表 3 螺旋槽前刀面对应分度环面上各刀齿左右两侧的前角 Table 3 Rake angles of both sides of each tooth on indexing torus corresponding to rake face of hob with spiral flutes

齿号	左侧			右侧
	前角/(°)	轴向位置/mm		前角/(°)	轴向位置/mm
1号	5.5645	-37.6659		-5.4788	-30.6111
2号	6.6612	-21.2130		3.0636	-13.3234
3号	7.2522	-4.1854		6.2043	3.9941
4号	1.6208	13.3526		0.7470	21.4250
5号	-1.3445	31.1470		-8.1071	38.3567

表选项






根据表 2和表 3的数据，绘制直槽滚刀和螺旋槽滚刀对应的前角变化规律，如图 4所示。

图 4 不同容屑槽两侧前角变化规律 Fig. 4 Change law of rake angles on both sides of different spiral flutes

图选项

由表 2可知，环面蜗轮滚刀的容屑槽为直槽时，刀齿分度环面上左右两侧前角近似在±20°之间。左侧为负前角，右侧为正前角。由图 4可知，左侧刀齿从出口(Z_i=-0.5L_w处)到入口(Z_i=0.5L_w处)前角的绝对值先增大后减小，喉部齿位置(3号齿)前角的绝对值最大；右侧刀齿从入口(Z_i=-0.5L_w处)到出口(Z_i=0.5L_w处)前角的绝对值先增大后减小，喉部齿位置(3号齿)前角的绝对值最大。较大的负前角会导致刀齿切削条件恶劣，甚至无法正常滚切蜗轮。刀齿左右两侧前角一正一负且相差较大，会造成两侧刀齿切削力不均衡，引起更大的刀齿磨损。
由表 3可知，环面蜗轮滚刀的容屑槽为螺旋槽时，刀齿分度环面上左右两侧前角近似在±8.1°之间。左侧为正前角，右侧为绝对值较小的负前角。由图 4可知，喉部齿位置(3号齿)前角较为均衡，左侧前角为7.252 2°，右侧前角为6.204 3°；2个边齿(1号齿和5号齿)左右两侧的前角绝对值相差较大。原因是由于滚刀基本蜗杆螺旋线的导程角从出口到入口都是变化的，本文以喉部螺旋线的导程角为依据计算的速比i_qd1。但是，相较于直槽滚刀，刀齿两侧前角绝对值有明显下降，降幅约为60%。左侧负前角的一侧切削条件能够得到改善，而且有利于均衡刀齿左右两侧的切削条件。
3 VERICUT加工滚刀螺旋槽 以表 1中的4头滚刀为例，在VERICUT软件中建立具有B轴和C轴联动的环面蜗杆专用数控机床^[23-24]，进行滚刀基本蜗杆螺旋面以及滚刀螺旋容屑槽的仿真加工。仿真加工滚刀基本蜗杆螺旋面和螺旋容屑槽的过程如图 5所示。

图 5 仿真加工滚刀过程 Fig. 5 Simulation of processing hob process

图选项

螺旋容屑槽滚刀仿真加工完成后，测量分度环面上刀齿两侧的夹角W_q，如图 6所示。

图 6 测量分度环面上刀齿两侧的夹角 Fig. 6 Measured angle between sides of the teeth on indexing tours

图选项

由V_q=W_q-90°，计算出刀齿两侧的前角V_q，如表 4所示。
表 4 测量螺旋槽前刀面对应分度环面上各刀齿左右两侧的前角 Table 4 Measured rake angles of both sides of each tooth on indexing torus corresponding to rake face of hob with spiral flutes

齿号	左侧			右侧
	前角/(°)	轴向位置/mm		前角/(°)	轴向位置/mm
1号	5.6286	-37.6659		-5.3759	-30.6111
2号	6.3011	-21.2130		2.5098	-13.3234
3号	7.1336	-4.1854		5.6398	3.9941
4号	1.6094	13.3526		0.1771	21.4250
5号	-1.0385	31.1470		-8.3156	38.3567

表选项






将表 4测量结果和表 3中理论计算结果对比可知，测量结果是有误差的，最大误差出现在4号齿的右侧前角，为0.569 9°；最小误差出现在4号齿的左侧前角，为0.011 4°；测量误差主要是由测量点选取位置的误差造成的。
4 结论 1) 针对直槽滚刀负前角绝对值较大、刀齿左右两侧切削条件不均衡的问题，提出了采用双锥砂轮磨削加工环面蜗轮滚刀螺旋槽前刀面的方法。
2) 通过建立磨削加工坐标系，推导由双锥产形面展成平面二次包络环面蜗轮滚刀螺旋容屑槽前刀面的数学模型，完成每个刀齿在分度环面螺旋线上的前角数值的计算。计算结果表明，相较于直容屑槽滚刀，螺旋容屑槽滚刀对应的前角下降了60%，有效减小了负前角的绝对值，有利于均衡刀齿两侧的切削条件。
3) 对滚刀的螺旋容屑槽进行仿真加工并且在仿真软件中对前角进行测量，测量结果与理论计算误差小于0.6°，验证了本文方法的正确性。
致谢 感谢中南大学高性能复杂制造国家重点实验室对VERICUT软件提供的技术支持。

参考文献

[1]	董学朱. 环面蜗杆传动设计和修形[M]. 北京: 机械工业出版社, 2004: 14-15. DONG X Z. Design and modification of enveloping worm gearing[M]. Beijing: Mechanical Industry Press, 2004: 14-15. (in Chinese)
[2]	罗文军, 陈永洪, 张光辉. 平面包络环面蜗杆齿面的螺旋线误差检测及溯源[J]. 西南交通大学学报, 2015, 50(2): 279-285. LUO W J, CHEN Y H, ZHANG G H. Helix error testing and tracing on planar enveloping hourglass worm tooth surface[J]. Journal of Southwest Jiaotong University, 2015, 50(2): 279-285. DOI:10.3969/j.issn.0258-2724.2015.02.011 (in Chinese)
[3]	郝建军, 张光辉, 施全. 环面蜗轮滚刀可重磨性研究与应用——环面蜗轮滚刀理论分析[J]. 重庆理工大学学报(自然科学版), 2010, 24(6): 23-28. HAO J J, ZHANG G H, SHI Q. Research and application on annular worm gear hob rlieving grinding-Annular worm gear hob theory[J]. Journal of Chongqing University of Technology (Natural Science Edition), 2010, 24(6): 23-28. DOI:10.3969/j.issn.1674-8425-B.2010.06.006 (in Chinese)
[4]	唐建生. 金属切削与刀具[M]. 武汉: 武汉理工大学出版社, 2009: 188-189. TANG J S. Cutting and cutting tools[M]. Wuhan: Wuhan University of Technology Press, 2009: 188-189. (in Chinese)
[5]	ZHAO Y P, SU D Z, ZHANG Z. Meshing analysis and technological parameters selection of dual tori double-enveloping toroidal worm drive[J]. Mechanism and Machine Theory, 2010, 45(9): 1269-1285. DOI:10.1016/j.mechmachtheory.2010.04.004
[6]	周良墉. 环面蜗杆修型原理及制造技术[M]. 长沙: 国防科技大学出版社, 2005: 558-559. ZHOU L Y. The modification principle and manufacturing technology of hourglass worm[M]. Changsha: National University of Defense Technology Press, 2005: 558-559. (in Chinese)
[7]	董李扬.包络环面蜗杆副蜗轮滚刀数控加工技术的研究[D].北京: 中国农业大学, 2013: 15-20. DONG L Y.Research on NC machining technology of enveloping worm gear hob[D].Beijing: China Agricultural University, 2013: 15-20(in Chinese).
[8]	柳冠伊.包络环面蜗轮滚刀数控成形理论及技术研究[D].北京: 中国农业大学, 2016: 13-14. LIU G Y.Research on CNC relief grinding technology of enveloping worm gear hob[D].Beijing: China Agricultural University, 2016: 13-14(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10019-1016085319.htm
[9]	YANG J, LI H T, RUI C J.Research on a generating method of spiral flutes of hourglass worm gear hob[C]//Proceedings of the ASME Design Engineering Technical Conference.NewYork: ASME, 2017: 10.
[10]	杨杰, 李海涛, 芮成杰, 等. 环面蜗轮滚刀螺旋槽前刀面设计及修正方法[J]. 北京航空航天大学学报, 2008, 44(9): 1878-1887. YANG J, LI H T, RUI C J, et al. Design and correct method of spiral flutes rake face of an hourglass worm gear hob[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 44(9): 1878-1887. (in Chinese)
[11]	YANG J, LI H T, RUI C J, et al. A method to generate the spiral flutes of an hourglass worm gear hob[J]. International Journal of Mechanical Design, 2018, 140(6): 063301. DOI:10.1115/1.4039769
[12]	GUNAY M. Investigation of the effect of rake angle on main cutting force[J]. International Journal of Machine Tools & Manufacture, 2004, 44(9): 953-959.
[13]	GUNAY M. Experimental investigation of the effect of cutting tool rake angle on main cutting force[J]. Journal of Materials Processing Technology, 2005, 166(1): 44-49. DOI:10.1016/j.jmatprotec.2004.07.092
[14]	SAGLAM H, UNSACAR F, YALDIZ S. Investigation of the effect of rake angle and approaching angle on main cutting force and tool tip temperature[J]. International Journal of Machine Tools and Manufacture, 2006, 46(2): 132-141. DOI:10.1016/j.ijmachtools.2005.05.002
[15]	CHANG S L. Helix gash of hob cutter manufactured by milling[J]. Journal of Materials Processing Technology, 2003, 142(2): 569-575. DOI:10.1016/S0924-0136(03)00661-7
[16]	舒勤业.双锥面二次包络环面蜗杆副及其关键制造装备的设计与研究[D].杭州: 浙江大学, 2015: 21-30. SHU Q Y.Design and research of dual-cone double enveloping hourglass worm gear pair and its key manufacturing equipment[D].Hangzhou: Zhejiang University, 2015: 21-30(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10335-1015630213.htm
[17]	刘杰华. 大螺旋槽零前角滚刀前刀面重磨时砂轮廓形的修整计算[J]. 磨床与磨削, 1996(4): 25-26. LIU J H. Dressing calculation of the profile of the grinding wheel on the rake face of the hob with zero rake angle[J]. Grinding Machine and Grinding, 1996(4): 25-26. (in Chinese)
[18]	陈就, 刘丰林, 康权. 一种滚刀径向铲磨优化方法[J]. 中国机械工程, 2014, 25(14): 1883-1887. CHEN J, LIU F L, KANG Q. An optimization method for hob relief grinding[J]. China Mechanical Engineering, 2014, 25(14): 1883-1887. DOI:10.3969/j.issn.1004-132X.2014.14.008 (in Chinese)
[19]	LITVIN F L. Theory of gearing[M]. Washington, D.C.: NASA Reference Publication, 1989: 57-62.
[20]	董学朱. 齿轮啮合理论基础[M]. 北京: 机械工业出版社, 1989: 90-92. DONG X Z. Gear meshing theory[M]. Beijing: China Machine Press, 1989: 90-92. (in Chinese)
[21]	吴序堂. 齿轮啮合理论[M]. 2版. 西安: 西安交通大学出版社, 2009: 104-110. WU X T. Gear meshing theory[M]. 2nd ed. Xi'an: Xi'an Jiao Tong University Press, 2009: 104-110. (in Chinese)
[22]	姜正健, 张伟, 李铸宇. 微钻的前角计算及其钻削试验[J]. 大连工业大学学报, 2011, 30(2): 145-147. JIANG Z J, ZHANG W, LI Z Y. Calculation of the rake angle of micro drill and drilling test[J]. Journal of Dalian Institute of Light Industry, 2011, 30(2): 145-147. DOI:10.3969/j.issn.1674-1404.2011.02.019 (in Chinese)
[23]	LIU G Y, WEI W J, DONG X Z, et al. Relief grinding of planar double-enveloping worm gear hob using a four-axis CNC grinding machine[J]. The International Journal of Advanced Manufacturing Technology, 2016, 89(9-12): 3631-3640.
[24]	杨胜群, 唐秀梅. VERICUT数控加工仿真技术[M]. 北京: 清华大学出版社, 2010: 77-81. YANG S Q, TANG X M. VERICUT NC machining simulation technology[M]. Beijing: Tsinghua University Press, 2010: 77-81. (in Chinese)