针对飞轮的故障诊断主要有2类方法[2],包括基于解析模型的方法和基于知识的方法。基于解析模型的方法包括观测器[3-4]和滤波器[5-6]。这一类方法需要建立系统的数学模型,模型精度决定故障诊断效果,因此这种方法限制条件较多,可移植性差。基于知识的方法包括神经网络[7-8]和支持向量机[9-10]。这一类方法无需建立系统的精确数学模型,通过历史数据的训练能够得到足够精度的拟合模型,因此该方法具有学习能力,但是其参数调整十分复杂,且模型的可解释性差。为了避免复杂的数学建模,文献[11-13]基于数据驱动实现了飞轮的故障诊断,但是也存在计算复杂、数据量要求高等不足。
混沌性是一种广泛存在于非线性系统中的特性[14],相空间重构理论[15]表明可以利用较少的变量刻画复杂系统的特性,因此混沌性可以作为系统特征用于故障诊断。基于混沌的故障诊断在电力、机械领域已经取得了应用[16-17],在航天领域亦有少量研究[18-19],具有对微弱故障的敏感性和噪声的免疫力。
对于飞轮这一类物理模型复杂的非线性系统,本文提出一种数据驱动的故障检测方法;由于飞轮的混沌性在控制算法的作用下不显著,构造一个由飞轮参数和辅助函数组成的离散动力系统,该系统可以稳定地产生混沌吸引子;利用混沌吸引子形态在故障情况下的变化检测故障。
1 飞轮模型 根据文献[20]给出的ITHACO-A型反作用飞轮的高精度数学模型,建立了基于Simulink的飞轮高精度仿真模型,如图 1所示。
 |
| 图 1 高精度飞轮仿真模型 Fig. 1 High-accuracy simulation model of flywheel |
| 图选项 |
图 1中相关参数如下:Vc为等效控制电压;τz为输出力矩;Vbus为母线电压;ω为飞轮转速;ωd为驱动带宽;Im为电机电流;Ibus为母线电流;B、C为常数;Hb、Hf和Hz均为Heaviside step函数;参考文献[13]设置仿真参数,具体取值见表 1。
表 1 飞轮仿真模型参数设置 Table 1 Parameter setting of flywheel simulation model
| 参数 | 数值 |
| 驱动增益Gd/(A·V-1) | 1 |
| 电机转动系数Kt/(N·m·A-1) | 0.19 |
| 电机电动势反馈系数Ke/(V·rad-1·s-1) | 0.29 |
| 转速限制增益系数Ks/(V·rad-1·s-1) | 95 |
| 转速限制阈值ωs/ (r·min-1) | 690 |
| 静摩擦力矩τc/(N·m) | 0.002 |
| 飞轮转动惯量J/(N·m·s2) | 0.078 |
| 电机磁极数量Np | 36 |
| 滑动摩擦力矩τv/(N·m·s·rad-1) | 0.037 |
| 输入电阻Rin/Ω | 2 |
| 力矩噪声引起的角误差θα/rad | 0.05 |
| 高通噪声滤波器频率ωα/(rad·s-1) | 0.2 |
| 电压反馈增益kf | 0.5 |
表选项
飞轮的常见故障模式有:卡死故障、空转故障、摩擦增大故障、增益下降故障和跳变故障。按照故障随时间的变化可分为突变故障和缓变故障2种。缓变故障在早期通常会表现为幅度较小的性能变化,其中摩擦增大故障和增益下降故障是较常见的早期故障。摩擦增大故障主要表现为飞轮的输出力矩与期望控制力矩差异增大,其故障模型可等效为各类摩擦系数变大;增益下降故障主要表现为飞轮输出力矩相对期望控制力矩比例减小,其故障模型可等效为电机驱动增益Gd减小。
根据图 1建立的飞轮模型可以得到如下的飞轮状态空间模型:
 | (1) |
式中:Vvc为飞轮输入的控制电压;ψ1(Im, ω)、ψ2(ω)和ψ3(ω)分别为电动势力矩限制、轴承摩擦力与力矩干扰和电机转速限制这3个非线性过程。式(1)反映了电机电流是表征系统的重要变量,系统状态的改变必然伴随着电机电流的变化,因此本文选用电机电流Im作为分析的变量。
2 故障检测方法 基于混沌的故障检测方法通常利用参数时间序列自身的混沌特征进行检测,如最大Lyapunov指数、分形维数、盒维数等。该方法的前提条件是待检测系统处于混沌状态。飞轮系统由于处在控制算法作用之下,其混沌特性被抑制,并不能总是处在混沌状态中,因此通常的基于混沌的故障检测方法不适用于飞轮系统的故障检测。本文采取构造混沌离散动力系统的方法进行飞轮系统的故障检测。
2.1 离散动力系统的构造方法 以第1节所述模型进行混沌性分析,当飞轮保持在任意稳定工况下时,计算Im不同时间数据序列的最大Lyapunov指数λ,结果见图 2,n为采样点数。其值并不总是正的,即飞轮系统的混沌性不是稳定出现的,也意味着不能直接使用系统的混沌特性。因此需要构造一个存在稳定的混沌特性的系统。
 |
| 图 2 Im的最大Lyapunov指数 Fig. 2 The largest Lyapunov exponent of Im |
| 图选项 |
能够产生混沌的动力系统模型有很多,常见的如Lorenz系统、Logistic系统和Henon系统等。但是将飞轮系统的数学模型变换为类似的混沌系统形式是比较困难的,因此考虑其他形式的构造方法。文献[21]的研究表明对于图像函数而言,存在满足一定条件的辅助函数使得构成的离散动力系统出现混沌吸引子。基于这一结论构造如下离散动力系统:
 | (2) |
式中:k为正弦曲面函数参数;相空间重构灰度图像g(x, y)由待分析变量Im经过相空间重构生成;f(x, y)和g(x, y)的定义域与值域应调整一致。选择该辅助函数的原因是在参数k的控制下能够形成不同振荡程度、不同梯度以及充满整个定义域的曲面,这样的辅助曲面更容易产生混沌。
2.2 离散动力系统参数的选择 构造g(x, y)有2个目的:一是使其符合灰度图像函数的特点;二是能反映原数据序列的特征。相空间重构理论证明了存在一个合适的嵌入维m,如果满足m>2d+1,d为动力系统的维数,那么在这个m维的相空间中可以恢复出原系统的吸引子。通过选择不同的嵌入维m和时延τ组合,可以生成不同大小的相空间矩阵,对应不同尺寸的灰度图像函数。因此采用相空间重构法生成所需函数。
对于一个单变量时间序列{xi},如果嵌入维和时延为m和τ,则可按如式(3)形式构造相空间[15]:
 | (3) |
式中:i=1,2,…,L;L=N-(m-1)τ,N为序列长度。
对于一般的系统而言,不失一般性的,时延τ通常可以选择为1或者2,具有简单性、比较强的可操作性和实用性。嵌入维m的选择需要考虑灰度图像的特点,本文选择2的幂数256、128或64等。不同维数对结果的影响会在3.3节予以讨论。
为确保构造离散动力系统能够大概率的产生混沌吸引子,需要选择合适的辅助函数f(x, y)参数k。为此给出了在m=256的条件下,参数k变化下的分岔图和系统最大Lyapunov指数图,分别如图 3和图 4所示。
 |
| 图 3 离散动力系统的分岔图 Fig. 3 Bifurcation diagram of discrete dynamic system |
| 图选项 |
 |
| 图 4 离散动力系统的最大Lyapunov指数 Fig. 4 The largest Lyapunov exponent of discrete dynamic system |
| 图选项 |
如图 3所示,当参数k大于3时,系统进入混沌状态。对比图 4,在同样的k值下绝大部分最大Lyapunov指数为正,证明了在这一k值区间中系统会产生混沌吸引子。
2.3 基于混沌吸引子的故障检测原理分析 混沌系统具有以下性质:对初值敏感性、有界性、遍历性、内随机性和分维性等。主要利用前3种性质进行故障检测。混沌系统对初值敏感性表明,对于一个混沌系统,不同的初值会产生不同的响应;有界性表明系统的运动轨迹始终局限在一个确定的区域内;遍历性表明系统运动轨迹在吸引域内是各态遍历的。
由于混沌吸引子的有界性和遍历性,使用2.1与2.2节构造的离散动力系统生成近似吸引子时只要迭代次数足够,则无论选择哪个初始点,最终的吸引子形状是一致的。图 5(a)为初始点(65,90)开始迭代300次后的吸引子,图 5(b)为初始点(90,65)开始迭代300次后的吸引子,二者形状基本一致。
 |
| 图 5 初始点(65, 90)和(90,65)的混沌吸引子 Fig. 5 Chaotic attractor with initial points (65, 90) and (90, 65) |
| 图选项 |
当飞轮系统发生故障时,参数变化规律发生改变,构造的离散动力系统特性也随之改变,于是迭代生成的混沌吸引子形状发生变化。图 6为30%幅度的飞轮电机增益变小故障下吸引子图像,与图 5(a)和图 5(b)相比吸引子的形状变化显著。利用这一变化可以进行故障检测。
 |
| 图 6 初始点(65, 90),Kgd=0.7时的混沌吸引子 Fig. 6 Chaotic attractor with initial point (65, 90) and Kgd=0.7 |
| 图选项 |
为利用混沌吸引子的变化进行故障检测,需要提取描述混沌吸引子的特征。本文构造产生的混沌吸引子实际是一个二位平面函数,因此可以采用rodon变换将其映射为一维数组,通过对变换后的一维数组进行多项式拟合,即可得到混沌吸引子的特征多项式。正常情况下的混沌吸引子特征应是近似相同的,而故障情况下的混沌吸引子特征与正常情况应有较大区别,因此计算不同混沌吸引子特征多项式的相关系数进行故障检测。
混沌系统对初值的敏感性使得基于混沌吸引子的故障检测方法对故障十分敏感,这一点会在3.2节的仿真中进行验证。
2.4 基于混沌吸引子的故障检测方法流程 2.3节的分析中论述了混沌吸引子与故障间的关系,以此为依据设计如下的故障检测方法:
1) 数据预处理。按所需的灰度图像尺寸采集相应长度的数据序列,对采集到的数据进行归一化处理使数据分布在[0, 1]区间内,将数据值转换为灰度值。
2) 生成混沌吸引子。随机选择初始点,以构造的离散动力系统进行一定次数的迭代计算生成混沌吸引子。
3) 计算混沌吸引子特征。对生成的混沌吸引子矩阵进行radon变换,对变换后的数据进行拟合,以拟合的多项式生成固定长度的特征向量。
4) 故障检测。选取平稳工况下的混沌吸引子作为标准,计算待检测序列的混沌吸引子与其相关系数,相关系数低于阈值则认为检测到故障的发生。
3 数值仿真分析 3.1 闭环飞轮仿真系统 在文献[13]的仿真条件基础上,增加了不同工况下的故障检测仿真。搭建的闭环飞轮仿真系统如图 7所示。
 |
| 图 7 闭环飞轮控制系统框图 Fig. 7 Block diagram of flywheel with closed-loop control system |
| 图选项 |
该闭环飞轮控制系统为速度反馈控制系统,包含PID控制器、飞轮模型和数据采集系统。PID控制器参数设置为:比例系数KP为0.1,积分系数KI为0.05, 微分系数KD为0.1。飞轮模型参数按表 1所示设置。设置电机增益变小故障系数为Kgd∈(0, 1],摩擦力矩增大故障系数为Kτ∈[1, +∞),则有

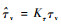
 | (4) |
考虑实际的姿态控制系统仅少部分时间处在大角度机动状态下,大部分时间为稳定姿态,修正空间干扰力矩以及轨道转速的影响,因此本文指定的飞轮工作状态为抵抗空间干扰力矩作用下的姿态保持过程,设置目标转速为常值叠加干扰力矩对应的速度变化:
 | (5) |
式中:ωc=4.5 rad/s;ω0=0.02 rad/s;A=0.14。
设置3种测量噪声条件,信噪比分别为75 dB(标称)、55 dB(中等强度)和45 dB(高强度), 其中“标称”噪声是指目前器件的典型噪声水平。设置了电机增益变小和摩擦力矩增大2种故障。每种噪声条件下2种故障各有6组数据,其中1组为正常数据;5组为故障数据。设置电机增益变小故障系数Kgd分别为0.7、0.82、0.91、0.94和0.97,即故障参数的偏差幅度分别为正常值的30%、18%、9%、6%和3%;摩擦力矩故障系数Kτ分别为1.3、1.21、1.09、1.06和1.03,即故障参数的偏差幅度分别为正常值的30%、18%、9%、6%和3%。
故障检测的阈值根据正常数据产生的混沌吸引子相似度选取,可以选择最大值或是平均值,本文选取最大值为阈值。
系统仿真长度为400 s,步长为0.01 s,设置故障时刻为200 s,单次仿真共40 000点数据。仿真过程中电流和飞轮转速初值均为零。采用的分析量为电机电流Im,由于系统初始时刻有一个调节过程,因此本文只从50 s后的稳态开始进行分析,即每次仿真采用50~400 s间的数据,共35 000个采样点。
3.2 飞轮系统的故障检测
3.2.1 电机增益变小故障 标称噪声(75 dB)条件下的5段故障数据均为50~400 s间的采样点,每段为35 000个采样点,如图 8所示。微小幅度下的故障与正常数据的偏差很小,基本掩盖在了噪声范围内,当故障幅度逐渐增大时,故障数据与正常数据有了明显的偏差,但是经过一段时间后,在反馈控制的作用下系统重新恢复稳定。
 |
| 图 8 飞轮电机增益变小故障的电机电流 Fig. 8 Current of flywheel under fault of motor gain decrease |
| 图选项 |
按2.4节所述方法对采集的数据进行计算,其中辅助函数参数k取值为3.141 6,嵌入维m取值为256。
标称噪声(75 dB)条件下不同故障幅度的检测结果如图 9所示,kre为相差系数。随着故障幅值的增大,其与正常数据的相似度越来越低,以0.8为阈值的情况下,对3%幅度(即Kgd=0.97)的故障依然响应灵敏,该方法对电机增益变大故障很敏感。同时,由于控制目标的波动,图 9也表明了飞轮系统的平稳状态特征与电机增益故障特征是与控制目标的幅值无关,因此该方法可以应用在不同控制目标的条件下。
 |
| 图 9 75 dB噪声下电机增益变小故障检测结果 Fig. 9 Fault detection result of motor gain decrease under 75 dB noise |
| 图选项 |
考察本文方法对噪声的鲁棒性,以3种噪声条件下故障系数Kgd=0.7的故障检测为例,检测结果如图 10所示。相同的故障在不同噪声条件下的检测效果是一致的,证明本文方法对噪声具有鲁棒性。
 |
| 图 10 不同噪声条件下电机增益变小故障检测结果(Kgd=0.7) Fig. 10 Fault detection result of motor gain decrease under different noises (Kgd=0.7) |
| 图选项 |
3.2.2 摩擦力矩增大故障 标称噪声(75 dB)条件下的5段故障数据均为50~400 s间的采样点,每段为35 000个采样点。如图 11所示,微小幅度下的故障与正常数据的偏差很小,大部分处在噪声范围内,当故障幅度逐渐增大时,故障数据与正常数据有了明显的偏差,由于摩擦力增大故障是通过转速间接影响电机电流的,因此在经过一段时间后,在反馈控制的作用下系统重新恢复稳定时的电流值会变大。
 |
| 图 11 摩擦力矩增大故障的的电机电流 Fig. 11 Current of motor in fault of motor friction moment increase |
| 图选项 |
按2.4节所述方法对采集的数据进行计算,其中辅助函数参数k取值为3.141 6,嵌入维m取值为256。
标称噪声(75 dB)条件下不同故障幅度的检测结果如图 12所示。在阈值为0.8时能够检出9%幅度(即Kτ=1.09)的故障,但对于更小幅度故障的检测区分度不如电机增益变大故障的检测明显。同时,由于控制目标的波动,图 12也表明了飞轮系统的平稳状态特征与电机增益故障特征是与控制目标的幅值无关,因此该方法可以应用在不同控制目标的条件下。
 |
| 图 12 75 dB噪声下摩擦力矩增大故障检测结果 Fig. 12 Fault detection result of motor friction moment increase under 75 dB noise |
| 图选项 |
考察本文方法对噪声的鲁棒性,以3种噪声条件下故障系数Kτ=1.3的故障检测为例,检测结果如图 13所示。相同的故障在不同噪声条件下的检测效果是一致的,证明本文方法对噪声具有鲁棒性。但是与电机增益故障相比,摩擦力矩故障对噪声更敏感。
 |
| 图 13 不同噪声条件下摩擦力矩增大故障检测结果(Kτ=1.3) Fig. 13 Fault detection result of motor friction moment increase under different noises (Kτ=1.3) |
| 图选项 |
3.3 嵌入维对故障检测能力的影响 以上仿真选择的嵌入维均为256,这是因为通常灰度图像都具有256个级别的灰度值,在256×256的尺寸上无需调整灰度值,方便构造混沌吸引子。但是这样对数据长度的要求相对较高,需要766长度的数据。下面讨论不同嵌入维对检测效果的影响。
为方便计算,选择的嵌入维分别为256、128、64和32;所需的数据长度分别为766、382、190和94。以标称噪声(75 dB)条件下电机增益故障和摩擦力矩故障为例进行分析,电机增益故障系数Kgd为0.91和0.7;摩擦力矩故障系数Kτ为1.09和1.3。结果如图 14所示。
 |
| 图 14 不同m下电机摩擦力矩增大故障检测结果 Fig. 14 Fault detection result of motor friction moment increase with different m |
| 图选项 |
图 14(a)、(c)的结果显示,随着嵌入维数的减小,该检测方法对故障的敏感度上升,当嵌入维为64时,对于幅度为9%的微小故障识别能力显著,当嵌入维为32时噪声的干扰掩盖了故障。图 14(b)、(d)的结果则显示,对与故障幅度较大的故障,合理的嵌入维对检测结果影响不大,但是检测窗口会随着嵌入维的减小而减小。
本文认为导致如上结果的原因是因为随着嵌入维的减小,所采集的数据长度也减小,当故障发生时,采集的数据长度越小,则数据间的相对变化就越剧烈,如图 15所示,嵌入维越大,则故障发生后电流的均值

 |
| 图 15 不同m下电机故障电流均值 Fig. 15 Mean of fault motor current under different m |
| 图选项 |
4 结论 1) 仿真结果表明基于混沌吸引子的故障检测方法能够很好地检测出3%幅度的电机增益故障和9%幅度的摩擦力矩故障,由于缓变故障在早期通常会表现为幅度较小的性能变化,因此该方法可以用于飞轮的早期故障检测。
2) 飞轮系统的数据使用曲面迭代的方法可以产生混沌吸引子,且该吸引子与迭代初始点无关;故障情况下的混沌吸引子形状会产生明显的改变。
3) 基于混沌吸引子的故障检测方法无需对系统进行精确建模,只需要健康数据即可进行故障检测,同时计算过程大部分为迭代计算,计算量小,适合用于实时故障检测。
4) 嵌入维数会影响方法对故障的敏感度和检测窗口。随着嵌入维数的减小,方法需要的数据减少,对故障的敏感程度增加,但易受噪声干扰。
5) 基于混沌吸引子的故障检测方法是一种基于数据的方法,可移植性强,可以推广应用到航天器其他系统、部件的故障检测。
参考文献
| [1] | 肇刚, 李泽, 李言俊. 基于TSEOPM的在轨航天器故障预报方法研究[J].计算机测量与控制, 2009, 17(12): 2352–2354. ZHAO G, LI Z, LI Y J. Research on method of fault prediction for onboard spacecrafts based on times series event omen pattern mining[J].Computer Meassurement & Control, 2009, 17(12): 2352–2354.(in Chinese) |
| [2] | 苏林, 尚朝轩, 刘文静. 航天器姿态控制系统故障诊断方法概述[J].长春理工大学学报(自然科学版), 2010, 33(4): 23–27. SU L, SHANG C X, LIU W J. Survey on the technology of fault diagnosis for spacecraft attitude control system[J].Journal of Changchun University of Science and Technology(Natural Science Edition), 2010, 33(4): 23–27.DOI:10.3969/j.issn.1672-9870.2010.04.006(in Chinese) |
| [3] | GAO C, DUAN G R. Robust adaptive fault estimation for a class of nonlinear systems subject to multiplicative faults[J].Circuits, Systems, and Signal Processing, 2012, 31(6): 2035–2046.DOI:10.1007/s00034-012-9434-x |
| [4] | 管宇, 张迎春, 沈毅, 等. 基于迭代学习观测器的卫星姿态控制系统的鲁棒容错控制[J].宇航学报, 2012, 33(8): 1080–1086. GUAN Y, ZHANG Y C, SHEN Y, et al. Robust fault-tolerant control for satellite attitude control system based on iterative learning observer[J].Journal of Astronautics, 2012, 33(8): 1080–1086.DOI:10.3873/j.issn.1000-1328.2012.08.012(in Chinese) |
| [5] | 李知周, 张锐, 朱振才, 等. 基于扩展卡尔曼滤波的动量轮故障检测方法[J].航空学报, 2010, 31(8): 1614–1621. LI Z Z, ZHANG R, ZHU Z C, et al. Extended Kalman filter-based fault detection for momentum wheel[J].Acta Aeronautica et Astronautica Sinica, 2010, 31(8): 1614–1621.(in Chinese) |
| [6] | AZIZI S M, KHORASANI K.Adistributed Kalman filter for actuator fault estimation of deep space formation flying satellites[C]//Proceedings of 20093rd Annual IEEE Systems Conference.Piscataway, NJ: IEEE Press, 2009: 354-359.https://www.mendeley.com/research-papers/distributed-kalman-filter-actuator-fault-estimation-deep-space-formation-flying-satellites/ |
| [7] | TALEBI H A, KHORASANI K. A neural network-based multiplicative actuator fault detection and isolation of nonlinear systems[J].IEEE Transactions on Control Systems Technology, 2013, 21(3): 842–851.DOI:10.1109/TCST.2012.2186634 |
| [8] | SHEN Q K, JIANG B, SHI P. Novel neural networks-based fault tolerant control scheme with fault alarm[J].IEEE Transactions on Cybernetics, 2014, 44(11): 2190–2201.DOI:10.1109/TCYB.2014.2303131 |
| [9] | 高运广, 王仕成, 刘志国, 等. 一种基于LS-SVM的联邦滤波故障检测方法[J].控制与决策, 2011, 26(9): 1433–1440. GAO Y G, WANG S C, LIU Z G, et al. Fault detection method based on LS-SVM for federated Kalman filter[J].Control and Decision, 2011, 26(9): 1433–1440.(in Chinese) |
| [10] | 陈冰, 鲁刚, 房红征, 等. 基于最小二乘支持向量机的卫星异常检测方法[J].计算机测量与控制, 2014, 22(3): 690–696. CHEN B, LU G, FANG H Z, et al. Method of satellite anomaly detection based on least squares support vector machine[J].Computer Measurement & Control, 2014, 22(3): 690–696.DOI:10.3969/j.issn.1671-4598.2014.03.014(in Chinese) |
| [11] | 王日新, 龚学兵, 许敏强, 等. 飞轮系统的符号动力学故障检测方法[J].哈尔滨工业大学学报, 2016, 48(10): 31–38. WANG R X, GONG X B, XU M Q, et al. A symbolic dynamic analysis of flywheel system for fault detection[J].Journal of Harbin Institute of Technology, 2016, 48(10): 31–38.DOI:10.11918/j.issn.0367-6234.2016.10.004(in Chinese) |
| [12] | 龚学兵, 王日新, 许敏强. 飞轮传感器的高斯混合模型故障检测方法[J].宇航学报, 2015, 36(6): 699–705. GONG X B, WANG R X, XU M Q. Gaussian mixed model-based fault detection method for flywheel sensor[J].Journal of Astronautics, 2015, 36(6): 699–705.DOI:10.3873/j.issn.1000-1328.2015.06.011(in Chinese) |
| [13] | 龚学兵, 王日新, 许敏强. 基于数据关联性分析的飞轮异常检测[J].航空学报, 2015, 36(3): 898–906. GONG X B, WANG R X, XU M Q. Abnormality detection for flywheel based on data association analysis[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 898–906.(in Chinese) |
| [14] | ZHANG X D, LIU X D, ZHENG Y. Chaotic dynamic behavior analysis and control for a financial risk system[J].Chinese Physics B, 2013, 22(3): 260–265. |
| [15] | TAKENS F. Detecting strange attractors in turbulence[J].Lecture Notes in Mathmatics, 1981, 898: 361–381. |
| [16] | 孙自强, 陈长征, 谷艳玲, 等. 基于混沌和取样积分技术的大型风电增速箱早期故障诊断[J].振动与冲击, 2013, 32(9): 113–117. SUN Z Q, CHEN C Z, GU Y L, et al. Incipient fault diagnosis of large scale wind turbine gearbox based on chaos theory and sampling integral technology[J].Journal of Vibration and Shock, 2013, 32(9): 113–117.DOI:10.3969/j.issn.1000-3835.2013.09.022(in Chinese) |
| [17] | 翁鹤, 皮德常. 混沌RBF神经网络异常检测算法[J].计算机技术与发展, 2014, 24(7): 29–33. WENG H, PI D C. Chaotic RBF neural network anomaly deection algorithm[J].Computer Technology and Development, 2014, 24(7): 29–33.(in Chinese) |
| [18] | 高瑞乾, 甘新年, 闫源江. 基于混沌特征的航空发动机故障诊断研究[J].国外电子测量技术, 2011, 30(3): 24–28. GAO R Q, GAN X N, YAN Y J. Study on aero-engine fault diagnosis based on chaotic feature[J].Foreign Electronic Measurement Technology, 2011, 30(3): 24–28.DOI:10.3969/j.issn.1002-8978.2011.03.007(in Chinese) |
| [19] | 侯胜利, 胡金海, 李应红. 基于混沌变量的航空发动机性能监控与故障诊断[J].航空动力学报, 2005, 20(2): 314–317. HOU S L, HU J H, LI Y H. Aeroengine performance monitoring and fault diagnosis based on chaos variable[J].Journal of Aerospace Power, 2005, 20(2): 314–317.DOI:10.3969/j.issn.1000-8055.2005.02.028(in Chinese) |
| [20] | BIALKE B. High fidelity mathematical modeling of reaction wheel performance[J].Advances in the Astronautical Sciences, 1998, 98: 483–496. |
| [21] | 于万波, 赵斌. 曲面迭代混沌特性研究[J].物理学报, 2014, 63(12): 120502. YU W B, ZHAO B. A new chaotic attractor graphics drawing method based on the curved iteration[J].Acta Physica Sinica, 2014, 63(12): 120502.DOI:10.7498/aps.63.120502(in Chinese) |
