杂凑函数(hash function)是一种单向密码体制，可以将任意长度的输入经变换后得到固定长度的输出。由于具有单向性、抗碰撞性及运算速度快等优势，杂凑函数被广泛应用于数据完整性认证、数字签名及嵌入式安全检测等领域^[1]。嵌入式系统与传统的台式机和高性能计算机相比，在运算能力、内存及能耗等方面有着严格的限制。以一个典型嵌入式系统射频识别(Radio Frequency Identification，RFID)标签为例，该系统有1 000~10 000 GE(Gate Equivalents，等效门数，表示独立于制造技术的数字电路复杂性的度量单元)，其中仅有20%左右可用于信息安全组件^[2]，而传统的杂凑函数，如MD5(8 400 GE)^[3]、SHA-1(5 527 GE)^[4]及SHA-2(10 868 GE)^[5]显然不能满足一般嵌入式系统对于安全组件的要求，在这种情况下, 轻量级杂凑函数应运而生。
与传统Merkle-Damgard结构相比，海绵结构对于长消息攻击和随机预言机区分攻击有着非常好的可证明安全性，同时在低功耗设备的实现上能节约大量内存开销，因此，近年来出现了一种采用海绵结构设计轻量级杂凑函数的新趋势。文献[6]提出了一种以海绵结构为整体，内部置换结构采用流密码Grain^[7]及分组密码KATAN^[8]的轻量级杂凑函数族QUARK，其中包括U-Quark、D-Quark和S-Quark 3个版本以适应应用系统的不同需求。在安全性方面，QUARK可提供从64 bit的第二原象安全性到192 bit的抗原象性；在0.18 μm ASIC工艺下，QUARK的硬件实现为1 379、1 702、2 296 GE。
文献[9]提出的轻量级杂凑函数族PHOTON，其内部置换函数为类AES^[10]结构。该函数族共有5种参数类型：PHOTON-80/20/16、PHOTON-128/16/16、PHOTON-160/36/36、PHOTON-224/32/32和PHOTON-256/32/32，可提供从64 bit的抗原象安全性到128 bit的抗碰撞性，同时，在0.18 μm ASIC工艺下的最小硬件实现为865 GE。
文献[11]设计了以类PRESENT^[12]算法为内部结构的轻量级杂凑函数族SPONGENT，PRESENT作为轻量级分组密码设计史上的里程碑，其公开后出现了许多基于PRESENT设计的轻量级杂凑函数。其中SPONGENT按输出长度可分为5类:SPONGENT-88/128/160/224/256，共13种参数组合。在安全性方面，最低可保证80 bit的抗原象性、40 bit的抗碰撞性及40 bit的第二原象安全性，最高可提供256 bit的抗原象性、128 bit的抗碰撞性及256 bit的第二原象安全性；在硬件实现方面，在0.13μm ASIC工艺下最小可达到738 GE。另外，SPONGENT-88适用于资源极其受限且对安全性要求低的环境，如用于某些RFID协议和伪随机数产生器；SPONGENT-128/160适用于资源高度受限且对碰撞安全性要求较低的环境；SPONGENT-224和SPONGENT-256分别对应SHA-2和SHA-3的一个子集，这使得SPONGENT能够在普通的轻量级嵌入式环境中兼容标准接口。因此，可以说SPONGENT是目前最有竞争力的轻量级杂凑函数族。
然而，文献[13]提出的统计饱和攻击是一种对缩减轮数的PRESENT很有效的分析方法，SPONGENT内部置换函数采用了类PRESENT结构，因此，统计饱和攻击对SPONGENT有很大威胁。本文针对这一问题，提出一种以海绵结构为整体，内部置换的非线性层采用仿射变换S盒(Affine Transformation S-box，ATS)的轻量级杂凑函数——ATSHash。该函数族包含4个版本的参数组合，提供从40 bit的抗碰撞性至128 bit的第一原象安全性。根据线性、差分性及扩散性选择了原型S盒，仿射变换后的S盒继承了原型S盒优良的密码特性。通过统计饱和分析，仿射变换S盒结构增加了内部置换中线性层特定位扩散路径的复杂度，在很大程度上提高了线性层的混淆性和抗统计饱和攻击能力。
1 ATSHash的安全边界 1.1 海绵结构 海绵结构是一种单向压缩函数，可通过内部迭代结构将任意长度的输入变为固定长度的输出，其整体结构如图 1所示，各参数含义见表 1，其具体压缩步骤可分为以下3步：

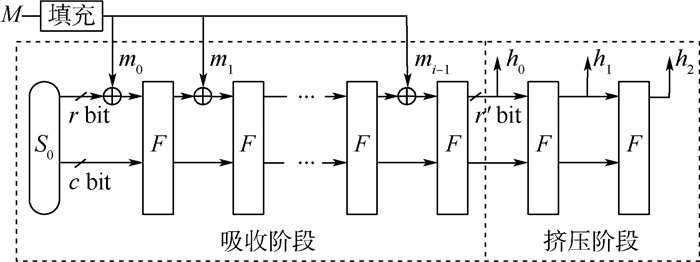图 1 海绵结构框图 Fig. 1 Block diagram of sponge structure

图选项

表 1 海绵结构参数 Table 1 Parameters of sponge structure

参数	含义
M	输入消息
S0	初始迭代状态
mi	第i组分组消息块
hi	输出第i组消息块
r	分组长度
F	内部置换函数
r′	每轮输出消息长度
c	不与消息异或部分长度
b(b=r+c)	内部迭代状态长度
n	输出消息长度

表选项






1) 初始化阶段
将输入消息M先填充一个‘1’，随后补充一定数量的‘0’，使该消息长度为分组长度r的整数倍。例如，消息M为‘001’，分组长度r为8，则填充后的消息M′为‘00110000’，然后，消息按分组长度r进行分组变为{m₀, m₁, …, m_i-1}。
2) 吸收阶段
初始迭代状态S₀与第1组分组消息m₀按位异或，并通过内部置换函数进行迭代，更新迭代后的状态接着与下一组分组消息进行按位异或和迭代过程，重复此步骤，直至最后一组分组消息m_i-1处理完成。
3) 挤压阶段
最后一块分组消息进行内部置换后输出r′ bit，之后再次进行内部置换，每次输出r′ bit直至输出长度达到规定长度n为止。
1.2 安全边界 杂凑函数具有以下安全特性^[14]：①抗碰撞性，即不可能存在多个消息串M₁，M₂，…，M_n对应同一个杂凑值。②第一原象安全性，对一个任意长度的明文消息M，可以很容易得到对应的杂凑值H(M)，而从其信息摘要H(M)很难推出相应的明文消息M。③第二原象安全性：对一个已知的明文消息M₁，很难找到另一个不同的明文消息M₂，使得H(M₁)=H(M₂)。假定在内部置换结构无明显漏洞的情况下，基于海绵结构的杂凑函数，其安全边界中的抗碰撞性为min{2^n/2, 2^c/2}，第一原象安全性为min{2ⁿ, 2^c, max{2^n-r, 2^c/2}}，第二原象安全性为min{2ⁿ, 2^c/2}^[15]。
由于嵌入式系统的资源严格受限，在轻量级应用中的安全性指标不宜过高(如SHA-512)。类似RFID标签的低端嵌入式系统需要64 bit的抗原象安全性，而64 bit或80 bit的原象安全性是目前公认的轻量级应用中的适宜安全指标^[16]。本文根据轻量级杂凑函数结构及同类轻量级杂凑函数的安全下限，提出了4个版本的参数组合，可提供至少72 bit的第一原象安全性、40 bit的第二原象安全性及40 bit的抗碰撞性，如表 2所示。
表 2 同类型轻量级杂凑函数安全边界 Table 2 Security boundaries of similar lightweight hash functions

轻量级杂凑函数	安全性/bit
	第一原象安全性	第二原象安全性	抗碰撞性
ATSHash-88/80/16	72	40	40
ATSHash-88/88/8	80	44	44
ATSHash-144/128/32	112	64	64
ATSHash-144/144/16	128	72	72
SPONGENT-88/80/8	80	40	40
SPONGENT-128/128/8	120	64	64
PHOTON-80/80/16	64	40	40
PHOTON-128/128/16	112	64	64

表选项






表 2中，用输出消息长度n、内部置换中不与消息块异或部分的长度c以及分组长度r来表示不同版本的函数类型，如ATSHash-n/c/r。从表中可以看出，ATSHash的4个版本根据内部置换规模(b=n+r)可分为ATSHash-96和ATSHash-160，对应的输出长度分别为88 bit和144 bit，2种规模的内部置换结构每次分别可吸收每组16 bit、8 bit和32 bit、16 bit的分组消息，可提供从72、40、40 bit至128、72、72 bit的第一原象安全性、第二原象安全性及抗碰撞性，如应用环境需要可根据具体需求调整各个参数。
2 ATSHash的内部置换结构 内部置换结构由非线性层和线性扩散层组成。非线性层由一个原型S盒及4种仿射变换结构生成的仿射等价S盒构成，线性层采用类PRESENT结构，其顶层算法描述如图 2所示。其中，轮数R为b/2，轮常数与内部迭代状态的高16位进行按位异或。

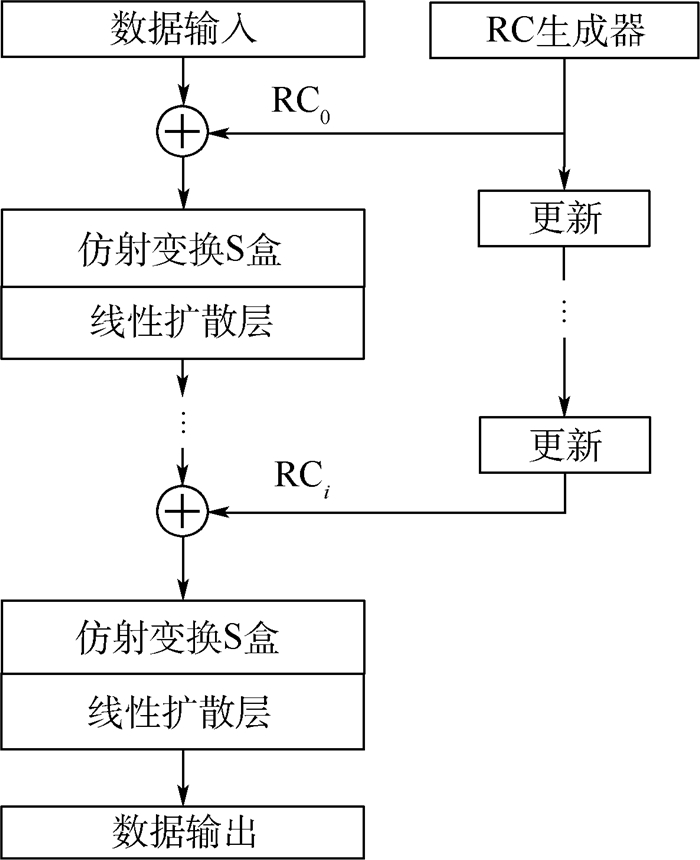图 2 内部置换结构加密流程 Fig. 2 Encryption process of internal permutation structure

图选项

2.1 轮常数 与SPONGENT中采用的14 bit或16 bit的镜像轮常数不同，ATSHash采用截取移位寄存器特定位的方式生成16 bit轮常数，可有效防止滑动攻击。具体来说，轮常数RC_i由一个s bit的线性反馈移位寄存器及其特定位拼接产生，其中s= ，且将寄存器状态定义为x_s-1‖x_s-2‖…‖x₀，每一位寄存器的状态按以下规则每轮进行更新：

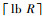
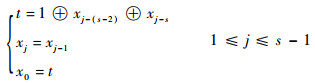(1)

s bit的线性反馈移位寄存器初始状态为全零，c₃‖c₂‖c₁‖c₀为轮常数RC_i状态，且按式(2)对移位寄存器的相应位进行计算：

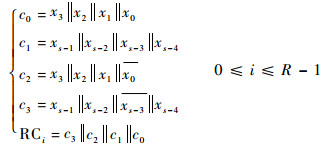(2)

2.2 原型S盒 S盒作为内部置换中的唯一非线性部件，将影响整个结构的安全性。差分均匀度和线性度是反映S盒的抗差分分析及线性分析的重要指标。4 bit S盒的差分均匀度及线性度的下界均不小于4，当2个指标均达到下界时称为最优S盒，该S盒抵抗基本差分分析和线性分析的能力达到最优。Leander和Poschmann^[17]发现在仿射等价的意义下，线性和差分性能最优的S盒有16类，如表 3所示。仿射等价的定义如下：
表 3 最优4 bit S盒的16个仿射等价类^[17] Table 3 Sixteen affine equivalence classes of optimal 4 bit S-box^[17]

S盒	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
G0	0, 1, 2, D, 4, 7, F, 6, 8, B, C, 9, 3, E, A, 5
G1	0, 1, 2, D, 4, 7, F, 6, 8, B, E, 3, 5, 9, A, C
G2	0, 1, 2, D, 4, 7, F, 6, 8, B, E, 3, A, C, 5, 9
G3	0, 1, 2, D, 4, 7, F, 6, 8, C, 5, 3, A, E, B, 9
G4	0, 1, 2, D, 4, 7, F, 6, 8, C, 9, B, A, E, 5, 3
G5	0, 1, 2, D, 4, 7, F, 6, 8, C, B, 9, A, E, 3, 5
G6	0, 1, 2, D, 4, 7, F, 6, 8, C, B, 9, A, E, 5, 3
G7	0, 1, 2, D, 4, 7, F, 6, 8, C, E, B, A, 9, 3, 5
G8	0, 1, 2, D, 4, 7, F, 6, 8, E, 9, 5, A, B, 3, C
G9	0, 1, 2, D, 4, 7, F, 6, 8, E, B, 3, 5, 9, A, C
G10	0, 1, 2, D, 4, 7, F, 6, 8, E, B, 5, A, 9, 3, C
G11	0, 1, 2, D, 4, 7, F, 6, 8, E, B, A, 5, 9, C, 3
G12	0, 1, 2, D, 4, 7, F, 6, 8, E, B, A, 9, 3, C, 5
G13	0, 1, 2, D, 4, 7, F, 6, 8, E, C, 9, 5, B, A, 3
G14	0, 1, 2, D, 4, 7, F, 6, 8, E, C, B, 3, 9, 5, A
G15	0, 1, 2, D, 4, 7, F, 6, 8, E, C, B, 9, 3, A, 5

表选项






若存在F₂上的m阶可逆矩阵A，B和n bit常数a和d，使得2个m×m的S盒S₁和S₂满足：

(3)

则称S₁和S₂是仿射等价的，S盒的差分均匀度和线性度在仿射变换下均保持不变，是S盒的仿射等价不变量。
对于差分均匀度和线性度均达到最优的S盒，如果其具有最大差分概率的差分特征或具有最大偏差的线性特征较多，那么这些特征可被用于多差分密码或多线性密码分析中。具有最大差分概率的差分特征(输入输出差分对)的个数N_D(S)，以及具有最大线性偏差的线性特征(输入输出线性掩码对)的个数N_L(S)的表达式分别为

(4)

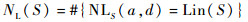(5)

分支数主要用于描述S盒的扩散能力，定义为

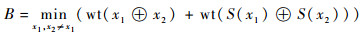(6)

双射S盒分支数不小于2，分支数越大则S盒扩散性越好。
根据式(4)~式(6)计算了16个最优S盒仿射等价类的具有最大差分概率的差分特征的个数、具有最大线性偏差的线性特征的个数及最大分支数，如表 4所示。
表 4 最优4 bit S盒的密码特性 Table 4 Cryptographic properties of optimal 4 bit S-box

S盒	ND(S)	NL(S)	B
G0	24	36	3
G1	24	36	3
G2	24	36	3
G3	15	30	2
G4	15	30	2
G5	15	30	2
G6	15	30	2
G7	15	30	2
G8	24	36	2
G9	18	32	3
G10	18	32	3
G11	15	30	2
G12	15	30	2
G13	15	30	2
G14	18	32	3
G15	18	32	3

表选项






SPONGENT内部置换的S盒与表 3中的G₀仿射等价，PRESENT和RECTANGLE的S盒与G₁线性等价，LBlock的10个S盒皆与G₈仿射等价。通过表 4可以看出，在分支数皆为3的最优S盒中，G₉、G₁₀、G₁₄和G₁₅的N_D(S)和N_L(S)最低。选择G₉作为ATSHash的原型S盒，该S盒与SPONGENT、PRESENT的最大分支数相同，但具有最大差分概率的差分特征个数及具有最大线性偏差的线性特征个数均小于SPONGENT和PRESENT，即在差分分析或线性分析中可被利用的密码特征更少。
2.3 仿射变换S盒 考虑到硬件开销，本文的仿射变换结构均采用线性结构，仿射变换不改变S盒的差分均匀度和非线性度。由式(6)可推得，线性变换亦不改变S盒的分支数。因此，线性仿射变换后的S盒完全继承了原S盒良好的密码特性。从4 bit S盒线性仿射变换的24种结构中任选4种结构，其结构及对应的仿射变换S盒，如表 5所示，其中SS为仿射变换结构的控制逻辑集。
表 5 仿射变换S盒 Table 5 Affine transformation S-boxes

SS	输出	仿射变换S盒
00	y3‖y0‖y2‖y1	S(0)：0, 4, 1, E, 2, 7, F, 3, 8, B, D, 5, 6, C, 9, A
01	y1‖y0‖y3‖y2	S(1)：0, 1, 8, 7, 4, D, F, 9, 2, B, E, C, 5, 6, A, 3
10	y1‖y2‖y3‖y0	S(2)：0, 1, 8, 7, 4, D, F, C, 2, E, B, 9, 5, 3, A, 6
11	y2‖y0‖y3‖y1	S(3)：0, 4, 1, E, 8, D, F, 9, 2, B, 7, 5, C, 6, 3, A

表选项






线性仿射变换结构配置在原型S盒之后，当输入为y₃‖y₂‖y₁‖y₀时，输出如表 5所示，对应生成的仿射变换S盒分别为S⁽⁰⁾、S⁽¹⁾、S⁽²⁾、S⁽³⁾。SS由内部置换的初始迭代状态S₀从高位开始以2 bit分组生成的控制逻辑集决定，即{S_b-1S_b-2, S_b-3S_b-4, …, S_b/2+1S_b/2}，S₀由用户自定义给出(默认值9CA2879031BE56239841F84D)。仿射变换的S盒在海绵结构的第1步消息填充阶段进行配置，一经选定则内部置换中每轮仿射变换的S盒位置不变，仿射变换的S盒有4^b/4种可能组合，相当于加入了b/2 bit的密钥。
2.4 线性扩散层 线性扩散层采用类PRESENT结构，其扩散关系为

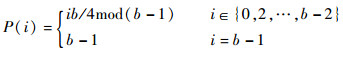(7)

以ATSHash-96为例，其内部置换规模为96 bit的非线性层及线性扩散层结构如图 3所示。

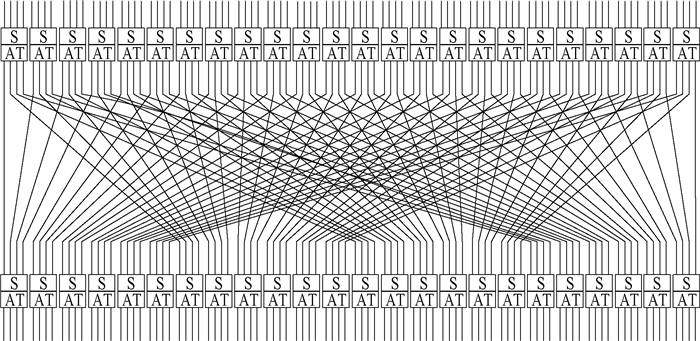图 3 ATSHash-96内部置换结构 Fig. 3 Internal permutation structure of ATSHash-96

图选项

3 安全性分析 在1.2节中已分析过ATSHash外部海绵结构的安全边界，本节主要分析其内部置换结构的安全性，特别是抗统计饱和攻击的安全性。
3.1 差分及线性密码分析 针对差分和线性密码分析，其主要思想是搜索活动S盒个数的方法来评估ATSHash 2种规模的内部置换结构ATSHash-96和ATSHash-160是否存在有效的差分特征和线性逼近。根据2.2节和2.3节中对原型S盒的选取及仿射变换结构可知，仿射变换后的S盒具有良好的差分及非线性特性，其最大差分概率和最大线性逼近优势均为2^-2。表 6为通过计算机搜索2种内部置换结构的活动S盒数量。
表 6 差分活动S盒数量下界 Table 6 Lowest numbers of differentially active S-box

轮数	差分活动S盒数量
	ATSHash-96	ATSHash-160
5	10	10
10	21	24
15	31	41
20	42	56

表选项






20轮的ATSHash-96和ATSHash-160内部置换结构已经不存在有效差分路径和有效线性逼近能将内部置换和随机置换区分开来。因此，b/2轮的ATSHash针对差分和线性密码分析是足够安全的。
3.2 统计饱和攻击 文献[12]提出统计饱和攻击可看做一种特殊的分区分析方法或广义的线性分析方法。其原理是利用分组密码中线性扩散路径的弱点，对于一组给定的明文，通过跟踪每轮固定比特位的扩散路径，分析明文经迭代后的非均匀分布。以PRESENT结构的统计饱和分析为例，寻找含有弱扩散路径的S盒组合。由于每条扩散路径中S盒的数量直接影响了统计饱和分析的难度，数量越多则分析的难度越大、抗统计饱和攻击效果越好。因此，只考虑在最差情况下的统计饱和分析，即一条扩散路径中只有4个S盒的情况。选择线性层结构的弱扩散路径，S盒组合{5, 6, 9, 10}做为分析对象，其扩散路径如图 4所示。

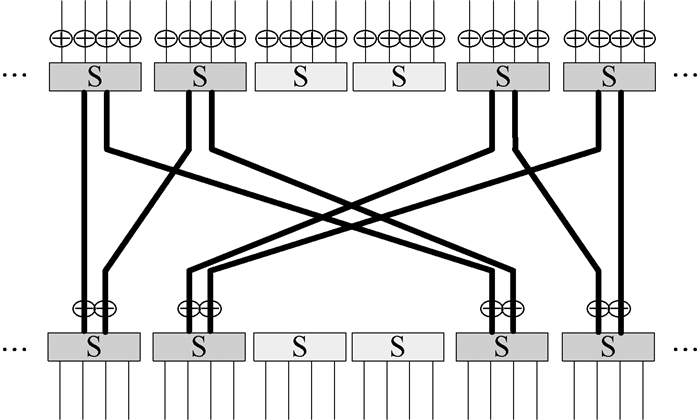图 4 置换层中的弱扩散路径 Fig. 4 Poor diffusion trail in permutation layer

图选项

首先，根据算法1进行正确密钥与猜测密钥加密得出目标8 bit位密文的理论分布。然后，计算特定位正确密钥密文理论分布与猜测密钥密文理论分布之间的距离，根据统计的距离数据，找出距离最短的模型分布，对应的密钥将被接受为正确密钥。
算法1
??输入:子密钥sk输入分布distrib_out[256]。
??输出:输出分布distrib_out[256]。
initial distrib_out[256]to the all-zero state
?for each 8 bit values text do
?for each 8 bit values rand do
??fix the 8 bit trail to text and xor with sk
??fix the 8 bit non trail to rand
??apply the S-box
??apply the permutation
??evaluate the value of the 8-bit trail out
??update distrib_out[out]=distrib_out+distrib_in[text]/256
?end for
end for
为了观察理论分布与实际分布的关系及统计饱和分析的有效性，增加了正确密钥密文理论分布与正确密钥密文实际分布的距离统计。采用固定目标8 bit，其余56 bit随机的方式生成230组明文，并用正确密钥对明文加密，计算正确密钥密文实际分布。图 5给出了经2、4、6、8轮的正确密钥密文实际分布与猜测密钥密文理论分布距离(实际-理论距离，E-T欧氏距离)及正确密钥密文理论分布与猜测密钥密文理论分布距离(理论-理论距离，T-T欧氏距离)统计。其中，已知正确密钥为00100000，通过对E/T-T欧氏距离的观察发现，在密钥32的位置，即00100000，E/T-T欧氏距离都达到最小值。实验表明，统计饱和分析的理论分布模型能够很大程度捕获实际分布的关键分布特征，并利用该分布特征找出正确密钥。

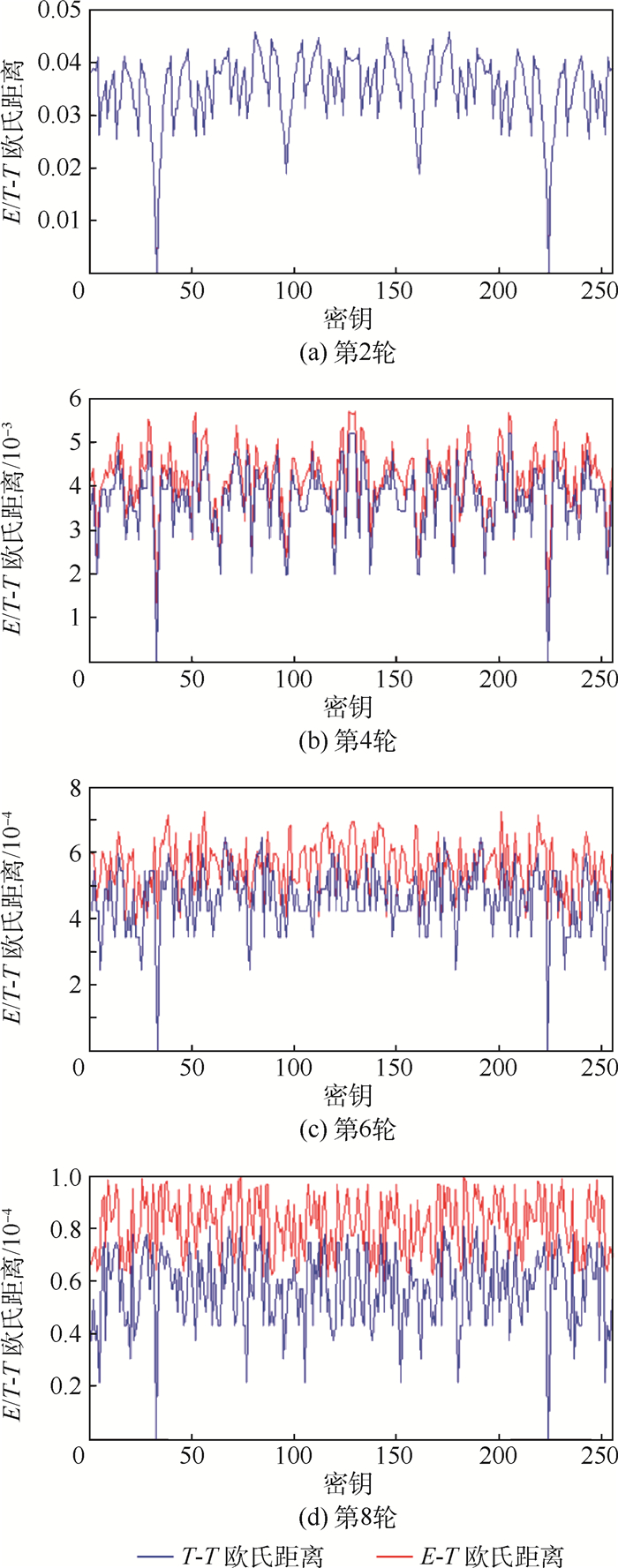图 5 经2、4、6、8轮的E/T-T欧氏距离统计 Fig. 5 E/T-T Euclidean distance statistics after 2, 4, 6 and 8 rounds

图选项

攻击收益^[13]可以很好地评估统计饱和分析在恢复密钥方面的有效性，将其定义为

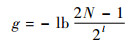(8)

式中：N为候选密钥个数; l为密钥长度。
攻击收益可看成是是衡量计算量的一种尺度，越趋于边界值，统计饱和攻击效果越好(由于明文中固定了8 bit，故其攻击收益边界为8)。为方便比较ATS结构与PRESENT结构抗统计饱和攻击的效果，本节统计饱和分析中的ATS结构采用将PRESENT中S盒替换为仿射变换S盒的方式，其他部分均与PRESENT一致，密钥采用文献[13]中的缩减轮密钥。随机生成4组ATS仿射变换结构排列，分别为031BE56239841F84、AB146D9315CA4982、36218DA26CB92391和AD841-26961112B9C。对2³⁰组固定8 bit的明文经22轮置换后的密文进行分析，ATS结构与PRES-ENT结构的攻击收益对比如图 6所示，其中ATS的仿射变换为ATS-1。

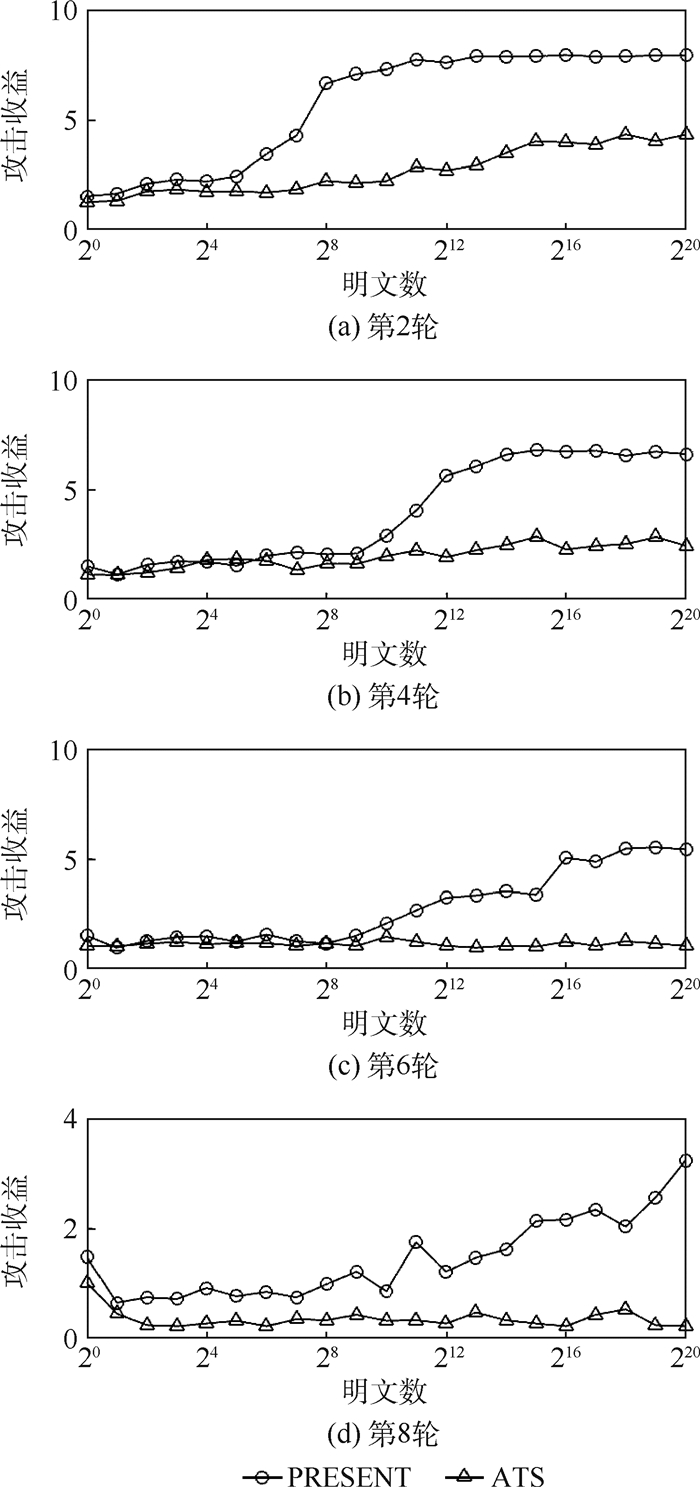图 6 ATS结构与PRESENT结构攻击收益对比 Fig. 6 Gain of attack comparison between ATS and PRESENT construction

图选项

从图 6可以看出，PRESENT结构的攻击收益明显高于ATS结构。在明文数量较少时，两类结构的攻击效果都较差；当固定特定比特位的明文数量增加时，其攻击收益差距逐渐加大。特定轮数下PRESENT结构的攻击收益随明文数量增加而提高，ATS结构的攻击收益除第2轮外并没有明显的随明文数量增加而提高的趋势，且随着解密轮数的增加ATS结构的攻击收益严重衰减。结果表明，ATS结构较PRESENT结构具有更好的抗统计饱和攻击能力。
图 7为4组ATS结构与PRESENT结构均匀/输出分布的平方欧式距离对比。输出分布与均匀分布的距离越小说明输出分布越趋于平均分布，即加密的效果越好，则抗统计饱和攻击的能力越强。从图 7可得，PRESENT结构和ATS结构的均匀/输出分布距离皆随解密轮数的增加而减小，即统计饱和攻击的效果越差。而在特定轮数的ATS结构的均匀/输出分布距离普遍小于PRESENT结构，且随着解密轮数的增加有增大趋势。结果表明，ATS结构的抗统计饱和攻击能力明显优于PRESENT结构。基于仿射变换S盒的ATS结构将弱S盒组合中的特定位重新排列，而ATS结构由用户自定义，相当于又加入了b/2 bit密钥，这使得不能通过简单地追踪特定位的扩散路径进行攻击。因此，ATS结构具有更好的抗统计饱和攻击能力，仿射变换S盒在继承原S盒良好密码特性的基础上，又在很大程度上补偿了PRESENT结构中线性扩散层过于单一、易于对特定位追踪的不足。

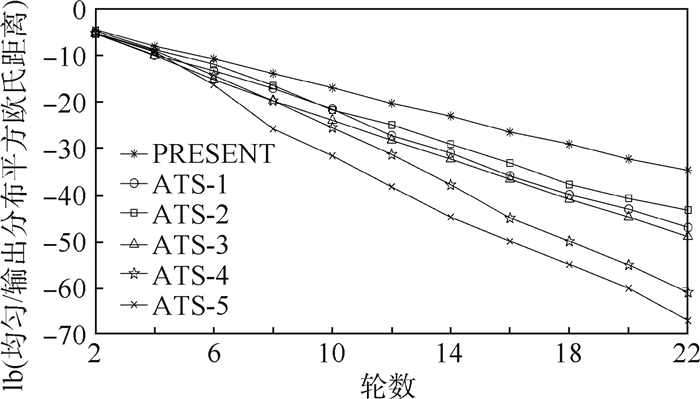图 7 PRESENT结构与ATS结构的均匀/输出分布平方欧氏距离 Fig. 7 Squared Euclidean distance between uniform and output distribution for PRESENT and ATS construction

图选项

4 硬件实现 分别对ATSHash 2种规模的内部置换结构进行了串行和并行硬件实现设计，如图 8和图 9所示。并对ATSHash的2种硬件实现方案进行了功能仿真及逻辑综合，综合环境为DC(Design Compiler)D-2010.03-SP4，其标准器件库为UMCL18G212T3，ATSHash各版本的硬件实现及与同类型轻量级杂凑函数族的对比如表 7所示。

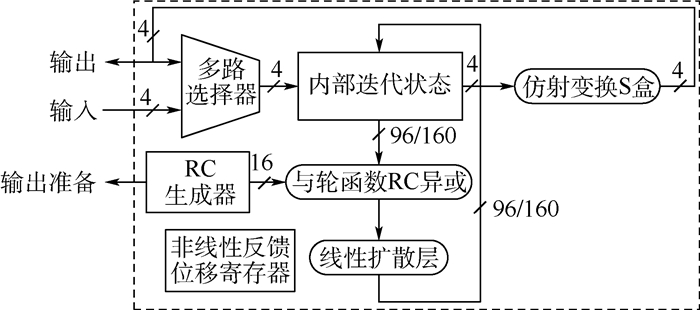图 8 内部置换结构串行硬件实现方案 Fig. 8 Serial hardware implementation scheme of internal permutation structure

图选项

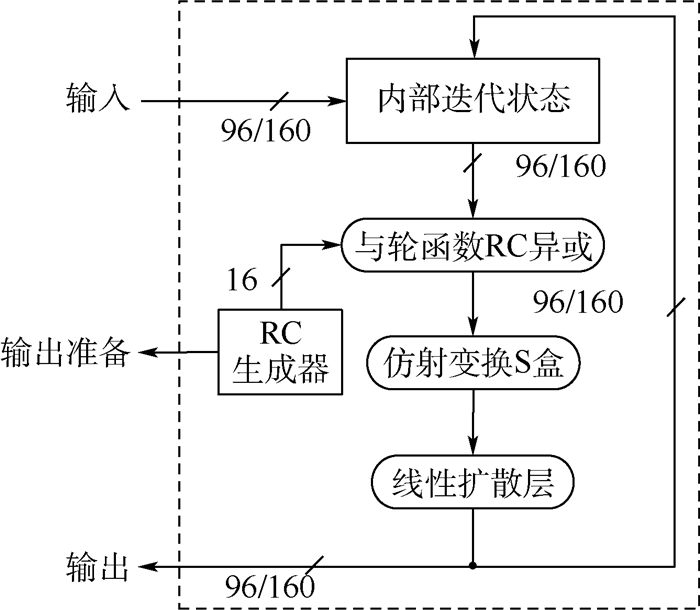图 9 内部置换结构并行硬件实现方案 Fig. 9 Parallel hardware implementation scheme of internal permutation structure

图选项

表 7 同类型轻量级杂凑函数族的硬件实现 Table 7 Hardware implementation of similar lightweight hash functions

轻量级杂凑函数	位宽/ bit	轮数	面积/GE UMC180 nm	吞吐率/(kb·s-1)@100 kHz
ATSHash-88/80/16	4	1 152	832	1.02(0.18 μm)
	96	48	1 334	19.26(0.18 μm)
ATSHash-144/128/32	4	3 200	1 260	0.48(0.18 μm)
	160	80	2 129	16.62(0.18 μm)
SPONGENT-88/80/8	4	990	759	0.81(0.13 μm)
	88	45	1 232	17.78(0.13 μm)
SPONGENT-160/160/16	4	3 960	1 367	0.40(0.13 μm)
	176	90	2 241	17.78(0.13 μm)
PHOTON-80/80/16	4	708	856	2.82(0.18 μm)
	20	132	1 151	15.15(0.18 μm)
PHOTON-128/128/16	4	996	1 394	1.61(0.18 μm)
	24	156	2 172	10.26(0.18 μm)

表选项






ATSHash的内部置换规模分为96 bit和160 bit。串行硬件实现中，非线性层只需要一个ATS盒，每次处理4bit数据，都需要一个5/6bit的非线性反馈移位寄存器(Non-Linear Feedback Shift Register，NLFSR)记录每4 bit分组的位置，处理完内部迭代状态的b bit数据共需要b/4个循环。并行实现时，非线性层需要b/4个S盒，一次循环就可处理完内部置换状态的b bit信息，但其硬件实现开销明显要高于串行实现。因此，用户可根据自己的需求选择合适的硬件实现方法。
仿射变换结构在明文消息处理的填充阶段配置，只需根据用户自定义的初始内部状态S₀和一些简单的逻辑控制单元实现。仿射变换结构在硬件实现中仅是一些简单的连线，在填充阶段配置完成后，并不增加吸收阶段和挤压阶段的硬件开销。
通过表 7可以看出，ATSHash-96在ASIC 0.18 μm工艺下的串/并行实现分别需要832、1 332 GE，内部置换规模160 bit的ATSHash的串/并行实现则分别为1 260、2 129 GE。ATSHash内部结构规模较SPONGENT的规模略大，且增加了仿射变换结构及控制逻辑，故其硬件实现略大于SPONGENT，但其安全边界也因内部规模的增加而提高。除ATSHash-96与SPONGENT-88的并行实现外，在类似的内部置换规模下ATSHash与SPONGENT的硬件开销均低于PHOTON。
5 结论 本文针对SPONGENT中的PRESENT结构线性层过于简单，易受统计饱和分析方法攻击的问题，提出了一种基于仿射变换S盒的轻量级杂凑函数，计算了16种最优4 bit S盒仿射等价类的差分均匀度、线性偏差及扩散特征指标，分析对比了仿射变换S盒结构与PRESENT结构的抗统计饱和攻击能力，设计并实现了ATSHash的串/并行硬件实现，得出如下结论：
1) 在最大分支数一样的情况下，具有最大差分概率的差分特征个数及具有最大线性偏差的线性特征个数越小，在差分分析或线性分析中可被利用的密码特征越少，且线性仿射变换结构不改变原S盒的密码特性。
2) 基于仿射变换S盒的结构改变了线性层的扩散方式，使得不可能通过追踪上一轮S盒输出的固定比特位进行攻击，在相同线性层结构的条件下，非线性层中仿射变换结构的加入增加了统计饱和攻击的复杂度，在很大程度上弥补了PRESENT中线性层结构单一的不足。
3) 基于海绵结构的轻量级杂凑函数的安全边界及硬件实现主要取决于内部置换结构，ATSHash的规模略大于SPONGENT，且增加了仿射变换的控制逻辑，因此其硬件实现略大于SPONGENT，但同时ATSHash抗统计饱和攻击能力较SPONGENT更高。

参考文献

[1]	MURAMATSU J, MIYAKE S. Hash property and fixed-rate universal coding theorems[J].IEEE Information Theory Society, 2010, 56(6): 2688–2698.DOI:10.1109/TIT.2010.2046214
[2]	SAM L, SAM A, PATRICK V T, et al. Wearable flexible lightweight modular RFID tag with intergrated energy harvester[J].IEEE Transactions on Microwave Theory and Techniques, 2016, 64(7): 2304–2314.DOI:10.1109/TMTT.2016.2573274
[3]	IGNACIO A B, CLAUDIA F U, RENE C, et al. Design and implementation of a non-pipelined MD5 hardware architecture using a new functional description[J].IEICE Transactions on Information and Systems, 2008, E91-D(10): 2519–2523.DOI:10.1093/ietisy/e91-d.10.2519
[4]	HILARIE O. Recent parables in cryptography[J].IEEE Internet Computing, 2014, 18(1): 82–86.DOI:10.1109/MIC.2014.13
[5]	WILLIAM E B. A new hash competition[J].IEEE Security & Privacy, 2008, 6(3): 60–62.
[6]	AUMASSON J P, HENZEN L, MEIER W, et al. Quark:A lightweight hash[J].Journal of Cryptology, 2013, 26(2): 313–339.DOI:10.1007/s00145-012-9125-6
[7]	DING L, JIN C H, GUAN J. New state recovery attacks on the Grain v1 stream cipher[J].China Communication, 2016, 13(11): 180–188.DOI:10.1109/CC.2016.7781728
[8]	CANNIōRE D, DUNKELMAN O, KNE?EVIC'M. KATAN and KTANTAN: A family of small and efficient hardware-oriented block ciphers[C]//Proceedings of 11th International Workshop on Cryptographic Hardware and Embedded Systems. Berlin: Springer, 2009: 272-288.
[9]	GUO J, PEYRIN T, POSCHMANN A, et al. The PHOTON family of lightweight hash functions[C]//Advances in Cryptology-CRYPTO. Berlin: Springer, 2011: 222-239.
[10]	ISSAM H, KAMAL E S, EZZ E M, et al. High-speed AES encryptor with efficient merging techniques[J].IEEE Embedded Systems Letters, 2010, 2(3): 67–71.DOI:10.1109/LES.2010.2052401
[11]	BOGDANOV A, KNEZENIV M, LEANDER G. SPONGENT:The design space of lightweight cryptographic hashing[J].IEEE Transactions on Computers, 2013, 62(10): 2041–2053.DOI:10.1109/TC.2012.196
[12]	BOGDANOV A, KNEZENIV M, LEANDER G. PRESENT: An ultra lightweight block cipher[C]//Proceedings of 9th International Workshop on Cryptographic Hardware and Embedded Systems. Berlin: Springer, 2007: 450-466.
[13]	COLLARD B, STANDAERT F X. A statistical saturation attack against the block cipher PRESENT[C]//The Cryptographers Track at RSA Conference 2009. Berilin: Springer, 2009: 195-211.
[14]	CHARANJIT S J, ANINDYA C P. Provably good codes for Hash function design[J].IEEE Transactions on Information Theory, 2009, 55(1): 33–45.
[15]	BERTONI G, DAEMEN J, PEETERS M. Sponge based pseudo-random number generators[C]//Proceedings of 12th International Conference Cryptographic Hardware and Embedded Systems. Berlin: Springer, 2010: 33-47.
[16]	LIM C, KORKISHKO T. MCrypton: A lightweight block cipher for security of low-cost RFID tags and sensors[C]//Information Security Applications: 6th International Workshop, WISA 2005. Berlin: Springer, 3786: 243-258.
[17]	LEANDER G, POSCHMANN A. On the classification of 4 bit S-BOX[C]//Arithmetic of Finite Fields: First International Workshop, WAIFI 2007. Berlin: Springer, 2007: 159-176.