晶界(GB)本身就相当于一个非常复杂的缺陷,高温变形条件下,结构的失效往往从晶界处发生。由于晶界结构与晶粒内不同,存在多种缺陷及应力场,一些杂质元素倾向于在晶界处偏聚和扩散,形成置换原子或者溶解间隙原子。这些点缺陷参与扩散过程,能够充当质量传递的介质,极具研究意义。例如,晶界氧化[3-4]和氢元素引起的脆化[5]将分别导致晶间应力腐蚀开裂和合金的脆性断裂。中国开发出的低偏析高温合金系列,降低了S、P和Si等杂质的含量,使承温能力比原型合金提高20~25℃,采用Mg偏聚晶界的微合金化技术,显著提高了合金的强度和塑性[1]。
已有大量的理论实验研究关于合金化元素在Ni中的偏析[4, 6-8]和元素对Ni的作用[9-11],表明化学成分是影响晶界性质并决定材料性能的最重要的因素,元素在晶界上的偏析是改变化学成分的普遍途径。精确控制合金成分,有效去除杂质,或者将含量控制在较低水平,是提升高温合金性能的关键环节,对于旨在优化晶界性能的晶界工程有着重要意义。俄歇谱仪分析显示,微量元素偏聚在晶界上会脆化金属[12]。Bagot等[13]通过原子力探针扫描(atom probe tomography)技术研究Ni基合金RR1000,在晶界上发现了Cr、Mo和B等元素,并且检测到了C元素的富集,尽管不如B元素的含量显著。理论研究方面,Razumovskiy等[14]使用Rice-Thomson-Wang模型研究了4d和5d过渡族金属元素对典型的大角度Ni晶界结合力的影响,然后在粉末冶金的Ni合金中加入理论研究筛选出的元素Zr、Hf、Nb、Ta和B,计算结果与实验符合得很好,通过调整化学成分提升了合金的力学性能。V?ianská和?ob[15]发现偏析的sp轨道杂化元素极大降低了Ni原子的磁性,Ga、Te、Sb、In和Sn等元素使Ni脆化。对于轻质元素H,Stefano等[16]发现它容易被晶界吸引,以晶界为通道快速扩散,在晶界上的偏析则不显著。
目前,理论研究主要集中在单个元素的偏析行为及对合金的强化/脆化作用,关注共偏析影响和多种元素相互作用的研究还非常少。对于偏析元素相互作用的研究,可以为合金设计者提供有价值的信息,保护合金不被有害元素侵袭,提高合金纯洁度,保持有益元素持续发挥作用,改善合金性能,延长使用寿命。另外,利用第一性原理计算方法,实现了研究单一杂质、避免其他成分干扰的构想,弥补了实验方法的短板,从而揭示原子尺度上的作用机制,为多种元素共同作用的研究打下基础[17]。
本文着眼于元素之间的相互作用,采用基于密度泛函理论的第一性原理计算方法,选取2种典型的Ni晶界结构,研究了14种常用过渡族合金化金属元素和C、H、O、N和B 5种非金属元素在Ni晶界上的偏析规律。
1 计算方法 本文采用维也纳大学开发的软件包VASP(Vienna Ab initio Simulation Package)[18]完成计算。利用GGA-PW91广义梯度近似泛函[19]来描述交换关联能,使用PAW势[20]处理电子与核的相互作用,Ni最外层16个电子均作为价电子处理。平面波截断能为400 eV。在倒易空间中使用Monkhorst-Pack方法确定k点。Σ3晶界超胞的k点网格为3×3×1,Σ5晶界超胞的k点网格为2×2×1。所有Ni相关的计算都设置了自旋极化。能量收敛判据为2个电子步之间总能变化小于10-5 eV,原子间作用力小于0.03 eV/(10-10 nm)。
基于重合位置点阵(CSL),本文选取2个典型[15, 21-22]的Ni晶界结构,密排的晶界和含有较多孔隙的晶界(以下分别简写为Σ3和Σ5晶界)进行研究。采用Java应用Grain Boundary Studio[23]构建晶界初始原子结构,依据计算出的体材料的晶格常数,生成3D周期性模型,用于后续第一性原理计算。
结构优化中所有原子都得到了松弛。为了忽略周期性结构中2个相邻晶界之间的相互作用引起的计算误差,同时控制因体系结构增大而附加的计算量,需要确定合适的超胞大小。最终选取的Σ3晶界包含12层原子,晶格常数为a=7.42×10-10 nm, b=7.42×10-10 nm, c=24.23×10-10 nm,共108个原子。Σ5晶界包含20层原子,晶格常数为a=7.00×10-10 nm, b=7.82×10-10 nm, c=15.64×10-10 nm,共80个原子。晶界的能量跟文献[16]作了对比,证明超胞大小是合适的。
为了描述晶界结构的稳定性,定义晶界能γGB的计算公式为
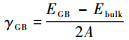 | (1) |
式中:EGB为晶界超胞的总能;Ebulk为相同原子数块体Ni的总能;A为充分弛豫后的界面面积。取因数2表示一个超胞中包含了2个晶界。γGB越小,晶粒的结合强度越高。
定义溶解能Esol来描述元素溶于合金的能力, 其计算公式为
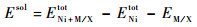 | (2) |
式中:ENi+M/Xtot为含有金属添加元素M或非金属添加元素X的晶界超胞总能;ENitot为只含有Ni的超胞总能;EM/X为单个M/X原子在块体材料中的能量。
合金化原子M和非金属原子X之间相互作用能ΔEMX的计算公式[24]为
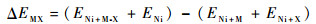 | (3) |
式中:ENi+M-X为包含M-X原子对的Ni超胞总能;ENi为纯Ni超胞的总能;ENi+M和ENi+X分别为包含一个金属M原子和一个非金属X原子的超胞总能。当ΔEMX为负值,M和X之间互相吸引;当ΔEMX为正值,M和X之间互相排斥。也就是说,金属M原子对轻质元素X的偏析有促进或者抑制作用。
2 结果与讨论 2.1 晶界结构 构建的2个Ni晶界结构沿[001]方向的视图如图 1所示。虚线表示晶界平面,数字由小到大依次标出离界面(0层)由近到远,一直到块体区域的原子层编号。
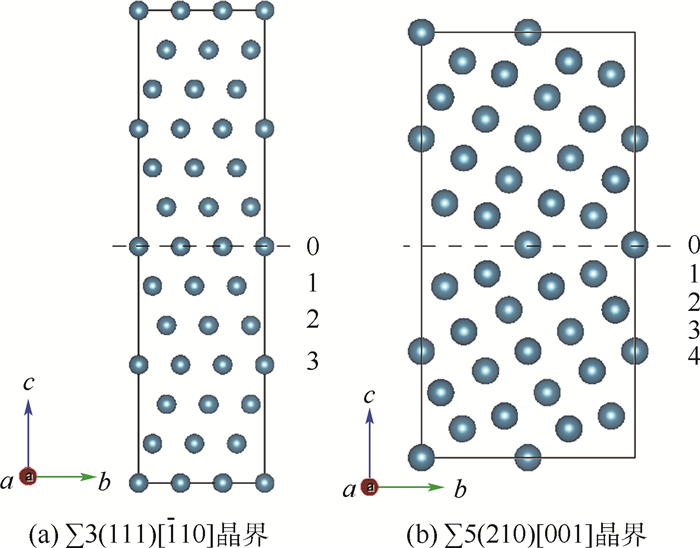 |
| 图 1 2种晶界弛豫后沿[001]方向结构 Fig. 1 Two relaxed grain boundary structures viewed along [001] direction |
| 图选项 |
从图 1可以看出,Σ3晶界平面上原子排布较密,Σ5晶界上原子排布疏松,含有较大孔洞。由晶界面上原子数N与晶界面积A的比值,
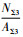
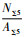
2.2 合金化金属元素的偏析行为 晶界上的易偏析元素会对合金的结构与性能产生不同的影响[5, 8-9]。有益微量元素是冶炼过程中有意加入的,如稀土元素以及Mg、Ca、Ba、Zr和Hf等,它们改善原子间的键合状态,加强界面结合力,提升合金的高温强度,同时抑制含有害元素的低熔点化合物或共晶产物在晶界生成,阻碍有害杂质向晶界偏析。有害元素来自炼钢的原材料和冶炼过程中的环境及设备污染,可降低晶界结合力[2]。
Ni合金中常用的合金化元素有Cr、Co、Mo、Al、Fe、Ti、Mn、Cu、Ta、Zr、Hf、W、Re和Ru等,均包含在本文研究范围内。其中,Cr、W、Mo、Ta、Re和Ru都是有效的固溶强化元素[2]。由于合金化元素原子半径较大,不易占据间隙位置,通常替代Ni原子。
各类合金化元素在Σ3和Σ5晶界不同位置处的溶解能计算结果如图 2(a)和图 2(b)所示。总的来说,在距离晶界较远的地方,即近似块体的区域,溶解能趋于平衡。2种晶界的溶解能曲线各不相同。Σ3晶界的曲线趋于水平,表明合金化元素没有明显的偏析倾向,在体材料区域较稳定。而Σ5晶界的能量曲线波动比较明显,大多数元素倾向于向晶界偏析,并呈现出2种不同的趋势,原子尺寸是主要的影响因素[1, 8]:比Ni尺寸更大的原子,如Ta、Al、Zr、Hf和Ti,在晶界的次近邻原子层上有最稳定的取代位置;尺寸略小的原子,如Cr、Co和Re等,在晶界平面的最近邻原子层有最稳定的位置。
 |
| 图 2 溶解能随合金化元素占晶界不同原子层的变化 Fig. 2 Variation of solution energy with alloying elements doped at different layers |
| 图选项 |
2.3 非金属元素的偏析行为 高温合金对杂质含量的控制有严格要求。气体元素H、O和N严重损害高温合金的力学性能。C元素能强化晶界,应用于几乎所有的高温合金中。B元素能够增大界面原子间结合力,减少晶界缺陷,析出少量颗粒相[1-2]。
B元素的溶解度大于C元素,小于替代式合金化元素,往往认为它在晶界空位处偏析,属于非平衡偏析性质。本文通过计算验证了这一点。B元素在间隙位置的溶解能是-0.89 eV,低于其在替代位置的能量5.16 eV。
对于H、O和N元素,选用单个分子计算能量,对于B和C元素,则在晶体结构数据库ICSD中寻找常温下稳定的晶体构型计算能量。对于基态是顺磁的H2和O2分子,在计算中开启自旋极化。非金属元素单个原子能量计算的截断能均取400 eV,与晶界计算的截断能保持一致。各项计算中k点的数量均经过校正,确保能代表性地描述各类结构。得到的H、C、O、N和B单个原子的能量分别为-1.12、-9.10、-4.90、-8.33和-6.69 eV。
选取间隙原子位置时,首先在晶界平面的孔洞上取若干个点,其中Σ5晶界选取的位置如图 3所示。至于Σ3晶界,由于周期性和对称性,平面上的孔洞位置取一个即可,不于图中再作表述。
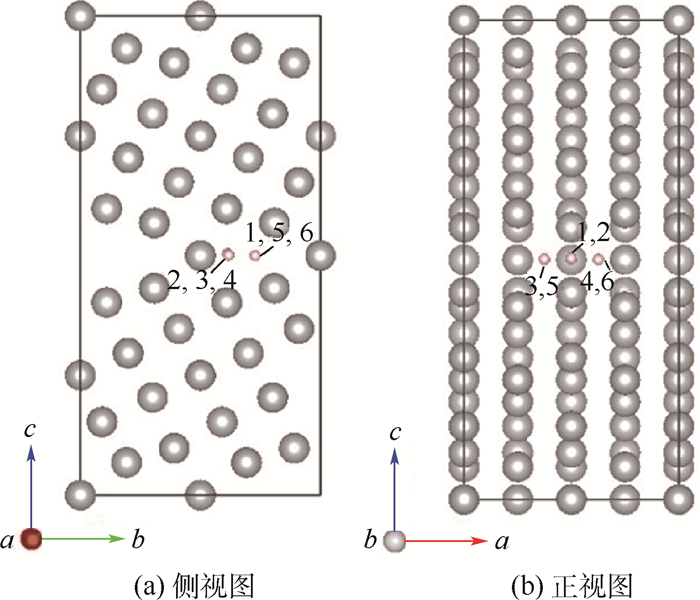 |
| 图 3 Σ5晶界平面上间隙位置 Fig. 3 Doping sites at Σ5 GB interface plane |
| 图选项 |
对应于图 3,非金属杂质Σ5晶界孔洞处的溶解能Esol(下标为各元素)计算结果如表 1所示。可以看出,在对称位置5和6,各个非金属原子都达到了最低能量,即为孔洞处的最稳定位置。
表 1 单个非金属原子占据Σ5晶界孔洞处不同位置的溶解能 Table 1 Solution energy of Σ5 grain boundary containing one nonmetallic atom at different sites on hollow of GB planeeV
| eV | |||||
| Σ5晶界间隙位置 | EHsol | ECsol | EOsol | ENsol | EBsol |
| 1 | -1.693 | 0.747 | -1.165 | -1.146 | -0.899 |
| 2 | -1.691 | 0.583 | -0.880 | -1.683 | -0.898 |
| 3 | -1.736 | 0.745 | -1.539 | -1.459 | -0.899 |
| 4 | -1.736 | 0.744 | -0.968 | -1.459 | -0.899 |
| 5 | -1.736 | 0.744 | -1.541 | -1.461 | -0.900 |
| 6 | -1.736 | 0.743 | -1.541 | -1.462 | -0.900 |
表选项
根据得到的非金属杂质位于晶界附近一直到块体区域的四面体和八面体间隙的能量,研究元素在结构中的整体偏析倾向。表 2列出了间隙原子在晶界上和远离晶界的块体区域溶解能之差,o代表八面体间隙,t代表四面体间隙。差值为负则表示元素倾向于偏析在晶界上。与金属元素在晶界中的偏析趋势相似,所有非金属元素都倾向于偏聚在Σ5晶界上,而Σ3晶界吸引到的元素寥寥无几。在Σ3晶界中能发现的规律是,元素更倾向于块体区域中八面体间隙的位置。回到偏析现象明显的Σ5晶界,C和B表现出了相似的偏析行为,它们都驻留在靠近界面的位置。这一现象与实验中的发现相吻合[13, 25]。
表 2 间隙原子在晶界和块体处的溶解能差值 Table 2 Solution energy differences of interstitial atoms at grain boundary and bulkeV
| eV | ||||||
| 晶界 | 间隙 | H | C | O | N | B |
| ∑3 | o | 0.280 | 0.038 | 0.562 | 1.235 | -0.012 |
| t | 0.008 | 0.067 | 0.078 | 0.073 | 0.070 | |
| ∑5 | o | -0.281 | -1.519 | -2.111 | -0.650 | -1.857 |
| t | -0.196 | -0.474 | -0.314 | 0.154 | -0.394 | |
表选项
2.4 元素在Ni晶界上的共偏析作用 加入多种微量元素,意在通过元素之间的协同作用获得更好的强韧化效果[11]。由于∑5晶界上元素的偏析行为比∑3晶界上明显得多,本节仅对∑5晶界进行元素相互作用的研究。选取有明显偏析倾向的金属元素Ru、Re、W、Zr、Hf和Ta,以及2.3节的5种非金属元素,将其分别置于各自最稳定的位置,如图 4所示,数字1~5代表晶界附近金属原子可能占据的原子层,由图 2可知3号为稳定位置,非金属原子在6号位置,计算相互作用能。
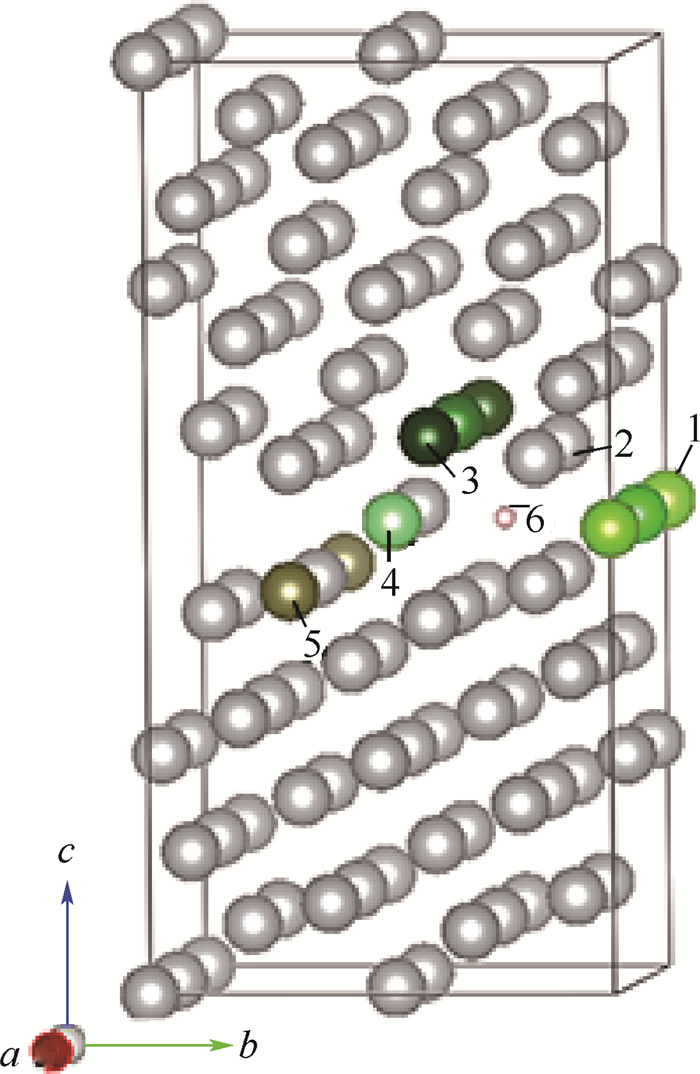 |
| 图 4 金属与非金属元素在晶界上各自最稳定的位置 Fig. 4 The most stable positions of metallic and nonmetallic elements on grain boundaries |
| 图选项 |
相互作用能的计算结果如图 5所示。由图中可知,金属元素对C和H的作用有相似之处:略微吸引C,较强地排斥H。这意味着所有元素都可以促进C在晶界的偏析,而抑制H的偏析。对于O和N来说,Ru、Re、W、Ta与O的相互作用能绝对值大,且为正值,体现出强烈的排斥作用,推知Ru、Re、W和Ta可以提升晶界的抗氧化性。然而它们对N的排斥作用比较弱。对于常用的晶界强化元素B,Ru、Re和W能够产生吸引作用,而Zr、Hf和Ta对其是排斥作用。Ta对H的排斥作用强,可在晶界抗氢脆方面发挥有益作用。
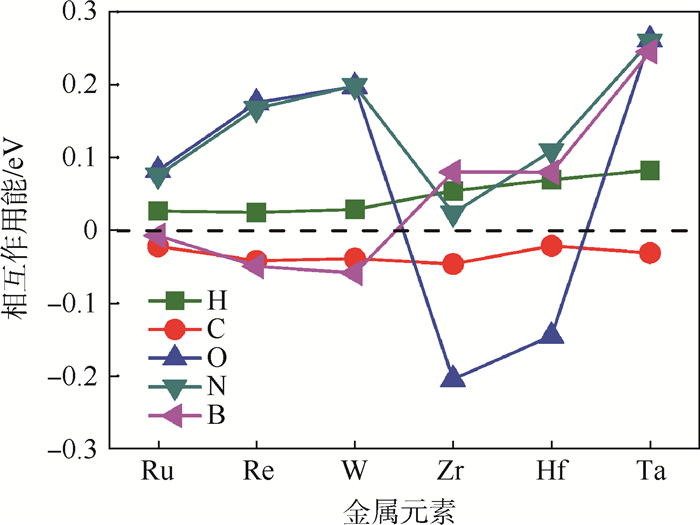 |
| 图 5 强偏析金属元素与非金属元素在∑5晶界上的相互作用能 Fig. 5 Interaction energies between metallic elements with significant segregation tendency and nonmetallic elements on ∑5 grain boundary |
| 图选项 |
3 结论 1) 通过第一性原理计算研究了金属元素(14种过渡族合金化元素)和非金属元素(C、H、O、N和B)在晶界上的的偏析行为,以及它们的相互作用。在本文所研究的元素当中,密排结构、晶界能低的∑3晶界没有体现出明显偏析现象。对于含有较多孔隙、晶界能较高的∑5晶界,可以总结出以下偏析规律:Cu、Mn和Ru倾向于占据在晶界平面,而Ta、Al、Zr、Hf和Ti在晶界的第二近邻原子层有更稳定的位置,Cr、Co和Re的最稳定位置在晶界的第一近邻原子层。非金属元素倾向于占据在晶界上的孔洞位置。
2) 合金化元素与非金属杂质的相互作用研究结果表明,Zr和Hf显示出对O强烈的吸引作用,Ta对O、N和B有强烈的排斥作用。以计算结果为基础,可以推想,Ru、Re、W和Ta能够抑制晶界的氧化作用,Ta可以有效地阻止氢脆效应,是良好的抑制杂质偏析的元素。以上结论可以为Ni合金的晶界工程提供参考。
参考文献
| [1] | 黄乾尧, 李汉康. 高温合金[M].北京: 冶金工业出版社, 2000: 3. HUANG Q Y, LI H K. Superalloys[M].Beijing: Metallurgical Industry Press, 2000: 3.(in Chinese) |
| [2] | 郭建亭. 高温合金材料学[M].北京: 科学出版社, 2008: 4. GUO J T. Materials science and engineering for superalloys[M].Beijing: Science Press, 2008: 4.(in Chinese) |
| [3] | VISKARI L H, RNQVIST M, MOORE K L, et al. Intergranularcrack tip oxidation in a Ni-base superalloy[J].Acta Materialia, 2013, 61(10): 3630–3639.DOI:10.1016/j.actamat.2013.02.050 |
| [4] | ALEXANDROV V, SUSHKO M L, SCHREIBER D K, et al. Ab initio modeling of bulk and intragranular diffusion in Ni alloys[J].Journal of Physical Chemistry Letters, 2015, 6(9): 1618–1623.DOI:10.1021/acs.jpclett.5b00177 |
| [5] | BECHTLE S, KUMAR M, SOMERDAY B P, et al. Grain-boun-dary engineering markedly reduces susceptibility to intergra-nular hydrogen embrittlement in metallic materials[J].Acta Materialia, 2009, 57(14): 4148–4157.DOI:10.1016/j.actamat.2009.05.012 |
| [6] | ANGELO J E, MOODY N R, BASKES M I. Trapping of hydrogen to lattice defects in nickel[J].Modelling & Simulation in Materials Science & Engineering, 1995, 3(3): 289–307. |
| [7] | DINGREVILLE R, BERBENNI S. On the interaction of solutes with grain boundaries[J].Acta Materialia, 2016, 104: 237–49.DOI:10.1016/j.actamat.2015.11.017 |
| [8] | 刘文冠. 基于第一性原理的镍基合金晶界脆化机理的理论研究[D]: 北京: 中国科学院大学, 2014: 37. LIU W G. First-principles study of intergranular embrittlement in Ni-based alloy[D]: Beijing: University of Chinese Academy of Sciences, 2014: 37(in Chinese). |
| [9] | SINGH N, TALAPATRA A, JUNKAEW A, et al. Effect of ternary additions to structural properties of NiTi alloys[J].Computational Materials Science, 2016, 112: 347–355.DOI:10.1016/j.commatsci.2015.10.029 |
| [10] | AI C, LI S, LIANG Y, et al. Influence of Mo and Ta additions on solidification behavior of Ni3Al single crystal alloys[J].Progress in Natural Science:Materials International, 2015, 25(4): 353–360.DOI:10.1016/j.pnsc.2015.07.001 |
| [11] | ZHAO W, SUN Z, GONG S. Synergistic effect of co-alloying elements on site preferences and elastic properties of Ni3Al:A first-principles study[J].Intermetallics, 2015, 65: 75–80.DOI:10.1016/j.intermet.2015.06.006 |
| [12] | 周自强. 晶界研究的现状和发展[J].北京航空航天大学学报, 1989, 3(3): 117–124. ZHOU Z Q. Recent progress and development on grain boundary research[J].Journal of Beijing University of Aeronautics and Astronautics, 1989, 3(3): 117–124.(in Chinese) |
| [13] | BAGOT P A J, SILK O B W, DOUGLAS J O, et al. An atom probe tomography study of site preference and partitioning in a nickel-based superalloy[J].Acta Materialia, 2017, 125: 156–165.DOI:10.1016/j.actamat.2016.11.053 |
| [14] | RAZUMOVSKIY V I, LOZOVOI A Y, RAZUMOVSKⅡ I M. First-principles-aided design of a new Ni-base superalloy:Influence of transition metal alloying elements on grain boundary and bulk cohesion[J].Acta Materialia, 2015, 82: 369–377.DOI:10.1016/j.actamat.2014.08.047 |
| [15] | V?IANSKá M, ?OB M. The effect of segregated sp-impurities on grain-boundary and surface structure, magnetism and emb-rittlement in nickel[J].Progress in Materials Science, 2011, 56(6): 817–840.DOI:10.1016/j.pmatsci.2011.01.008 |
| [16] | STEFANO D D, MROVEC M, ELS?SSER C. First-principles investigation of hydrogen trapping and diffusion at grain boundaries in nickel[J].Acta Materialia, 2015, 98: 306–312.DOI:10.1016/j.actamat.2015.07.031 |
| [17] | ZHANG S, KONTSEVOI O Y, FREEMAN A J, et al. First pric-iples investigation of zinc-induced embrittlement in an alumi-num grain boundary[J].Acta Materialia, 2011, 59(15): 6155–6167.DOI:10.1016/j.actamat.2011.06.028 |
| [18] | KRESSE G, FURTHMVLLER J. Efficiency of Ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set[J].Computational Materials Science, 1996, 6(1): 15–50.DOI:10.1016/0927-0256(96)00008-0 |
| [19] | ERNZERHOF M. Generalized gradient approximation made simple[J].Physical Review Letters, 1996, 77(18): 3865.DOI:10.1103/PhysRevLett.77.3865 |
| [20] | PERDEW J P, CHEVARY J, VOSKO S, et al. Atoms, molecules, solids, and surfaces:Applications of the generalized gradient approximation for exchange and correlation[J].Physical Review B, 1992, 46(11): 6671.DOI:10.1103/PhysRevB.46.6671 |
| [21] | LIU W, HAN H, REN C, et al. Effects of rare-earth on the coh-esion of Ni ∑5(012) grain boundary from first-principles ca-lculations[J].Computational Materials Science, 2015, 96: 374–378.DOI:10.1016/j.commatsci.2014.09.035 |
| [22] | XIA S, ZHOU B X, CHEN W J, et al. Effects of strain and annealing processes on the distribution of ∑3 boundaries in a Ni-based superalloy[J].Scripta Materialia, 2006, 54(12): 2019–2022.DOI:10.1016/j.scriptamat.2006.03.014 |
| [23] | OGAWA H. GBstudio:A builder software on periodic models of CSL boundaries for molecular simulation[J].Materials Transactions, 2006, 47(11): 2706–2710.DOI:10.2320/matertrans.47.2706 |
| [24] | 祝令刚. Ti和Nb合金中氧化问题的理论研究[D]. 沈阳: 中国科学院金属研究所, 2013: 84. ZHU L G. Theoretical study on the oxidation of Ti and Nb-based alloys[D]. Shenyang: Insititute of Metal Research, Chinese Academy of Sciences, 2013: 84(in Chinese). |
| [25] | ALAM T, FELFER P J, CHATURVEDI M, et al. Segregation of B, P, and C in the Ni-based superalloy, inconel 718[J].Metallurgical and Materials Transactions A, 2012, 43(7): 2183–2191.DOI:10.1007/s11661-012-1085-9 |
