国内外已进行多次深空探测活动,且多采用腿式缓冲机构实现软着陆[2]。针对探测器的软着陆稳定性,各国****进行了大量的研究工作。文献[3-5]提出了探测器软着陆过程的动力学仿真分析方法,并给出了影响探测器着陆稳定性的关键因素。文献[6-8]在未考虑主发动机推力影响的情况下,采用蒙特卡罗模拟分析了非零高度关机着陆方案下不同着陆工况对探测器着陆缓冲性能及稳定性能的影响。文献[9-11]在对非零高度关机着陆方案下着陆性能的研究中引入了主发动机推力模型,但未考虑发动机推力受控变化过程。文献[12-13]则指出软着陆过程中主发动机作用时间增长对探测器软着陆稳定性具有消极影响。
为了改善腿式探测器高度关机方案失效时主发动机长时间作用对软着陆稳定性的影响,提出触地关机方案。触地关机方案指在探测器与星球表面接触后实施关闭主发动机操作,以尽可能减小主发动机推力作用的消极影响;本文进一步考虑在这一过程中引入实时姿态控制(姿控),提高探测器软着陆稳定性。针对触地关机方案,建立了新型探测器的ADAMS动力学分析模型,并引入变推力主发动机及姿控推进器的推力控制模型。而后采用蒙特卡罗模拟对多种着陆方式下探测器的着陆稳定性进行对比分析,为触地关机方案的设计提供参考。
1 探测器构型及动力学建模 1.1 探测器构型及坐标系定义 探测器整体构型如图 1所示,可分为主体及4个相对独立的着陆缓冲机构。主体为各种探测仪表及控制分系统的安装平台,每套着陆缓冲机构由3个以倒三角形式布置的缓冲支柱(主支柱、辅助支柱)及一个固连于主支柱末端的足垫组成。辅助支柱通过万向节与主体连接,主支柱与固连在主体上的缓冲杆通过万向节连接。缓冲杆主要是为了限制通过主支柱传递给主体的冲击力,从而起到保护探测器有效负载的作用。
 |
| 图 1 探测器构型 Fig. 1 Structures of explorer |
| 图选项 |
本文采用ADAMS进行动力学建模。坐标系定义如图 2所示,其中,OS-XSYSZS为空间全局坐标系;OC-XCYCZC为质心控制坐标系;αe为着陆面等效坡度;沿XS轴方向的速度vx为竖直速度;沿ZS轴方向的速度vy为水平速度;空间全局坐标系依次绕ZS-XS-YS轴旋转到与质心控制坐标系平行位置时绕ZS轴、XS轴、YS轴的旋转角分别为ψ、φ、θ。
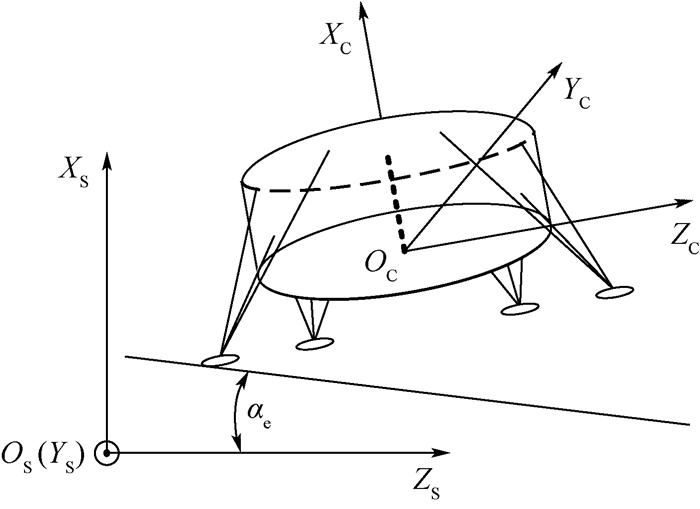 |
| 图 2 坐标系定义 Fig. 2 Definition of coordinate system |
| 图选项 |
1.2 着陆缓冲机构动力学建模
1.2.1 辅助支柱缓冲机构建模 辅助支柱由外筒、内筒及内部吸能材料组成,吸能材料为塑性变形材料。建模时,用外筒和内筒之间移动副的相对位移d描述吸能材料的缓冲行程,用吸能材料提供缓冲力FH的做功描述冲击能量的耗散。缓冲力FH由外筒与内筒之间的相互作用力来描述,其值为关于缓冲行程d的函数,根据吸能材料的力学特性,利用图 3所示的曲线来描述FH与d的函数关系,并通过Spline函数给内外间施加相互作用力进行模拟。
 |
| 图 3 辅助支柱缓冲特性曲线 Fig. 3 Load-stroke characteristic curve of secondary strut |
| 图选项 |
1.2.2 主支柱缓冲机构建模 主支柱采用的缓冲方式与辅助支柱不同。图 4(a)、(b)分别为缓冲杆及与其对应的主支柱示意图[11]及缓冲杆变形特性曲线,M为缓冲杆提供的缓冲力矩值,Se为缓冲杆轴向变形位移值,γ为缓冲杆等效变形转角值。缓冲杆为固连于主体的悬臂梁,当主支柱受载时,缓冲杆亦受力发生弯曲。弯曲最初为弹性变形,但随着负载增加而使材料超出屈服极限时将变为塑性变形。
 |
| 图 4 缓冲杆示意图[11]及其特性曲线 Fig. 4 Schematic diagram of load limiter[11] and its characteristic curves |
| 图选项 |
缓冲杆的动力学模型采用文献[14]提出的刚体等效方法建立。利用有限元软件建立缓冲杆力学模型,输出力矩和转角、力矩和位移之间的关系如图 4所示,而后利用样条曲线拟合方法添加相应缓冲模型。
1.3 足垫与星球表面接触模型 本文采用接触力模型模拟足垫与星球表面的相互作用。足垫接触点和着陆面间的接触作用力分解为法向碰撞力和切向摩擦力2个部分。
法向碰撞力Fn利用非线性弹簧阻尼模型模拟,根据Hertz理论及文献[15]的研究,其力学方程为
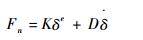 | (1) |
式中:K为接触刚度;e为非线性指数;D为阻尼系数;δ为接触时产生的相对穿透量。
切向摩擦力Ff采用库仑摩擦模型模拟,其一般形式如下:
 | (2) |
式中:μf为足垫与着陆面间动摩擦系数。
2 发动机推力控制模型 2.1 触地关机方案 非零高度关机软着陆方案是指腿式着陆器的足垫底面相对着陆面的高度不为零时的一种发动机关机方案。在非零高度关机出现异常而未能及时关闭主发动机时,探测器在下落过程中将受到尾喷产生的持续“地面效应”,严重影响软着陆稳定性[12];同时被尾喷羽流激起的星球表层沙尘也可能影响探测器正常工作甚至引起主发动机爆燃[13]。为了保证主发动机可靠关闭,采用通过高度关机敏感器发出信号关机(非零高度关机)和足垫接触星球表面发出信号关机(触地关机)2种关机手段。若非零高度关机方案出现异常,则由触地关机方案承担关机任务,提高软着陆稳定性。
触地关机方案通过足垫上安装的触地敏感器感知触地动作,发出触地信号以关闭主发动机。考虑主发动机的减速作用及速度监测、控制存在的偏差,在足垫触地时刻探测器的竖直速度范围在1~ 2 m/s。
2.2 变推力发动机推力控制模型 新型探测器采用7 500 N变推力火箭发动机为主发动机,其推力变比为5:1,能够实现1 500~7 500 N的大范围推力调节[16]。主发动机控制频率为1 Hz,每经过1 s燃料流量调节系统根据当前各个传感器反馈的探测器状态参数,由式(3)所示的推力调节函数计算得当前所需推力大小,控制燃料流量从而实现对主发动机推力的负反馈调节[16]。
 | (3) |
式中:F为主发动机推力;m为探测器总质量;g为星球表面重力加速度;FCi为C系列姿控推进器推力,将在2.3节具体介绍。
根据主发动机推力调节函数及控制过程,在探测器动力学模型的质心位置添加沿质心控制坐标系XC方向的力矢量。建立实时测量项以不断获取探测器的位姿参数,根据式(3)计算所得值改变推力大小。
假设成功触发关机的足垫触地时刻为t0,控制系统接收到触地信号后发出关机指令的时刻为t1,发动机推力开始下降的时刻为t2,姿控推进器关闭时刻为t3,发动机推力下降至0(完成熄火)的时刻为t4,且一旦启动熄火进程其推力将不通过控制系统进行调节[17]。若第1个足垫的触地开关未能触发,则控制系统感知的“触地时刻”t0为第2个触地时刻。着陆过程中,发动机推力的“地面效应”等同于在探测器平台下表面发动机安装位置处(探测器质心处)沿质心控制坐标系XC正方向始终作用有推力F。图 5为第2个足垫触地关机情况下推力F的变化过程示意图。
 |
| 图 5 软着陆阶段主发动机推力控制过程 Fig. 5 Main engine thrust control process during soft landing |
| 图选项 |
2.3 姿控推进器推力控制模型 触地关机软着陆过程中,由于主发动机推力的作用,会产生附加的竖直与水平初速度,增大了软着陆不稳定性[13, 18]。为了保证探测器可靠软着陆,在触地关机方案中引入姿控策略。
姿控推进器点火逻辑模型指着陆过程中各个姿控推进器的点火时机及相应施加的推力大小。由姿控分系统感知探测器当前倾转角及角速度,并根据这些参数调整推进器的作用力及作用时长,从而实现反馈控制,保持探测器姿态稳定。10台推进器对应的推力控制方程如式(4)~式(6)所示。
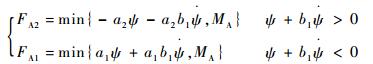 | (4) |
 | (5) |
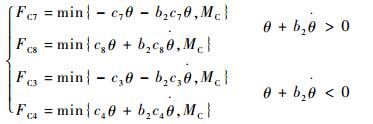 | (6) |
式中:FAi为A系列姿控推进器的推力;ai、bi、ci均为常数,其值根据文献[16-17]确定;MA、MC分别为A、C系列发动机可调节的最大推力值。
姿控推进器的控制频率与主发动机相同。在探测器仿真模型相应位置添加相应方向的力矢量以模拟各个推进器的推力;建立测量项实时监测软着陆仿真过程中相关的位姿参数;后根据函数式及测量计算所得值改变推力大小。
3 着陆初始条件及稳定性判据 3.1 着陆初始条件 如图 2所示,以探测器首个足垫触地时刻开始仿真,软着陆分析过程中探测器倾倒或探测器趋于静止则终止仿真。着陆初始条件参数的分布规律如表 1所示[7], μ、σ分别为正态分布的均值和标准差,min、max分别为均匀分布的上下限值,α、β分别为Weibull分布的形状参数和尺度参数。
表 1 着陆初始条件参数分布[7] Table 1 Parameter distribution of initial landing conditions[7]
| 参数 | 分布 |
| vx/(m·s-1) | N(μ=1.5, σ=0.15) |
| vy/(m·s-1) | N(μ=0, σ=0.33) |
| ψ/(°) | N(μ=0, σ=1.0) |
| φ/(°) | U(min=0, max=45) |
| μf | U(min=0.3, max=0.8) |
| αe/(°) | W(α=5.608, β=1.717) |
表选项
3.2 着陆稳定性评判指标 本文主要研究变推力发动机模型及姿控模型对探测器软着陆稳定性的影响,综合考虑选取以下评判指标。
1) 探测器软着陆过程中不倾倒。将过两相邻足垫中心且平行于重力方向的平面定义为翻倒墙[9],若探测器质心超出4个翻倒墙围成的区域,重力矢量将不再对探测器动力学起稳定作用,则认为探测器倾倒。
2) 着陆倾转角在允许范围内。考虑对探测车的释放和太阳能电池采光效率的影响,探测器稳定着陆后,其主体与着陆面间夹角及探测器姿态角φ应不大于许用值。
3) 主发动机在着陆过程中不发生爆燃。尾喷羽流激起外星球表层沙尘引起主发动机爆燃的概率难以采用常规方法进行分析,因此引入爆燃可能性指标以表征各因素对主发动机发生爆燃可能性的影响。
影响主发动机爆燃可能性的各因素中,发动机推力越大,则羽流密度越大,激起沙尘的可能性和力度也越大;发动机作用时间越长,激起的沙尘使发动机爆燃失效的可能性越大;尾喷距星球表面距离越近,发动机的作用效果越明显。根据推力、距离与爆燃可能性的关系,构造函数式(7),在仿真过程中持续监测相关参数,输出该函数关于时间t的变化曲线,对f(t)作时间的积分即得到反映爆燃可能性的指标值P[17],如式(8)所示。
 | (7) |
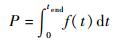 | (8) |
式中:h为尾喷距着陆面距离;tend为仿真终止时间。
4 蒙特卡罗模拟 4.1 采样方法与模拟终止条件 本文结合仿真分析模型,采用蒙特卡罗模拟对探测器软着陆稳定性进行分析。在蒙特卡罗法的抽样环节采用描述性采样方法[19]。描述性采样相比简单随机抽样的优点是:能对同样数量的抽样点提供更好的响应估计,或只需更少的抽样点就可得到同样可信度的响应估计。
蒙特卡罗法的模拟次数是影响其模拟精度和模拟效率的一项重要因素。为了在模拟精度得以满足的同时提高计算效率,本文设定模拟终止准则为:均值估计的相对误差小于设定精度值[7]。
4.2 仿真结果分析 基于4.1节所述方法,分别对发动机未能正常关闭、触地关机方案及带有姿控的触地关机方案下探测器的软着陆稳定性进行了仿真分析。
给定置信水平1-αd=0.99,相对误差为0.05,按照表 1所示各输入变量服从的概率分布模型进行描述性随机采样后依次进行着陆动力学仿真,并记录仿真结果。设定每进行50次蒙特卡罗模拟,对所有仿真分析输出的性能参数进行统计学分析,当所有响应的模拟精度均小于给定值则结束模拟,而后计算出相应的软着陆可靠度。可靠度估计值
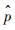
 | (9) |
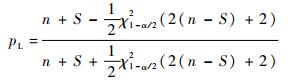 | (10) |
 | (11) |
式中:n为蒙特卡罗模拟总次数;S为稳定着陆的次数;χα2(v)为自由度为v的χ2分布的αd分位点。
仿真分析算例配置情况及分析结果分别如表 2、表 3所示。
表 2 仿真算例配置 Table 2 Configuration of simulation examples
| 算例 | 发动机控制模型 | 模拟的着陆方式 |
| 1 | 主发动机不关闭 | 主发动机关闭失败 |
| 不添加姿控推力 | ||
| 2 | 首个触地足垫触发关机 | 触地关机着陆方案 |
| 不添加姿控推力 | ||
| 3 | 首个触地足垫触发关机 | 带姿控触地关机着陆方案 |
| 添加姿控推力 | ||
| 4 | 第2个触地足垫触发关机 | 带姿控触地关机着陆方案 |
| 添加姿控推力 | 下首个触地足垫触发失败 |
表选项
表 3 仿真结果对比 Table 3 Comparison of simulation results
| 仿真结果 | 算例1 | 算例2 | 算例3 | 算例4 |
| 触发足垫 | 1 | 1 | 2 | |
| 姿控 | × | × | √ | √ |
| 模拟次数 | 600 | 900 | 2 600 | 1 500 |
| 翻倒数 | 84 | 86 | 19 | 8 |
| 倾转角超标数 | 34 | 8 | 25 | 11 |
| P的均值 | 12.23 | 3.39 | 2.26 | 2.28 |
| P的精度 | 0.041 | 0.023 | 0.020 | 0.027 |
| 可靠度估计值 | 0.803 | 0.896 | 0.983 | 0.987 |
| 99%置信区间 | [0.758, 0.844] | [0.867, 0.920] | [0.975, 0.989] | [0.978, 0.994] |
| ??注:×表示未进行姿控;√表示进行姿控。 | ||||
表选项
对模拟结果进行对比分析可知:相较于算例1,算例2的着陆可靠度提升了11.6%,触地关机方案可一定程度改善延时关机故障发生后的探测器软着陆稳定性;对比算例2与算例3可知,引入姿控策略则将稳定着陆可靠度由0.896进一步提高至0.983;且根据算例4的模拟结果,在首个足垫触发器故障而由第2个触地足垫发出关机指令时亦可以得到0.987的着陆可靠度。
由此可见,配备姿控的触地关机方案能够在高度关机方案发生异常时有效提高探测器的着陆稳定性。
5 结论 1) 建立了一种腿式深空探测器的动力学分析模型,采用刚体等效方法模拟塑性变形部件,并针对触地关机着陆方案建立了包括7 500 N变推力发动机与姿态调整推进器的推力控制模型。
2) 利用蒙特卡罗模拟分别对探测器在发动机延时关机、触地关机着陆方式以及带有姿态控制的触地关机着陆方式下的软着陆稳定性进行了分析。分析过程采用描述性采样方法抽取样本点,并基于均值估计相对误差建立蒙特卡罗模拟终止准则,在保证模拟精度的同时提高仿真计算效率。
3) 根据模拟结果计算了探测器在着陆条件不确定下稳定着陆的可靠度。经过对比分析,触地关机方案在高度关机异常时能够改善探测器的着陆稳定性;姿控对提高着陆稳定性亦有积极作用;姿控与触地关机方案的配合工作可进一步提升着陆稳定性。
参考文献
| [1] | 高滨. 火星探测器着陆技术[J].航天返回与遥感, 2009, 30(1): 1–9. GAO B. Mars exploration entry, descent and landing technologies[J].Spacecraft Recovery & Remote Sensing, 2009, 30(1): 1–9.(in Chinese) |
| [2] | 李萌. 腿式着陆缓冲装置吸能特性及软着陆过程动力学仿真研究[D]. 哈尔滨: 哈尔滨工业大学, 2013: 2-18. LI M. Research on energy absorbers of legged-type lander and dynamic simulation on its soft landing process[D]. Harbin: Harbin Institute of Technology, 2013: 2-18(in Chinese). |
| [3] | 朱汪, 杨建中. 月球探测器软着陆机构着陆稳定性仿真分析[J].宇航学报, 2009, 30(5): 1792–1796. ZHU W, YANG J Z. Touchdown stability simulation of landing gear system for lunar lander[J].Journal of Astronautics, 2009, 30(5): 1792–1796.(in Chinese) |
| [4] | 蒋万松, 黄伟, 沈祖炜, 等. 月球探测器软着陆动力学仿真[J].宇航学报, 2011, 32(3): 462–469. JIANG W S, HUANG W, SHEN Z W, et al. Soft landing dynamics simulation for lunar explorer[J].Journal of Astronautics, 2011, 32(3): 462–469.(in Chinese) |
| [5] | 陈金宝, 聂宏, 万俊麟. 深空探测着陆器数字化设计及着陆性能影响因素[J].航空学报, 2014, 35(2): 541–554. CHEN J B, NIE H, WAN J L. Digital design and landing performance influence factors of deep space lander[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 541–554.(in Chinese) |
| [6] | LAVENDER R E. Monte Carlo approach to touchdown dynamics for soft lunar landings: NASA-TN-D-3117[R]. Washington, D. C. : NASA, 1965. |
| [7] | 宋顺广, 王春洁. 基于蒙特卡罗法的月球探测器着陆稳定性分析[J].北京航空航天大学学报, 2013, 39(9): 1192–1196. SONG S G, WANG C J. Landing stability analysis of the lunar lander based on Monto Carlo approach[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(9): 1192–1196.(in Chinese) |
| [8] | 丁建中, 王春洁, 王家俊, 等. 着陆工况对月球探测器着陆缓冲性能影响分析[J].载人航天, 2016, 22(1): 132–137. DING J Z, WANG C J, WANG J J, et al. Effects of touchdown conditions on the buffering performance of the lunar lander[J].Manned Spaceflight, 2016, 22(1): 132–137.(in Chinese) |
| [9] | MERCHANT D H, SAWDY D T. Monte Carlo dynamic analysis for lunar module landing loads[J].Journal of Spacecraft and Rockets, 1971, 8(1): 48–55.DOI:10.2514/3.30216 |
| [10] | ZUPP G A, DOIRONH H. A mathematical procedure for predicting the touchdown dynamics of a soft-landing vehicle: NASA-TN-D-7045[R]. Washington, D. C. : NASA, 1971. |
| [11] | MURACA R J, CAMPBELL J W, KING C A. A Monte Carlo analysis of the viking lander dynamics at touchdown: NASA-TN-D-7959[R]. Washington, D. C. : NASA, 1975. |
| [12] | DOIRON H H, ZUPP G A. Apollo lunar module landing dynamics[C]//41st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 2nd Exhibit. Reston: AIAA, 2000: 1-11. |
| [13] | 吴建云, 王春洁, 宋顺广. 月球探测器典型故障模式分析[J].宇航学报, 2014, 35(6): 633–638. WU J Y, WANG C J, SONG S G. Analysis of typical failure modes for lunar lander[J].Journal of Astronautics, 2014, 35(6): 633–638.(in Chinese) |
| [14] | 吴宏宇, 王春洁, 丁建中, 等. 基于多工况的新型探测器软着陆性能优化[J].北京航空航天大学学报, 2017, 43(4): 776–781. WU H Y, WANG C J, DING J Z, et al. Soft landing performance optimization for novel lander based on multiple working conditions[J].Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(4): 776–781.(in Chinese) |
| [15] | NOHMI M. Modeling for lunar lander by mechanical dynamics software[C]//AIAA Modeling and Simulation Technologies Conference and Exhibit. Reston: AIAA, 2005: 64-73. |
| [16] | 雷娟萍, 兰晓辉, 章荣军, 等. 嫦娥三号探测器7500 N变推力发动机研制[J].中国科学:技术科学, 2014, 44(6): 569–575. LEI J P, LAN X H, ZHANG R J, et al. The development of 7500N variable thrust engine for Chang'E-3[J].Science China:Technology, 2014, 44(6): 569–575.(in Chinese) |
| [17] | WU H Y, WANG C J, DING J Z, et al. Dynamics simulation analysis for novel lander based on two kinds of landing mode[C]//20179th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA). Piscataway, NJ: IEEE Press, 2017: 8-12. |
| [18] | 严立, 王平阳, 欧阳华. 月面环境发动机羽流冲击力效应模拟计算[J].上海交通大学学报, 2012, 46(8): 1310–1314. YAN L, WANG P Y, OUYANG H. Simulation of plume impingement effects in the lunar lander environment[J].Journal of Shanghai Jiaotong University, 2012, 46(8): 1310–1314.(in Chinese) |
| [19] | SALIBY E. A better approach to Monte Carlo simulation[J].Journal of the Operational Research Society, 1990, 41(12): 1133–1142.DOI:10.1057/jors.1990.180 |
