Dutton和Coverdill[3]对容腔充放气过程进行了试验研究,对比了在不同的容腔体积和进出口喷嘴面积下的试验数据与容腔绝热模型计算结果,并分析了产生差异的原因。Thorncroft等[4]通过试验修正容腔内气体多变过程的多变指数来实现容腔内压力、温度响应规律与试验数据吻合,说明容腔内气体历经的是非确定过程,既不是等温过程也不是绝热过程,但未研究气体与容腔壁面换热的影响作用。文献[5-7]则主要分析容腔壁面带有离散热源的封闭容腔内的自然对流过程中的流动与换热特征,缺乏对于带有换热过程的容腔充放气过程的研究。Owczarek和Progelhof[8]对带有喷嘴的圆柱筒容器快速放气过程进行了试验研究,表明在不考虑容器内换热和耗散的情况下,试验和计算结果差异主要来自喷嘴内边界层的影响,说明喷嘴对于容腔的瞬态响应也有影响。Chow等[9]应用了速矢变换的方法研究了带有轴向对称可控阀门的容腔放气问题。上述对于容腔的理论和试验研究中没有考虑容腔的热边界,缺乏对换热影响的分析,未针对容腔建立真实响应模型。传统容腔建模方法一般采用绝热假设,然而在航空发动机中不存在完全绝热的容腔,而且数据表明容腔换热使得充放气响应时间较绝热过程增加[3],说明容腔换热的影响显著,需要在发动机瞬态空气系统分析中充分考虑,但目前用于分析瞬态空气系统的流体网络法中缺少容腔换热模型的支撑。
在航空发动机中存在多种通气形式的容腔,如单孔、单进单出、单进多出和多进多出等。其中,单孔形式的容腔在航空发动机CFM56、D30KY-154等型号中均存在[10],单孔作为卸压孔,可防止容腔内压力变化剧烈造成周围结构失稳。单孔形式容腔无论对发动机空气系统瞬态演化过程,还是在维持结构稳定性方面,都起到很大作用。此外,单孔容腔结构简单,可在此基础上对其他形式容腔展开研究。本文重点研究单孔形式的容腔,建立非绝热单孔容腔零维瞬态模型。
1 理论分析 1.1 基本假设 Horlock和Woods[11]全面分析了容腔充放气过程的热力学特征,如果容腔充放气过程迅速,可近似认为是绝热过程,缓慢则可近似认为是等温过程。在实际过程中,绝热模型或等温模型都不能准确地描述腔内气体的变化过程。
在容腔充放气的过程中,实际腔内的压力和温度分布不均匀,但是容腔三维特征并不明显,本文针对非绝热单孔容腔充放气过程建模,提出如下假设:
1) 容腔时间尺度参数满足τtotal
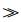
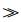
2) 腔内气体状态可集总假设,即假设在瞬变过程中腔内气体速度足够低,容腔内气体参数分布足够均匀,容腔状态只与时间有关,而与空间无关,可用平均状态参数表示[12]。
3) 腔内气体常物性假设,即容腔内气体物性不随气体热力状态变化[12]。
1.2 控制方程 对于理想气体从上游总压到下游静压的一维等熵可压缩膨胀过程,理论流量可以表示为[13]
 | (1) |
式中:W为气体流量;A为流通截面积;ρ为气体密度;p*和p分别为气体上游总压和下游静压;κ为绝热指数。式(1)适用范围为亚声速流动工况。
非定常流动的质量方程[14]为
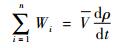 | (2) |
非定常流动的能量方程为
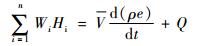 | (3) |
式中:Wi为容腔进出口气体流量;Hi为进出口气体焓;对于本文研究的单孔容腔,n=1;V为容腔体积;e为气体内能;Q为气体与容腔壁面对流换热热流; t为时间。
本文重点关注如何处理气体与容腔壁面的对流换热热流Q,而传统容腔建模方法忽略了换热的影响,对流换热热流表达式为
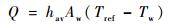 | (4) |
式中:hav为平均对流换热系数;Aw为气体与容腔壁面换热面积;Tref和Tw分别为气体参考温度及壁面温度,这里气体参考温度为腔内气体平均温度。换热控制方程(4)无法表达成解析的形式,因为平均对流换热系数hav通常难以解析表达。
为了解决非绝热单孔容腔零维瞬态模型中换热热流如何处理这一问题,本文综合考虑了影响容腔换热的因素,采用量纲分析推导了单孔容腔换热特性的特征数方程,进而确定热流的大小。
1.3 换热特性 非绝热单孔容腔零维瞬态建模重点是获得壁面对流换热特性,其准确与否直接影响模型的精确性。气体与容腔壁面换热和多个参数相关,为了将高维问题简化,本文针对单孔的容腔形式,采用无量纲分析法[15]推导单孔容腔换热的相似准则及准则方程:
1) 影响单孔容腔壁面对流换热系数h的主要独立参数有:容腔内气体的物性参数(导热系数k、动力黏度μ、气体密度ρ、定压比热容cp)、孔径d(特征长度)、壁面处气流速度u。依据假设认为容腔内建立稳定流场的时间尺度足够小,则壁面处气流速度u与进气速度ui是一一对应的,气体密度ρ是容腔内压力Pv和温度Tv的函数,同时Pv受进气流量ρiAui影响(ρi为进气密度)。本模型几何形式固定,不考虑几何形状参数的影响。综上所述,影响壁面对流换热系数的函数关系式可以写成
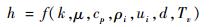 | (5) |
2) 基本量纲:质量M、长度L、时间T和温度Θ。
3) 基本物理量:ui、d、k、μ。
4) 各独立参数的基本量纲见表 1。
表 1 参数量纲 Table 1 Dimension of parameters
| 参数 | 量纲 |
| k | ML/(ΘT3) |
| μ | M/(LT) |
| ρi | M/L3 |
| cp | L2/(ΘT2) |
| d | L |
| ui | L/T |
| Tv | Θ |
| h | M/(ΘT3) |
表选项
5) 分别对定压比热容、进口密度和对流换热系数建立量纲方程,分别得到无量纲数:普朗特数Pr=cpμ/k、进气雷诺数Re=ρiuid/μ和努赛尔数Nu=hd/k,对腔内温度建立量纲方程得到无量纲数:速度系数λ和温比Tv/T0,其中T0为进口总温。
至此,式(5)可转化为
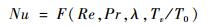 | (6) |
式(6)即为在处理气体与容腔壁面间的换热时所采用的换热特性准则关系式。
针对单孔容腔几何形式,分析了在瞬态响应过程中适用的换热特征数方程,为研究考虑换热影响的非绝热容腔真实响应过程提供基础。对于单进单出等多种其他几何形式容腔均可采用量纲分析方法获取适用不同几何形式容腔的换热特征数方程进行建模。
2 建模方法 首先分析换热对非绝热单孔容腔瞬态响应规律的影响程度,基于此分析讨论如何反映换热影响,显式表达换热项,进而引入换热建立非绝热单孔容腔零维瞬态模型,最后通过CFD数值模拟结果对模型进行对比验证。
第1节给出了非绝热单孔容腔零维瞬态建模的理论分析,明确了建模需求,通过量纲分析推导出与换热特性相关联的准则数,为建模提供了基础。换热特性作为非绝热单孔容腔零维瞬态模型的重要输入,其准确性直接影响模型的准确性。本文从CFD数值模拟中获取影响换热的相关参数,通过整理得到准则数并借助非线性拟合出具体的准则关系式,利用该式显示表达换热项,联立求解质量方程和能量方程得到非绝热单孔容腔零维瞬态响应规律,建模方法如图 1所示。
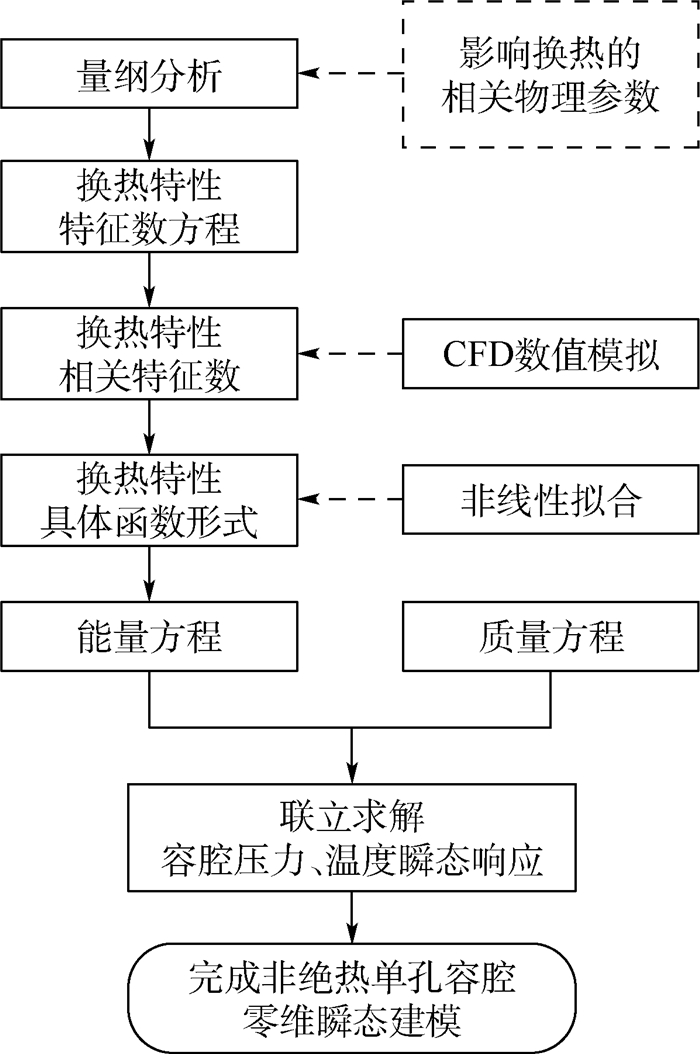 |
| 图 1 非绝热单孔容腔零维瞬态建模方法 Fig. 1 Zero-dimensional transient modeling method of non-adiabatic cavity with single opening |
| 图选项 |
通过与CFD数值模拟结果进行对比验证非绝热单孔容腔零维瞬态模型的准确性。CFD数值模拟本身涵盖了动量方程和能量方程的交互机理,两者耦合求解。在处理容腔问题时,在时间的维度上是非稳态的,在空间的维度上是不均匀的,反映了物理本质和容腔内气体的真实变化,利用CFD数值模拟可以验证在本文研究的时间和空间尺度上模型的准确性。
3 模型计算方法及验证 3.1 计算方法
3.1.1 非绝热单孔容腔零维瞬态模型计算 基于第1节和第2节分析,在Visual C++环境下编制计算程序,建立了非绝热零维瞬态模型(Non-adiabatic Zero-dimensional Transient Model, NZTM)。NZTM首先需要获取几何参数、边界条件、时间步长和模拟总时长,根据初始条件,在不同时刻通过迭代求解控制方程组得到当前时刻容腔内平均压力和温度的响应规律。NZTM具体计算流程如图 2所示。
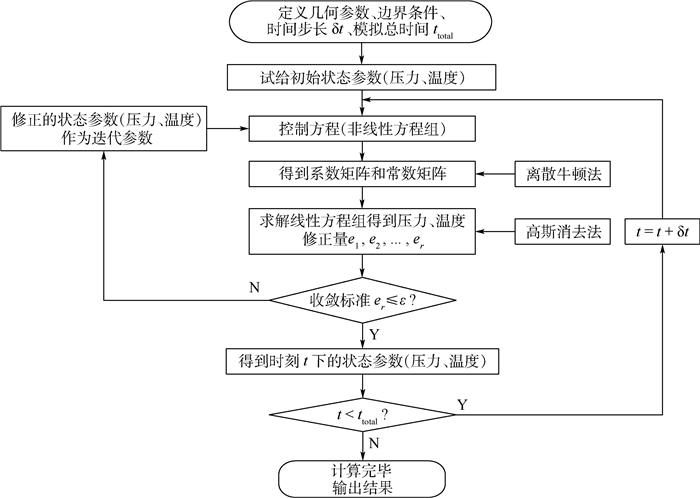 |
| 图 2 非绝热零维瞬态模型计算流程 Fig. 2 Calculation flowchart of non-adiabatic zero-dimensional transient model |
| 图选项 |
为建立NZTM,需要在能量方程中添加气体与容腔壁面间的对流换热项。通过CFD数值模拟获取与换热相关的物理参数,依据本文中给出的处理方式整理出换热特性的具体表达形式,从而支撑模型的建立。
3.1.2 CFD数值模拟 CFD数值模拟一方面提供与换热相关的准则数数据,一方面用于验证模型的准确性。本文针对单孔容腔的充气过程进行验证,因为在该过程中进口气体对腔内气体具有冲击作用,换热较放气过程更明显,选择充气过程更有利于验证非绝热单孔容腔零维瞬态模型的准确性。
容腔物理模型是边长为0.5 m的立方体容腔,壁面边界厚度为0,容腔一侧壁面有直径0.025 m的孔,如图 3所示。
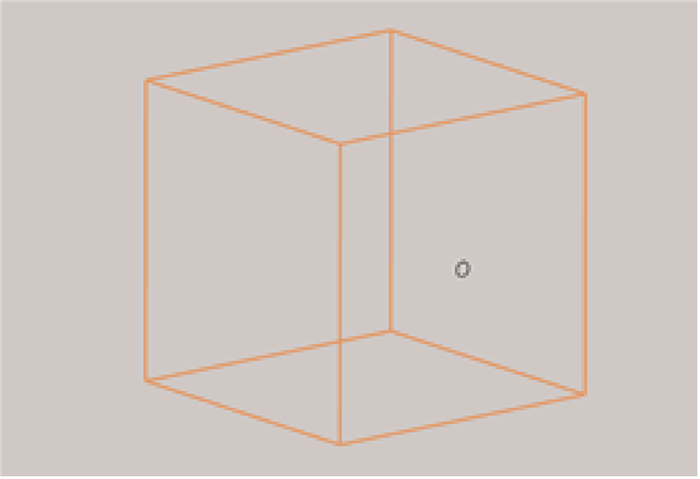 |
| 图 3 容腔物理模型 Fig. 3 Physical model of cavity |
| 图选项 |
采用Fluent计算,模型网格划分如图 4所示,为六面体结构化网格,数量20万,计算采用基于密度的算法进行瞬态求解,控制方程在网格系统上采用有限体积法离散,对流项采取二阶迎风格式,时间项采取一阶隐式差分格式,湍流模型为标准k-ε湍流模型。初始边界(时刻t=0)和计算边界(时刻t>0)条件参数设置见表 2。
 |
| 图 4 数值计算模型网格划分 Fig. 4 Meshing of numerical calculation model |
| 图选项 |
表 2 初始边界和计算边界条件参数 Table 2 Initial boundary and computational boundary condition parameters
| 位置 | 压力/Pa | 温度/K | |||
| t=0 | t>0 | t=0 | t>0 | ||
| 进口 | 101 325 | 191 504 | 288.15 | 288.15 | |
| 壁面 | 323.15 | 323.15 | |||
| 腔内 | 101 325 | 323.15 | |||
表选项
数值计算边界进口为压力进口,压力从101 325 Pa阶跃至191 504 Pa,容腔壁面为等壁温条件。
由特征数方程式(6)可知,直接反映换热特性的努赛尔数Nu与4个准则数相关,在一定条件下可以对该关系式进行简化。
气体密度的静参数和总参数之比的气动函数为
 | (7) |
式中:ρ和ρ*分别为密度的静参数和总参数。
绝能等熵滞止条件下的气体状态方程为
 | (8) |
式中:T*为总温; R为气体常数。
雷诺数Re及速度系数λ的表达式分别为
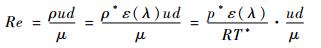 | (9) |
 | (10) |
式中:ccr为临界声速。
将式(9)和式(10)整理可得如下关系式:
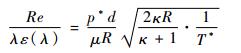 | (11) |
由上述分析可知,在确定的进口初始边界(包括进口总压和总温)及几何条件下,雷诺数与速度系数关系是一一对应的。同时依据常物性假设,普朗特数不变,所以准则关系式(6)可简化为
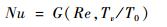 | (12) |
将不同雷诺数Re、温比Tv/T0和对应的壁面平均努塞尔数Nu拟合成函数关系式,各无量纲数关系及拟合数据如图 5所示,拟合数据最大误差不超过2%,拟合得到的特征数方程为
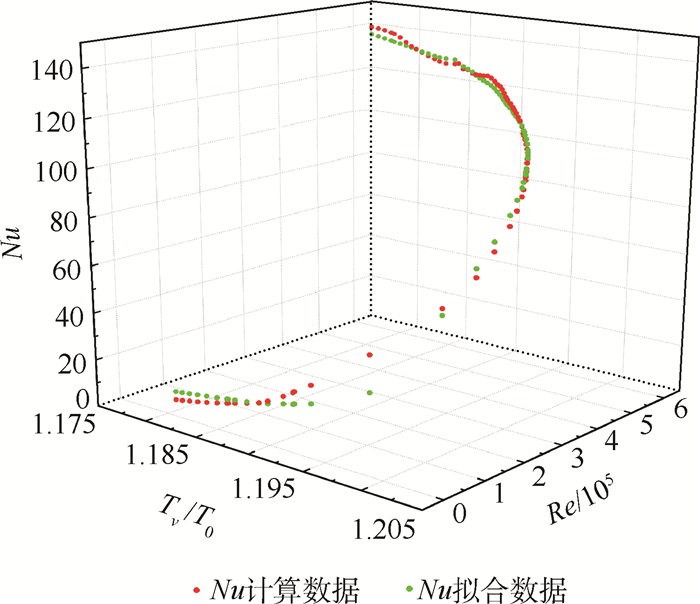 |
| 图 5 无量纲数关系及拟合数据 Fig. 5 Relation of dimensionless number and fitting data |
| 图选项 |
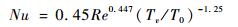 | (13) |
式(13)即对应该容腔几何形式和初始边界条件的换热特性准则关系式。在不同时刻下,根据腔内气体状态及进口气流参数确定唯一的努赛尔数。至此,处理了气体与容腔壁面间的换热,满足了建模需求。
3.2 计算结果对比分析 1) 将NZTM与CFD数值模拟以及绝热模型计算结果进行对比,如图 6所示。
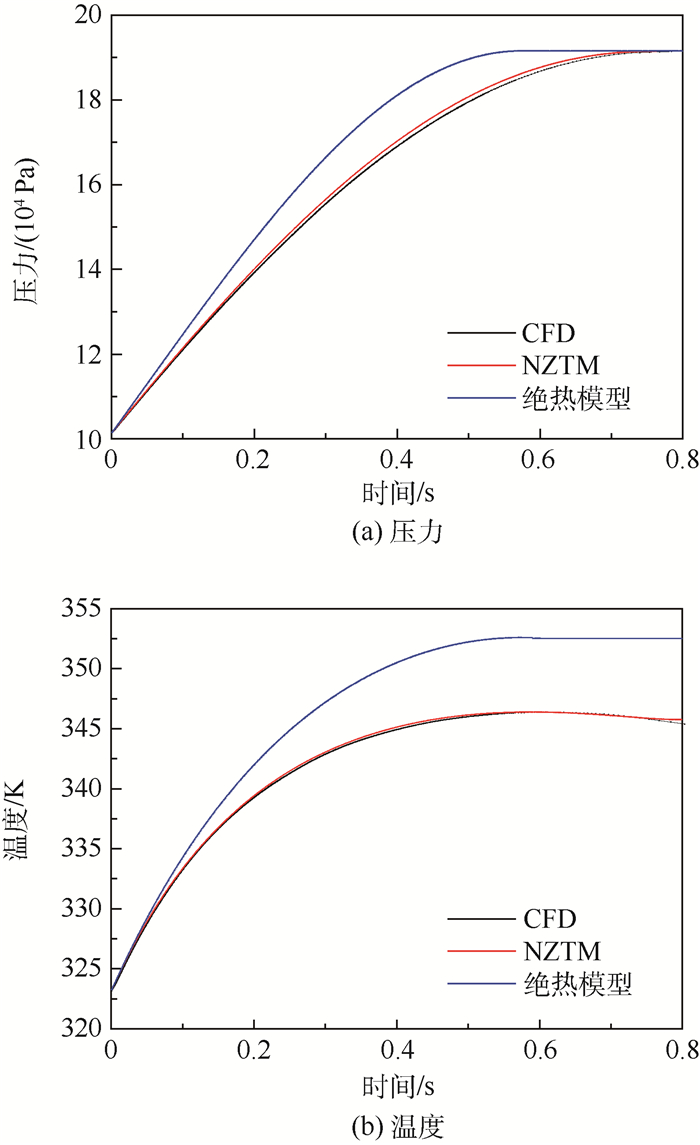 |
| 图 6 CFD数值模拟和NZTM、绝热模型结果对比 Fig. 6 Comparison of results calculated by CFD simulation, NZTM and adiabatic model |
| 图选项 |
可以看出:①在相同的边界条件下,NZTM与CFD数值模拟结果无论在趋势上还是数值上都吻合得很好,两者最大相对误差小于0.8%,如图 7所示。②NZTM与CFD数值模拟结果存在微小偏差,产生偏差的原因:一方面在于NZTM处理换热特性的方式,即将换热特性拟合成准则关系式,而数据拟合本身存在误差;另一方面对于容腔的基本假设也与真实情况存在稍许差别。③非绝热单孔容腔气体压力和温度响应与绝热模型计算结果存在很大差异,其中压力响应的最大相对误差达6%,如图 8所示,这也充分说明了换热对于容腔的瞬态响应有重要影响。同时绝热容腔内气体达到稳定压力所需要的时间较非绝热容腔短,这是因为在容腔充气过程中绝热容腔内气体温度上升更快,在充气过程完成时腔内压力相同,则稳定后绝热容腔内气体密度小,说明绝热过程充气量较少,达到稳定的时间也较短。从温度响应的对比图(见图 6(b))中可以看到非绝热容腔内的气体温度更低,在状态稳定后,温度还有下降趋势,这主要是因为腔内气体与壁面有温差,换热过程还在进行。
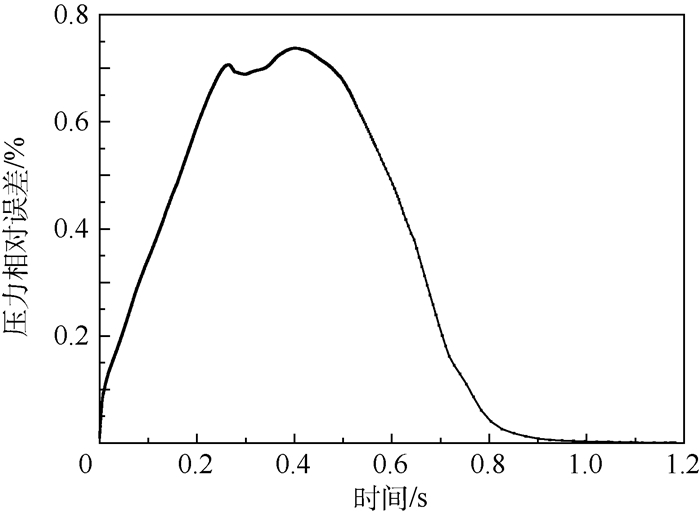 |
| 图 7 NZTM与CFD数值模拟压力的相对误差 Fig. 7 Relative error of pressure between NZTM and CFD simulation |
| 图选项 |
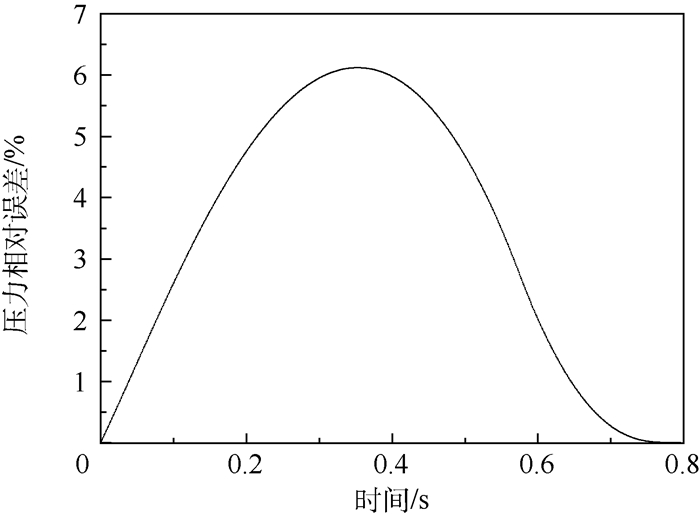 |
| 图 8 NZTM与绝热模型压力的相对误差 Fig. 8 Relative error of pressure between NZTM and adiabatic model |
| 图选项 |
2) 将NZTM与绝热模型和等温模型压力响应进行对比,如图 9所示。
 |
| 图 9 NZTM与等温、绝热模型压力计算结果对比 Fig. 9 Comparison of pressure calculated by NZTM, isothermal and adiabatic model |
| 图选项 |
可以看出:NZTM压力响应曲线介于绝热和等温模型曲线之间。由于响应过程较缓慢,气体与壁面换热充分,所以气体历经过程更接近等温,偏离绝热。三线对比说明了本文建立的NZTM较绝热和等温模型能够更精确地反映单孔容腔内气体真实瞬态响应规律。
4 结论 容腔内气体与腔壁换热对于容腔瞬态响应有重要影响,绝热容腔模型不能精确反映容腔真实响应历程,本文基于此需求建立了非绝热单孔容腔零维瞬态模型(NZTM)。
1) NZTM与CFD数值模拟结果对比最大误差不超过0.8%(绝热模型为6%),表明本文提出的NZTM较绝热模型更好地反映了容腔内气体状态的真实变化。
2) 虽然非绝热单孔容腔的换热特性是通过数值模拟建立的,但是对比结果首先验证了本文对于时间尺度分析的正确性,其次说明了依据本文处理容腔换热的方法,可以复现容腔内气体的真实瞬态响应,体现了准确的换热特性可以保证模型的准确性,精确反映容腔真实瞬态响应。
3) 非绝热零维模型在缩减了3个维度之后,较CFD数值模拟计算量少了数万倍,而精度较高,误差不超过1%,表明方法是可行且有效的。
参考文献
| [1] | SEHRA A K, JR WHITLOW W. Propulsion and power for 21st century aviation[J].Progress in Aerospace Sciences, 2004, 40(4-5): 199–235.DOI:10.1016/j.paerosci.2004.06.003 |
| [2] | 刘传凯, 李圆圆, 李艳茹, 等. 涡轮轴断裂条件下空气系统强瞬变过程分析[J].北京航空航天大学学报, 2016, 42(1): 47–53. LIU C K, LI Y Y, LI Y R, et al. Dynamic analysis of air system with fast transients in shaft failure event[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1): 47–53.(in Chinese) |
| [3] | DUTTON J C, COVERDILL R E. Experiments to study the gaseous discharge and filling of vessels[J].International Journal of Engineering Education, 1997, 13(2): 123–134. |
| [4] | THORNCROFT G, PATTON J S, GORDON R. Modeling compressible air flow in a charging or discharging vessel and assessment of polytropic exponent[C]//ASEE Annual Conference. Honolulu: ASEE, 2007: 1-18. |
| [5] | NARDINI G, PARONCINI M. Heat transfer experiment on natural convection in a square cavity with discrete sources[J].Heat and Mass Transfer, 2012, 48(11): 1855–1865.DOI:10.1007/s00231-012-1026-6 |
| [6] | DENG Q H. Fluid flow and heat transfer characteristics of natural convection in square cavities due to discrete source-sink pairs[J].International Journal of Heat and Mass Transfer, 2008, 51(25-26): 5949–5957.DOI:10.1016/j.ijheatmasstransfer.2008.04.062 |
| [7] | NASSAR N N, MEHROTRA A K. Design of a laboratory experiment on heat transfer in an agitated vessel[J].Education for Chemical Engineers, 2011, 6(3): 83–89.DOI:10.1016/j.ece.2011.06.001 |
| [8] | OWCZAREK J A, PROGELHOF R C. Rapid discharge of a gas from a cylindrical vessel through a nozzle[J].American Institute of Aeronautics and Astronautics, 1963, 1(9): 2182–2183.DOI:10.2514/3.2034 |
| [9] | CHOW W L, TING A A L, TSAI P H. Discharge from a vessel through an axisymmetric control valve[J].Journal of Applied Mechanics, 1987, 54(2): 447–452.DOI:10.1115/1.3173035 |
| [10] | 陈光, 洪杰. 航空燃气涡轮发动机结构[M].北京: 北京航空航天大学出版社, 2010: 170-171. CHEN G, HONG J. Structure of aircraft gas turbine engine[M].Beijing: Beihang University Press, 2010: 170-171.(in Chinese) |
| [11] | HORLOCK J H, WOODS W A. The thermodynamics of charging and discharging processes[C]//Proceedings of the Institution of Mechanical Engineers, London: IMechE, 1965, 180(310): 16-24. |
| [12] | 刘传凯, 刘海明, 李艳茹, 等. 强瞬变空气系统的模块化仿真建模[J].航空动力学报, 2015, 30(8): 1826–1833. LIU C K, LIU H M, LI Y R, et al. Modularized simulation of air system with fast transient[J].Journal of Aerospace Power, 2015, 30(8): 1826–1833.(in Chinese) |
| [13] | 潘锦珊, 单鹏. 气体动力学基础[M].北京: 国防工业出版社, 2011: 87-90. PAN J S, SHAN P. Fundamentals of gasdynamics[M].Beijing: National Defense Industry Press, 2011: 87-90.(in Chinese) |
| [14] | 骆广琦, 桑增产, 王如根, 等. 航空燃气涡轮发动机数值仿真[M].北京: 国防工业出版社, 2007: 84-86. LUO G Q, SANG Z C, WANG R G, et al. Numerical methods for aviation gas turbine engine simulation[M].Beijing: National Defense Industry Press, 2007: 84-86.(in Chinese) |
| [15] | 邹滋祥. 相似理论在叶轮机械模型研究中的应用[M].北京: 科学出版社, 1984: 17-24. ZOU Z X. Application of similarity theory in turbomachinery model[M].Beijing: Science Press, 1984: 17-24.(in Chinese) |
