变循环发动机本身结构复杂,在传统双轴涡扇发动机部件级模型的基础上,需要引入核心驱动风扇级和可变面积涵道等,因此变循环发动机的共同工作方程需要适应新的部件气路平衡,双外涵与单外涵的变气路特性便增加了非线性模型建立的难度。现在常用的非线性模型求解方法有:牛顿-拉夫逊(Newton-Raphson)法、N+1残量法,以及其他优化算法等。而上述传统方法虽然能够满足位于初值方程解附近邻域的快速收敛,但无法保证全局收敛性,对初值具有较强的依赖性。其中,Newton-Raphson法需要在迭代每一步中多次进行发动机部件特性迭代和雅可比矩阵的求解,导致计算量很大。此外,现代优化算法中所提出的粒子群优化(Particle Swarm Optimization, PSO)算法、遗传算法(Genetic Algorithm,GA)和反向传播(Back Propagation,BP)神经网络算法等虽具有高概率的全局收敛性,但求解效率很低,无法满足发动机模型求解的实时性。当前,越来越多的科研人员关注航空发动机部件模型求解问题且取得了一定的成果。文献[12-13]分别提出了基于GA及混合GA的发动机模型求解方法。该方法与传统方法相比,改善了求解收敛性,但运算量依旧过大,且求解效率较低。文献[14]将BP神经网络算法与Newton-Raphson法结合,在一定程度上提高了模型的求解效率,改善了收敛性,但神经网络对样本训练要求高,训练样本不易获得,并且对于复杂的优化问题,算法极易陷入局部极小值。文献[15-16]分别提出了基于粒子群算法与N+1残量法、Newton-Raphson法的混合粒子群算法,有效地解决了求解效率问题,但其中所采用的传统粒子群算法收敛性较差,无法达到发动机的实时性要求且求解过程中容易陷入局部最优解。关于混合算法仍有很多研究成果,文献[17]提出了一种基于改进后PSO算法和Newton-Raphson法混合算法,但PSO算法随机性不高,并且不能保证以概率1收敛至全局最优。此外,该算法未进行2种算法混合的结点做实时判断,可能会使粒子群算法迭代的次数过多,从而降低求解效率。因此,为改善上述求解中遇到的问题,基于量子粒子群优化(Quantum PSO, QPSO)算法和Broyden拟牛顿法的优点,提出了基于发散系数作为切换条件的混合算法方案,并将该方法应用于VCE(本文所研究的均指核心驱动风扇级(Core Drive Fan Stage, CDFS)双涵道VCE,下文统称为变循环航空发动机)的部件模型建模中。
1 问题描述 VCE部件级稳态和过渡态总体性能模型的收敛性主要取决于如下几个因素:①初值的影响;②控制规律的影响;③部件特性的影响。VCE模型求解问题可看作一类有约束的优化问题,优化问题的三要素为:优化变量、约束条件、目标函数。在优化问题求解中,传统的牛顿法及其各种改进方法均为梯度优化法,该类方法全局收敛的条件是目标函数为凸函数和由约束条件限制的可行域为凸集。控制规律与部件特性主要是对可行域范围和凹凸性有影响,进而影响模型求解的收敛性。此外,由于VCE模型平衡方程组为非线性方程组,其目标函数并非严格的凸函数,因此初值的选取对模型求解过程的收敛性有很大的影响。
Broyden拟牛顿法是Newton-Raphson法的一种改进算法,可用于VCE模型平衡方程组的求解,该算法只需在迭代过程的第1步计算雅可比矩阵的特点使得其计算效率高于Newton-Raphson法。Broyden拟牛顿法迭代计算能够收敛的前提是目标函数为凸函数。采用Broyden拟牛顿法进行求解时当自变量误差不均匀或误差较大时会是计算陷入局部最优值或趋于发散,进而导致模型求解过程中初值选取不合理时迭代计算无法收敛到给定精度或迭代中收敛一致性较差。图 1以3阶非线性方程组为例,给出了不同初值选取对Broyden拟牛顿法求解收敛性影响分析,其中xij为第i个初值点下的第j步迭代点。当初值点为x10时迭代陷入局部最优解,初值点为x20时迭代过程发散,初值点为x30时迭代过程收敛。图 2以3阶非线性方程组为例给出了收敛一致性的说明,迭代第3步时趋于发散,误差增大,迭代后期又趋于收敛,即收敛一致性较差。其中,收敛一致性较差会使得发动机模型求解过程中自变量参数易迭代到发动机部件特性图外,即自变量迭代到可行域范围之外,进而使得模型求解无法继续进行。
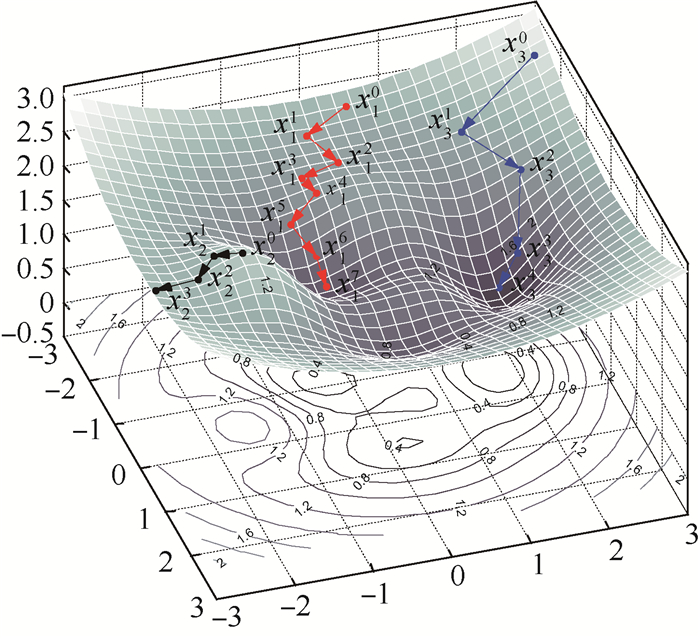 |
| 图 1 初值选取对Broyden拟牛顿法求解收敛性的影响 Fig. 1 Influence of initial value selection on solving convergence of Broyden quasi-Newton method |
| 图选项 |
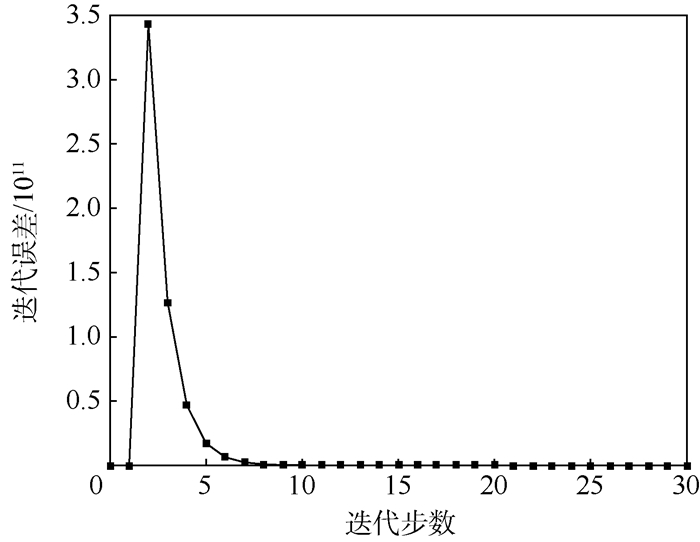 |
| 图 2 初值选取对Broyden拟牛顿法收敛一致性的影响 Fig. 2 Influence of initial value selection on convergence consistency of Broyden quasi-Newton method |
| 图选项 |
基于上述分析,智能优化算法不依赖于目标函数是否为凸函数的特点使其具有全局收敛性,但智能算法迭代计算效率较低的缺点使其不适合直接应用于VCE模型求解计算。利用智能算法的全局收敛性对Broyden拟牛顿法进行改进是一种思路,但是在混合算法的设计中如何平衡智能算法与Broyden拟牛顿法,进而提高混合算法整体计算效率是需要解决的问题。本文给出一种采用QPSO算法对Broyden拟牛顿法进行修正的混合算法,通过引入体现自变量误差均匀性和误差变化趋势的发散系数来判断迭代过程的收敛趋势以提高混合算法的收敛性和收敛一致性。
2 变循环航空发动机非线性模型建模方法 2.1 VCE变几何特性 变循环航空发动机的多个可调几何部件对其性能影响很大,如:压气机可调叶片角度、涡轮导叶可调角度以及其他可调变量,有必要将变几何特性的表征应用于发动机非线性模型中。目前,变几何特性计算方法很多,主要分为已知结构参数的计算方法和未知结构参数的经验公式计算方法。对于VCE而言,国内仍没有相关的结构参数等,需要采用相关变几何特性经验计算方法。参考德国MTU公司开发的燃气涡轮发动机计算软件(GasTurb)软件中的变几何特性的处理方法[18],引入修正系数将求解方法改为
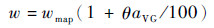 | (1) |
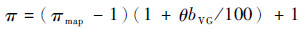 | (2) |
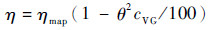 | (3) |
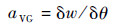 | (4) |
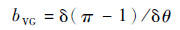 | (5) |
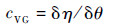 | (6) |
式中:aVG、bVG、cVG分别为质量流量、压比、效率的修正系数,分别反映了导流角度θ对质量流量w、压比π及效率η变化的影响;wmap、πmap、ηmap分别为由发动机部件特性图插值得到的质量流量、压比及效率;δw为质量流量增量、δ(π-1)为压比增量、δη为效率增量;δθ为导流角度增量。由于传统方法取各系数取为定值,而忽视了换算转速变化、性能参数变化对压比和效率的影响。该方法通过引入修正系数实现了变化趋势的改善,从而建立了性能参数随角度的变化率。
由于有限的数据资源,因此,将现有的3组不同角度特性作为数据源,将换算转速和角度变化作为输入,采用多维样条拟合方法提取影响系数的变化规律。首先将已有的变几何角度分别为-26°、0°、16°的3组特性数据作为数据模型,在定转速下求取不同角度对应的质量流量、压比和效率变化率并依次求取各个换算转速的变化率数据。然后采用样条拟合方法分别提取角度变化、换算转速变化时压比、效率以及质量流量影响效率的变化趋势,将一维样条拟合方法实现多维化。最后根据提取换算转速、角度变化时的变化率数据,通过变几何特性计算公式求取各个特性数据。
此处以压气机特性为例,计算可调静子叶片角度为10°时的特性数据。图 3给出了所采用修正方法与传统方法(修正系数K为定值)的对比结果。
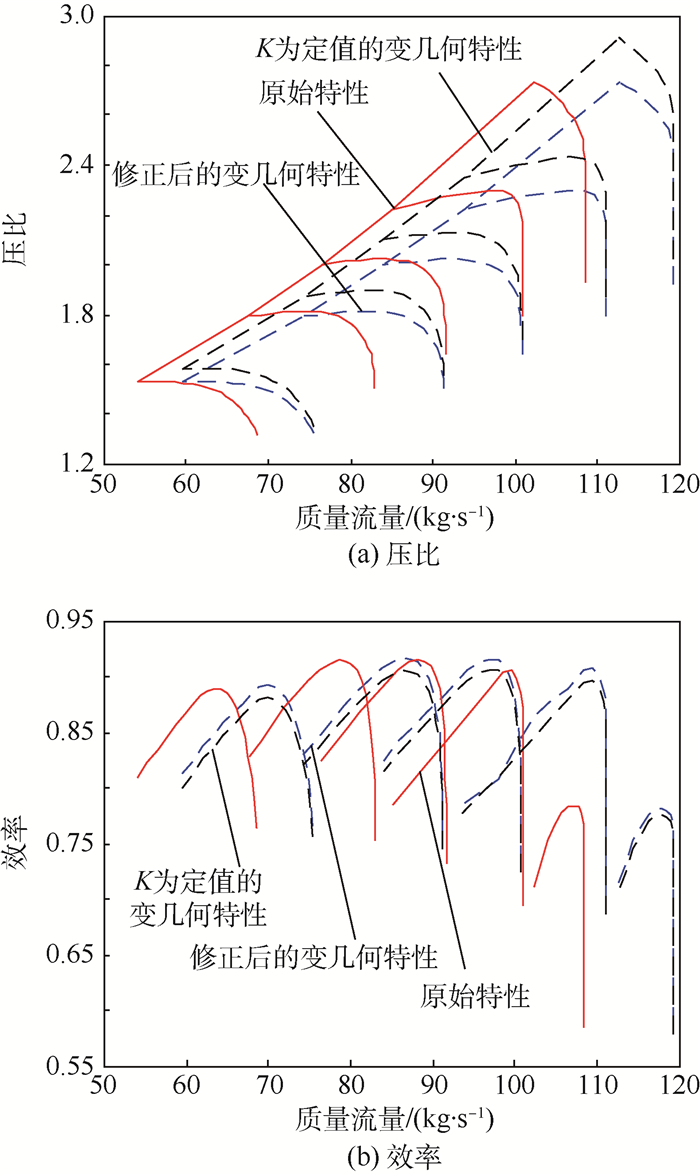 |
| 图 3 可调静子叶片角度为10°时,变几何特性修正计算与传统方法结果对比 Fig. 3 Comparison of variable geometry characteristic correcting calculation results with results of traditional method when adjustable stator blade angle is 10° |
| 图选项 |
由图 3可以看出,正后的压气机特性与传统方法趋势一致,且不同换算转速与角度变化时,变化趋势不同。同时,压气机角度增大时,随着质量流量的增大,压比变化幅度增大。而无论角度开大或关小,效率都是下降的,且程度不一,面积开大的减小量小于面积关小的减少量。
特性数据计算结果为建立反映变几何特性的变循环航空发动机部件模型提供数据基础。同时,采用修正的变几何特性计算方法同样可以用来计算CDFS与可变导向器角度的涡轮等部件特性。
2.2 VCE外涵道特性匹配分析 变循环航空发动机通过调节模式选择活门(Model Select Valve, MSV)、前可调涵道引射器(Front Variable Area Bypass Injector, FVABI)、后可调涵道引射器(Rear Variable Area Bypass Injector, RVABI)的面积来实现外涵与内涵之间的质量流量与静压匹配,这3个活门是影响变循环航空发动机模式切换的重要部件,从而通过气路的重新分配来满足不同工作模式的推力与耗油率需求。图 4所示为外涵道结构示意图。
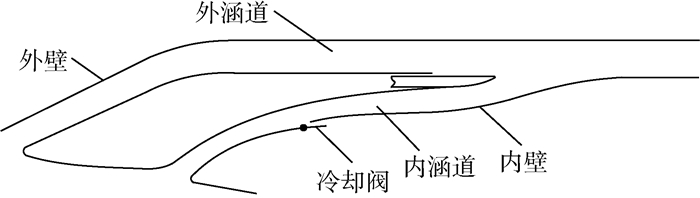 |
| 图 4 变循环航空发动机外涵道结构示意图 Fig. 4 Schematic diagram of external duct structure of variable cycle aero-engine |
| 图选项 |
图 5给出了副外涵的CFD仿真结果。图 5所示为模式选择活门为5°时,进口总压分别为356.24和351.091 kPa工况下的副外涵道与CDFS涵道流场计算结果。由图 5可以看出:①模式选择活门面积一定时,总压恢复系数随着进口总压降低而降低,且降低的趋势更大;②当进口总压维持不变时,模式选择活门开大,流入外涵的质量流量变大,但是总压恢复系数降低,且降低的趋势更大;③当偏离设计点的活门开度时,副外涵的压力损失较大。CDFS涵道的分析方法与副外涵一致。
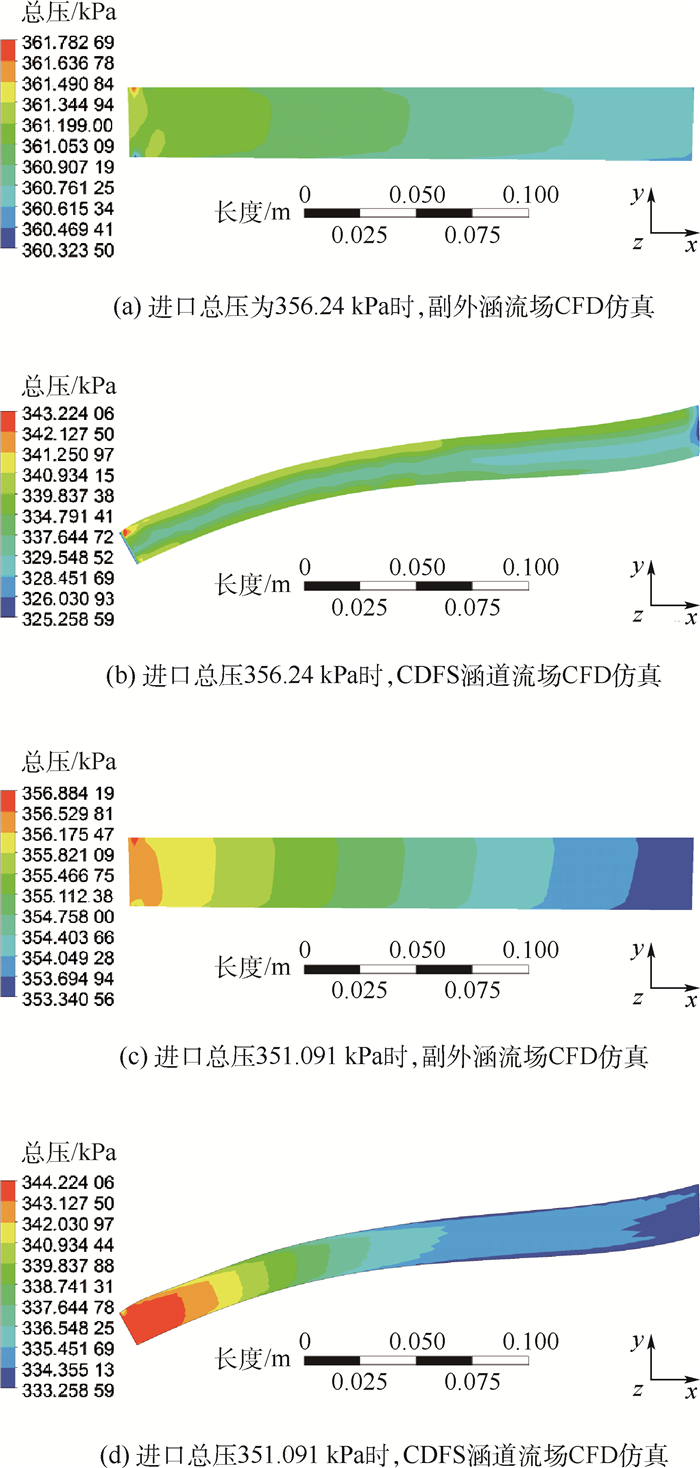 |
| 图 5 模式选择活门为5°时,进口总压分别为356.24和351.091 kPa工况时,副外涵道与CDFS涵道流场计算结果 Fig. 5 Flow field calculation results of vice external duct and CDFS duct at total import pressure of 356.24 and 351.091 kPa when mode of valve 5° is selected |
| 图选项 |
根据流场计算结果,分别将模式选择活门面积、进口气流总压以及静压作为输入,将外涵道的总压损失系数作为目标输出,通过BP神经网络智能映射出函数关系。其中,建立了输入层2层,输出层1层,隐形学习层10层,输出学习层1层的transig函数神经元网络结构。
在上述基础上,进行外涵道模式选择活门角度、进口总压与总压恢复系数的映射函数样本训练,神经网络训练结果如图 6所示。
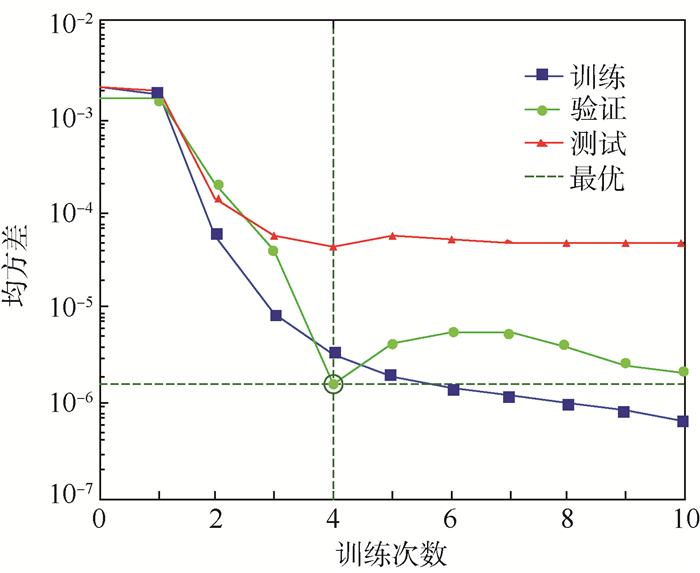 |
| 图 6 神经网络训练结果 Fig. 6 Neural network training results |
| 图选项 |
由图 6可以看出,神经网路训练收敛速度很快且啮合度很高,所采用的BP神经网络能够很好的实现模式选择活门角度、进口总压与涵道总压恢复系数的映射,最终建立的多维映射关系如下:
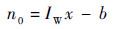 | (7) |
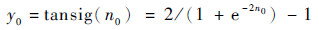 | (8) |
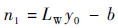 | (9) |
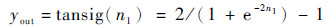 | (10) |
式中:n0和n1分别为隐含层节点、输出层节点;IW和LW分别为隐含层学习参数、输出层学习参数;y0和yout分别为隐含层输出、输出层输出;b为修正参数。
3 基于QPSO的混合算法 3.1 混合算法方案 基于QPSO的混合算法由QPSO算法和Broyden拟牛顿法混合构成。混合算法在非线性方程组迭代求解过程的初期,采用Broyden拟牛顿法进行计算,并通过发散系数判断是否趋于发散。若迭代过程趋于发散则混合算法切换为QPSO算法进行迭代计算,并判断发散趋势。当迭代过程再次趋于收敛时,混合算法切换到Broyden拟牛顿法。反复进行以上过程直到迭代误差达到要求精度时完成计算过程。图 7给出了基于QPSO的混合算法求解方案。基于QPSO的混合算法保留Broyden拟牛顿法超线性的收敛速度,同时采用QPSO算法对其进行优化弥补了Broyden拟牛顿法对初值较依赖且不具有全局收敛性的缺点。同时,通过引入发散系数判断迭代过程的是否趋于发散,并以此为依据实现混合算法中2种算法的合理切换,以降低求解过程中QPSO算法低效性对混合算法整体效率的影响。
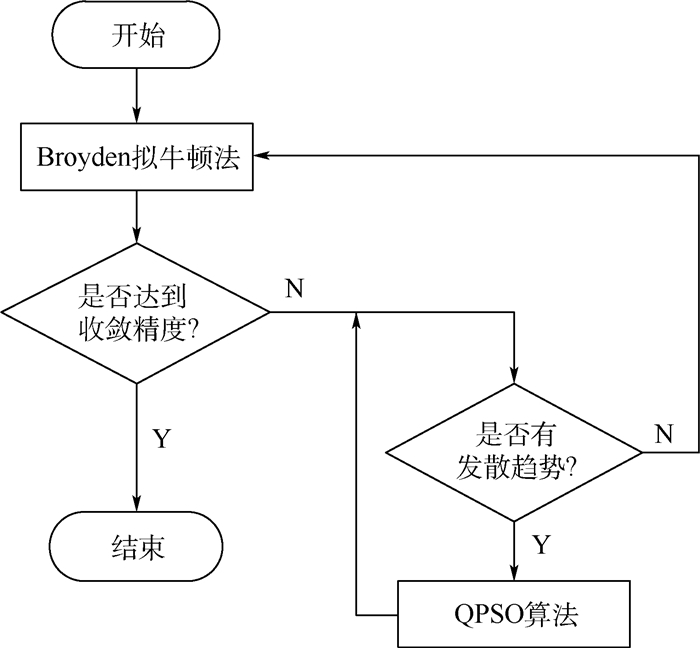 |
| 图 7 基于QPSO的混合算法求解方案 Fig. 7 Hybrid algorithm solution based on QPSO |
| 图选项 |
其中,一般求解时采取Broyden拟牛顿法计算公式如下:
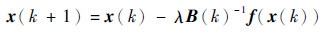 | (11) |
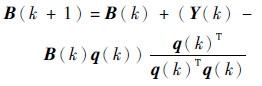 | (12) |
 | (13) |
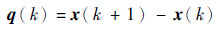 | (14) |
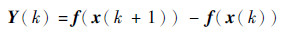 | (15) |
式中:λ为迭代步长,通常取1;x(k)=[x1(k)x2(k) … xM(k)]T为第k代粒子位置; B(k)、f、Y(k)、q(k)分别为修正函数、非线性系统、迭代误差、自变量增量;Jacobi(0)为迭代过程初始状态的雅可比矩阵。
当混合算法判断计算趋于设定的发散边界时,采取QPSO算法,以下具体给出QPSO算法。
设定种群规模为M,进行N维优化问题的求解,公式如下:
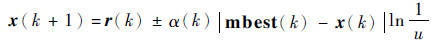 | (16) |
式中:α(k)为第k代的收缩扩张因子,该参数是QPSO算法一个非常重要的参数,该参数设置是否合理直接影响算法性能;u为[0, 1]之间的随机数;mbest(k)为第k代平均最好位置;r(k)=[r1(k)??r2(k)??…??rM(k)]T为第k代时粒子的吸引子,第i个粒子的第k代的吸引子为
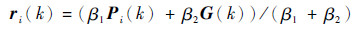 | (17) |
其中:β1、β2为[0, 1]之间的随机数;Pi(k)为第i个粒子的第k代的局部最好位置;G(k)为第k代时的全局最好位置。
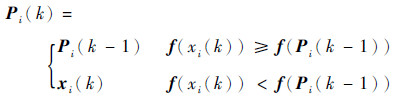 | (18) |
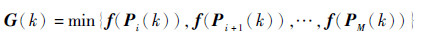 | (19) |
mbest(k)计算公式如下:
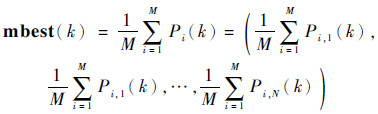 | (20) |
此处针对QPSO算法中的收缩扩张因子给出一种分段线性变化取值策略:
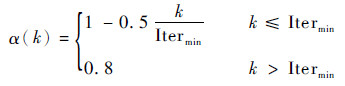 | (21) |
式中:Itermin一般取最大迭代次数的25%左右。
基于上述2种方法,按图 7给出的混合求解方案,依据发散系数对2种求解方法进行混合切换。该发散系数如下:
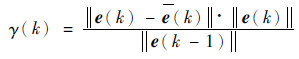 | (22) |
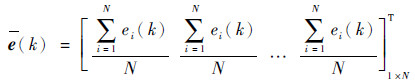 | (23) |
式中:e(k)为第k步迭代误差e(k)=f(x(k));ei(k)为迭代计算第k步自变量第i个分量的误差值。
γ(k)中
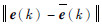
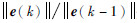
3.2 收敛性及求解效率分析 在不同初始值条件下,基于混合算法、QPSO算法、Broyden拟牛顿法等对某7阶非线性方程组进行求解,其收敛性及求解效率对比结果如图 8所示。
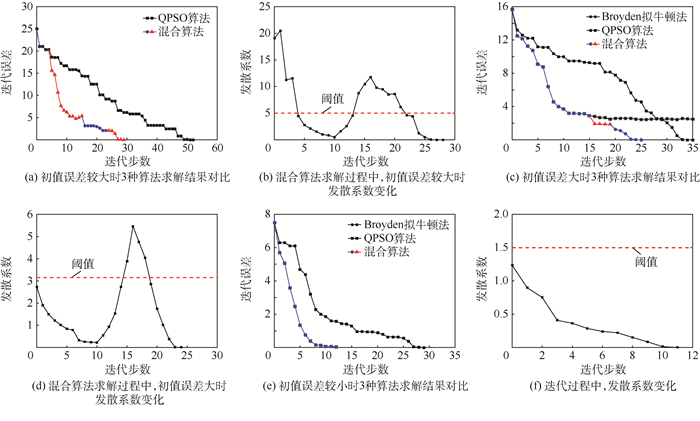 |
| 图 8 高阶非线性方程组求解结果对比 Fig. 8 Comparison of solving results of high-order nonlinear equations |
| 图选项 |
图 8(a)所示的初始误差条件下,给定初值误差较大且不均匀, Broyden拟牛顿法发散,QPSO算法经过52步迭代达到收敛精度,混合算法经过28步迭代达到收敛精度。混合算法迭代过程中发散系数变化如图 8(b)所示,混合算法迭代初期,发散系数较大,超过阈值(初始误差的20%)采用QPSO算法。迭代计算第5步时发散系数减小到小于阈值混合算法切换到Broyden拟牛顿法,由于总误差依然很大,迭代计算到第11步之后发散系数增大并在第15步时超过阈值,迭代过程趋于发散,此时混合算法再次切换到QPSO算法。经过QPSO算法8步迭代,在第23步时发散系数小于阈值,此时混合算法切换到Broyden拟顿法经过6步迭代完成求解过程。
图 8(c)所示的初始误差条件下,在第15步时,Broyden拟顿法陷入局部最优解,QPSO算法经过35步达到误差精度要求,而混合算法经过25步计算达到误差精度要求。图 8(d)可以看出,由于前14步迭代中发散系数小于阈值,因此采用Broyden拟顿法计算。在第15步时发散系数大于阈值,切换至QPSO算法,经过4步迭代发散系数再次小于阈值,此时混合算法再切换到Broyden拟顿法,并经过6步迭代达到收敛要求。
图 8(e)所示给定初始误差下,QPSO算法经过29步迭代达到收敛,混合算法、Broyden拟顿法经过12步迭代达到收敛。在该初值下,混合算法发散系数始终小于阈值,可一直基于Broyden拟顿法进行求解。
通过上述算例表明,基于QPSO的混合算法求解方案通过引入发散系数有效的反映迭代过程的收敛趋势,以此为依据实现算法之间的合理切换,在保证收敛性的同时提高了算法的求解效率。综上所述,提出的混合算法能够有效完成非线性方程组的求解。
4 仿真分析 4.1 初猜值及共同工作方程组选取 VCE在整机建模时,选取以下7个变量作为初猜值:低压转子转速nL、高压转子转速nH、前段风扇压比系数ZF、核心机驱动风扇级压比系数ZCDFS、压气机压比系数ZC、高压涡轮压比系数ZHT、低压涡轮压比系数ZLT。因此,共同工作方程为
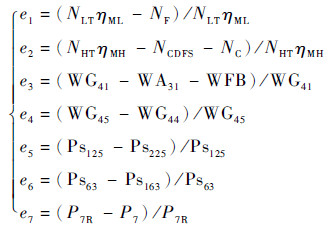 | (24) |
式中:NF、NCDFS、NC为风扇、CDFS、压气机消耗功率;NHT、NLT分别为高压涡轮、低压涡轮输出功率;ηMH、ηML分别为高、低压转子机械效率;WFB为主燃油流量;WA31、WG41、WG44、WG45分别为压气机出口截面空气流量、高压涡轮进口燃气流量、高压涡轮出口燃气流量、低压涡轮进口燃气流量;Ps225、Ps125、Ps63、Ps163分别为副外涵出口静压、CDFS涵道截面静压、后混合室入口内涵静压、混合室入口外涵静压;P7、P7R分别为尾喷管进口总压、尾喷管进口反压。
4.2 基于混合算法的VCE模型验证 将基于QPSO的混合算法应用于VCE模型求解中,迭代误差精度设为10-6。选取的单涵与双涵设计点参数与GasTurb10软件一致,如表 1所示。
表 1 设计点参数 Table 1 Design point parameters
| 参数 | 参数值 | |
| 双涵模式 | 单涵模式 | |
| 低压转子转速PCNF | 100 | 100 |
| 高压转子转速PCNC | 100 | 100 |
| 风扇叶尖压比PRF_tip | 3.5 | 3.5 |
| 风扇叶根压比PRF_root | 3.2 | 3.2 |
| CDFS压比PRCDFS | 1.3 | 1.3 |
| 压气机压比PRC | 6 | 6 |
| 燃烧室总温T4/K | 1850 | 1850 |
| 高压涡轮落压比PRHT | 2.763489 | 2.795642 |
| 低压涡轮落压比PRLT | 1.915404 | 1.703737 |
| 前涵道比BYPASS1 | 0.3 | 0 |
| 后涵道比BYPASS2 | 0.3 | 0.4 |
表选项
图 9为固定燃烧室出口总温条件下,所建立的部件模型与GasTurb10的性能计算结果对比,分别给出了高度特性与速度特性仿真结果,H为高度,Ma为马赫数。从图中可以看出,所建模型的速度特性与高度特性仿真特性变化趋势与GasTurb10性能趋势基本一致,且误差均不大于2%。
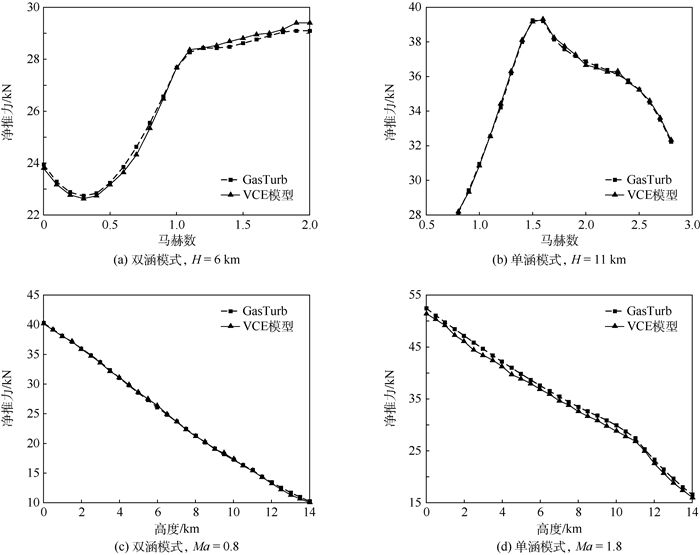 |
| 图 9 双涵及单涵模式下不同高度及马赫数的速度及高度特性仿真结果对比 Fig. 9 Comparison of simulation results of velocity and height characteristics at different height and Mach numbers in double-duct and single-duct modes |
| 图选项 |
仿真结果表明,所提出的混合算法能够实现变循环航空发动机部件模型求解和性能计算,且求解精度满足要求。
4.3 VCE稳态、动态特性分析 通过与GasTurb性能仿真结果的对比验证了所建模型的有效性后,对VCE模型进行性能分析。图 10给出固定高压转子转速时,不同稳态点在单涵工作模式和双涵工作模式的净推力和耗油率性能仿真结果。
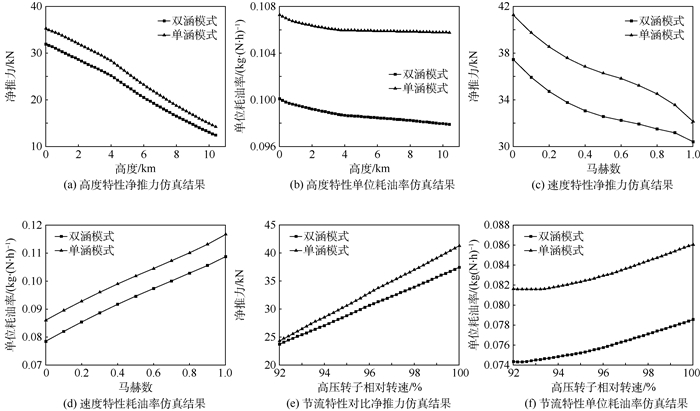 |
| 图 10 单、双涵模式工作VCE稳态特性对比 Fig. 10 Comparison of steady-state characteristics of variable-cycle engines between single-duct and double-duct working modes |
| 图选项 |
图 10所示的仿真结果充分表明,所建立的变循环航空发动机部件模型能够有效反映其不同工作模式的性能。在相同的环境条件下,单涵模式的净推力大于双涵模式;同时,双涵模式燃油消耗小于单涵模式,上述对比充分反映了变循环航空发动机的结构及性能特点。
此外,对变循环航空发动机进行了动态特性仿真分析。图 11给出了H=8 km、Ma=0.9的双涵工作模式仿真结果;图 12给出了H=12 km、Ma=1.5时单涵工作模式仿真结果。其中,控制器采用了比例-积分-微分(Proportion-Integration-Differentiation,PID)控制器(由于研究重点和篇幅限制,此处不过多说明)。
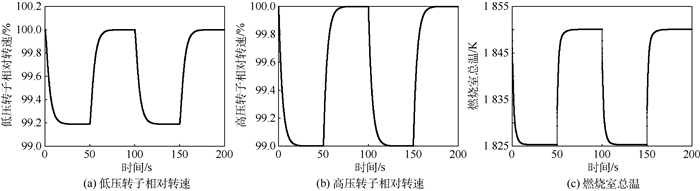 |
| 图 11 H=8 km,Ma=0.9的双涵工作模式动态仿真结果 Fig. 11 Dynamic simulation results of double-duct working mode when H=8 km and Ma=0.9 |
| 图选项 |
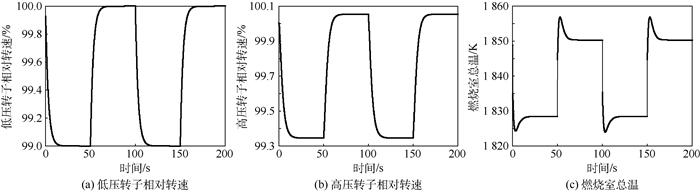 |
| 图 12 H=12 km,Ma=1.5的单涵工作模式动态仿真结果 Fig. 12 Dynamic simulation results of single-duct working mode when H=12 km and Ma=1.5 |
| 图选项 |
图 12可以看出,所建立部件模型能够很好的变循环航空发动机的动态特性,如:亚音速时发动机的双涵工作性能、超音速时发动机的单涵工作性能等。
5 结论 以某型双转子、双涵道混合排气式变循环航空发动机为对象,给出了基于变几何特性修正方法和BP神经网络的部件建模方法,并将基于QPSO的混合算法应用在变循环航空发动机模型的非线性方程组求解中。
1) 完成了对变几何部件的特性分析,同时基于BP神经网络方法建立了外涵道进口压力、活门角度以及总压恢复系数之间的稳态映射关系。
2) 提出了基于QPSO的混合算法求解方案,通过引入发散系数实现混合算法的切换,以改善Broyden拟牛顿法对初值选取的依赖性同时提高混合算法的求解效率。通过对构造的某高阶非线性方程组求解验证算法的有效性和求解效率。结果表明所设计混合算法能够很好的完成非线性方程组的求解。其收敛性优于Broyden拟牛顿法,求解效率高于单一的QPSO算法,且折中考虑的综合性能优于上述2种方法。
3) 对所建立的变循环航空发动机进行了验证并对其性能进行了仿真分析。结果表明:所建立的变循环航空发动机部件模型其高度特性、速度特性与GasTurb仿真结果趋势一直,且误差均不大于2%,符合精度要求。其次,基于混合求解算法所建立的VCE模型能够有效反映其稳态、动态特性,且复合VCE的结构及工作特点。
参考文献
| [1] | 姚艳玲, 黄春峰. 先进变循环发动机技术研究[J].航空制造技术, 2012(23): 106–109. YAO Y L, HUANG C F. Research on advanced variable cycle engine[J].Aeronautical Manufacturing Technology, 2012(23): 106–109.(in Chinese) |
| [2] | 樊思齐. 航空发动机控制[M].西安: 西北工业大学出版社, 2008: 65-68. FAN S Q. Aeroengine control[M].Xi'an: Northwesten Polytechnical University Press, 2008: 65-68.(in Chinese) |
| [3] | KREBS J N, ALLAN R D. Supersonic propulsion-1970 to 1977: AIAA-1977-0832[R]. Reston: AIAA, 1977. |
| [4] | ALLAN R D. General electric company variable cycle engine technology demonstrator program: AIAA-1979-1311[R]. Reston: AIAA, 1979. |
| [5] | FRENCH M W, ALLEN G L. NASA VCE test bed engine aerodynamic performance characteristics and test results: AIAA-1981-1594[R]. Reston: AIAA, 1981. |
| [6] | US Navy instigates variable-cycle engine programme[EB/OL]. [2017-02-21]. Jane's Defence Weekly, 2011. |
| [7] | SIMMONS R J. Design and control of a variable geometry turbofan with an independently modulated third stream[D]. Columbus: The Ohio State University, 2009. |
| [8] | JOHN R. Real-time simulation of F100-PW-100 turbofan engine using the hybrid computer: NASA TMX-3261[R]. Washington, D. C. : NASA, 1975. |
| [9] | 刘增文, 王占学, 黄红超, 等. 变循环发动机性能数值模拟[J].航空动力学报, 2010, 25(6): 1310–1315. LIU Z W, WANG Z X, HUANG H C, et al. Numerical simulation on performance of variable cycle engines[J].Journal of Aerospace Power, 2010, 25(6): 1310–1315.(in Chinese) |
| [10] | 苟学中, 周文祥, 黄金泉. 变循环发动机部件级建模技术[J].航空动力学报, 2013, 28(1): 104–111. GOU X Z, ZHOU W X, HUANG J Q. Component-level modeling technology for variable cycle engine[J].Journal of Aerospace Power, 2013, 28(1): 104–111.(in Chinese) |
| [11] | 王元, 李秋红, 黄向华. 变循环发动机建模技术研究[J].航空动力学报, 2013, 28(4): 954–960. WANG Y, LI Q H, HUANG X H. Research of variable cycle engine modeling techniques[J].Journal of Aerospace Power, 2013, 28(4): 954–960.(in Chinese) |
| [12] | 苏三买, 廉小纯. 遗传算法在航空发动机非线性数学模型中的应用[J].推进技术, 2004, 25(3): 237–240. SU S M, LIAN X C. Application of genetic algorithm in aero-engine nonlinear mathematical models[J].Journal of Propulsion Technology, 2004, 25(3): 237–240.(in Chinese) |
| [13] | 苏三买, 陈永琴. 基于混合遗传算法的航空发动机数学模型解法[J].推进技术, 2007, 28(6): 661–664. SU S M, CHEN Y Q. Hybrid genetic algorithm in solving aero-engine nonlinear mathematical model[J].Journal of Propulsion Technology, 2007, 28(6): 661–664.(in Chinese) |
| [14] | 杨伟, 冯雷星, 彭靖波, 等. 求解航空发动机数学模型的混合智能方法[J].推进技术, 2008, 29(5): 614–616. YANG W, FENG L X, PENG J B, et al. An intelligent algorithm for solution of nonlinear mathematical model for aeroengine[J].Journal of Propulsion Technology, 2008, 29(5): 614–616.(in Chinese) |
| [15] | 骆广琦, 刘波, 宋頔源. 基于混合粒子群算法的航空发动机数学模型解法[J].燃气涡轮试验与研究, 2011, 24(2): 5–8. LUO G Q, LIU B, SONG D Y. Hybrid particle swarm optimization in solving aero-engine nonlinear mathematical model[J].Gas Turbine Experiment and Research, 2011, 24(2): 5–8.(in Chinese) |
| [16] | 尹大伟. 航空发动机模型求解算法及性能寻优控制中的参数估计研究[D]. 长沙: 国防科技大学, 2011. YIN D W. Algorithms for solving aero-engine nonlinear mathematical model and parameter estimation in performance-seeking control[D]. Changsha: National University of Defense Technology, 2011(in Chinese). |
| [17] | 白洋, 段黎明, 柳林, 等. 基于改进的混合粒子群算法的变循环发动机模型求解[J].推进技术, 2014, 35(12): 1694–1700. BAI Y, DUAN L M, LIU L, et al. Solving variable cycle engine model based on improved hybrid particle swarm optimization[J].Journal of Propulsion Technology, 2014, 35(12): 1694–1700.(in Chinese) |
| [18] | KURZKE J. GasTurb 12 user's manual:Design and off-design performance of gas turbines[M].Friedrichshafen: MTU Company, 2012: 79-81. |
