EIFS一般通过断口数据反推得到,它不仅与材料特性、加工工艺质量有关,还与细节形式和断口裂纹形态有关。紧固孔是飞机结构中数量最多的细节,其疲劳强度直接影响着飞机的服役寿命。针对紧固孔细节,Fawaz[12]研究了飞机蒙皮搭接和对接2种情况下紧固孔的EIFS分布,Wang[13]探究了多种因素对紧固孔EIFS的影响,证明EIFS是初始表面质量的函数。文献[14]给出各种类型紧固孔的耐久性试验数据并确定了EIFS分布。文献[11-13]均把紧固孔细节的当量初始裂纹形态假设为孔边角裂纹或孔壁半椭圆形裂纹,定义孔壁到裂纹前缘的径向最远距离为裂纹尺寸。若裂纹在孔壁或孔角起裂,采用这种方法是合理的。但是在实际结构中,为了提高细节的抗疲劳性能,方便部件装配,孔边往往要进行倒角处理。文献[14]试验表明,此类细节在疲劳载荷作用下会出现倒角裂纹,即裂纹在倒角与试件表面交点处萌生的情况。结构形式及尺寸的变化(如梁缘条及蒙皮厚度渐变),会形成下陷含孔细节,在拉、弯复合载荷作用下,更容易在倒角处起裂。在这种情况下,若假定初始裂纹为孔壁裂纹或孔角裂纹,以孔壁到裂纹前缘的最远距离作为裂纹长度,会造成如下问题:
1) 由于裂纹在倒角和试件表面交点处萌生,沿试件表面及倒角表面扩展。若以孔壁为裂纹起点,裂纹长度必然大于倒角尺寸,造成萌生寿命过短,与实际情况不符,过于保守。
2) 对于含孔细节,常用的修理方式是扩孔。如果按裂纹前缘到孔壁的距离定义裂纹尺寸,扩孔量会偏大,这会造成修理后剩余寿命降低。
3) 采用反推法确定EIFS时,需要建立裂纹长度随寿命的变化规律,如果裂纹尺寸定义不合理,裂纹扩展规律可能难以描述,从而造成EIFS估计及经济寿命预测结果不准确。
Molent和Yang等指出EIFS与裂纹萌生位置有关[8, 15]。然而对于萌生于孔边倒角的裂纹,尚未建立合理的EIFS确定方法。为此,本文进行孔边倒角的含孔下陷细节试件耐久性试验,研究裂纹萌生和扩展过程,基于断口分析结果,计算分析倒角对裂纹前缘应力强度因子的影响,确定裂纹特征尺寸,并建立孔边倒角裂纹EIFS确定方法。
1 耐久性试验 1.1 试件 试件材料为国产7B04-T74铝合金板材,材料力学性能如表 1所示,取样方向为L-S向。试件的2个孔位于下陷区,模拟某型飞机某关键结构的细节形式。试件的几何形状如图 1所示,孔边倒角尺寸为0.3mm。
表 1 7B04-T74铝合金力学性能 Table 1 Mechanical properties of 7B04-T74 aluminum alloy
| 参数 | 弹性模量 E/GPa | 泊松比 ν | 屈服强度 σs/MPa | 抗拉强度 σb/MPa |
| 数值 | 70 | 0.33 | 450 | 518 |
表选项
 |
| 图 1 试件几何形状 Fig. 1 Geometry of specimen |
| 图选项 |
1.2 载荷谱 基于某型飞机实测过载谱,通过适当调整,形成了可以在断口上留下标识的耐久性载荷谱,一个基本周期代表 1057.998fh(fh为飞行小时)。经试验验证,调整后谱的损伤与原谱损伤相当。采用耐久性谱,进行了2种应力水平下的耐久性试验,单位过载的净截面应力水平分别取为33.5MPa(应力水平1)、31.5MPa(应力水平2)。
1.3 试验结果 试验在Instron8801-100kN电液伺服疲劳试验机上进行。试件直接夹持在试验机夹头上,在室温大气环境下沿轴向加载,试验频率为6Hz。2种应力水平下有效试件数分别为7件和6件。
试件典型断口如图 2所示,断口上留下了较清晰的标识线。
 |
| 图 2 试件典型断口 Fig. 2 Typical fracture surfaces of specimen |
| 图选项 |
1.4 裂纹形态分析 如图 2所示,裂纹均在倒角处萌生,裂纹萌生位置为倒角和试件表面的交点,用A点表示。在裂纹相对较小时,裂纹前缘近似为以A为圆心的圆弧形,沿表面和厚度方向的尺寸基本相同。随着裂纹扩展,裂纹形态逐渐发展为1/4椭圆裂纹,沿孔径方向的尺寸明显大于沿试件厚度方向的尺寸。
2 裂纹特征尺寸的定义 为计算孔边倒角裂纹形态的EIFS,首先应该定义合理的裂纹特征尺寸。裂纹特征尺寸应反映裂纹几何,通常以裂纹前缘到基准线(点)的最长距离作为裂纹特征尺寸。在确定裂纹特征尺寸时,不仅要考虑裂纹萌生位置和前缘形状,还要考虑拟采取的维修方式。
孔角或孔壁萌生的裂纹常表现为孔壁半椭圆形裂纹或孔角椭圆裂纹,通常采用扩孔方式进行修理,因此以孔壁作为基准线,以孔壁到裂纹前缘的最远距离作为裂纹特征尺寸。但是对于倒角处萌生的裂纹,如引言所述,若采用孔壁作为基准线会造成耐久性分析结果偏离实际情况。因此,本节基于1.4节的裂纹形态分析结果,从裂纹前缘的应力强度因子分布及修理时能否去除裂纹前缘塑性区等角度探讨倒角处萌生裂纹的特征尺寸定义方法。
2.1 倒角对裂纹前缘应力强度因子的影响 紧固孔的EIFS常规计算方法通常忽略倒角的影响,将其假设为孔角椭圆裂纹,该裂纹前缘到孔壁和试件表面的距离与倒角裂纹相同。本节基于断口判读得到的裂纹形态和几何尺寸,将图 1所示试件作为分析对象,采用有限元方法计算倒角裂纹与假想的孔角椭圆裂纹2种裂纹形态的裂纹前缘应力强度因子分布,对比分析倒角对裂纹前缘应力强度因子KI的影响。
裂纹形态如图 3所示,针对存在倒角的情况,模拟倒角圆弧裂纹。对无倒角情况,模拟孔角椭圆裂纹,椭圆长轴为孔壁到倒角裂纹前缘的最大长度,即倒角裂纹径向尺寸与倒角尺寸之和,短轴为倒角裂纹沿厚度方向的尺寸。
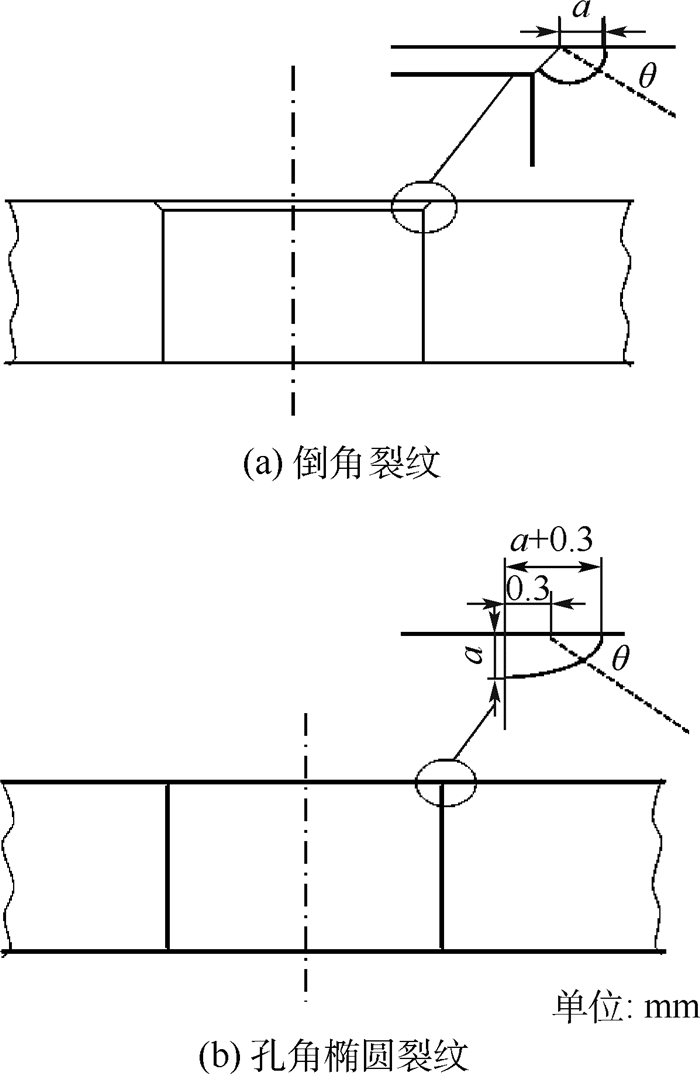 |
| 图 3 有无倒角下的2种裂纹形态 Fig. 3 Shape of two types of cracks initiated at holes with and without chamfering |
| 图选项 |
采用ABAQUS有限元软件提供的相互作用积分法进行应力强度因子的求解,由于试件的对称性,采用1/2有限元模型, 如图 4所示。在试验条件下,试验机夹头相对试件刚度无穷大,试件只能沿轴向移动。因此在试件夹持端模拟夹持边界条件,将试件端部刚化,只保留试件沿加载方向的自由度[16]。
 |
| 图 4 几何模型 Fig. 4 Geometry model |
| 图选项 |
整体的网格划分如图 5所示。裂纹前缘区域采用二次楔形单元(C3D15),如图 6区域1所示。裂纹前缘区域以外的其他区域采用二次六面体单元(C3D20),如图 6区域2所示。本文中奇异单元长度为0.05mm,角度为18°,积分路径数目为5,计算表明,当积分路径数目大于2(即积分区域直径大于0.08mm)时,沿不同积分路径的应力强度因子的计算结果相对误差小于1%。
 |
| 图 5 总体网格 Fig. 5 Mesh of whole model |
| 图选项 |
 |
| 图 6 裂纹前缘附近网格 Fig. 6 Mesh near crack tip |
| 图选项 |
远端拉伸应力取100MPa,不同裂纹尺寸a下,倒角裂纹和孔角椭圆裂纹(见图 3)的应力强度因子KⅠ如图 7所示。为方便比较,对于倒角裂纹和孔角椭圆裂纹,选取相同坐标系,坐标原点为倒角与试件表面的交点A(见图 2),横坐标为裂纹前缘和A点的连线与试件上表面的夹角θ,如图 3所示。考虑到2种裂纹形态下裂纹长度的定义不同,故未对应力强度因子进行无量纲化,纵坐标直接取应力强度因子值。对比结果如图 7所示,可以看出:
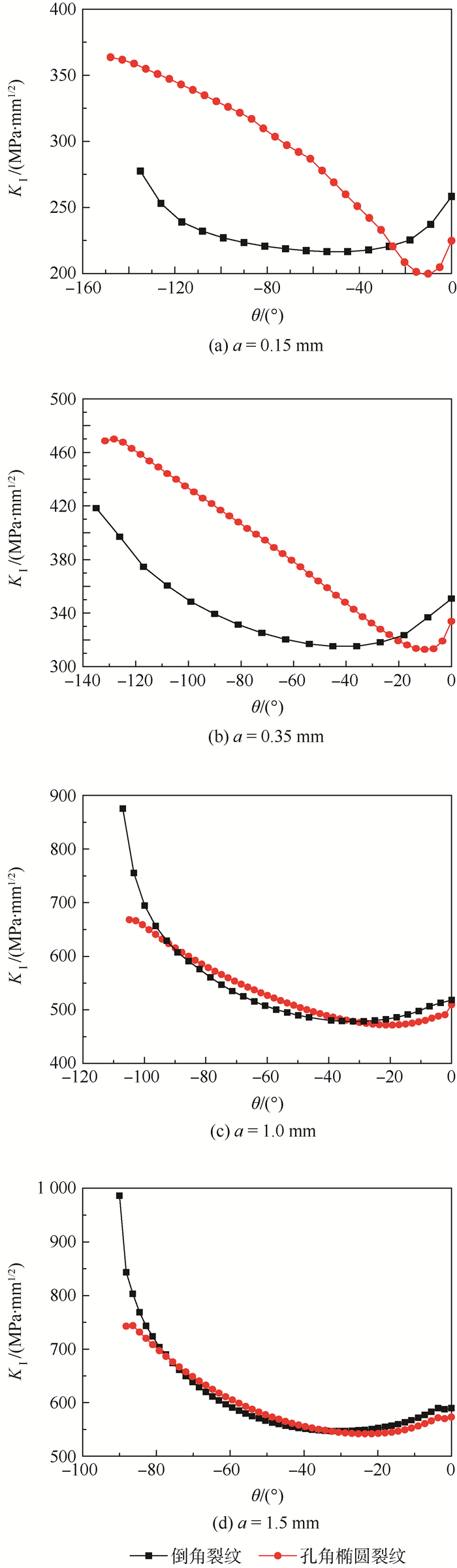 |
| 图 7 2种裂纹形态下应力强度因子的对比 Fig. 7 Comparison of stress intensity factors of two types of cracks |
| 图选项 |
1) 当裂纹尺寸较短(a < 1.5mm)时,2种裂纹形态的应力强度因子分布规律和取值均存在较大的差别。在孔壁附近,孔角椭圆裂纹的应力强度因子值明显高于倒角裂纹的应力强度因子值,最大相差31%;在试件表面附近,倒角裂纹的应力强度因子值略大于孔角椭圆裂纹的应力强度因子值,最大相差13.2%。显然不能将倒角裂纹等效为孔角椭圆裂纹。
2) 当裂纹较长时(a=1.5mm),2种裂纹形态下应力强度因子的分布比较一致,可以将倒角裂纹等效为孔角椭圆裂纹。
2.2 裂纹前缘塑性区尺寸 实际材料不是理想线弹性的,裂纹前缘存在塑性区,在进行结构修理时,必须去除裂纹及裂纹前缘塑性区。从2.1节的应力强度因子计算结果可以看出,若将倒角裂纹等效为孔角椭圆裂纹,在最为关注的试件表面方向应力强度因子计算值小于实际裂纹应力强度因子计算值。由此估计得到的裂纹前缘前缘塑性区尺寸必然小于实际塑性区尺寸,造成偏危险的结果。因此进行塑性区尺寸估计时,应依据实际裂纹形态。
对于倒角裂纹,修理方式有2种。第1种是直接通过扩孔将裂纹及前缘塑性区尺寸去除,然后倒角,如图 8所示(点划线为塑性区范围,虚线为修理方法示意图),此时需要关注尺寸r1。这种修理方式下扩孔量较大,导致剩余强度及剩余寿命低,甚至存在难以实施的可能性。第2种修理方式是先扩孔后倒角,通过扩孔和倒角的综合处理将裂纹及裂纹前缘塑性区去除,如图 9所示。此时,关注的尺寸为r2。显然此种修理方式所需要的扩孔量小于图 8中的做法。若采用此种修理方式,则需计算裂纹前缘塑性区尺寸和范围。塑性区尺寸和范围一般依据裂纹的一个或多个特征尺寸给出,裂纹特征尺寸的选取应参考裂纹前缘塑性区形状。下面进行倒角裂纹的塑性区形状估计。
 |
| 图 8 修理方式1 Fig. 8 Repair scheme 1 |
| 图选项 |
 |
| 图 9 修理方式2 Fig. 9 Repair scheme 2 |
| 图选项 |
对于Ⅰ型裂纹问题,根据裂纹尖端塑性区的二级估计[17],塑性区尺寸可通过式(1)计算:
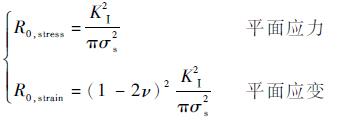 | (1) |
式中:σs为屈服强度,本次试件材料的实测屈服强度为450MPa。
对于三维裂纹,裂纹前缘不同位置的应力状态不同,试件表面(θ=0°)、倒角表面(θ=-135°)以及孔壁均可近似为平面应力状态,除此之外的区域处于复杂应力状态。参考文献[17],裂纹前缘塑性区尺寸可按式(2)计算:
 | (2) |
式中:R0, stress和R0, strain由式(1)计算。
在孔壁附近,由于几何形状复杂,通过该种方法计算的塑性区尺寸有一定误差,但在试件表面附近较为准确。进行倒角时,主要关注试件表面附近的塑性区形态,因此使用该计算方法是可行的。以远端拉应力σ=100MPa为例,在极坐标下绘制裂纹前缘塑性区形状如图 10所示。裂纹前缘的塑性区形状如图 10所示。计算表明,塑性区前缘任一点的切线斜率小于等于1,因此修理时只需在图中点划线位置所示进行倒角,即可完全去除塑性区。此时需要关注的是试件表面的塑性区尺寸。
 |
| 图 10 塑性区形状 Fig. 10 Plastic zone shape |
| 图选项 |
2.3 裂纹特征尺寸确定 对于倒角裂纹,采用图 9所示的经济修理方式时,需关注试件表面的塑性区尺寸。同时在进行断口判读时,沿试件表面方向(孔径向)的裂纹尺寸更容易读取。综上所述,在进行EIFS分析时,应将初始裂纹假设为倒角裂纹,以萌生点到裂纹前缘的径向距离为裂纹特征尺寸,如图 3(a)所示。
3 EIFS分析 在倒角裂纹尺寸定义下,计算得到EIFS是否能真实反映结构的IFQ有待进一步验证。本节在倒角裂纹尺寸定义基础上,计算得到不同应力水平下的EIFS分布,并进行统计对比,检验其是否与应力水平无关,从而间接说明本文定义方式的合理性。并在此基础上,计算得到含孔下陷细节的EIFS分布。
根据文献[18],EIFS分布的确定一般有2种方法,一种是TTCI反推法,首先计算每个试件达到指定裂纹尺寸的时间(Time to Crack Initiation, TTCI),假设TTCI服从某一特定分布,通过TTCI分布反推得到EIFS分布。另一种是EIFS拟合法,即直接反推得到EIFS样本,选定合适的分布类型,通过统计处理得到分布参数。本文采用后者。
3.1 EIFS控制曲线的建立 首先,通过对试件进行断口判读得到(a, t)数据,绘制a-t曲线,如图 11所示。可以看出a-t曲线在对数坐标下呈分段线性,裂纹较短和较长时a-t曲线的斜率不同。考虑到耐久性分析的范围,取1.2mm以下[18]的a-t数据进行分析,如图 12所示,在对数坐标系中相对小裂纹的a-t曲线近似为一条直线。对于相对小裂纹,通常采用式(3)描述其裂纹扩展规律:
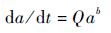 | (3) |
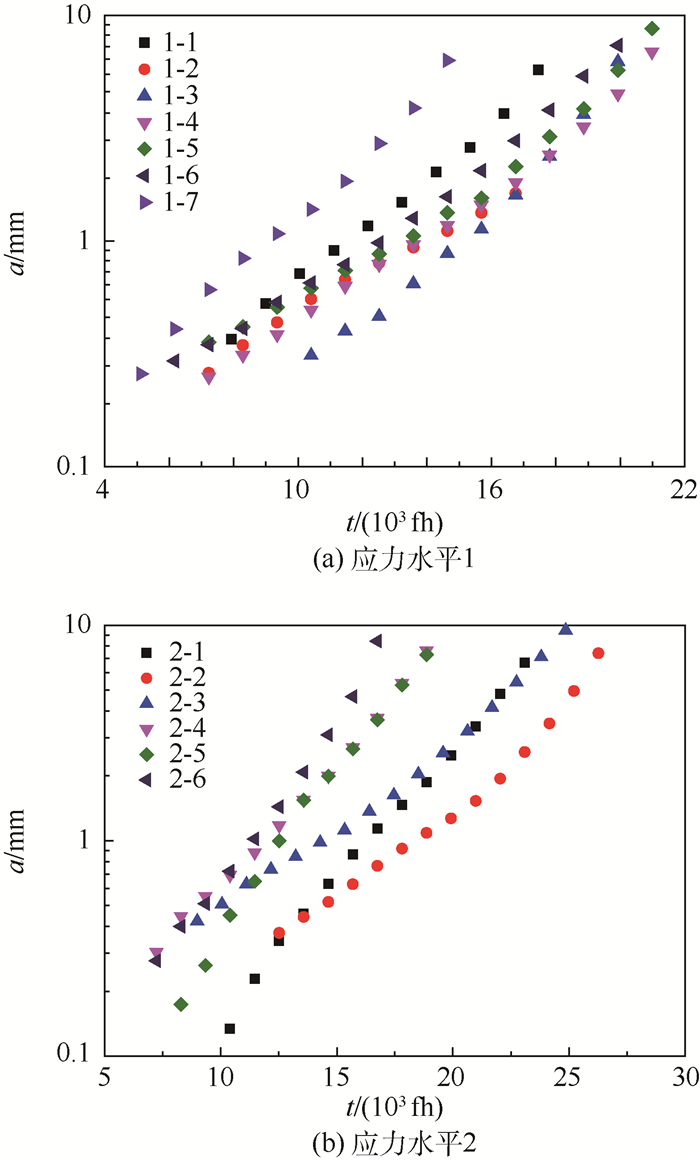 |
| 图 11 裂纹扩展数据 Fig. 11 Crack growth data |
| 图选项 |
 |
| 图 12 相对小裂纹a-t数据 Fig. 12 a-t data for relatively small crack |
| 图选项 |
式中:Q为裂纹扩展速度参数;b为裂纹扩展方程指数。
式(3)是基于描述裂纹扩展过程的Paris公式形式,将三维裂纹应力强度因子计算公式作级数展开,取低阶项得到的近似表达式[19]。当裂纹长度较小时,该式具有很好的适用性。由于该细节应力集中区的应力状态复杂,该式的适用性需要通过建立试件表面裂纹前缘应力强度因子与a的变化关系曲线来验证。因此,基于试验断口判读的裂纹形态和尺寸,进行了相对小裂纹情况下裂纹特征尺寸对应的试件表面裂纹前缘应力强度因子随特征尺寸变化的有限元模拟。对应力强度因子进行无量纲化,令

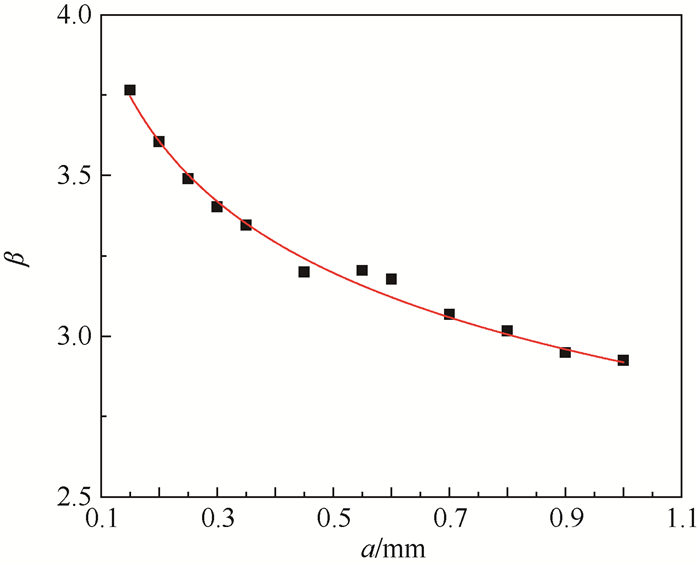 |
| 图 13 无量纲化应力强度因子随裂纹尺寸变化曲线 Fig. 13 Changing curve of non-dimensional stress intensity factor with crack size |
| 图选项 |
对式(3)两边取对数,得到ln(da/dt)= ln Q+bln a。根据文献[18]中的方法,计算得到2种应力水平下,b分别为1.066和0.949,因此可近似取b=1。
根据文献[18],每个试件的裂纹扩展速度参数Qik由该试件的断口数据决定。采用最小二乘法,由a-t数据,直接拟合得到Q值,第i种应力水平,第k个试件的裂纹扩展方程参数Qik由该试件的mik个断口数据(aikj, tikj)(j=1, 2, …, mik)数据通过式(4)计算:
 | (4) |
指定参考裂纹尺寸ar下EIFS控制方程如式(5)所示。取ar=0.5mm计算得到试件的EIFS如图 14所示。
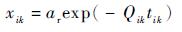 | (5) |
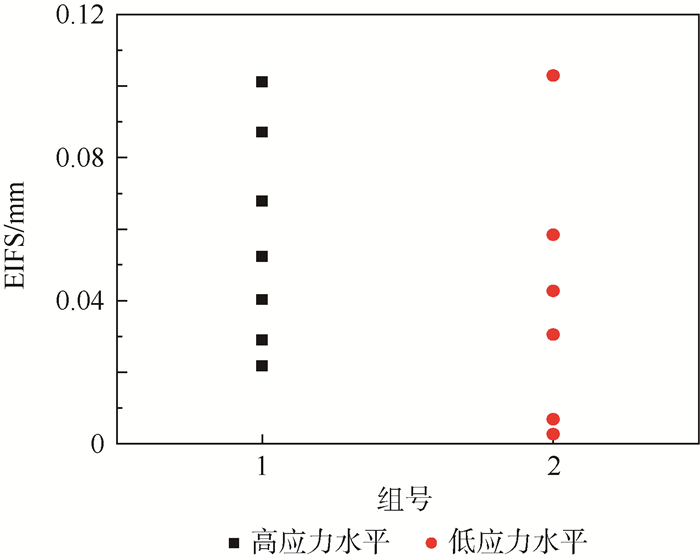 |
| 图 14 EIFS值 Fig. 14 EIFS value |
| 图选项 |
3.2 2种应力水平下的EIFS的对比 假定EIFS服从对数正态相容分布,引入随机变量Z=ln ln(ar/X)=ln(QT),其中X代表EIFS总体,T为裂纹萌生时间总体,Z满足正态分布。EIFS的分布函数如式(6)所示。分布参数可通过式(7)进行估计。在ar=0.5mm时,得到2种应力水平下的Z的分布概率函数,分布参数如表 2所示。
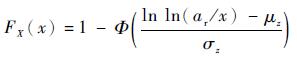 | (6) |
表 2 2种应力水平下Z分布参数估计 Table 2 Z distribution parameter estimation for two stress levels
| 应力水平 | 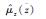 |  |
| 应力水平1 | 0.806 | 0.250 |
| 应力水平2 | 1.043 | 0.443 |
表选项
式中:x为EIFS值。
 | (7) |
1) 方差齐性检验
采用F检验法,取显著度水平α=0.05,对2种应力水平下Z1(应力水平1),Z2(应力水平2)进行方差齐性检验,根据参考文献[20],F值如式(8)所示。因此,可认为Z1,Z2具有方差齐性,其综合标准差如式(9)所示。
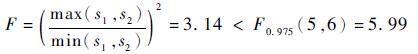 | (8) |
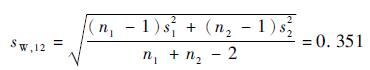 | (9) |
2) 差异性检验
采用t检验法,取显著度水平为α=0.05,根据参考文献[20],t值如式(10)所示,因此可认为在这Z1,Z2中值寿命没有显著差异。因此2个样本来自同一母体,即EIFS与应力水平无关。
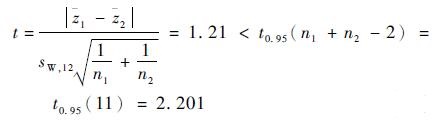 | (10) |
3.3 通用EIFS估计 在2种应力水平下,通过式(5)得到指定ar下EIFS分布的一组大样本,其母体的分布参数可通过式(7)进行估计。对
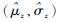
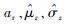
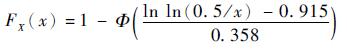 | (11) |
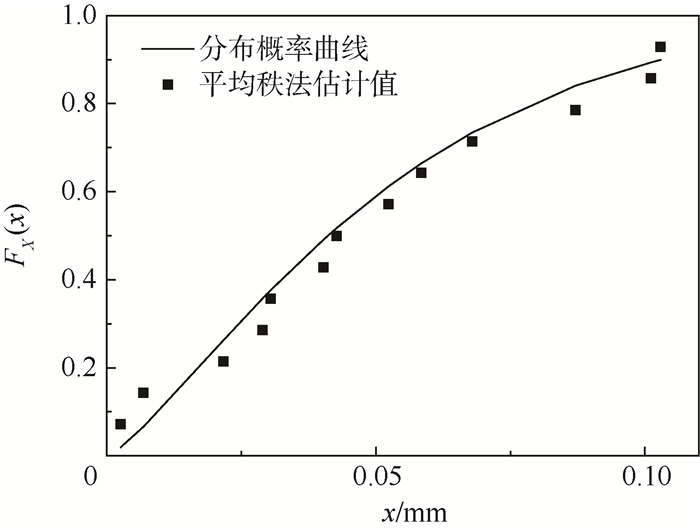 |
| 图 15 分布概率函数曲线 Fig. 15 Probability distribution function curve |
| 图选项 |
4 讨论 1) 在实验室条件下,试验机夹持边界条件可等效为远场均布拉伸载荷和试件端部除轴向位移之外的所有约束的共同作用。文献[16]表明对于不对称裂纹,在裂纹扩展过程中,试件刚度发生变化,导致远场弯矩发生变化,因此在裂纹扩展过程中,Q有一定变化。由于含孔下陷试件偏弯现象比较明显,这种影响更为显著。3.1节为得到EIFS控制曲线,进行了倒角裂纹应力强度因子的有限元计算。计算结果表明应力强度因子与裂纹尺寸的关系可用幂函数表示。这说明弯矩的变化对裂纹扩展方程的影响较小,可忽略。因此,选取相对小裂纹扩展方程来描述裂纹扩展规律是合理的。
2) 假设检验表明在本文定义的裂纹特征尺寸下,2种应力水平下的EIFS分布无显著差异,说明本文计算得到的EIFS与应力水平无关,可以作为试件初始缺陷的表征。但是,一方面EIFS是一个当量化的数学概念,并非实际的材料初始缺陷,另一方面,很难通过断口判读直接得到0时刻的裂纹长度[2],因此并不能直接通过试验结果验证本文中计算得到的EIFS分布的合理性。
3) 由图 15可看出,该种裂纹形态的EIFS值在0.1mm以内,中值约为0.05mm。若使用孔角椭圆裂纹来定义初始裂纹计算EIFS,中值约为0.11mm,部分EIFS值甚至达到0.17mm。根据文献[8],铝合金含孔细节不同加工工艺下的EIFS均在0.1mm以下,因此使用本文定义的初始裂纹和特征尺寸计算的EIFS更为合理。
5 结论 本文针对孔边倒角处萌生裂纹的含孔下陷细节,选取合适的裂纹特征尺寸。并基于该尺寸,由耐久性试验断口数据反推得到EIFS的分布。有以下结论:
1) 在裂纹相对较小(1.5mm以下)情况下,孔角椭圆裂纹和倒角裂纹的应力强度因子分布存在很大差异,进行塑性区估计时应采用真实的裂纹形态。
2) 对于倒角处萌生的裂纹,应将裂纹特征尺寸定义为倒角与试件表面的交点到裂纹前缘沿孔径向的距离。
3) 采用反推法得到的倒角裂纹EIFS分布与应力水平无关。说明该特征尺寸下的EIFS可以合理表征结构的原始疲劳质量。
参考文献
| [1] | TONG Y C.Literature review on aircraft structural risk and reliability analysis:DSTO-TR-1110[R].Melboure:DSTO Aeronautical and Maritime Research Labratory, 2001. |
| [2] | RUDD J L, GRAY T D. Quantification of fastener-hole quality[J].Journal of Aircraft, 1978, 15(3): 143–147.DOI:10.2514/3.58332 |
| [3] | RUDD J L.Applications of the equivalent initial quality method:AFFDL-TM-76-83-FBE[R].Dayton:Wright-Patterson AFB, 1977. |
| [4] | MANNING S D, YANG J N, SHINOZUKA M.USAF durability design handbook:Guidelines for the analysis and design of durable aircraft structures:AFFDL-TR84-3027[R].Dayton:Wright-Patterson AFB, 1984. |
| [5] | YANG J N. Statistical estimation of economic life for aircraft structures[J].Journal of Aircraft, 1980, 17(7): 528–535.DOI:10.2514/3.57935 |
| [6] | BARTER S A, MOLENT L. Fatigue cracking from a corrosion pit in an aircraft bulkhead[J].Engineering Failure Analysis, 2014, 39(4): 155–163. |
| [7] | MOLENT L. A review of equivalent pre-crack sizes in aluminium alloy 7050-T7451[J].Fatigue & Fracture of Engineering Materials & Structures, 2014, 37(10): 1055–1074. |
| [8] | MOLENT L, SUN Q, GREEEN A J. Characterisation of equivalent initial flaw sizes in 7050 aluminium alloy[J].Fatigue & Fracture of Engineering Materials & Structures, 2006, 29(11): 916–937. |
| [9] | MATTRAND C, BOURINET J M, THéRET D.Analysis of fatigue crack growth under random load sequences derived from military in-flight load data[C]//ICAF 2011 Structural Integrity:Inuence of Eciency and Green Imper-atives.Berlin:Springer-Verlag, 2011:399-413. |
| [10] | MATTRAND C, BOURINET J M. Random load sequences and stochastic crack growth based on measured load data[J].Engineering Fracture Mechanics, 2011, 78(17): 3030–3048.DOI:10.1016/j.engfracmech.2011.08.022 |
| [11] | XIANG Y, LIU Y. EIFS-based crack growth fatigue life prediction of pitting-corroded test specimens[J].Engineering Fracture Mechanics, 2010, 77(8): 1314–1324.DOI:10.1016/j.engfracmech.2010.03.018 |
| [12] | FAWAZ S A. Equivalent initial flaw size testing and analysis of transport aircraft skin splices[J].Fatigue & Fracture of Engineering Materials & Structures, 2003, 26(3): 279–290. |
| [13] | WANG D Y.An investigation of initial fatigue quality:STPZ8860S[R].West Conshohocken:ASTM Special Technical Publication, 1982. |
| [14] | 航空航天部AFFD系统办公室. 美国空军耐久性手册背景材料: 第Ⅷ卷[M]西安: 航空航天部AFFD系统办公室, 1989. AFFD System Engineering Office of the Department of Aeronautics and Astronautics. The background information of USAF durability design handbook:Vol.Ⅷ[M].Xi'an:AFFD System Engineering Office of the Department of Aeronautics and Astronautics, 1989(in Chinese). |
| [15] | YANG J, MANNING S, RUDD J, et al.Effect of specimen size and notch geometry on equivalent initial flaw size distribution[C]//AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit.Reston:AIAA, 1996:385-397. |
| [16] | 曹淑森, 贺小帆, 杨博霄, 等. 夹持边界条件下表面裂纹应力强度因子求解[J].北京航空航天大学学报, 2014, 40(11): 1637–1642. CAO S S, HE X F, YANG B X, et al. Solution of stress intensity factor of surface cracked geometry with clamped ends[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(11): 1637–1642.(in Chinese) |
| [17] | 张行. 断裂力学[M].北京: 中国宇航出版社, 1990: 72-169. ZHANG X. Fracture mechanics[M].Beijing: China Aerospace Press, 1990: 72-169.(in Chinese) |
| [18] | 刘文珽. 概率断裂力学与概率损伤容限/耐久性[M].北京: 北京航空航天大学出版社, 1999: 144-181. LIU W T. Probabilistic fracture mechanics and probability damage tolerance/durability[M].Beijing: Beihang University Press, 1999: 144-181.(in Chinese) |
| [19] | PROVAN J W. Probabilistic fracture mechanics and reliability[M].Leiden: Martinus Nijhoff Publishers, 1987: 70-72. |
| [20] | 高镇同. 疲劳应用统计学[M].北京: 国防工业出版社, 1986: 277-295. GAO Z T. Fatigue application statistics[M].Beijing: National Defence of Industry Press, 1986: 277-295.(in Chinese) |
