然而,WENO格式在连续解一阶极值点处精度会降低(例如五阶WENO格式在一阶极值点处会降为三阶)[5]。为了提高WENO格式在极值点处的精度,Borges等[6]通过构造全局高阶光滑因子的方式,提出五阶WENO-Z格式,该格式在间断区域附近比基于映射权函数的WENO-M格式的耗散性小。Yamaleev和Carpenter[7]在改进WENO-Z格式全局光滑因子的基础上,推导给出三阶能量稳定WENO格式。Wu等[8-9]根据Hu等[10]的思想,通过线性组合局部模板和全局模板光滑因子的方式推导给出改进的三阶WENO-Z格式。Acker等[11]在Borges等[6]工作的基础上,通过增大非光滑模板所对应的非线性权重的方式,推导给出五阶WENO-Z+格式,该格式具有比五阶WENO-Z格式更低的耗散特性。
从文献[8-11]可以发现,当前对WENO-Z格式的改进方法主要分为2种:①通过合理构造全局光滑因子的方式;②通过增大非光滑模板所对应的非线性权重的方式。
为了进一步探讨全局光滑因子对WENO-Z格式计算精度的影响规律,需要寻求新的思路改进WENO-Z格式。本文根据文献[7-9]的研究,在三阶WENO-Z格式基础上,通过构造不同形式的全局光滑因子得到WENO-Z3N1、WENO-Z3N2、WENO-Z3N3格式。在经典算例验证与理论推导的基础上,通过探讨各格式理论精度与实际计算精度之间的关系发现:连续解非极值点处的理论精度对改进的三阶WENO-Z格式计算精度起决定性的作用。
1 控制方程 含激波流场采用可压缩欧拉方程进行描述,其具体形式如下:
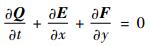 | (1) |
式中:
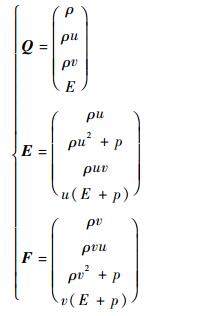 | (2) |
 | (3) |
式中:Q、E、F分别为守恒通量、x方向数值通量、y方向数值通量;ρ为密度;u、v分别为x、y方向上的速度分量;p为流体压力;E为单位体积流体的总能量;e为比内能;γ为气体的绝热指数,本文取1.4。
2 数值方法 2.1 三阶WENO格式 三阶WENO格式(WENO-JS3)的数值离散过程如下[2]:单元面中心
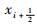
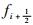
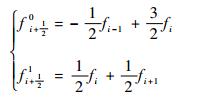 | (4) |
式中:fi为节点i处的数值通量。
利用式(4)2个子模板低阶数值通量的凸组合计算数值通量
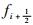
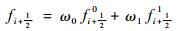 | (5) |
式中:ωk为非线性权因子,对于含激波间断流场则需要根据式(6)求得
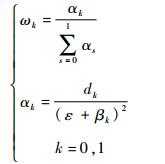 | (6) |
其中:d0=1/3;d1=2/3;ε=1.0×10-6;光滑因子βk(k=0, 1)的表达式为
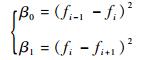 | (7) |
在光滑流场区域,该格式满足设计精度的充分条件为[7]
 | (8) |
式中:O(h2)表示该数值与h2同量级,h为均匀网格步长。
2.2 三阶WENO-Z格式 三阶WENO-Z格式(WENO-Z3)的具体形式如下[12]:
 | (9) |
 | (10) |
将式(7)代入式(10)可得全局光滑因子τ为
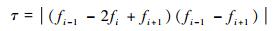 | (11) |
参考式(11)的构造方式,进一步给出以下3种不同组合形式的全局光滑因子:
 | (12) |
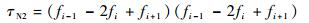 | (13) |
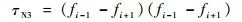 | (14) |
本文将采用τN1、τN2、τN3全局光滑因子的格式分别简记为WENO-Z3N1、WENO-Z3N2、WENO-Z3N3。
2.3 时间项数值离散 采用三阶TVD-RK法[13]对欧拉方程中时间项进行数值离散,格式如下:
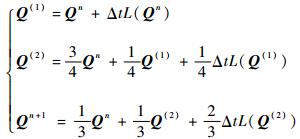 | (15) |
式中:Qn为n时刻的守恒通量;Q(1)、Q(2)为中间变量;Qn+1为n+1时刻的守恒通量;Δt为时间步长;L(·)为运算算子。
3 数值试验 3.1 Sod激波管 该算例初始条件如式(16)所示,网格数为200,计算结束时间为0.18。图 1给出计算结束时刻密度曲线局部放大图。
 |
| 图 1 Sod激波管计算结束后密度曲线局部放大图 Fig. 1 Partial enlarged details of density curves after calculation for Sod shock tube |
| 图选项 |
 | (16) |
式中:x为位置坐标。
3.2 双爆轰波碰撞 该算例初始条件如式(17)所示,网格数为800,计算结束时间为0.038。图 2给出计算结束时刻密度曲线局部放大图。
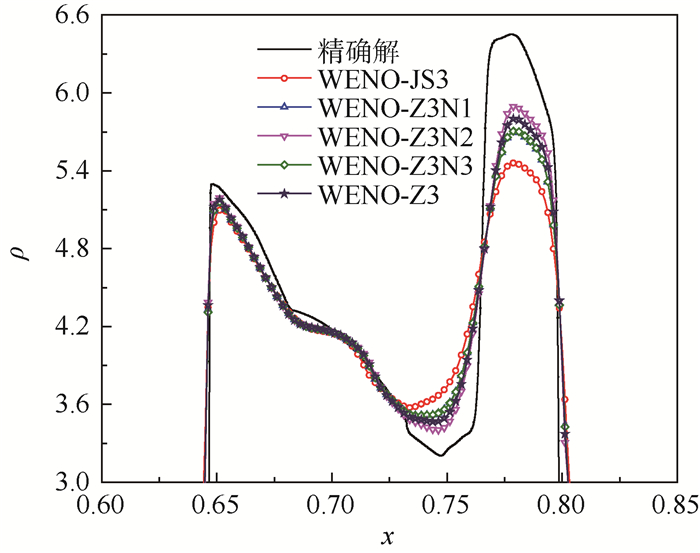 |
| 图 2 双爆轰波碰撞计算结束后密度曲线局部放大图 Fig. 2 Partial enlarged details of density curves after calculation for interacting blast waves |
| 图选项 |
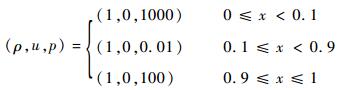 | (17) |
3.3 激波与熵波相互作用 该算例初始条件如式(18)所示,网格数为800,计算结束时间为1.8。图 3给出计算结束时刻密度曲线局部放大图。
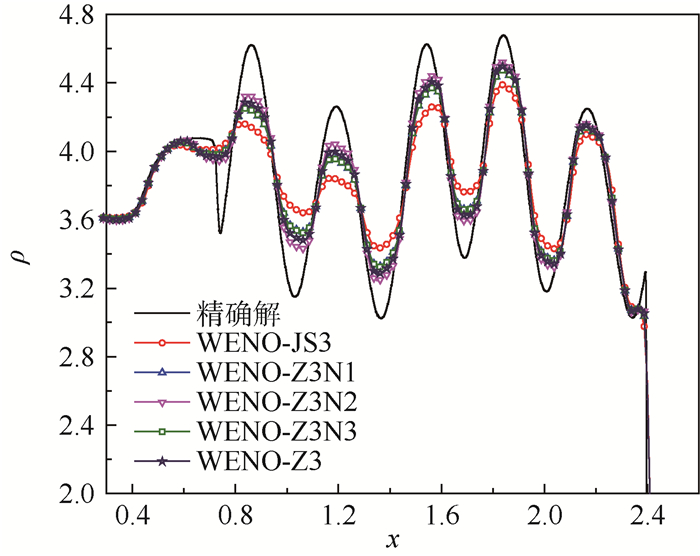 |
| 图 3 激波与熵波相互作用计算结束后密度曲线局部放大图 Fig. 3 Partial enlarged details of density curves after calculation for shock entropy wave interaction |
| 图选项 |
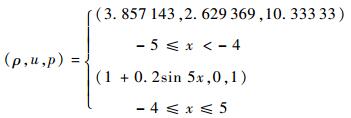 | (18) |
根据图 1~图 3的计算结果,评估各格式的总体计算性能发现:3种改进格式WENO-Z3N2格式计算性能最优,WENO-Z3格式次之,WENO-Z3N1格式与WENO-Z3N3格式计算性能基本相同,WENO-JS3格式计算性能最低。且3种格式的计算性能均优于传统的WENO-JS3格式。然而,通过线性对流方程精度测试发现,3种格式在一阶极值点处均没有达到设计精度。
4 理论精度分析 为了深入探讨不同全局光滑因子对WENO-Z格式计算性能的影响规律,本节主要从3种改进格式在连续解处(非极值点处和极值点处)理论精度的角度进行分析。
4.1 WENO-Z3格式 这里主要对WENO-Z3格式的理论精度进行推导,式(11)在连续解非极值点处可得
 | (19) |
再根据式(9)可得
 | (20) |
式(11)在连续解极值点处可得
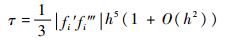 | (21) |
再根据式(9)可得
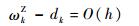 | (22) |
4.2 WENO-Z3N1格式 本节主要对WENO-Z3N1格式的理论精度进行推导,式(12)在连续解非极值点处可得
 | (23) |
再根据式(9)可得
 | (24) |
式(12)在连续解极值点处可得
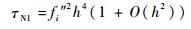 | (25) |
再根据式(9)可得
 | (26) |
4.3 WENO-Z3N2格式 这里主要对WENO-Z3N2格式的理论精度进行推导,式(13)在连续解非极值点处可得
 | (27) |
再根据式(9)可得
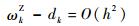 | (28) |
式(13)在连续解极值点处可得
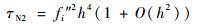 | (29) |
再根据式(9)可得
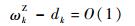 | (30) |
4.4 WENO-Z3N3格式 本节主要对WENO-Z3N3格式的理论精度进行推导,式(14)在连续解非极值点处可得
 | (31) |
再根据式(9)可得
 | (32) |
式(14)在连续解极值点处可得
 | (33) |
再根据式(9)可得
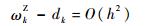 | (34) |
4.5 计算精度与理论精度关系探讨 针对格式WENO-Z3N1和WENO-Z3N3,从连续解非极值点处的理论精度进行评估可知:WENO-Z3N1格式的计算性能应与WENO-Z3N3格式相同。而从连续解极值点处的理论精度进行评估可知:WENO-Z3N3格式的计算性能应优于WENO-Z3N1。而通过第3节算例的计算结果发现,这2个格式几乎给出相同的计算结果。因此可以初步认为:WENO-Z格式在连续解非极值点处的理论精度对实际计算性能起主要作用。
针对格式WENO-Z3N2和WENO-Z3,从连续解非极值点处精度进行评估可得:WENO-Z3N2格式的计算性能应优于WENO-Z3。而从连续解极值点处精度进行评估可得:WENO-Z3格式的计算性能应优于WENO-Z3N2。而通过第3节算例的计算结果发现,WENO-Z3N2格式的实际计算性能优于WENO-Z3格式。进一步说明:连续解非极值点处的理论精度对3种格式的实际计算性能起主要作用。
从各数值格式在连续解非极值点处对式的满足要求程度进行评估可知,WENO-Z3N2格式最优,WENO-Z3格式次之,WENO-Z3N1格式与WENO-Z3N3格式基本相同。这一评估结果与第3节算例的计算结果相吻合。充分说明各格式在连续解非极值点处的理论精度对实际计算性能起决定性的作用。因此本文建议:对于三阶WENO-Z格式的优化,可以通过构造全局光滑因子使得格式在连续解非极值点处满足式(8)的要求。
5 二维算例验证 为了进一步考察3种改进格式对于多维复杂流场的计算性能,选取经典的双马赫反射问题进行数值计算。
强激波的双马赫反射(double Mach reflection)问题是测试数值格式的分辨率以及对间断的捕捉特性的标准算例之一[14-16]。该算例的计算网格数选取为1 920×480,计算时间为0.2。
图 4分别为WENO-JS3、WENO-Z3N1、WENO-Z3N2、WENO-Z3N3、WENO-Z3格式在马赫杆附近区域计算结果,y为计算域的高度。密度图为40条等间距等值线,密度变化范围为1.8~20。从图 4可知,WENO-Z3N1、WENO-Z3N2、WENO-Z3N3、WENO-Z3计算精度明显优于WENO-JS3,均能分辨滑移线引起的涡结构(见图 4(b)~图 4(e))。格式WENO-Z3N1与格式WENO-Z3N3几乎给出相同的计算结果(见图 4(b)、图 4(d))。其中,WENO-Z3N2和WENO-Z3格式相较其他格式能较好地分辨水平滑移线引起的涡结构(见图 4(c)、图 4(e)),且WENO-Z3N2格式给出更精细的涡结构。说明格式WENO-Z3N2在上述格式中计算性能最优。双马赫反射算例的计算结果进一步验证了4.5节的结论。
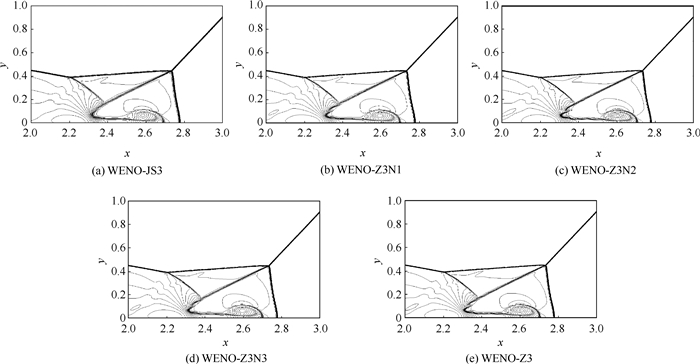 |
| 图 4 双马赫反射马赫杆附近局部放大图 Fig. 4 Density contours of enlarged portion near Mach stems for the double Mach reflection problem |
| 图选项 |
6 结论 本文采用经典算例的计算与理论精度分析相结合的方式探讨了全局光滑因子对WENO-Z格式计算性能的影响规律。通过对计算结果的分析可以得到:
1) WENO-Z3N2格式在连续解非极点处满足设计精度要求,相较其他格式具有更低耗散、更高分辨率的特性。
2) 针对三阶WENO-Z格式,合理构造全局光滑因子使得格式在连续解非极值点处满足设计精度要求是一种较好的改进方法。
参考文献
| [1] | LIU X D, OSHER S, CHAN T. Weighted essentially non-oscillatory schemes[J].Journal of Computational Physics, 1994, 115(1): 200–212.DOI:10.1006/jcph.1994.1187 |
| [2] | JIANG G S, SHU C W. Efficient implementation of weighted ENO schemes[J].Journal of Computational Physics, 1996, 126(1): 202–228.DOI:10.1006/jcph.1996.0130 |
| [3] | SHU C W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws[M].Berlin: Springer, 1998: 325-432. |
| [4] | SHU C W. High order weighted essentially nonoscillatory schemes for convection dominated problems[J].SIAM Review, 2009, 51(1): 82–126.DOI:10.1137/070679065 |
| [5] | HENRICK A K, ASLAM T D, POWERS J M. Mapped weighted essentially non-oscillatory schemes:Achieving optimal order near critical points[J].Journal of Computational Physics, 2005, 207(2): 542–567.DOI:10.1016/j.jcp.2005.01.023 |
| [6] | BORGES R, CARMONA M, COSTA B, et al. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws[J].Journal of Computational Physics, 2008, 227(6): 3191–3211.DOI:10.1016/j.jcp.2007.11.038 |
| [7] | YAMALEEV N K, CARPENTER M H. Third-order energy stable WENO scheme[J].Journal of Computational Physics, 2009, 228(8): 3025–3047.DOI:10.1016/j.jcp.2009.01.011 |
| [8] | WU X, ZHAO Y. A high-resolution hybrid scheme for hyperbolic conservation laws[J].International Journal for Numerical Methods in Fluids, 2015, 78(3): 162–187.DOI:10.1002/FLD.v78.3 |
| [9] | WU X, LIANG J, ZHAO Y. A new smoothness indicator for third-order WENO scheme[J].International Journal for Numerical Methods in Fluids, 2015, 81(7): 451–459. |
| [10] | HU X Y, WANG Q, ADAMS N A. An adaptive central-upwind weighted essentially non-oscillatory scheme[J].Journal of Computational Physics, 2010, 229(23): 8952–8965.DOI:10.1016/j.jcp.2010.08.019 |
| [11] | ACKER F, BORGES R B D R, COSTA B. An improved WENO-Z scheme[J].Journal of Computational Physics, 2016, 313: 726–753.DOI:10.1016/j.jcp.2016.01.038 |
| [12] | DON W S, BORGES R. Accuracy of the weighted essentially non-oscillatory conservative finite difference schemes[J].Journal of Computational Physics, 2013, 250(4): 347–372. |
| [13] | SHU C W, OSHER S. Efficient implementation of essentially non-oscillatory shock-capturing schemes[J].Journal of Computational Physics, 1988, 77(2): 439–471.DOI:10.1016/0021-9991(88)90177-5 |
| [14] | SHI J, ZHANG Y T, SHU C W. Resolution of high order WENO schemes for complicated flow structures[J].Journal of Computational Physics, 2003, 186(2): 690–696.DOI:10.1016/S0021-9991(03)00094-9 |
| [15] | 吴晓帅, 赵玉新. 低耗散中心-WENO混合格式[C]//中国计算力学大会2014暨钱令希计算力学奖颁奖大会论文集. 北京: 中国计算力学大会, 2014: 890-895. WU X S, ZHAO Y X.Low-dissipation hybrid central-WENO scheme[C]//Proceedings of Conference on Computational Mechanics in China 2014 and Qian Lingxi Computational Mechanics Awards Assembly.Beijing:China Computational Mechanics Conference, 2014:890-895(in Chinese). |
| [16] | 王来, 吴颂平. 无自由参数型混合格式[J].北京航空航天大学学报, 2015, 41(2): 318–322. WANG L, WU S P. Hybrid finite difference schemes without parameters[J].Journal of Beijign University of Aeronautics and Astronautics, 2015, 41(2): 318–322.(in Chinese) |
