Roy等[1]通过实验研究发现对旋风机可以提高风机的整体性能并改善内部流动并讨论了对旋风机之后改进的措施。Pundhir和Sharma[2]通过实验的方法研究了转速比和转子间轴向间距对对旋风机气动性能的影响。陈云永等[3]通过实验和数值的方法对不同转速比和轴向间隙条件对压气机性能影响进行了研究。杨小贺和单鹏[4]设计并通过数值计算分析了2种对旋风机设计的流动以及2种设计的失速裕度。高丽敏等[5]通过数值方法研究了转速比对压气机最先失速级的影响。Mistry和Pradeep[6]通过实验研究了对旋风机受来流畸变的影响,比较分析了轮毂处畸变较强和机匣处畸变较强2种情况。王卓奇等[7]通过实验方法验证了对旋风机不同转速分配可以改变失速关键级。Zhang等[8]通过非定常数值计算的方法研究了对旋风机受转-转干涉的影响,发现非定常流动对第2级转子影响较大。王掩刚等[9]通过实验的方法研究了对旋风机的失速,结果发现失速最先发生在第2级且只有一个失速团。Cho等[10]对高效对旋风机的气动设计进行了数值和实验的分析。艾子健等[11]利用速度三角形推导出不同工况下两级叶轮转速匹配的计算公式,提出了不同工况对应不同两级叶轮转速的转速匹配方法。Wang等[12]通过实验研究了改变前后两级转子的载荷分布和旋转速度的比对风机性能的影响。刘波等[13]通过实验和计算研究了对旋风机前后级转子不同转差下的特性以及对流场和性能的影响。
上述文献从气动方面研究了对旋风机的转速变化主要集中在对风机流动和性能影响等方面的定性分析。但是,并未对转速改变后相关流动参数进行定量的阐述。因此本文在此方面进行研究,通过速度三角形分析给出速度变化后流动参数的定量分析,通过数值和实验分析转速改变后风机内部流动改变,对速度三角形的分析进行验证分析确定最优转速比。
1 对旋风机物理模型和数学模型 1.1 物理模型 本文研究的风机的叶轮分别由2个11 kW的电机驱动,前后两级叶片数目分别为11和9。两级叶轮的旋转速度都是3000r/min,旋转方向相反,原型风机设计质量流量为7.57 kg/s,设计全压升为2 000 Pa。风机的基本结构和实验测点如图 1所示,叶片结构如图 2所示。
 |
| 图 1 对旋风机的基本结构及测点分布 Fig. 1 Fundamental structure of counter rotating fan and distribution of measuring points |
| 图选项 |
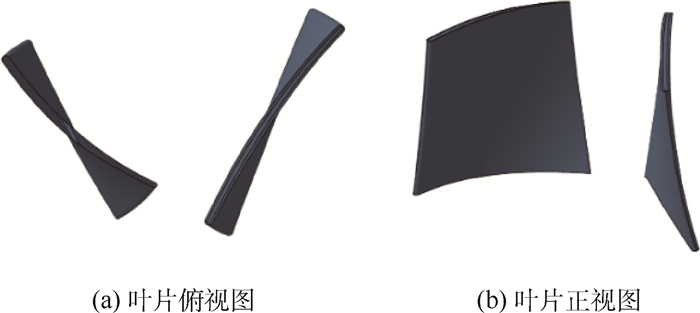 |
| 图 2 对旋风机的叶片几何 Fig. 2 Blade geometry of counter rotating fan |
| 图选项 |
1.2 数值方法 本文采用Numeca软件以理想气体为工质对风机的中气体流动进行计算,气动计算采用雷诺应力湍流模型(RSM)进行计算。
相比于单方程和双方程模型,雷诺应力湍流模型可以用来计算各向异性的复杂三维湍流流场,并准确地反映湍流各向异性的特点,且可以清楚地给出涡的结构[14-15],因此本文采用雷诺应力湍流模型进行计算。由于计算的工质空气的温度未超过500 K且计算过程中最大压力未超过101 325 Pa过多,故采用理想空气模型简化空气的密度变化。
1.3 网格模型 在确定原型几何与湍流模型后,根据湍流模型对网格的要求划分网格。本文的网格采用更容易控制质量和加密的结构化网格(见图 3),对单一通道划分了网格,网格数量为150万,第1层网格的高度为10-5 m,经计算后验证Y+满足湍流模型的要求,经过了网格无关性验证,计算结果表明网格质量满足计算模型需求。
 |
| 图 3 计算网格 Fig. 3 Computational grid |
| 图选项 |
1.4 边界条件 风机的进口总压Pin*为101 325 Pa,进口总温Tin*为273.15 K,基准转速为前后两级均为3 000r/min(记为转速3 000-3 000,下文均使用此种表示方法),之后在保持一级转速不变的情况下,调整另一级转速分别为标准转速的0.6、0.8、1.2和1.4倍(分别对应转速变化-40%、-20%、20%和40%)进行计算。
2 速度三角形分析 改变转速后,直接改变了叶片的流动速度三角形,其变化如图 4所示。
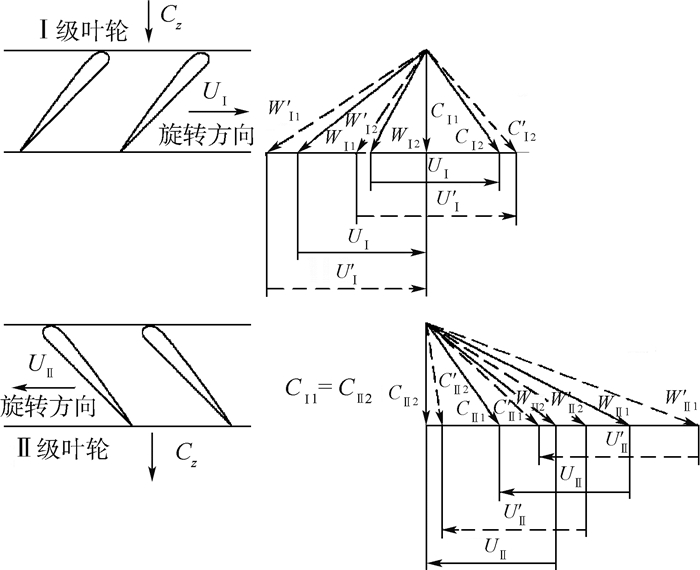 |
| 图 4 对旋式轴流风机基元级速度三角形变化示意图 Fig. 4 Sketch map of velocity triangle in elementary stage for counter rotating axial flow fan |
| 图选项 |
图 4为对旋风机的进口和出口均沿径向,增加第1级和第2级叶轮转速时的速度三角形,实线为标准转速下的速度,虚线为改变后的速度,Cz为轴向进气时气流的绝对速度,C、U和W分别为气流绝对速度、叶轮旋转速度和相对速度,下标1表示进口,下标2表示出口,下标Ⅰ表示第1级叶轮,下标Ⅱ表示第2级叶轮,下标u表示周向分量(后文公式下标同此处),“′”表示转速改变后。
2.1 轮缘功变化分析 单位质量气体轮缘功计算公式为
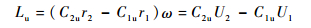 | (1) |
式中:r2和r1分别为出口和进口叶轮半径;ω为叶轮旋转速度。
对单级叶轮而言,可认为叶片进出口半径相同,在转速相同的情况下,旋转速度UⅠ2=UⅠ1记为UⅠ,式(1)可进一步简化为
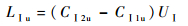 | (2) |
对第1级叶轮而言,将轮缘功公式(2)对UⅠ1求导可得
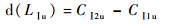 | (3) |
由于CⅠ1u=0,而CⅠ2u>0,可得d(Lu)>0即轮缘功公式与UⅠ正相关,可知增大旋转速度UⅠ可提高第1级叶轮的轮缘功;对第2级叶轮而言,提高第1级叶轮的旋转速度UⅠ,进口速度CⅠ1保持不变时,第1级进口相对速度WⅠ1会增大,WⅠ1与径向的夹角会增大,由于叶型保持不变,从而导致第1级出口相对速度WⅠ2也增大,显然:
 | (4) |
式中:W′Ⅰ1和W′Ⅰ2分别乌1级叶轮速度增大后第1级进口相对速度和第1级出口相对速度。
因此,第1级出口绝对速度CⅠ2会增大,即第2级进口绝对速度CⅡ1增大,在第2级叶轮旋转速度UⅡ保持不变的情况下,第2级进口相对速度WⅡ1会增大,第2级叶轮叶型不变,第2级出口相对速度WⅡ2增大,由于UⅡ不变,第2级出口绝对速度CⅡ2变大,第2级出口绝对速度的周向分量CⅡ2u不再为零,可得
 | (5) |
由速度三角形可知
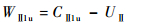 | (6) |
同理将W′Ⅱ1u、W′Ⅱ2u和WⅡ2u分别用绝对速度和周向速度来表示,代入式(5)可得
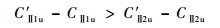 | (7) |
由于第2级叶轮的旋转方向与绝对速度的分量方向相反,因此:
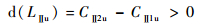 | (8) |
可众2级叶轮的做功也会相应的提高。
在保持流量和UⅠ不变的情况下,提高UⅡ,CⅡ2会沿旋转方向变化,类似于提高UⅠ时,第1级叶轮做功能力的提升,第2级叶轮的做功能力会提高,由于第2级叶轮的进口参数基本无变化,因此第1级叶轮的参数基本保持不变,第1级的做功和效率等参数可认为基本不变。
2.2 气流角变化分析 在保持第2级叶轮旋转速度不变,提高第1级叶轮旋转速度UⅠ后,由于气流的绝对速度CⅠ1不变,导致WⅠ1沿-UⅠ方向增大,此时第1级叶轮进口气流角βⅠ1减小为β′Ⅰ1,记
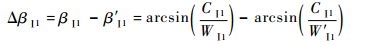 | (9) |
式中:ΔβⅠ1乌1级叶轮进气气流角变化。
则气流迎角i变为
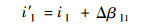 | (10) |
由于ΔβⅠ1>0,所以气流迎角i增大。第1级叶轮出口气流角改变为
 | (11) |
气流落后角δⅠ变为
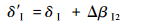 | (12) |
由于ΔβⅠ2>0,所以气流落后角δⅠ也增大。
气流转折角为
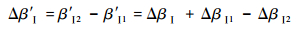 | (13) |
第2级气流迎角和落后角分别为
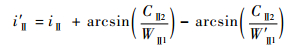 | (14) |
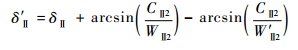 | (15) |
由于WⅡ1<W′Ⅱ1且WⅡ2<W′Ⅱ2,所以第2级的迎角和落后角也会增大。
类似的可知,在保持第1级转速不变,增大第2级转速下,第1级的气流迎角和落后角不变,第2级的气流迎角和落后角增大。
总之,保持第2级叶轮转速不变,提高第1级叶轮转速,第1级和第2级叶轮的做功能力、功率、气流迎角、落后角和转折角均会增大;保持第1级叶轮转速不变,提高第2级叶轮转速,第1级叶轮的参数保持不变,第2级叶轮的做功能力、功率值、气流迎角和落后角会相应的增大。
3 数值计算与实验数据比较和分析 3.1 数值计算与实验数据比较 图 5为转速3 000-3 000计算总压升和总功率与实验对比。从图 5中可以看出随着流量增大,风机的总压升和总功率下降,计算结果与实验吻合较好,计算结果可信。
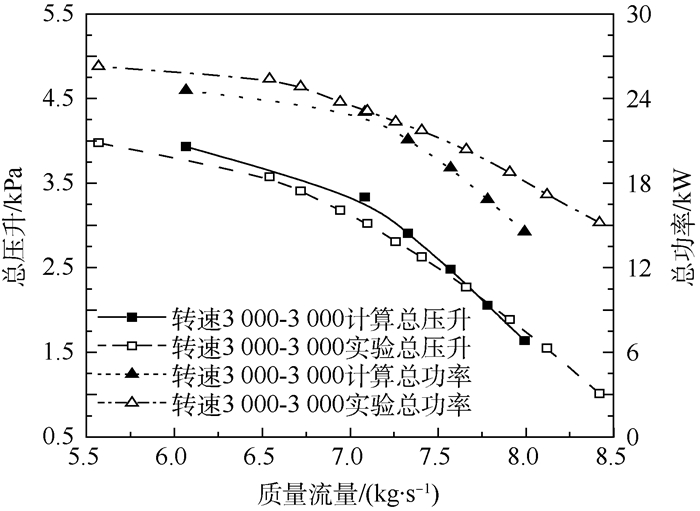 |
| 图 5 转速3 000-3 000计算总压升和总功率与实验对比 Fig. 5 Comparison of calculated and measured total pressurerise and total power under rotating speed 3 000-3 000 |
| 图选项 |
3.2 数值计算结果流场分析 图 6为不同转速下50%叶高处静压云图。比较图 6(a)、图 6(c)和图 6(e)可以看出,随着第1级转速的增加第1级叶轮增压能力逐渐增加;第1级叶轮叶片吸力面前缘附近的低静压区域扩大,第1级叶轮气流在叶片吸力面前缘附近加速增大;叶片滞止点向压力面移动;而第2级叶轮的叶片吸力面前缘附近的低静压区域向压力面移动而叶片滞止点向吸力面移动。这是由于随着第1级叶轮旋转速度的增加,第1级叶轮的进气气流角减小,第2级叶轮的进气气流角减小所导致的,这与速度三角形分析的结果一致。
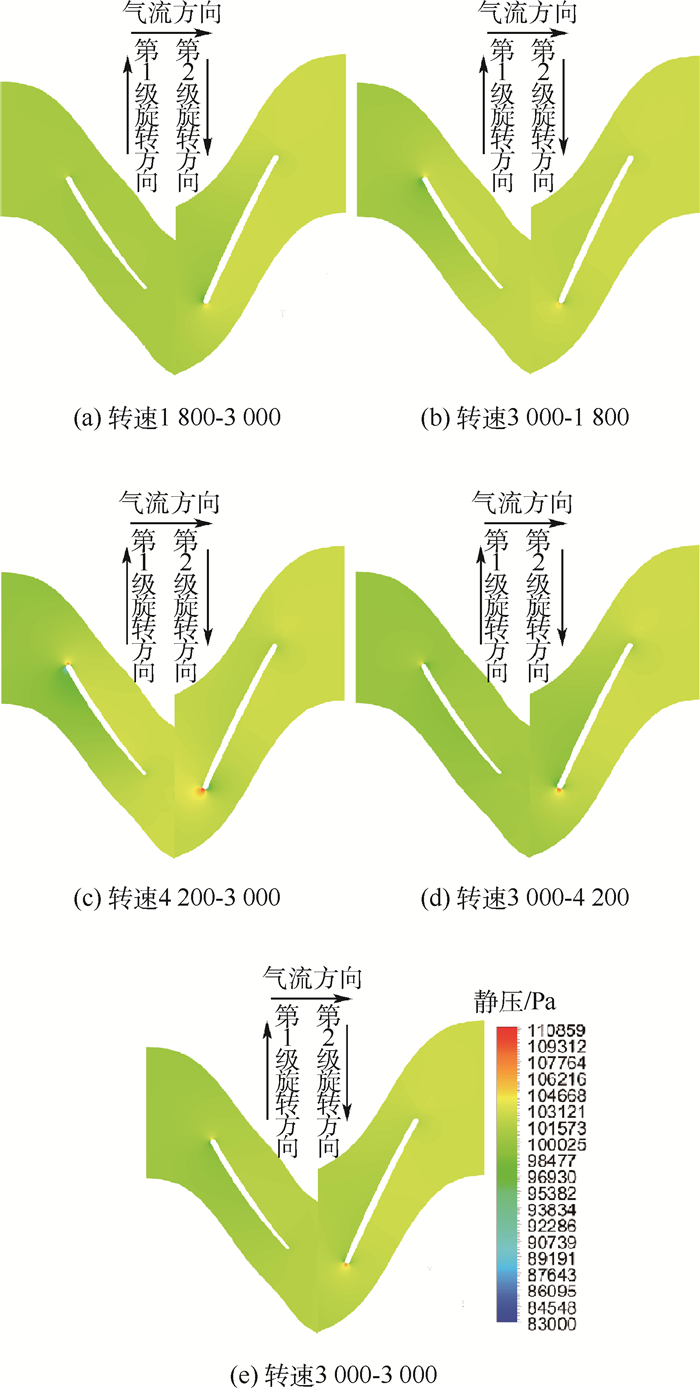 |
| 图 6 不同转速下50%叶高处静压云图 Fig. 6 Contours of static pressure on middle section under different rotating speeds |
| 图选项 |
比较图 6(b)、图 6(d)和图 6(e)可以看出,在保持第1级转速不变的情况下,增大第2级叶轮转速,对第1级流动影响较小,第2级叶轮的变化与增大第1级叶轮旋转速度时第1级叶轮变化一致。
比较图 6(b)和图 6(c)可以看出当第1级叶轮转速高于第2级叶轮转速时,第1级叶轮的低静压区出现在吸力面,第2级叶轮的低静压区出现在压力面,这与图 6(a)和图 6(d)正好相反。
图 7为不同转速下50%叶高处流线图。比较图 7(a)、图 7(c)和图 7(e)可以看出随着第1级转速的增加,第1级进气气流角逐渐减小;有更多的流线经过第1级叶轮前缘点流向第1级叶轮吸力面;而第2级叶轮处流线变化与之相反,这与静压变化的原因相同。
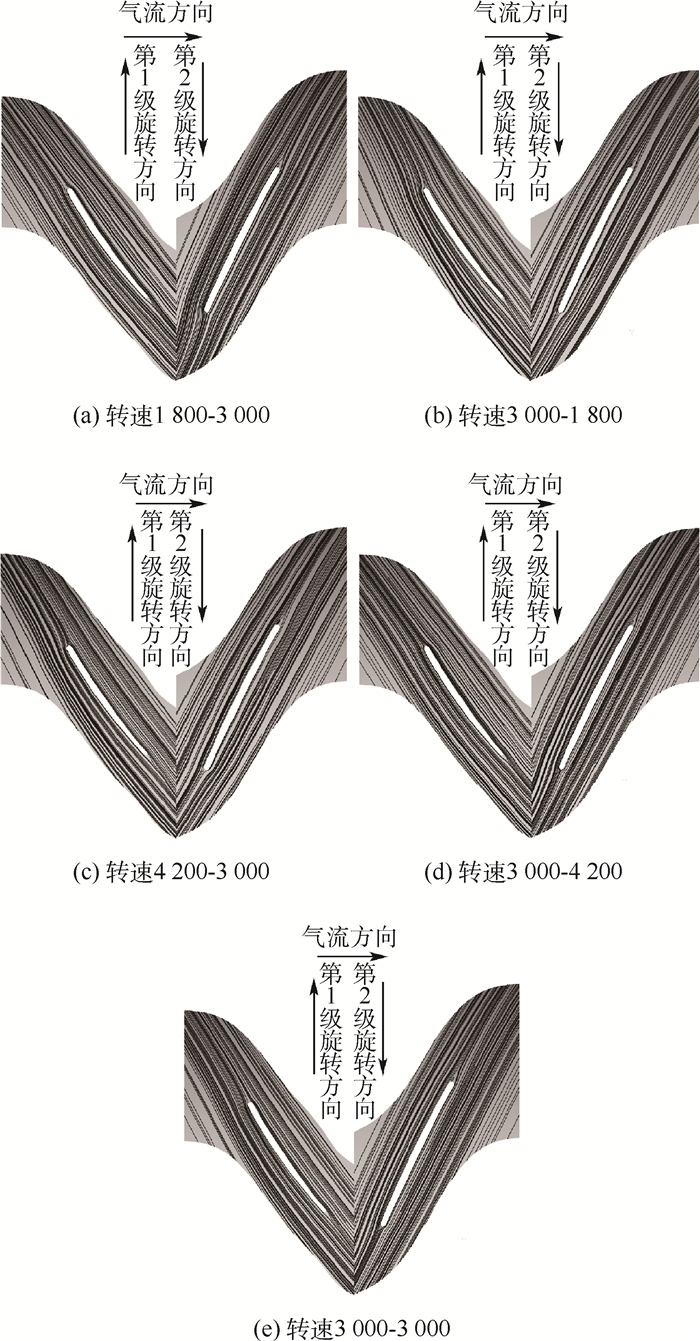 |
| 图 7 不同转速下50%叶高处流线图 Fig. 7 Streamlines on middle section under different rotating speeds |
| 图选项 |
比较图 7(b)、图 7(d)和图 7(e)可以看出,在保持第1级转速不变的情况下,提高第2级叶轮转速,对第1级流动影响较小,第2级叶轮的变化与提高第1级叶轮旋转速度的变化一致,但是相同变化百分比下,第2级叶轮气流变化明显小于提高第1级叶轮旋转速度时第1级叶轮变化。
比较图 7(b)和图 7(c)可以看出当第1级叶轮转速高于第2级叶轮转速时,有更多的流线经过第1级叶轮前缘点流向第1级叶轮吸力面。
3.3 数值计算结果气动特性分析 图 8为风机质量流量、总压升随转速变化曲线。从图 8中可以看到随着转速的增大,风机的质量流量和总压升均增大;第1级叶轮的转速改变对风机的质量流量和总压升的影响比第2级叶轮转速改变的影响大。这与之前速度三角形的分析一致。
 |
| 图 8 风机质量流量、总压升随转速变化曲线 Fig. 8 Curves of mass flow rate and total pressure rise of fan with change of rotating speed |
| 图选项 |
从图 8中还可以看到在小质量流量(小于设计流量7.57 kg/s)下改变第2级叶轮的旋转速度可以获得更高的总压升;而在大质量流量(大于设计质量流量7.57 kg/s)下改变第1级叶轮的旋转速度可以获得更高的总压升。
图 9为风机第1、2级总压升随转速变化曲线。从图 9中可以看到在保持第2级转速不变的情况下,增加第1级叶轮的转速第1级叶轮内的总压升显著提高,而第2级叶轮内的总压升下降,第1级叶轮内增加的总压升大于第2级内下降的总压,因此风机整体的压力上升;这与图 8的结果相一致。在保持第1级转速不变的情况下,增加第2级叶轮的转速有着类似的结论。
 |
| 图 9 风机第1、2级总压升随转速变化曲线 Fig. 9 Curves of total pressure rise of first and second stages of fan with change of rotating speed |
| 图选项 |
图 10为风机总功率随转速变化曲线。从图 10中可以看出随着转速的增加,风机的总功率是增加的;第1级叶轮的转速改变对风机总功率的影响比改变第2级叶轮转速大。
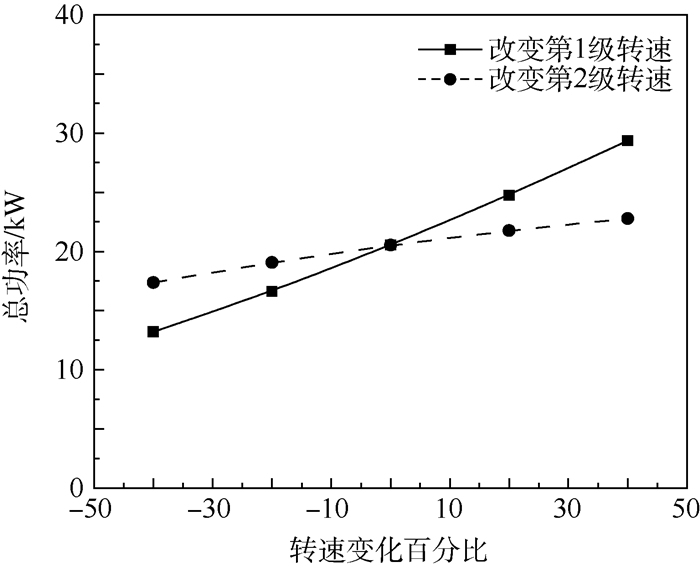 |
| 图 10 风机总功率随转速变化曲线 Fig. 10 Curves of total power of fan with change of rotating speed |
| 图选项 |
图 11为风机第1、2级轴功率随转速变化曲线。从图 11中可以看出在保持第2级转速不变的情况下,增加第1级叶轮的转速第1级叶轮的轴功率显著提高,而第2级叶轮内的轴功率下降,第1级叶轮内增加的功率大于第2级内下降的功率,因此风机整体的压力上升;这与图 10的结果相一致。在保持第1级转速不变的情况下,增加第2级叶轮的转速有着类似的结论。
 |
| 图 11 风机第1、2级轴功率随转速变化曲线 Fig. 11 Curves of shaft power of first and second stages with change of rotating speed |
| 图选项 |
在实际使用过程中前后两级转子的功率差不会太大,且转子功率应在工作在所使用的电机的一定范围以上。可联立方程组:
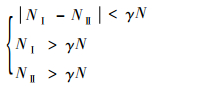 | (16) |
式中:NⅠ和NⅡ分别乌1级和第2级转子的轴功率;γ为轴功率相对于电机的裕度,此处取0.5;N午机功率,此处为11 kW。
求得5.5 kW<NⅠ<11 kW,5.5 kW<NⅡ<11 kW,结合图 11,可知最佳转速百分比乌1级改变10 %时,前后两级叶轮的转速比为1.1:1。
图 12为风机效率随转速变化曲线。图中的效率为考虑传动效率为88.4%的情况下的效率值。从图 12中看到在设计转速下,改变第1级的叶轮转速效率会得到提高,这是因为设计中为了提高风机的高效工作范围并未使设计点处于最高效率处。结合图 11的分析,在前后两级叶轮转速比1.1:1时效率为75%是可以接受的效率。
 |
| 图 12 风机效率随转速变化曲线 Fig. 12 Curves of fan efficiency with change of rotating speed |
| 图选项 |
4 结论 本文通过对旋风机进行数值计算并与实验数据比较后得到在低速流动(低于0.4 Ma)且增压比不高(低于1.1)条件下:
1) 通过对速度三角形的分析与数值计算可知,保持第2级叶轮转速不变,增大第1级叶轮转速,两级叶轮的功率以及气流迎角和落后角都会增大;保持第1级叶轮转速不变,增大第2级叶轮转速,第1级叶轮的参数保持不变,第2级叶轮的功率和相应气流角会增大。
2) 根据数值计算结果可知在保持第2级叶轮转速不变的情况下,提高第1级叶轮的旋转速度,气流进口角减小,滞止点向压力面移动,第2级变化与之相反;保持第1级叶轮转速不变,提高第2级叶轮转速,第1级变化较小,第2级的滞止点向压力面移动。
3) 改变相同百分比下,第1级叶轮转速改变对风机的流量和总压升的影响比改变第2级叶轮的影响大。
4) 结合实际使用以及轴功率随前后两级叶轮转速改变曲线图,确定了风机的最佳转速比为1.1:1,传动效率为88.4%下对旋风机效率为75%。
致谢
本文的实验数据由湖南湘潭平安电气股份有限公司提供,在此表示感谢。
参考文献
| [1] | ROY B, RAVIBABU K, RAO P S, et al. Flow studies in ducted twin-rotor contra-rotating axial flow fans[C]//Proceedings of International Gas Turbine and Aeroengine Congress and Expositon.New York:ASME, 1992:V001T01A131.https://www.researchgate.net/publication/300905187_Flow_Studies_in_Ducted_Twin-Rotor_Contra-Rotating_Axial_Flow_Fans |
| [2] | PUNDHIR D S, SHARMA P B. A study of aerodynamic performance of a contra-rotating axial compressor stage[J].Defence Science Journal, 1992, 42(3): 191–199.DOI:10.14429/dsj.42.4381 |
| [3] | 陈云永, 刘波, 谢彦文. 对转压气机特性影响因素分析研究[J].工程热物理学报, 2010, 31(7): 1121–1126. CHEN Y Y, LIU B, XIE Y W. The investigation of factor affecting performance of a contra-rotating compressor[J].Journal of Engineering Thermophysics, 2010, 31(7): 1121–1126.(in Chinese) |
| [4] | 杨小贺, 单鹏. 两类对转风扇的设计与气动特征数值研究[J].航空动力学报, 2011, 26(10): 2313–2322. YANG X H, SHAN P. Aerodyna-mic design and investigation of two counter-rotating fans[J].Journal of Aerospace Power, 2011, 26(10): 2313–2322.(in Chinese) |
| [5] | 高丽敏, 苗芳, 李晓军, 等. 对转压气机转速比对最先失速级的影响[J].应用力学学报, 2013(6): 845–848. GAO L M, MIAO F, LI X J, et al. Effect of rotating speed ratio on the first rotating stall stage in contra-rotating compressor[J].Chinese Journal of Applied Mechanics, 2013(6): 845–848.DOI:10.11776/cjam.30.06.A039(in Chinese) |
| [6] | MISTRY C, PRADEEP A M. Experimental investigation of a high aspect ratio, low speed contra-rotating fan stage with complex inflow distortion[J].Propulsion & Power Research, 2014, 3(2): 68–81. |
| [7] | 王卓奇, 陆利蓬, 袁巍, 等. 对旋风扇不同转速匹配对失速关键级影响实验[J].北京航空航天大学学报, 2014, 40(6): 797–802. WANG Z Q, LU L P, YUAN W, et al. Experimental investigation on critical stall stage of counter-rotating fan at different speed ratio[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(6): 797–802.(in Chinese) |
| [8] | ZHANG H, HUANG X, ZHANG X. Investigation of unsteady effects on a two-stage counter-rotating fan[J].Procedia Engineering, 2015, 126: 358–361.DOI:10.1016/j.proeng.2015.11.211 |
| [9] | WANG Y C, YUE S Y, CHEN J X, et al.Experimental investigation of unsteady tip clearance flow in a counter-rotating fan[C]//ASME Turbo Expo 2015:Turbine Technical Conference and Exposition.New York:ASME, 2015:V001T09A016.https://www.researchgate.net/publication/299925264_Experimental_Investigation_of_Unsteady_Tip_Clearance_Flow_in_a_Counter-Rotating_Fan |
| [10] | CHO L, CHOI H, LEE S, et al.Numerical and experimental analyses for the aerodynamic design of high performance counter-rotating axial flow fans[C]//ASME 2009 Fluids Engineering Division Summer Meeting.New York:ASME, 2009:231-244.http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=1637813 |
| [11] | 艾子健, 秦国良, 和文强, 等. 对旋风机变工况下两级叶轮变转速匹配研究[J].哈尔滨工程大学学报, 2016, 37(4): 592–597. AI Z J, QIN G L, HE W Q, et al. Speed matching of two-stage impeller with counter-rotating fan under variab le operating conditions[J].Journal of Harbin Engineering University, 2016, 37(4): 592–597.(in Chinese) |
| [12] | WANG J, RAVELET F, BAKIR F.Influence of design parameters on the global performances of low-speed counter-rotating axial-flow fans[C]//ASME 2014, Joint US-European Fluids Engineering Division Summer Meeting and International Conference on Nanochannels, Microchannels, and Minichannels.New York:ASME, 2014:V01BT10A045.https://www.researchgate.net/publication/260005924_Influence_of_Design_Parameters_on_the_Global_Performances_of_Low-Speed_Counter-Rotating_Axial-Flow_Fans |
| [13] | 刘波, 侯为民, 陈云永, 等. 对转压气机转差特性试验与数值模拟[J].航空动力学报, 2009, 24(2): 403–408. LIU B, HOU W M, CHEN Y Y, et al. Experiment and numerical simulation of rotating-speed difference effects on a dual-stage counter-rotating compressor flow field and performance[J].Journal of Aerospace Power, 2009, 24(2): 403–408.(in Chinese) |
| [14] | MURTHY B N, JOSHI J B. Assessment of standard k-ε, RSM and LES turbulence models in a baffled stirred vessel agitated by various impeller designs[J].Chemical Engineering Science, 2008, 63(22): 5468–5495.DOI:10.1016/j.ces.2008.06.019 |
| [15] | BIANCO V, KHAIT A, NOSKOV A, et al. A comparison of the application of RSM and LES turbulence models in the numerical simulation of thermal and flow patterns in a double-circuit RanqueHilsch vortex tube[J].Applied Thermal Engineering, 2016, 106: 1244–1256.DOI:10.1016/j.applthermaleng.2016.06.095 |
