从Sobey[5]在槽道内定常流和振荡流的实验中提出涡波流场以来,Hall和Smith[6]对一个黏性弯槽道内的涡波流场进行了分析,认为在小扰动幅值的情况下,两列波和一个涡相互作用较为剧烈,而高扰动幅值下波和涡旋的相交角度小于41.6°时涡旋趋于分裂直至消失。Nishimura和Matsune[7]从仿真角度研究了二维波状壁面槽道内流体的速度特性,发现波状壁面导致流体在涡旋和主流之间脉动,流体中涡旋的强度随着时间发生变化,在速度为零时涡量最大,时间平均涡流强度和壁剪切应力随着流体的振荡频率增加而增加等流动特性。
目前,对于槽道内涡波流场的深入研究主要基于槽道内流场的涡识别[8-11]及其结构[12-15]的研究成果,特别是针对涡波流场的涡旋的产生机制依赖于目前描述槽道内流场边界层的2种模型,即流向涡包结构模型[16]和拟序结构模型[17]。其中流向涡包结构模型认为流动结构的产生是通过自身的诱导、自组织以及和其他涡包的相互合并而来的;拟序结构模型认为涡旋的产生与湍流边界层中存在2种相反的重要流动结构(喷射和扫掠)在法向方向传输动量,产生雷诺应力导致的剪切运动有关。而湍流边界层外区中的基本结构——发卡涡模型已被广泛接受,Adrian等[16]通过PIV实验认为发卡涡以涡包形式存在,阐明了这些涡包与喷射和扫掠现象的关系以及边界层中低速条带的成因。蒋平等[18]对矩形射流流动过程进行了三维大涡模拟,表明在矩形射流的发展区中流向涡才开始逐渐增强, 在射流中远场流向涡和展向涡在涡强度、前后涡间距等方面大致相当,流体在横截面上不同流向涡之间的游走极大地强化了射流的混合过程。陈云祥等[19]数值分析了层流圆管潜射流在密度均匀黏性流体中的演化机理及其表现特征。郭广明等[20]基于大涡模拟和光线追踪方法, 对光线穿越流场后的光程分布与混合层流场中涡结构之间的关系进行了分析, 提出了一种基于涡核位置提取的涡结构瞬时对流速度定量计算方法,阐述了混合层流场中涡结构对流速度的特性及其机理。
可见槽道内涡波流场的研究主要集中于流场中涡旋的形成[10, 15, 21-24]及其与波状主流的相互作用效应[17, 25-27]上,对边界层外区涡旋的结构以及变化规律鲜有报道。因而本文利用2DPIV技术对槽道内的低雷诺数流场进行瞬态速度矢量测量,分析边界层外区存在的发卡涡以涡包形式的展向涡分布特征,从展向涡的尺度属性、力学属性和运动属性方面探讨展向涡在流场中的变化趋势。
1 实验装置和方法 实验流体为25#变压器油,采用叶片泵(型号为VP-08F-A3,最大转速为1 800 r/min)输出动力;采用横截面为44 mm×44 mm、长为500 mm的矩形槽道,槽道的顶面和前面用有机玻璃制作以进行2DPIV测量槽道内涡波流场的瞬态速度矢量场,测量的位置距入口300 mm;槽道中心主流的速度为V0=0.036 2 m/s,相应的雷诺数为Re=V0D/ν=138.3,D为矩形槽道的等效直径,ν为25#变压器油的运动黏度,则槽道内流体为层流形态。实验系统如图 1所示,以2DPIV测量区域的左下角为原点建立笛卡儿坐标系,x轴方向为槽道内流体的流向方向,y轴方向为流场的法向方向,指向槽道的顶面,z轴方向为流场的展向,垂直于x-y平面,指向槽道的背面。
 |
| 图 1 实验系统 Fig. 1 Experimental system |
| 图选项 |
2DPIV(TSI公司的粒子图像测速系统)用来测量槽道内展向的瞬态速度矢量场,由于变压器油中含有平均粒径为25 μm的悬浮颗粒,具有良好的跟随性以及均匀分布的光散射性,因而2DPIV测量中不需另加示踪粒子。双钕:钇铝石榴石激光器(200 mJ,脉冲频率15 Hz, 532 nm激光波长)发出的激光经过导光臂、片光源镜头(焦距30~3 000 mm,2套圆柱透镜-15 mm F.L.和-25 mm F.L.,发散角分别为25°和14°)形成1 mm厚的片光,从流场的法向方向照射,通过设置在槽道展向方向的Nikon CCD相机(15帧/s,50 mm/F1.8镜头,2K pixel×2K pixel分辨率,1 K=1 024)获取流场的图像信息;激光器、片光源镜头及CCD相机通过三维坐标架实现拍摄区域位置的精确控制,且由同步控制器(时间分辨率0.25 ns)实现激光器、相机拍摄的同步触发;对槽道内的涡波流场获取了200对图像。
粒子图像分析采用先进的多重网格迭代互相关图以及多重自适应变形窗口算法,在图像查询区采用流场流向方向和法向方向上初始查询窗口72 pixel×64 pixel、最终查询窗口64 pixel×48 pixel并50%交叠来获取原始速度矢量以消除查询窗口边界的影响;对错误矢量用一个局部平均验证方法使其临近的5 pixel×5 pixel范围内的均值来替代;并对处理后的矢量场进行进一步互相关峰值的高斯拟合,使获取的速度场能够真实反映槽道内涡波流场流动瞬态信息。
2 展向涡的识别 目前,有关流场边界层涡旋的识别方法主要是基于局部速度梯度张量实现的[10, 28-30],包括Q准则、Δ准则、λci准则、λ2准则,这些准则由严格的数学推导而来,具有一定的物理意义,将流场中的涡旋和剪切层分离。而根据Robinson旋涡的定义:区域存在涡旋是以一定的速度跟随涡旋中心观察,流线在与涡旋方向垂直的平面上的投影呈现出螺旋图案的情况。说明涡旋通常会以一定的速度对流,需要考虑伽利略不变性。Adrian等[16]认为当涡旋以长时平均速度运动时,通过雷诺分解可将涡旋清晰展示出来。因而在槽道内边界层外区的涡旋识别中采用雷诺分解,以获取局部脉动速度场,再利用局部速度梯度的共轭复特征值的虚部来表示旋转强度的λci准则进行识别。
首先,利用旋转强度Λci=λciωz/|ωz|的正负符号表征不同旋向的涡,Λci为涡的旋转强度,ωz为展向涡的涡量。然后,将λci准则的阈值设定[31]为|Λci(x, y)|≥1.5Λcirms(y),Λcirms(y)为涡的旋转强度沿法向位置的均方根值。
图 2为利用旋转强度的λci准则对槽道内涡波流场中展向涡的识别结果。图中:横纵坐标为2DPIV测量范围的尺度与槽道法向距离的比值,fs=7.5 Hz为2DPIV测量脉冲频率;色度条表示流场的涡量大小,箭头表示流场的速度矢量,封闭的实线表示λci准则识别的展向涡区域,实线的颜色与流场的局部涡量颜色一致,分别表征顺时针展向涡和逆时针展向涡。图 2中:t=0/fs, 3/fs, 5/fs, 7/fs分别表示PIV采集的槽道内涡波流场的时间,即流场的序数与脉冲频率的比值。
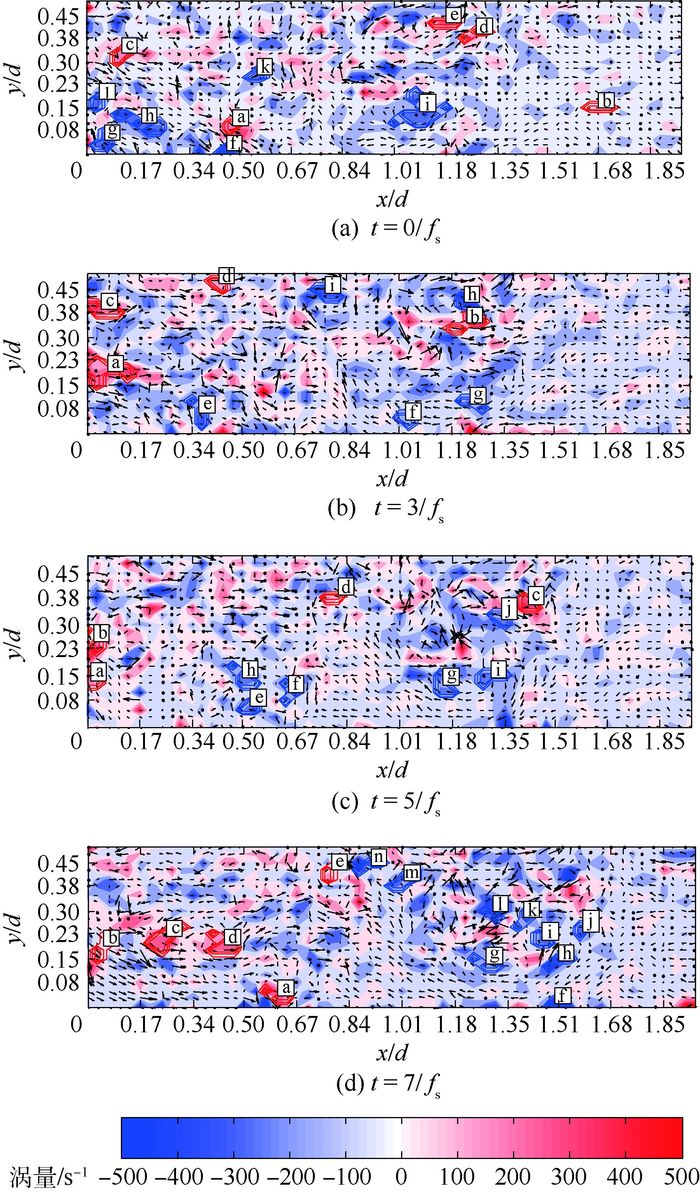 |
| 图 2 涡波流场的展向涡λci准则识别结果 Fig. 2 Identification results of spanwise vortex λci criteria in vortex wave field |
| 图选项 |
从图 2中可以看到,展向涡位于流场中涡量集中的区域,其中展向涡区域的速度矢量呈现出螺旋旋转特征;流场中展向涡的数量较多,且顺时针展向涡的数量大于逆时针展向涡的数量;随着槽道内流体流动时间的延长,流场左端尺度较小的展向涡在波状主流的作用下逐渐集中,且旋向相反的展向涡互相交融;由于不同旋向的展向涡数量不同,从而宏观上使流场部分区域呈现了旋向一致的展向涡,如图 2(d)中标识为f—l的顺时针展向涡集中在一起形成一个宏观尺度较大的顺时针展向涡。
3 展向涡的平均属性 3.1 展向涡的尺度属性分布 为了描述槽道内涡波流场展向涡的尺度属性,根据2DPIV测量实验的设置方案,取与λci准则识别的展向涡区域具有相同面积圆的直径,作为展向涡的等效直径,经过流向和时间平均得到法向平均直径:
 | (1) |
式中:dr(x, y, t)和dp(x, y, t)分别为某一时刻流场经过λci准则识别的逆时针展向涡和顺时针展向涡的等效直径;C和L分别为2DPIV测量的流向和法向速度点的个数;N为2DPIV测量的流场数;〈Dr〉和〈Dp〉分别为逆时针展向涡和顺时针展向涡的平均直径。
图 3(a)为逆时针展向涡和顺时针展向涡的平均直径随流场法向的变化规律,可见在流场边界层外区展向涡的平均直径在法向0.05和0.45处产生急剧变化,这是由于计算流场展向涡的平均直径受到2DPIV测量区域边界的限制造成统计数量不足的结果;从法向位置0.05~0.45范围内看,逆时针展向涡随着法向位置的增加,其平均直径缓慢增加,相反,顺时针展向涡的平均直径则随着法向位置的增加而趋于下降,且在法向位置0.10处,低于此值的区域顺时针展向涡的平均直径大于逆时针展向涡的平均直径,反之,则顺时针展向涡的平均直径小于逆时针展向涡的平均直径。由于2DPIV测量的流场区域位于波状主流的中心,与边界层的展向涡平均直径变化不同,在此区域涡旋的尺度在波状主流的作用下会增大[32],而顺时针展向涡与波状主流的方向一致,致使在0.10~0.45法向范围内顺时针展向涡的平均直径小于逆时针展向涡的平均直径,且有下降的趋势。
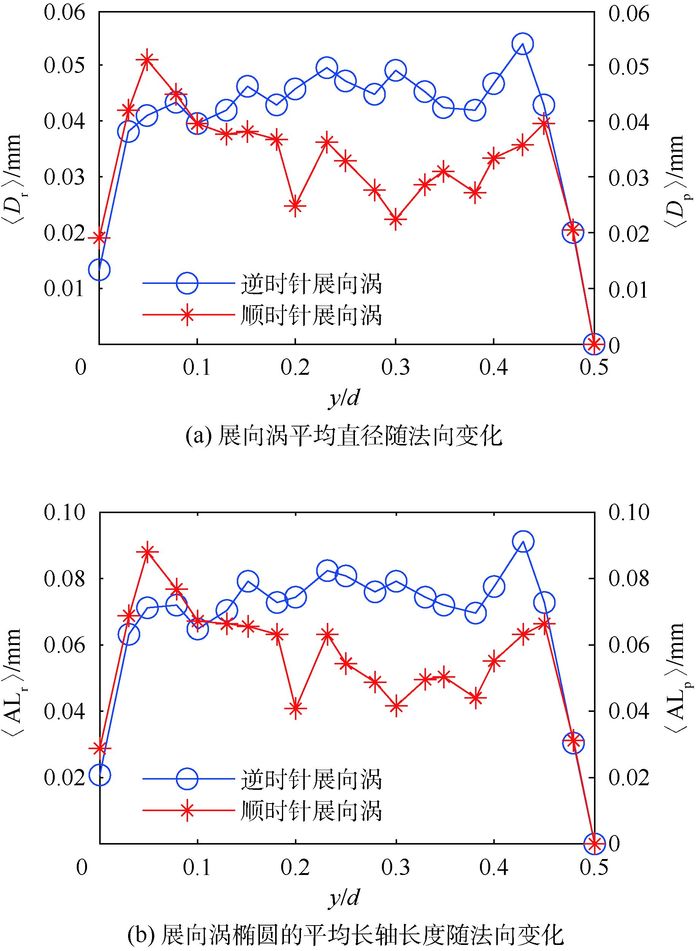 |
| 图 3 展向涡的平均直径和平均长轴长度 Fig. 3 Mean diameter and mean length of long axis of spanwise vortex |
| 图选项 |
同理,将λci准则识别的展向涡区域等效为具有相同标准二阶中心矩的椭圆的长轴长度,经过流向和时间平均得到椭圆的平均长轴长度即为展向涡的平均长轴长度〈ALr〉、〈ALp〉,则平均长轴长度随法向位置变化的情况如图 3(b)所示。
可见,展向涡的等效椭圆的平均长轴长度与图 3(a)的平均直径的变化基本一致,这是由于经过λci准则识别的展向涡区域是一定的,只是将其转换为不同的表达方式。
利用展向涡的等效椭圆的表征方法,可获取相应区域的等效椭圆长轴与流向的交角(倾角)以及等效椭圆的离心率,分别称为展向涡的长轴倾角和离心率,则展向涡的长轴倾角〈IAr〉、〈IAp〉和离心率〈er〉、〈ep〉随法向位置的变化分别如图 4(a)、(b)所示。
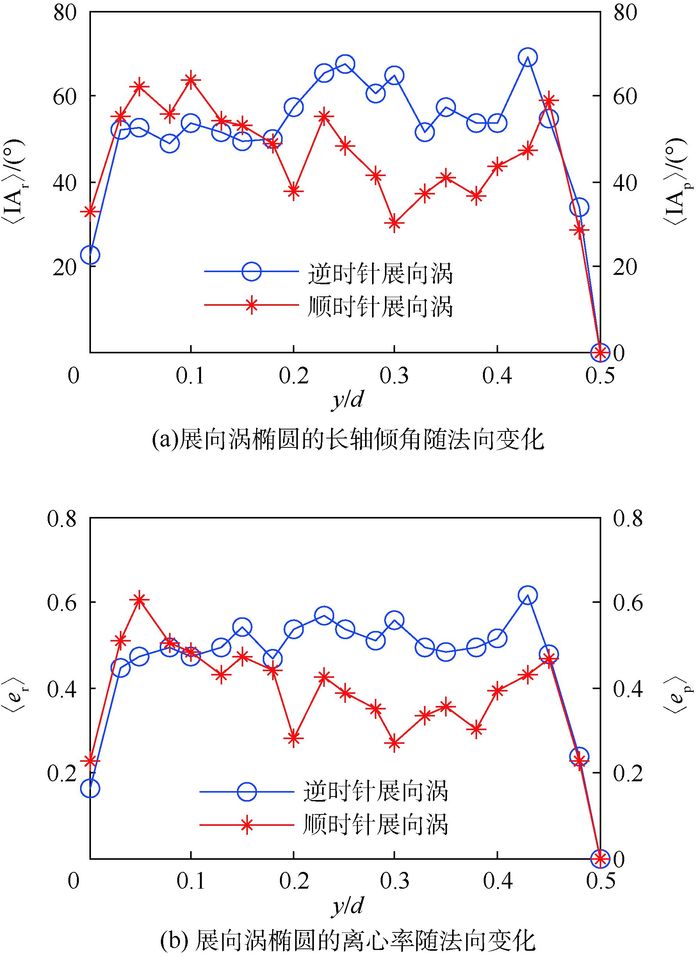 |
| 图 4 展向涡的长轴倾角和离心率 Fig. 4 Long axis inclination angle and eccentricity of spanwise vortex |
| 图选项 |
由图 4(a)可以看出,在0.10~0.40法向范围内,逆时针展向涡的椭圆长轴与流向的交角在中间位置0.20~0.30较大,最大值为67.28°,其他法向位置的交角在50°上下变化;顺时针展向涡的椭圆长轴倾角在0.10~0.40法向范围内变化幅度较大,基本呈下降趋势。从图 2可以看出,逆时针展向涡相对于顺时针展向涡分散性较大,且数量较少,因而逆时针展向涡受波状主流的影响相对较小,其长轴倾角在法向中间位置之外的变化较为稳定。
受波状主流的影响,顺时针展向涡的等效椭圆的离心率变化幅度较大,在法向位置0.05~0.45范围内呈下降趋势,如图 4(b)所示,即顺时针展向涡的似圆性较好;反之逆时针展向涡的等效椭圆的离心率在法向位置0.05~0.45范围内在0.5上下波动。
3.2 展向涡的力学属性分布 由于在流场强剪切区域的流体微团并没有发生旋转,但仍有较大的涡量,图 2中标识符号的区域是λci准则识别的展向涡区域,也是流场涡量较为集中的区域,但是流场涡量较大的区域并没有全部被识别为展向涡区域。
将λci准则识别的展向涡的旋转强度Λci经过流向和时间平均得到逆时针展向涡和顺时针展向涡的旋转强度随法向位置变化的情况,见图 5(a)。
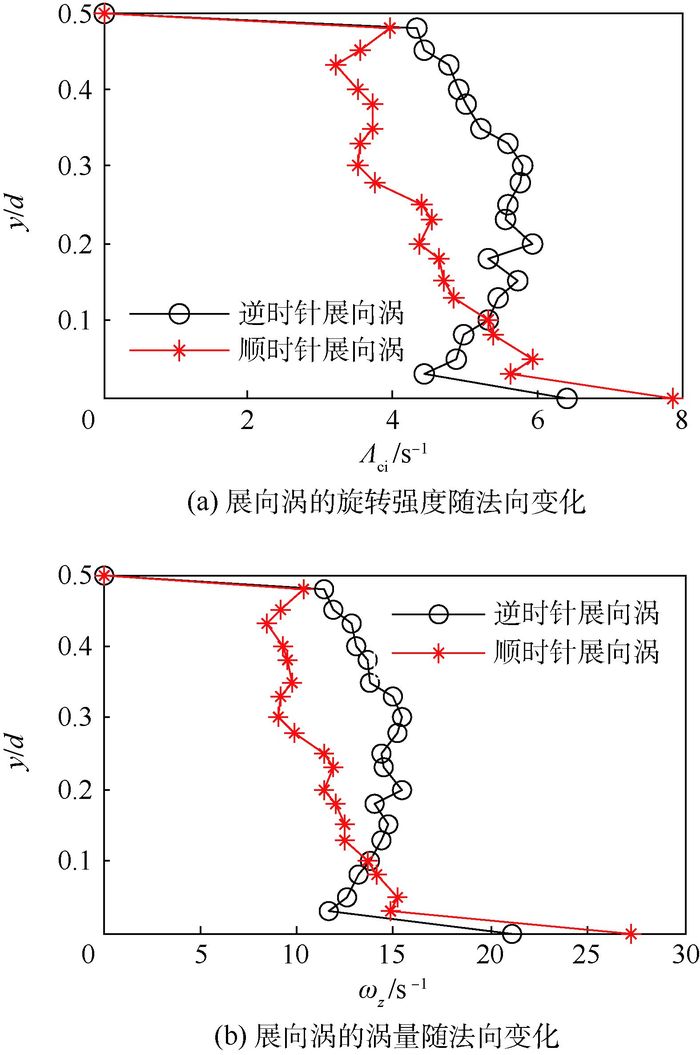 |
| 图 5 展向涡的旋转强度和涡量 Fig. 5 Rotational strength and vorticity of spanwise vortex |
| 图选项 |
可以看出,在0.05~0.45法向位置范围内,逆时针展向涡的旋转强度呈抛物线形状变化,在法向位置0.20处达到最大值5.9,而顺时针展向涡在0.05~0.45法向位置范围内整体呈下降趋势,且顺时针展向涡在0.10~0.45法向位置范围内的旋转强度低于逆时针展向涡。从图 5(b)也可看出,逆时针展向涡涡量的幅值在0.10~0.45法向位置范围内同样大于顺时针展向涡的涡量;且同样法向位置处展向涡的涡量约是涡旋旋转强度的3倍。
则展向涡和涡量之间的这种关系可用不同旋向的展向涡对〈vωz〉的全局平均分量表示[33]:
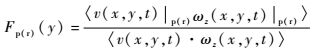 | (2) |
式中:v(x, y, t)|p(r)和ωz(x, y, t)|p(r)分别为λci准则识别的逆时针(顺时针)展向涡区域内的法向速度和涡量。
图 6(a)为逆时针展向涡和顺时针展向涡对全局平均的〈vωz〉分量Fr、Fp随法向位置的变化情况。可见,逆时针展向涡对全局平均的〈vωz〉分量在法向位置0.10~0.30范围内先下降再增加后下降,在0.33~0.48法向位置范围内随之缓慢增加,在0.15处出现最大值61%;与之相反,顺时针展向涡对全局平均的〈vωz〉分量在0.10处先达到最大值57%后再急剧下降直至法向位置0.18处,随后呈缓慢增加趋势;与流场边界层的展向涡对全局平均的〈vωz〉分量变化趋势不同[33],图 6(b)所示的展向涡是在流场的边界层外区,且流场的雷诺数较低,因而其对全局平均的〈vωz〉分量在法向位置0~0.18范围内的变化幅度较大。
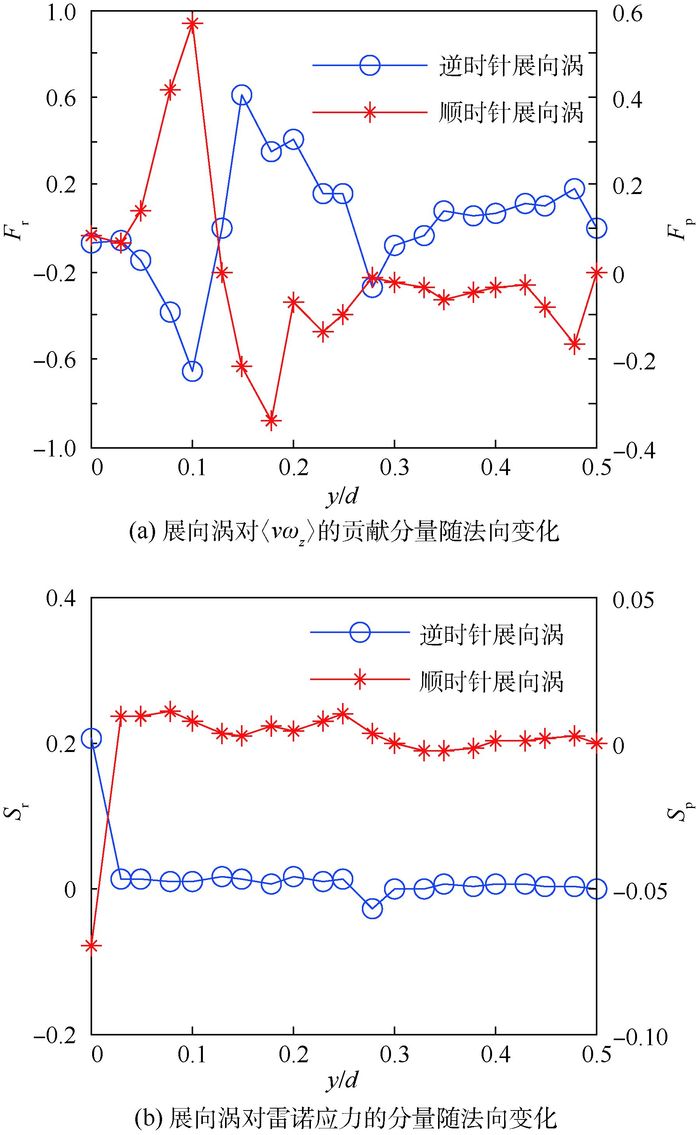 |
| 图 6 展向涡对的〈vωz〉分量和雷诺应力分量 Fig. 6 〈vωz〉 component and Reynolds stress component of spanwise vortex pair |
| 图选项 |
同理,为了表征展向涡对整体雷诺应力的影响,建立展向涡与雷诺应力的表达式为
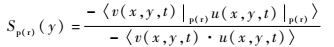 | (3) |
式中:u(x, y, t)|p(r)为λci准则识别的逆时针(顺时针)展向涡区域内流场的流向速度。
图 6(b)为逆时针展向涡和顺时针展向涡对整体雷诺应力Sr、Sp的影响随法向位置的变化情况。可见,去除展向涡的测量边界影响点(法向位置0处)后,逆时针展向涡对流场雷诺应力的影响较小,整体呈缓慢下降趋势,最大值在法向位置0.03处为1.1%;顺时针展向涡对流场雷诺应力的影响同样在法向位置0.03处有最大值0.9%,整体也呈下降趋势。这是由于不同旋向的展向涡自身是一个严实的小体积,仅对局部雷诺应力有影响,对整体雷诺应力的影响由于不同旋向而抵消,还有****认为流场的雷诺应力是展向涡的诱导行为,因而对其影响较小[16]。
3.3 展向涡的运动属性分布 根据Wu和Christensen[31]定义的展向涡数量密度,来描述流场展向涡的数量增长趋势。展向涡的数量密度Πp(r)(y)是用展向涡涡心法向位置的3倍法向间距Δy/d与流向距离x/d窗口面积内的展向涡的整体平均数Np(r)(y)来表示:
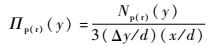 | (4) |
式中:d为槽道的法向距离。
图 7(a)为展向涡的数量密度随流场法向位置的变化情况。可以看到,逆时针展向涡的数量密度在0~0.08法向位置范围内呈急剧上升趋势,并达到最大值0.36,随后0.08~0.43法向位置范围内缓慢下降,最后又急剧下降;顺时针展向涡与之不同的是,其数量密度整体呈倒U形分布,与图 2一致表明顺时针展向涡的数量大于逆时针展向涡的数量,在法向位置的中心区域,受波状主流的影响,顺时针展向涡得到激发而增加,但是其尺度相对于逆时针展向涡较小。
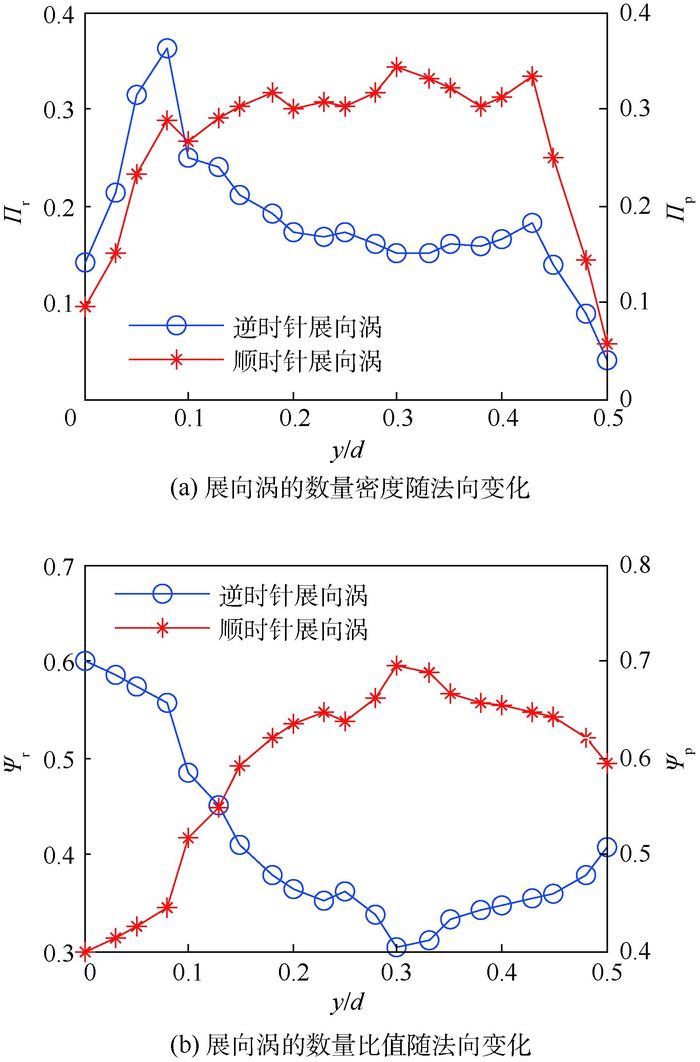 |
| 图 7 展向涡的数量密度和数量比值 Fig. 7 Population density and quantity ratio of spanwise vortex |
| 图选项 |
利用展向涡占总展向涡数量的比值,即数量比值来分析不同旋向的展向涡的数量密度的变化趋势,则展向涡的数量比值为
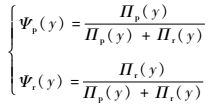 | (5) |
式中:Ψr(y)和Ψp(y)分别为逆时针展向涡和顺时针展向涡占总展向涡数量的比值。
不同旋向展向涡的数量比值随法向位置的变化如图 7(b)所示,可见,不同旋向展向涡占总展向涡数量密度的比值都大于0.3。其中,逆时针展向涡的数量比值在法向位置0~0.30范围内呈下降趋势,随后又逐渐上升;顺时针展向涡的数量比值与之相反。表明槽道中心区域的波状主流对展向涡的数量影响较大。
根据λci准则识别的展向涡涡心坐标以及雷诺分解的原理,可以得到各个涡心的速度,则由Robinson旋涡的定义可知,所获取涡心的速度可表征展向涡的对流速度。
图 8为展向涡对流速度随法向位置变化的情况。图 8(a)为展向涡的流向对流速度〈Uc〉与流场的平均流向速度随法向位置的变化,图 8(b)为展向涡的法向对流速度〈Vc〉随法向的变化。由图 8(a)可见,展向涡的流向对流速度整体上小于流场的平均速度,且在槽道中心区域差值较大;由图 6可知,在这个法向范围内展向涡对全局平均的〈vωz〉分量幅值变化较大,再结合图 8(b)展向涡法向对流速度基本为负值,此范围内的展向涡发生类似湍流边界层中的“扫掠”现象,而法向位置0.30~0.50范围内展向涡的流向对流速度低于平均速度,且法向对流速度为正值,此范围内的展向涡发生类似湍流边界层中的“喷射”现象。
 |
| 图 8 展向涡的对流速度 Fig. 8 Convective velocity of spanwise vortex |
| 图选项 |
图 8(b)中,展向涡的法向对流速度随着法向距离增加,从负值上升到正值,表明了槽道内涡波流场的波状主流的变化特征,展向涡在波状主流的卷绕下运动,在槽道中心区域,主流流向速度较大,因而展向涡的流向对流速度相对较大,在中心主流两侧分别发生喷射和扫掠2种现象。
4 结论 1) 对槽道内边界层外区的流场采用雷诺分解和旋转强度的λci准则进行了展向涡的识别,流场中的顺时针展向涡的数量大于逆时针展向涡的数量,且随着时间的延长,尺度较小的涡旋在波状主流的作用下发展为较大尺度的展向涡。
2) 在0.05~0.45法向位置范围内,逆时针展向涡的平均直径和椭圆长轴长度随着法向位置的增加而缓慢增加,顺时针展向涡则趋于下降;在0.10~0.45法向范围内,顺时针展向涡的平均直径和椭圆长轴长度小于逆时针展向涡;逆时针展向涡的椭圆长轴倾角在法向位置0.20~0.30较大,最大值为67.28°,顺时针展向涡基本呈下降趋势;顺时针展向涡等效椭圆的离心率呈下降趋势,似圆性较好;逆时针展向涡等效椭圆的离心率在法向位置0.05~0.45范围内在0.5上下波动。
3) 在0.05~0.45法向位置范围内,逆时针展向涡旋转强度呈抛物线形状变化,而顺时针展向涡整体呈下降趋势;逆时针展向涡对全局平均的〈vωz〉分量在法向位置0.10~0.30范围内先下降再增加后下降,在0.15处出现最大值61%;顺时针展向涡对全局平均的〈vωz〉分量在0.10处先达到最大值57%后再急剧下降;逆时针展向涡对流场雷诺应力的影响较小,整体呈缓慢下降趋势,最大值为1.1%;顺时针展向涡在法向位置0.03处有最大值0.9%,整体也呈下降趋势。
4) 逆时针展向涡的数量密度在0~0.08法向位置范围内呈急剧上升趋势,并达到最大值0.36,顺时针展向涡数量密度整体呈倒U形分布;不同旋向的展向涡占总展向涡数量密度的比值都大于0.3;展向涡的流向对流速度整体上小于流场的平均速度,且在槽道中心区域差值较大;展向涡的法向对流速度随着法向距离增加,从负值上升到正值,在中心主流两侧分别发生喷射和扫掠2种现象。
参考文献
| [1] | WANG G, EVANS G M, JAMESON G J. Bubble-particle detachment in a turbulent vortex I:Experimental[J].Minerals Engineering, 2016, 92(6): 196–207. |
| [2] | YUAN H, TAN S, WEN J, et al. Heat transfer of pulsating laminar flow in pipes with wall thermal inertia[J].International Journal of Thermal Sciences, 2016, 99(1): 152–160. |
| [3] | ESCHMANN G, KUNTZE A, UFFRECHT W, et al. Experimental and numerical investigation of heat transfer coefficients in gaseous impinging jets-First test of a recent sensor concept for steady and unsteady flow[J].International Journal of Thermal Sciences, 2015, 96(3): 290–304. |
| [4] | ABIEV R S, GALUSHKO A S. Hydrodynamics of pulsating flow type apparatus:Simulation and experiments[J].Chemical Engineering Journal, 2013, 229(8): 285–295. |
| [5] | SOBEY I J. Observation of waves during oscillation channel flow[J].Journal of Fluid Mechanics, 1985, 151: 395–426.DOI:10.1017/S0022112085001021 |
| [6] | HALL P, SMITH F T. The nonlinear interaction of Tollmien-Schlichting waves and Taylor-Gortler vortices in curved channel flows[J].Proceedings of the Royal Society A:Mathematical, 1988, 417(1853): 255–282.DOI:10.1098/rspa.1988.0060 |
| [7] | NISHIMURA T, MATSUNE S. Vortices and wall shear stresses in asymmetric and symmetric channels with sinusoidal wavy walls for pulsatile flow at low Reynolds numbers[J].International Journal of Heat and Fluid Flow, 1998, 19(6): 583–593.DOI:10.1016/S0142-727X(98)10005-X |
| [8] | BERSON A, MICHARD M, BLANC-BENON P. Vortex identification and tracking in unsteady flows[J].Comptes Rendus Mecanique, 2009, 337(2): 61–67.DOI:10.1016/j.crme.2009.03.006 |
| [9] | CHAKRABORTY P, BALACHANDAR S, ADRIAN R J. On the relationships between local vortex identification schemes[J].Journal of Fluid Mechanics, 2005, 535: 189–214.DOI:10.1017/S0022112005004726 |
| [10] | GRAFTIEAUX L, MICHARD M, GROSJEAN N. Combining PIV, POD and vortex identification algorithms for the study of unsteady turbulent swirling flows[J].Measurement Science and Technology, 2001, 12(9): 1422–1429.DOI:10.1088/0957-0233/12/9/307 |
| [11] | LIU C, WANG Y, TANG J.New vortex identification method and vortex ring development analysis in boundary layer transition[C]//54th AIAA Aerospace Sciences Meeting.Reston:AIAA, 2016:1-28. |
| [12] | LEE J, LEE J H, CHOI J, et al. Spatial organization of large-and very-large-scale motions in a turbulent channel flow[J].Journal of Fluid Mechanics, 2014, 749: 818–840.DOI:10.1017/jfm.2014.249 |
| [13] | NATRAJAN V K, WU Y, CHRISTENSEN K T. Spatial signatures of retrograde spanwise vortices in wall turbulence[J].Journal of Fluid Mechanics, 2007, 574: 155–167.DOI:10.1017/S0022112006003788 |
| [14] | PIROZZOLI S, BERNARDINI M, GRASSO F. Characterization of coherent vortical structures in a supersonic turbulent boundary layer[J].Journal of Fluid Mechanics, 2008, 613(6): 205–231. |
| [15] | YANG W, MENG H, SHENG J. Dynamics of hairpin vortices generated by a mixing tab in a channel flow[J].Experiments in Fluids, 2001, 30(6): 705–722.DOI:10.1007/s003480000252 |
| [16] | ADRIAN R J, MEINHART C D, TOMKINS C D. Vortex organization in the outer region of the turbulent boundary layer[J].Journal of Fluid Mechanics, 2000, 422(13): 1–54. |
| [17] | LOZANO-DURáN A, JIMéNEZ J. Time-resolved evolution of coherent structures in turbulent channels:Characterization of eddies and cascades[J].Journal of Fluid Mechanics, 2014, 759: 432–471.DOI:10.1017/jfm.2014.575 |
| [18] | 蒋平, 郭印诚, 张会强, 等. 矩形射流中的流向涡分布特性及作用[J].清华大学学报(自然科学版), 2005, 45(8): 1110–1113. JIANG P, GUO Y C, ZHANG H Q, et al. Distribution and function of streamwise vortexes in rectangular jet flows[J].Journal of Tsinghua University(Science and Technology), 2005, 45(8): 1110–1113.(in Chinese) |
| [19] | 陈云祥, 陈科, 尤云祥, 等. 层流圆管潜射流生成蘑菇形涡结构特性数值研究[J].物理学报, 2013, 62(11): 114701–114710. CHEN Y X, CHEN K, YOU Y X, et al. Numerical investigation on the characteristics of the mushroom-like vortex structure generated by a submerged laminar round jet[J].Acta Physica Sinica, 2013, 62(11): 114701–114710.DOI:10.7498/aps.62.114701(in Chinese) |
| [20] | 郭广明, 刘洪, 张斌, 等. 混合层流场中涡结构对流速度的特性[J].物理学报, 2016, 65(7): 74701–74702. GUO G M, LIU H, ZHANG B, et al. Characteristics of convective speeds of vortex structures in mixing layer[J].Acta Physica Sinica, 2016, 65(7): 74701–74702.DOI:10.7498/aps.65.074701(in Chinese) |
| [21] | GHOMESHI M, KAMANBEDAST A A. Experimental investigation of height preventing structures for vertical wave against flow in open channel[J].World Applied Sciences Journal, 2010, 9(9): 1067–1074. |
| [22] | KIM K, SUNG H J, ADRIAN R J. Effects of background noise on generating coherent packets of hairpin vortices[J].Physics of Fluids, 2008, 20(10): 105107–1.DOI:10.1063/1.3001797 |
| [23] | ADRIAN R J, CHRISTENSEN K T, LIU Z C. Analysis and interpretation of instantaneous turbulent velocity fields[J].Experiments in Fluids, 2000, 29(3): 275–290.DOI:10.1007/s003489900087 |
| [24] | DEFINA A, PRADELLA I. Vortex-induced cross-flow seiching in cylinder arrays[J].Advances in Water Resources, 2014, 71: 140–148.DOI:10.1016/j.advwatres.2014.06.002 |
| [25] | MONTY J P, STEWART J A, WILLIAMS R C, et al. Large-scale features in turbulent pipe and channel flows[J].Journal of Fluid Mechanics, 2007, 589: 147–156. |
| [26] | PIROZZOLI S, BERNARDINI M, GRASSO F. On the dynamical relevance of coherent vortical structures in turbulent boundary layers[J].Journal of Fluid Mechanics, 2010, 648(10): 325–349. |
| [27] | WOODCOCK J D, MARUSIC I. The statistical behaviour of attached eddies[J].Physics of Fluids, 2015, 27(1): 97–120. |
| [28] | CHEN Q, ZHONG Q, QI M, et al. Comparison of vortex identification criteria for planar velocity fields in wall turbulence[J].Physics of Fluids, 2015, 27(8): 85101.DOI:10.1063/1.4927647 |
| [29] | CHEN Q, ZHONG Q, WANG X, et al. An improved swirling-strength criterion for identifying spanwise vortices in wall turbulence[J].Journal of Turbulence, 2014, 15(2): 71–87.DOI:10.1080/14685248.2014.881488 |
| [30] | HO S.An effective vortex detection approach for velocity vector field[C]//201221st International Conference on Pattern Recognition.Piscataway, NJ:IEEE Press, 2012:2643-2646. |
| [31] | WU Y, CHRISTENSEN K T. Population trends of spanwise vortices in wall turbulence[J].Journal of Fluid Mechanics, 2006, 568(10): 55–76. |
| [32] | GAO Q, ORTIZ-DUEN~AS C, LONGMIRE E K. Analysis of vortex populations in turbulent wall-bounded flows[J].Journal of Fluid Mechanics, 2011, 678(4): 87–123. |
| [33] | CHEN Q, ADRIAN R J, ZHONG Q, et al. Experimental study on the role of spanwise vorticity and vortex filaments in the outer region of open-channel flow[J].Journal of Hydraulic Research, 2014, 52(4): 476–489.DOI:10.1080/00221686.2014.919965 |
