搅拌流是竖直管或近似竖直的倾斜管内的典型流型,主要发生在弹状流向环状流的转变区域内[1-3]。搅拌流内液膜振荡剧烈,存在气液逆向流动和液泛等特殊的动力学现象;气液界面分布着大振幅界面波(下文简称大波),大波在运动过程中受气流作用产生夹带液滴,以及液滴重新沉积到液膜表面等传质过程[4-5]。在管内沸腾流动与传热过程中,搅拌流动时发生剧烈液膜失稳和液滴夹带现象,以及流型向环状流或弹状流的快速转变,对临界热负荷和静力学不稳定性可以带来不利影响。国内外****对泡状流、弹状流和环状流开展了广泛的研究,对其流型转变机理及流动特性都有了丰富的认识。对于气液搅拌流动,液膜振荡剧烈、大波及其失稳产生夹带液滴等是其关键物理过程,由于相关动力学机理与规律缺乏丰富的实验观测与理论分析模型,其流型转变机理仍存在较大争议,是目前认知最少的流型之一,是多相流热物理学基础理论研究中的一个难点科学问题[6],也是研究临界热负荷模型的重要内容[7]。Govan等[8]在下降液膜产生液泛时观察到大波的产生,并在气流的携带下向上运动;Hewitt等[9]对空气-三氯乙烯气液两相搅拌流内大波特性进行了研究,获得了大波波速、频率等实验结果;Barbosa等[10-11]也对空气-水气液两相搅拌流进行了实验研究,获得了大波运动相关实验数据;Parsi等[12]利用网状探针对搅拌流内界面特性进行了研究,获得了相界面分布特征。然而,由于搅拌流流动非常复杂,对搅拌流内大波的运动特性、夹带液滴的产生方式,截面液相分布规律及夹带液滴的粒径大小等关键问题还缺乏系统的认识。
本文针对搅拌流内大波特性进行实验研究,获得了大波波形的数学描述,掌握了不同工况下大波运动的规律。对比分析了气液流量等宏观流动参数对大波的运动特性及其波幅、波长和频率等特征参数的影响规律,提出了用于计算搅拌流内大波平均产生频率的经验关联式。为进一步研究搅拌流内压降特性及液滴夹带奠定了基础。
1 实验 1.1 实验装置 实验系统如图 1所示,主要包括水箱、离心泵、孔板流量计、涡街流量计、数据采集系统、高速摄像系统以及相关的连接管路、阀门和实验段组成。实验段为透明有机玻璃管,内径dT为19 mm,长度为2 m,入水段与抽水段间隔30 mm。为保证进、排水均匀稳定,入水段与抽水段均采用独特蜂窝状结构,即管壁面均匀致密地分布直径约为1 mm的小孔。在实验段顶端设计安装扁嘴型喷嘴,引入旁路气流通过喷嘴产生高速气流将离开实验段的液体吹入出水收集器。采用高速摄像技术捕捉实验段内大波的产生和运动过程。高速摄像系统主要包括日本NAC公司Memrecam fx K3高速摄像机、Nikon公司AF60 mm/2.8D微距镜头、控制计算机和NAC高亮度光纤光源等。
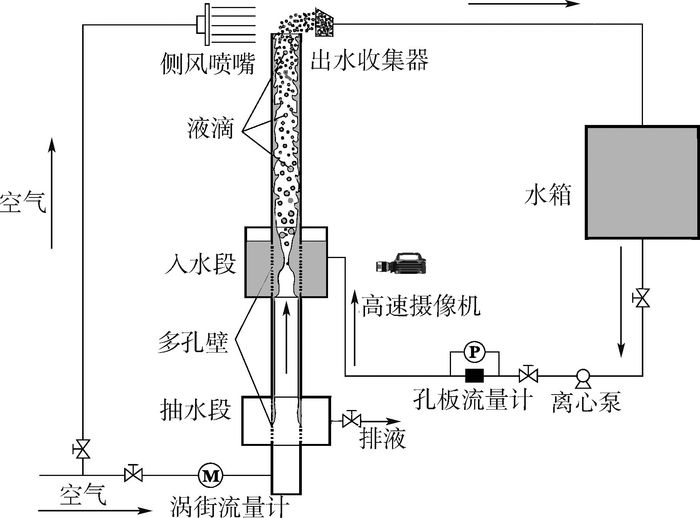 |
| 图 1 实验系统 Fig. 1 Experimental system |
| 图选项 |
1.2 实验方法 弹状流向搅拌流的转变与弹状流内Taylor气泡周围的下降液膜出现液泛现象有着密切的联系[8, 13]。此外,Chaudhry等[14]在液泛实验中发现,当液泛产生时,入水口的上方气液两相流动状态与搅拌流相似。因此本文借鉴液泛的实验方法,获得竖直管内气液两相搅拌流,并将气液界面上出现紊乱的大尺度界面波作为液泛产生的判据[11]。实验过程中,首先稳定较小的气量,缓慢调节出水阀门使液量达到实验值,观察到水从入水孔进入实验段后在重力作用下形成下降液膜。调节连接出水腔阀门,使得下降液膜在流经出水段时被气流抽吸出实验段。下降液膜与气流逆向流动,在气液界面形成界面波并随下降液膜向下运动。逐渐增大气量,当观察到下降液膜在排液孔附近停滞形成大波并在气流的作用下随气流向上运动,认定此时液泛在实验段内产生,随后逐渐增大气量至实验值。本实验在常温、常压下进行, 实验工质为空气-水, 气相流量Qg为5.0~50.0 m3/h, 液相流量Ml为16.29×10-3~40.89×10-3 kg/s。图 2为实验工况点在Hewitt-Roberts流型图[15]上的分布。图中:ρg为气体密度;ρl为液体密度;usg为气速;usl为液速。可以看出,本文所研究的工况点均分布于搅拌流-环状流区域以及靠近弹状流的区域内,这有利于分析搅拌流流动特性与环状流和弹状流的区别。
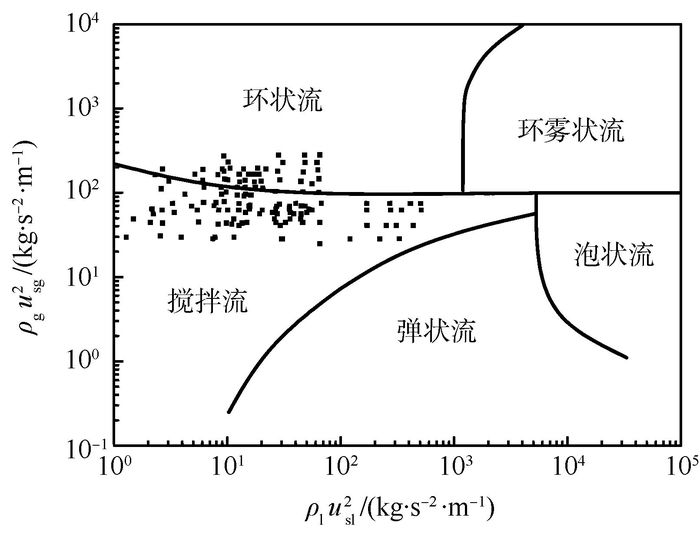 |
| 图 2 实验工况点在Hewitt-Roberts流型图[15]上的分布 Fig. 2 Distribution of experimental operating points on Hewitt-Roberts flow pattern map[15] |
| 图选项 |
1.3 数据处理及误差分析 高速摄像机采集频率为1 000帧/s,采用计数法获得在入水段底端连续产生50个大波所需的时间以计算大波平均产生频率。大波波幅在运动过程中的变化存在2个特殊值:①由于大波在运动过程中存在运动反向,定义大波向下运动停滞时的波幅为临界波幅;②由于在入水段内,进入大波控制体内的液相不断增加,使得大波沿轴向和径向不断发展,当流入大波控制体的液量与流出控制体的液量及夹带剪切产生的液量平衡时,大波波幅达到最大值,定义此时大波波幅为最大波幅。当管径所占像素值已知时,通过比例换算可以获得上述2种情况下大波波幅大小。由于大波在运动过程中受气流剪切力作用产生形变,波峰沿流动方向拉伸,此外,界面波被气流撕裂产生夹带液滴,并使得波峰模糊不清,因此,假设将像素法获得的界面波最大波幅放大1.1倍为最大波幅的真实值。
在实验及数据处理过程中,不可避免地会引入误差,对实验结果产生影响,下面对可能造成的误差进行分析:
1) 水通过孔板流量计进行计量,孔板流量计的不确定度为0.5%,压差采用Rosemount 3051传感器进行测量,不确定度为±0.5%,气相采用涡街流量计进行计量,涡街流量计计量精度等级为1.0。
2) 在实验过程中,当液相流量较大时,大波波幅较大且会对大波上方空气进行压缩,导致局部气相场压力增大,造成小部分气体以气泡形式从入水孔逃逸,由于逃逸产生的气量较小且并不是连续产生,认为可以忽略对实验结果的影响。此外,在排水段也会有部分气体随下降液膜抽吸出实验段,可通过连接出水腔的阀门进行控制,也忽略其对总气量的影响。
3) 在大波波幅数据处理中,由于拍摄速率较高,因此对于反转点判断造成的偏差可以忽略。但由于实验条件的限制,本文通过波幅与管径所占像素比来进行求解,利用较高像素的图片来消除像素法求解波幅的系统误差。本文中所处理的图片像素为300 ppi(pixels per inch,表示每英寸所拥有的像素数量),图片尺寸为950像素(宽)×1 400像素(长)。实验发现,大波在向下运动过程中几乎没有夹带现象产生,而在反转向上运动过程中,由于产生带式破碎或袋式破碎机理,大波被气流撕裂产生夹带液滴,并使得波峰模糊不清。由于大波在临界条件下运动停滞,波形较为固定且无明显形变,因此分析此时的大波波形可以避免较大的误差。
2 实验结果与分析 实验观察到,大波在入水段底端周期性产生并沿管壁运动,在运动过程中破裂形成小液滴。在入水段上方,液膜反复被气流抬升到一定高度后下落并聚集,然后又被气流抬升,使得入水段的上方液膜振荡严重。因此,实验段内存在2个具有明显流动差别的区域,即入水段下方形成较为稳定的下降液膜,与气相场逆向流动;入水段上方液膜振荡严重,气液两相处于搅拌流状态,如图 3所示。
 |
| 图 3 典型搅拌流型特征 Fig. 3 Typical churn flow pattern properties |
| 图选项 |
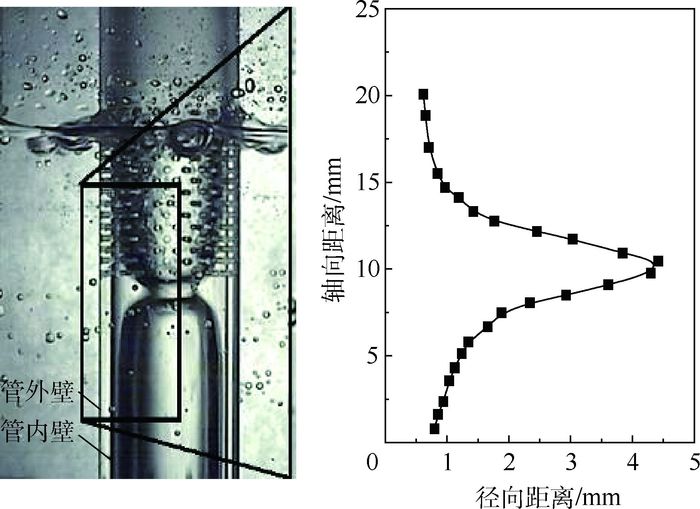
2.1 大波运动特性 大波运动的具体过程如图 4所示。大波在入水段的底端周期性产生,并沿轴向和径向不断发展变化(t=0 ms)。在大波运动初期,由于重力作用大于气相场向上的拖曳力,大波沿着管内壁面向下运动并不断发展,且观察不到夹带现象产生。当大波波幅增长到临界波幅时(液量较大时甚至会出现液桥),大波停止下行并反转向上运动(t=30 ms)。在向上运动过程中,大波持续发展且波峰在气流作用下出现变形,波峰处气液相界面模糊,产生液滴夹带现象(t=50 ms)。当大波运动至入水段上端时,大波几乎完全被气流剪切形成液滴进入气相场,与此同时,新的大波又在入水段底端形成(t=80 ms)。其中,入水段局部大波的运动及变化过程如图 5所示。
 |
| (dT=19 mm, usg=6.17 m/s, usl=7.49×10-2 m/s) 图 4 搅拌流内大波运动发展典型过程 Fig. 4 Typical huge wave behavior in churn flow |
| 图选项 |
 |
| (dT=19 mm, usg=6.17 m/s, usl=7.49×10-2m/s) 图 5 入水段局部大波运动发展过程 Fig. 5 Detailed movement process of huge wave at water inlet |
| 图选项 |
搅拌流内,大波在运动过程中主要受到气相场向上的拖曳力和重力影响,在不同气液流速下,表现出不同的运动特点。图 6揭示了气速对大波运动特性的影响,图中黑线标示大波出现运动反转的位置。结果表明,在一定液相流量条件下,气速越低,作用于大波上的气相场作用力越小,重力对大波的运动影响越大,使得大波沿壁面向下运动的距离越大。当气速增大到接近环状流状态时,气相场作用力完全克服重力的影响,使得大波在入水段底端形成后,立即随气流向上运动。
 |
| (dT=19 mm, Ml=16.25×10-3 kg/s) 图 6 大波下降位置与气速的关系 Fig. 6 Relationship between huge wave reversal position and gas velocity |
| 图选项 |
当气速较高、液速较低时,大波在入水段底端周期性的产生,且由于气相场作用力大于重力的作用,大波在气流作用下保持一定波形向上运动,如图 4所示。当气速较低、液速较高时,大波在入水段内产生的随机性增强,大波及液膜出现明显的扰动,如图 7所示。大波在形成后均在重力作用下沿管壁向下运动,且在运动过程中波形保持稳定。当大波反转向上运动时,波形发生严重扭曲,下降液膜出现剧烈振荡,但随着大波的运动,下降液膜振荡逐渐减弱。当新的大波在入水段内形成时,液膜进入下一个振荡周期。
 |
| (dT=19 mm, usg=4.99 m/s, usl=8.84×10-2 m/s) 图 7 低气速、高液速条件下大波和液膜扰动性 Fig. 7 Huge wave and liquid film perturbation at low gas velocity and high liquid velocity |
| 图选项 |
2.2 大波波形 图 8为对处于临界位置处的大波波形进行提取,通过数学函数拟合,发现大波波形δ(z)符合正态分布函数特性,即
 |
| 图 8 大波波形提取 Fig. 8 Extraction of huge wave's wave shape |
| 图选项 |
 | (1) |
式中:Aw为大波波幅;λ为大波波长;δb为基底液膜厚度。
2.3 大波平均产生频率 图 9为大波平均产生频率f在不同工况下的变化趋势。结果表明,大波平均产生频率随着气速的增加而增加,与环状流内频率变化特性相似。当气速较小时,大波平均产生频率随着液速usl的增加而增加,当气速usg=10.78 m/s时,大波平均产生频率几乎不受液速的影响而趋于定值。
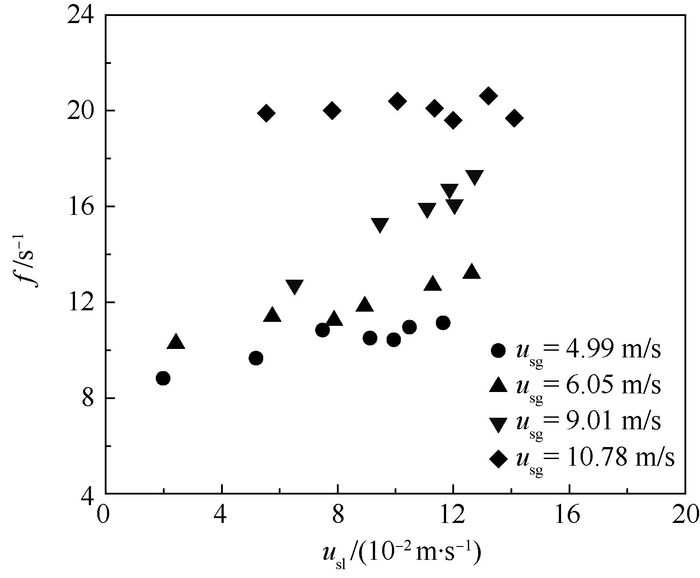 |
| 图 9 大波平均产生频率在不同工况下的变化规律 Fig. 9 Variation rule of average huge wave generation frequency under different working conditions |
| 图选项 |
在气液两相流内,大波平均产生频率f可以用斯特劳哈尔数Sr来进行描述。基于本文实验结果,采用回归分析可以拟合出计算斯特劳哈尔数的经验关联式:
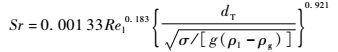 | (2) |
式中:Rel为液相雷诺数;σ为表面张力系数;g为重力加速度。
本文采用Hewitt[9]及Barbosa[10]等的实验结果对式(2)计算精度进行验证,如图 10所示。结果表明,式(2)对Hewitt[9]和Barbosa[10]等实验结果预测精度一般(err=±50%),且相对于Barbosa等[10]实验结果,计算结果明显偏小。除了物性差异外,造成预测精度较低的原因还包括实验段设计及数据处理误差。对于蜂窝型结构,液泛的产生受入水段和出水段之间的距离影响较大,本文实验与Hewitt[9]及Barbosa[10]等入水段和出水段之间的距离分别为0.6、1.2和0.4 m。此外,当气速较低时,实验发现大波在入水段底端并不是均匀产生,因此需要统计大量界面波产生所需要的时间以计算平均值,而三者统计大波数量均有限,因此数据处理也会造成一定的误差。
 |
| 图 10 实验数据验证式(2)计算精度 Fig. 10 Computational accuracy of experimental data verification Eq.(2) |
| 图选项 |
2.4 大波临界波幅 图 11为大波临界波幅Ac在不同气速usg和液相流量Ml下的变化趋势。结果表明,搅拌流内大波波幅比环状流内扰动波波幅大很多(通常环状流内扰动波波幅小于1 mm[16]),但是搅拌流内大波临界波幅变化趋势与环状流内相似,即临界波幅随着气速的增大而减小,随液量的增大而增大并逐渐趋于定值。一方面,这是由于气流剪切力随着气速的增加而不断增大,使得越来越多的液体以夹带液滴的形式离开液膜进入气相场,液膜厚度逐渐减小,使得大波波幅也逐渐减小;另一方面,当液相流量增大时,液膜厚度不断增加,进入大波控制体内的液量也增多,使得大波波幅增加。
 |
| 图 11 大波临界波幅变化规律 Fig. 11 Variation rule of huge wave's critical amplitude |
| 图选项 |
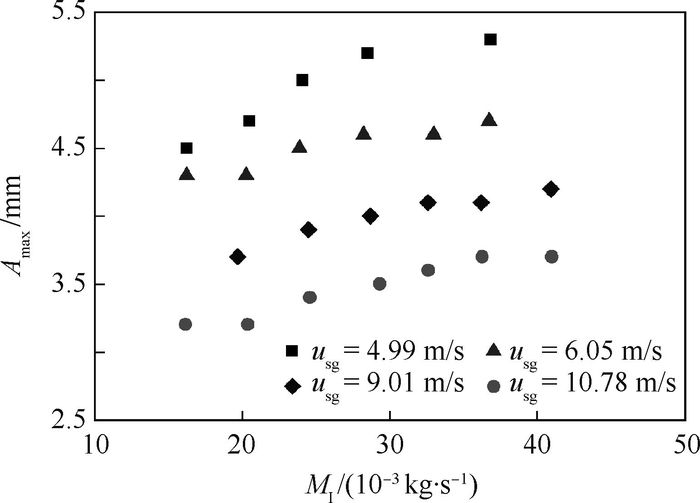
图 12为大波最大波幅Amax在不同气速和液相流量下的变化趋势。与临界波幅相似,最大波幅随着气速的增大而减小,随液量的增大而增大。
 |
| 图 12 大波最大波幅变化规律 Fig. 12 Variation rule of huge wave's maximum amplitude |
| 图选项 |
值得注意的是,由于大波在向上运动过程中,夹带现象的产生对大波波幅的增长产生一定的影响,且气速越大,气流剪切力越大,夹带现象越明显,当进、出控制体的液量平衡时,大波波幅逐渐趋于定值。
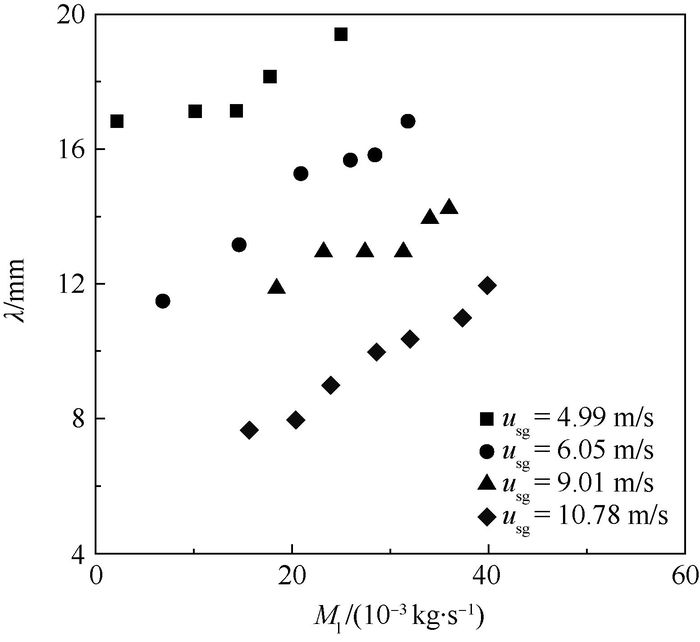
2.5 大波波长 图 13为大波临界位置处的波长在不同工况下的变化趋势。与波幅变化趋势相同,大波波长随着气速的增大而减小,随着液量的增大而增大。
 |
| 图 13 大波波长变化规律 Fig. 13 Variation rule of huge wave's wavelength |
| 图选项 |
3 结论 1) 实验研究发现,搅拌流内液膜流动分为2个不同的区域,即入水段下方形成均匀的下降液膜,入水段上方液相存在显著振荡区域,类似于沸水。大波在相界面处不断形成和发展,并在运动过程中产生夹带液滴。当气速较小时,大波存在运动反向的特征,即大波首先会在重力作用下沿壁面向下运动然后反正向上运动,说明液泛现象是搅拌流内的一个重要特征。
2) 获得了大波波形的正态分布数学描述,分析了流动参数对搅拌流流动特点、大波运动特性、液膜稳定性的影响。结果表明,气液流量对大波波形和液膜稳定性有很大影响,当气相场作用力不足时,大波在运动过程中发生明显的扭曲变形。此外,搅拌流内大波波幅相较于环状流扰动波波幅大。增大气速,大波平均产生频率增加,但波幅和波长减小;增大液速,大波平均产生频率、波幅和波长均增加。
参考文献
| [1] | JAYANTI S, HEWITT G F. Prediction of the slug-to-churn flow transition in vertical two-phase flow[J].International Journal of Multiphase Flow, 1992, 18(6): 847–860.DOI:10.1016/0301-9322(92)90063-M |
| [2] | HEWITT G F. Churn and wispy annular flow regimes in vertical gas-liquid flows[J].Energy & Fuels, 2012, 26(7): 4067–4077. |
| [3] | JAYANTI S, HEWITT G F, JAYANTI S, et al. Prediction of the slug-to-churn flow transition in vertical two-phase flow[J].International Journal of Multiphase Flow, 1992, 18(6): 847–860.DOI:10.1016/0301-9322(92)90063-M |
| [4] | WANG K, BAI B F, MA W M. An improved liquid film model to predict the CHF based on the influence of churn flow[J].Applied Thermal Engineering, 2014, 64(1-2): 422–429.DOI:10.1016/j.applthermaleng.2013.12.064 |
| [5] | NIMWEGEN A T V, PORTELA L M, HENKES R A W M. The effect of surfactants on air-water annular and churn flow in vertical pipes.Part 2:Liquid holdup and pressure gradient dynamics[J].International Journal of Multiphase Flow, 2015, 71: 146–158.DOI:10.1016/j.ijmultiphaseflow.2014.03.007 |
| [6] | TEKAV?I?M, KON?AR B, KLJENAK I. Simulation of flooding waves in vertical churn flow[J].Nuclear Engineering and Design, 2015, 299: 214–224. |
| [7] | 王科, 马江, 白博峰. 气液团状流界内面波运动模型研究[J].工程热物理学报, 2012, 33(12): 2116–2119. WANG K, MA J, BAI B F. Kinematics model and simulation of waves in gas-liquid churn flow[J].Journal of Engineering Thermophysics, 2012, 33(12): 2116–2119.(in Chinese) |
| [8] | GOVAN A H, HEWITT G F, RICHTER H J, et al. Flooding and churn flow in vertical pipes[J].International Journal of Multiphase Flow, 1991, 17(1): 27–44.DOI:10.1016/0301-9322(91)90068-E |
| [9] | HEWITT G F, MARTIN C, WILKES N. Experimental and modelling studies of annular flow in the region between flow reversal and the pressure drop minimum[J].Physicochemical Hydrodynamics, 1985, 6(1): 69–86. |
| [10] | BARBOSA J R, GOVAN A H, HEWITT G F. Visualisation and modelling studies of churn flow in a vertical pipe[J].International Journal of Multiphase Flow, 2001, 27(12): 2105–2127.DOI:10.1016/S0301-9322(01)00048-9 |
| [11] | BARBOSA J R, HEWITT G F, K?NIG G, et al. Liquid entrainment, droplet concentration and pressure gradient at the onset of annular flow in a vertical pipe[J].International Journal of Multiphase Flow, 2002, 28(6): 943–961.DOI:10.1016/S0301-9322(02)00003-4 |
| [12] | PARSI M, VIEIRA R E, TORRES C F, et al. Experimental investigation of interfacial structures within churn flow using a dual wire-mesh sensor[J].International Journal of Multiphase Flow, 2015, 73: 155–170.DOI:10.1016/j.ijmultiphaseflow.2015.03.019 |
| [13] | HEWITT G F, JAYANTI S. To churn or not to churn[J].International Journal of Multiphase Flow, 1993, 19(3): 527–529.DOI:10.1016/0301-9322(93)90065-3 |
| [14] | CHAUDHRY A, EMERTON A, JACKSON R.Flow regimes in the co-current upwards flow of water and air[C]//Symposium on Two-phase Flow, 1965:B2. |
| [15] | HEWITT G F, ROBERTS D.Studies of two-phase flow patterns by simultaneous X-ray and flash photography:AERE-M2159[R].Harwell:UKAEA Report, 1969. |
| [16] | SAWANT P, ISHⅡ M, HAZUKU T, et al. Properties of disturbance waves in vertical annular two-phase flow[J].Nuclear Engineering and Design, 2008, 238(12): 3528–3541.DOI:10.1016/j.nucengdes.2008.06.013 |
