目前绳牵引并联机构(WDPR)支撑方式主要应用于低速风洞试验,如文献[5]已经将绳牵引支撑方式应用于FL-8闭口式风洞;法国国家航空研究局支持的“SACSO项目”已经成功将绳牵引支撑方式应用于立式风洞测力试验[6-7]。文献[8-9]构建了一套8根绳牵引的六自由度支撑机构,通过内置六分量天平,在低速风洞试验中得到成功应用,获得了飞行器模型的气动参数。而目前绳牵引并联支撑在高速、高超声速中应用的研究还比较少,文献[10]主要研究了高速风洞弹体张线支撑的干扰,并进行试验验证,但其原理上不同于绳牵引并联支撑。国外也有相关研究将张线支撑应用于高超声速风洞试验。文献[11]构建了一套柔性悬挂系统加尾撑的装置,采用4根细杆前后分布于机身,将其悬挂吊起,应用于X-51模型的高超声速风洞试验,并测得了模型升阻力。文献[12]以X-51A模型为例,分析了绳牵引并联支撑系统的稳定性,绳系张力的变化以及气动力解算方法,但对支撑干扰只进行了初步的研究。
综上所述,为进一步研究绳牵引并联支撑在高超声速风洞试验中应用的可行性,有必要继续分析绳牵引并联支撑系统的稳定性与气动干扰等问题。
本文以10°尖锥标准模型[13-14]为例,首先设计了应用于高超声速风洞的绳牵引并联支撑机构,包括在试验段中的布局,牵引绳的布置等,建立三维模型。针对绳牵引并联支撑系统进行了稳定性分析,以及参数优化。然后,采用CFD数值计算软件,分别对有/无绳牵引并联支撑的情况进行气动仿真与分析。最后,研究绳牵引并联支撑的刚度,分析低阶固有频率以及振型,并与弯刀支撑情况做比较。本文的研究结果可以为绳牵引并联支撑在高超声速风洞试验中的应用提供参考,从而在某些使用传统硬式支撑测试困难的情况下,能够采用绳牵引并联支撑这种新的方式进行有效的补充和验证。
1 绳牵引并联支撑系统设计 由于绳索单向受力的特点,绳牵引并联机构通常采取冗余驱动,即n自由度绳牵引并联机构至少需由n+1根绳牵引;如果少于等于n根绳,就需要外力(或重力)来保持稳定性[15]。为实现模型六自由度运动,本文设计了8根牵引绳,以尖锥标模为研究对象,其半锥角为10°,长度为2 m。绳牵引并联支撑系统在风洞试验段的设计和锥体模型在试验段的安装情况如图 1所示。将锥体模型置于试验段中部观察窗的可视范围之内。从模型上的牵引点处引出牵引绳,牵引绳分别经过内室上、下壁的滑轮与驻室壁上的驱动装置连接,通过控制驱动装置,以控制绳长的变化从而实现控制模型姿态的变化。位于内室上壁处安装有相机,模型上布置有若干感光标志点,当模型运动时,相机通过识别模型上标志点的位置,采集模型的位姿。
 |
| 1—驻室前壁;2—试验段入口;3—驻室左壁;4—驻室上壁;5—滑轮;6—相机;7—内室上壁;8—驻室后壁;9—锥体模型;10—驻室右壁;11—观察窗;12—内室右壁;13—内室下壁;14—驻室下壁;15—滚轴丝杠和电机。 图 1 模型在风洞中安装示意图 Fig. 1 Schematic of model installation in wind tunnel |
| 图选项 |
绳牵引并联支撑系统原理样机如图 2所示。考虑到系统的刚度与稳定性,锥体模型由8根钢丝绳支撑起来,悬挂在空中。通过工控机控制8个伺服电机带动滑块运动,实现牵引绳长度的调节,以满足风洞试验对模型不同位姿的调整,实现锥体模型的六自由度运动。
 |
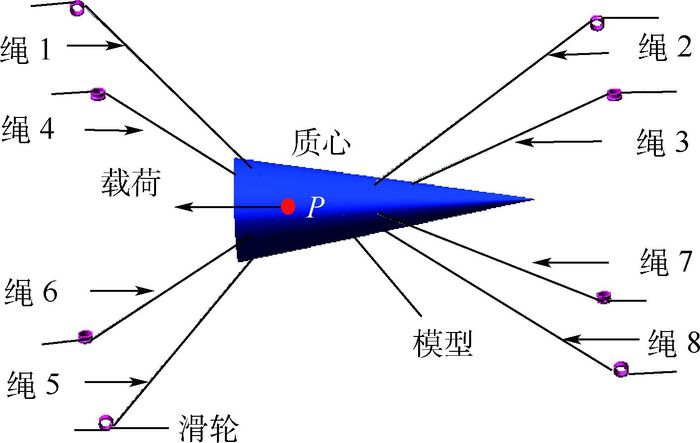
| P—模型质心;Pi—绳与模型的连接点,i=1~8;Bi—绳与固定滑轮的连接点;Pxyz—本体坐标系;OXYZ—惯性参考坐标系。 图 2 原理样机 Fig. 2 Principle prototype |
| 图选项 |
锥体模型上分别有8个牵引点P1~P8,牵引绳系分别与之连接,然后通过各自对应的万向滑轮(B1~B8)变向,之后分别与各自对应的滚轴丝杠上的滑块相连。设定惯性参考坐标系OXYZ与模型初始零位姿状态保持一致。结合系统的刚度[16],Pi和Bi点的布局如表 1所示。
表 1 绳连接点Pi和Bi的坐标 Table 1 Coordinates of wire attachment points Pi and Bi
| Pi点坐标/mm | Bi点坐标/mm |
| P1=(-438.2,241.7,241.7) | B1=(-1 509,1 145,1 145) |
| P2=(400.7,194.8,112.2) | B2=(1 940,955,955) |
| P3=(400.7,194.8,-112.2) | B3=(1 940,955,-955) |
| P4=(-438.2,241.7,-241.7) | B4=(-1 509,1 145,-1 145) |
| P5=(-438.2,-2 41.7,-241.7) | B5=(-1 509,-1 145,-1 145) |
| P6=(-438.2,-241.7,241.7) | B6=(-1 509,-1 145,1 145) |
| P7=(400.7,-194.8,112.2) | B7=(1 940,-955,955) |
| P8=(400.7,-194.8,-112.2) | B8=(1 940,-955,-955) |
表选项
2 绳牵引并联支撑系统稳定性 为研究绳牵引并联支撑系统应用于高超声速风洞试验的可行性,本节重点分析气动载荷作用下系统的稳定性,并优化绳直径参数。采用ADAMS动力学仿真软件对系统进行建模,图 3为绳牵引支撑系统,其中锥体模型质量为80 kg。
 |
| 图 3 绳牵引并联支撑锥体模型 Fig. 3 Wire-driven parallel support cone model |
| 图选项 |
为考察不同绳直径对系统稳定性的影响,分别选择直径为4、5、6 mm进行仿真分析。初始状态下8根牵引绳所受预紧力设置为F=(1 257, 1 772, 2 251, 1 266, 2 032, 2 003, 2 428, 1 905)N,其次在模型质心处施加相应的力用以模拟模型在流场中受到的气动载荷。如0°迎角时,锥体模型所受阻力为

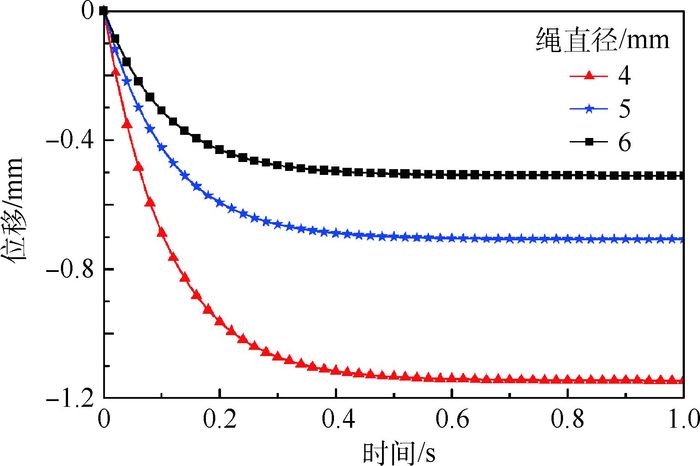 |
| 图 4 模型质心位移的变化 Fig. 4 Change of displacement of model's center of mass |
| 图选项 |
由图可知,在冲击力作用下模型质心位置发生变化,经过0.4 s后处于稳定状态。绳直径为4 mm时,模型质心位移1.15 mm;绳直径为5 mm时,模型质心位移0.71 mm;绳直径为6 mm时,模型质心位移0.51 mm。这3种状态下模型质心位移基本处于毫米级,质心位置变化较小。
模型受冲击力作用后各根绳所受拉力发生变化,为优化绳直径参数,这里主要关注拉力最大的绳。表 2为不同直径的绳拉力最大值,以及绳能承受的拉力极限值。
表 2 不同直径钢丝绳受力 Table 2 Force on steel wire ropes with different diameters
| 绳直径/mm | 绳拉力最大值/kN | 绳能承受的拉力极限值/kN |
| 4 | 2.79 | 8 |
| 5 | 2.80 | 12 |
| 6 | 2.80 | 18 |
表选项
由表 2可知,3种不同直径钢丝绳受冲击载荷作用时绳所受的最大拉力差别较小,基本都在2.80 kN左右。因此,从钢丝绳所能承受的拉力考虑,以上3种情况均能满足使用性能。综合考虑质心位移,以及满足使用性能情况下,本文选取绳直径为5 mm的钢丝绳。
第3节将重点分析牵引绳引起的气动干扰。
3 气动力计算 3.1 控制方程 高超声速流动情况比较复杂,涉及边界层,激波,各种化学反应等复杂物理化学现象,数值模拟所有情况比较复杂且难以做到精确计算。本文忽略高温气体效应及化学反应等情况。采用无量纲化三维可压Navier-Stokes方程做为流动控制方程:
 | (1) |
式中:Q为守恒变量;Fk为对流通量;Fv, k为黏性通量。Navier-Stokes方程采用空间离散方式,对流项采用FDS-Roe格式离散,黏性项采用二阶中心差分格式。
3.2 网格生成 本文使用商用软件ANSYS ICEM进行网格划分,采用代数生成法生成结构网格。为节省计算资源,采用SYM对称面,计算半模。锥体长为2 m,半锥角为10°,底部直径为0.704 m,绳直径为5 mm,有绳状态下模型的绳长为1 m。计算域采用矩形计算域,长×宽×高分别为9 m×3 m×2 m。锥体表面生成外O-block,对锥体表面进行加密。设置边界层数为25层,第1层网格高度为2×10-6 m。绳表面同样生成外O-block,对绳周围网格进行加密,设置边界层数为25层,第1层网格高度设置为0.5×10-6 m。无绳系支撑锥体模型网格总量为400万左右,有绳系支撑锥体模型网格总量为600万左右。如图 5为绳牵引并联支撑系统流场网格分布情况。
 |
| 图 5 绳牵引并联支撑系统流场网格分布 Fig. 5 Grid distribution of flow field with wire-driven parallel support system |
| 图选项 |
4 数值模拟结果与分析 为研究绳系支撑方式在高超声速风洞试验中应用时支撑的气动力干扰问题,本文数值计算主要借助FLUENT软件求解Navier-Stokes方程。采用定常计算,湍流模型选用两方程k-ω SST模型。来流马赫数为7.8,来流静压为2 071.3 Pa,来流温度为236.5 K。以底部直径为参考长度的雷诺数为1.12×108。边界条件设置,由于来流可压且速度较高,故进出口均选择压力远场边界条件。锥体物面为无滑移壁面条件,求解器的设置采用基于密度基的隐式耦合求解。
4.1 气动力系数 分别计算了迎角0°~8°下有绳牵引支撑和无绳支撑法向力系数(CN)以及轴向力系数(CA),并将本文模拟结果的法向力系数与CAS试验结果[16]进行了比较分析,其中CAS试验采用的是传统硬式支撑方式。
有绳支撑和无绳支撑状态下法向力系数与试验数据[16]对比如表 3和图 6所示,α为迎角。计算结果表明,随着迎角增大,流场对模型产生向上的升力,法向力系数几乎呈线性增长,整体而言数值计算的法向力系数变化规律和文献[16]的试验数据基本一致,绳系支撑状态下数值计算结果和试验数据相比各个角度下法向力系数均比试验数值大,整体平均状态下相对试验误差为4%,绳系支撑状态下数值计算结果和试验数据相比,一定程度上证明了数值计算的可靠性。数值计算的有绳和无绳状态下法向力系数的对比,无绳状态下法向力系数比有绳状态下偏高,最大相对误差为3.4%,由此可见绳系支撑对法向力系数影响较小。
表 3 法向力系数计算结果与试验结果对比 Table 3 Comparison of normal force coefficient between calculation results and test results
| 迎角/(°) | 法向力系数 | ||
| 无绳支撑 | 有绳支撑 | 试验[16] | |
| 0 | 0 | 0 | 0 |
| 2 | 0.075 7 | 0.073 6 | 0.067 5 |
| 4 | 0.151 6 | 0.146 3 | 0.140 6 |
| 6 | 0.227 5 | 0.220 3 | 0.212 9 |
| 8 | 0.305 4 | 0.295 4 | 0.283 8 |
表选项
 |
| 图 6 法向力系数 Fig. 6 Normal force coefficient |
| 图选项 |
由于弯刀支撑方式对轴向力试验数据影响较大,故图 7仅显示有绳支撑和无绳支撑状态下轴向力系数仿真结果。在迎角0°~4°状态下时,轴向力系数大小受迎角变化影响小。迎角大于4°时,轴向力系数受迎角变化影响明显,角度增大,轴向力系数变大。整体而言,各个迎角下有绳系支撑比无绳系状态下轴向力系数大,最大相对误差为6.3%。
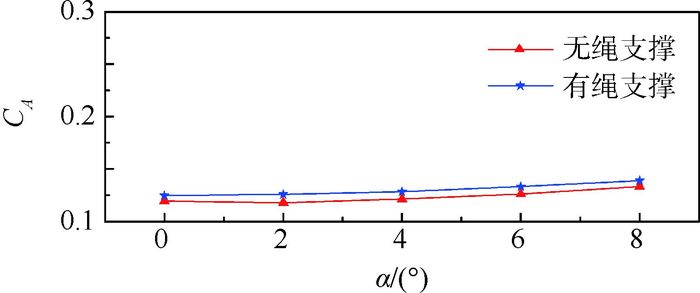 |
| 图 7 轴向力系数 Fig. 7 Axial force coefficients |
| 图选项 |
图 8为有绳支撑和无绳支撑状态下锥体表面摩阻系数(Cf)随迎角变化情况。迎角的变化对锥体模型表面摩阻系数影响相对较小,主要因为摩擦力是切向速度在法向的梯度,对迎风面和背风面这种区域性的影响较小。有绳系支撑比无绳支撑状态下摩阻系数相对高一些,随迎角增加的变化趋势基本一致。
 |
| 图 8 摩阻系数 Fig. 8 Coefficients of friction resistance |
| 图选项 |
图 9为摩阻比值(摩擦阻力(Ff)与总阻力(FD)的比值)随迎角变化情况。随着迎角变大,摩阻比逐渐下降。这一现象主要是因为随着锥体模型迎角变大,其迎风面积增大,导致阻力变化较大;由于迎角对摩阻影响较小,所以随着迎角增大,摩阻比呈现变小的趋势。因此在大迎角下阻力主要来自于波阻。
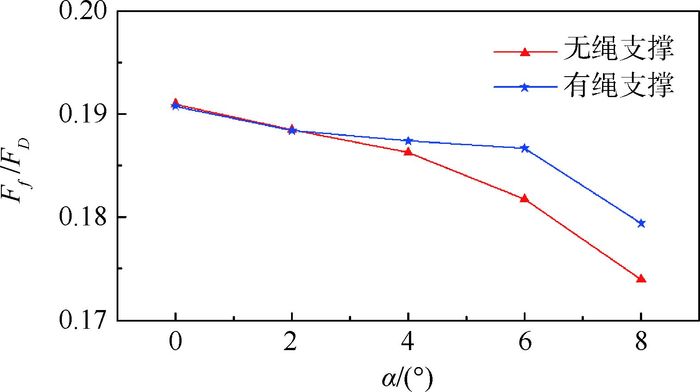 |
| 图 9 摩阻比值 Fig. 9 Ratio of friction to drag |
| 图选项 |
4.2 压力分布 如图 10所示为0°迎角时,有绳支撑和无绳支撑状态下锥体表面压力分布。在锥体头部位置有斜激波产生,绳系对锥体周围流场的影响范围较小,只对其下游流场产生局部影响。
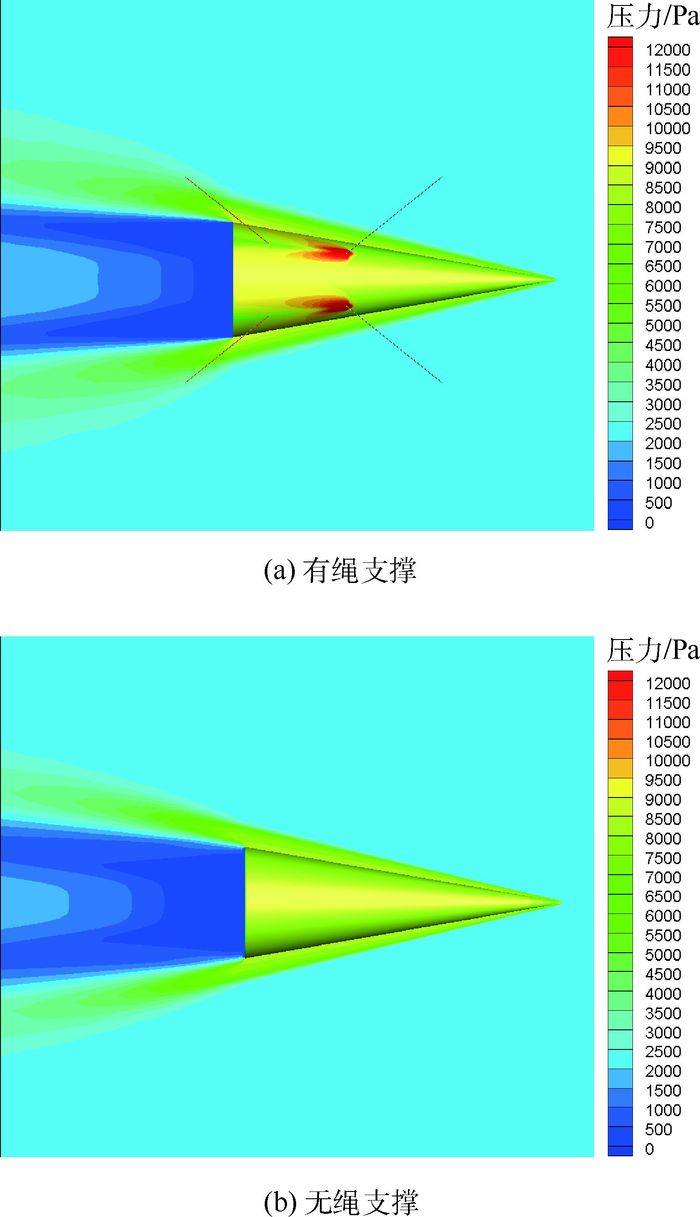 |
| 图 10 迎角为0°时压力分布 Fig. 10 Pressure distribution at 0° angle of attack |
| 图选项 |
如图 11所示,绳牵引状态下迎角为2°和8°时锥体周围压力分布图。由于迎角的变大,锥体模型上表面压力分布变化越来越不明显,即上表面斜激波随着迎角的增大而减弱。下表面为迎风面比上表面背风面压力变化明显,说明迎风面激波更强。模型下表面激波与模型壁面夹角随着迎角的增大而减小。迎风面绳周围风压比背风面绳周围风压变化更明显。
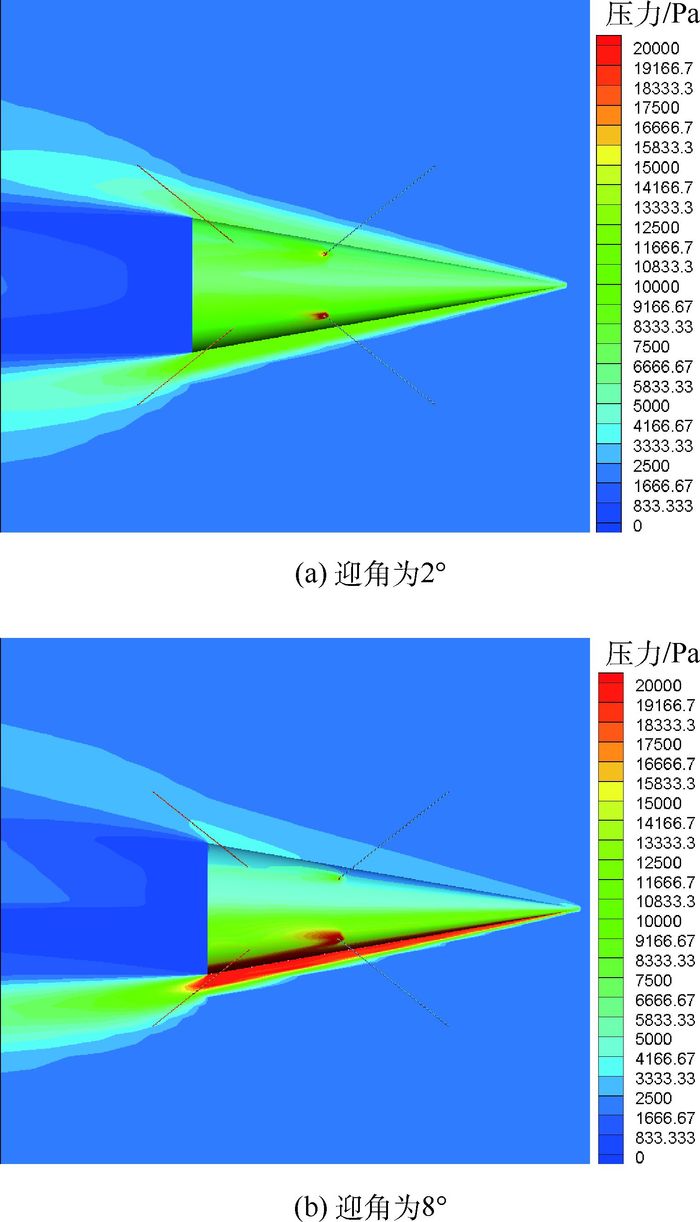 |
| 图 11 有绳支撑下迎角为2°和8°时压力分布 Fig. 11 Pressure distribution with support at 2° and 8° angles of attack |
| 图选项 |
单绳周围压力分布如图 12所示,绳的前缘迎风面压力急剧上升形成一道弓形激波,随后激波逐渐减弱变成马赫波。在绳的背风面形成一个小范围的低压区,随后压力有所增大。整体而言,绳对其下游流场的影响范围约是其直径的10倍。
 |
| 图 12 单绳周围压力分布 Fig. 12 Pressure distribution around single rope |
| 图选项 |
迎角为0°绳系周围流场压力分布情况如图 13所示,其为距离对称面高度0.33 m处的一个流场截面图。绳的迎风面有弓形激波产生,随后膨胀消失。绳系对其周围流场压力分布有一定影响,但影响范围较小,主要影响其下游流场分布。上游绳系之间由于相隔距离较大,绳对流场的影响范围较小,因此,流场不会相互干扰。
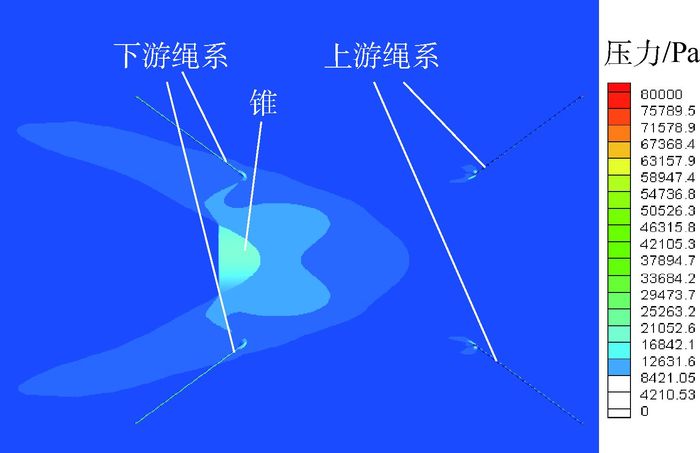 |
| 图 13 迎角为0°绳系周围压力分布 Fig. 13 Pressure distribution around ropes at 0° angle of attack |
| 图选项 |
5 系统模态分析 为进一步探索研究绳牵引并联支撑系统应用于高超声速风洞试验的可行性,本文对其支撑模态进行了仿真分析,并对比了传统硬式支撑的情况。
5.1 绳牵引并联支撑系统模态分析 研究绳牵引并联支撑系统模态本文主要借助ADAMS软件中的Vibration模块,进行固有频率分析。模态分析时,分别对8根绳施加预紧力,采用频域算法,最后得到系统锥体零姿态状态下的前六阶固有频率情况,如表 4所示。
表 4 绳牵引并联支撑系统模态分析 Table 4 Wire-driven parallel support system modal analysis
| 阶数 | 频率/Hz | 振型 |
| 一阶 | 7.26 | 偏航 |
| 二阶 | 15.43 | 俯仰 |
| 三阶 | 22.14 | 滚转 |
| 四阶 | 34.93 | X轴向 |
| 五阶 | 39.90 | Z轴向 |
| 六阶 | 40.07 | Y轴向 |
表选项
由表 4可知,支撑系统前六阶未出现模态密集现象,并且各阶模态之间有一定程度上的分离,有助于系统固有频率的调整[18]。
系统模态分析中各阶模态振型未出现明显的耦合现象。一阶固有频率为7.26 Hz,振型主要表现为偏航方向。仿真结果中偏航方向刚度相对较小,而风洞试验中飞行器模型主要受轴向力作用,因此对偏航这个方向上的振动影响会比较小。
5.2 硬式支撑模态分析 采用硬式支撑状态下的锥体模型如图 14所示。
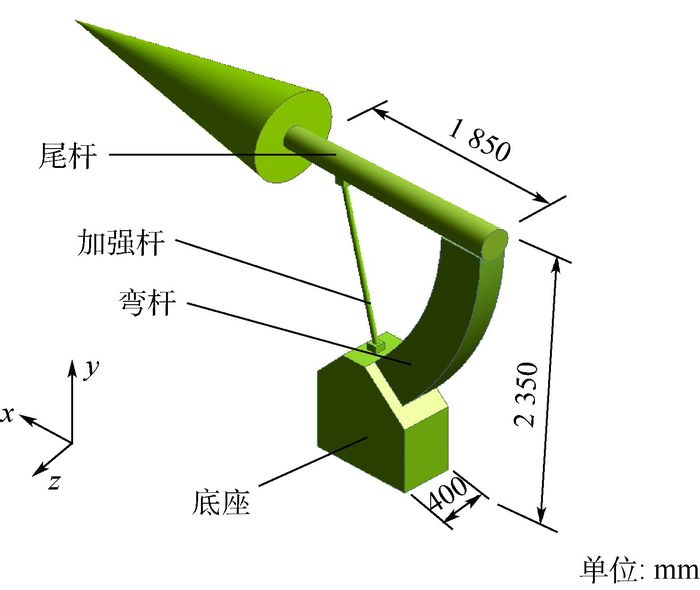 |
| 图 14 硬式支撑模型 Fig. 14 Hard support model |
| 图选项 |
本文中对比的锥体的硬式支撑方式是尾撑,此硬式支撑主要由4部分组成,分别是底座、弯杆、尾杆、加强杆。尾杆的设计在与模型连接处较细,以尽量减小对模型外形的破坏。由于弯刀支撑是悬臂梁的设计,为加强其结构稳定性,设计有加强杆。整个尾撑机构基本尺寸长×宽×高为1 850 mm×400 mm×2 350 mm,采用钢材料。
对硬式支撑状态下整体模态分析主要借助商用软件workbench中的modal模块,得出该支撑状态下整体前六阶固有频率如表 5所示。
表 5 硬式支撑模态分析 Table 5 Hard support modal analysis
| 阶数 | 频率/Hz | 振型 |
| 一阶 | 1.25 | 俯仰 |
| 二阶 | 1.49 | 偏航 |
| 三阶 | 1.78 | 偏航 |
| 四阶 | 5.59 | 俯仰/轴向(x) |
| 五阶 | 26.34 | 滚转 |
| 六阶 | 92.92 | 竖向(y) |
表选项
硬式支撑前三阶固有频率都比较低,分别为1.25、1.49、1.78 Hz并且模态比较密集,容易出现振动相互耦合影响。一阶固有频率为1.25 Hz,振型表现为俯仰方向,主要因为硬式支撑为了减少支撑对气流的干扰将与模型接触的终端设计成细长悬臂梁的结构,导致俯仰方向强度比较弱。二、三阶同样固有频率较低,振型都表现为偏航方向。二阶振型主要为锥体头部偏航,三阶主要是锥体底部以及与其相连的连接杆的偏航。四阶模型振动有耦合现象。
对比2种支撑方式的模态分析结果,相比硬式支撑方式,绳牵引并联支撑系统前几阶频率比较高,因此刚度更好,而且未出现模态密集的现象,模态之间有一定程度的分离,相互之间耦合较小。
6 结论 本文针对绳并联支撑系统在高超声速风洞试验中的应用可行性进行了分析,主要结论如下:
1) 高超声速气流冲击作用下,支撑系统是稳定的,模型质心的变化为毫米量级,绳拉力变化也满足强度要求。
2) 有绳支撑和无绳支撑状态下模型,其气动力系数(法向力系数和轴向力系数)变化规律基本一致。法向力系数最大相对误差为3.4%,轴向力系数最大相对误差为6.3%。将数值计算的有绳牵引并联支撑锥体模型法向力系数与文献试验数据对比,结果法向力系数随迎角变化规律基本一致。法向力系数平均相对误差为4%,证明了计算结果的可靠性。
3) 与弯刀支撑机构相比,绳牵引并联支撑锥体模型的固有频率较高,系统的刚度更大,有利于提高试验系统的稳定性。
综上所述,在高超声速风洞中采用绳牵引并联支撑机构,不仅能够实现模型的动态调整,而且产生的气动干扰相对较小,支撑刚度较大,可以为高超声速飞行器的风洞试验支撑技术提供理论依据和指导。
参考文献
| [1] | CYRAN B.Sting interference effects on the static, dynamic and base pressure measurements of the standard dynamics model aircraft at Mach number 0.3 through 1.3:AEDC-TR-81-3[R].Tennessee:AEDC, 1981. |
| [2] | 章荣平, 王勋年, 李真旭, 等. 低速风洞尾撑支杆干扰研究[J].实验流体力学, 2006, 20(3): 33–38. ZHANG R P, WANG X N, LI Z X, et al. Investigation of sting support interference in low speed wind tunnel[J].Journal of Experiments in Fluid Mechanics, 2006, 20(3): 33–38.(in Chinese) |
| [3] | SHAN G H.Wind tunnel investigation of aerodynamic and tail buffet characteristics of leading-edge extension modifications to the F/A-18:AIAA-1991-2889[R].Reston:AIAA, 1991. |
| [4] | 刘雄伟, 郑亚青, 林麒. 应用于飞行器风洞试验的绳牵引并联机构技术综述[J].航空学报, 2004, 25(4): 393–400. LIU X W, ZHENG Y Q, LIN Q. Overview of wire-driven parallel kinematic manipulators for aircraft wind tunnels[J].Acta Aeronautica et Sinica, 2004, 25(4): 393–400.(in Chinese) |
| [5] | 卞於中, 李祥瑞, 李立, 等. 低速闭口风洞模型张线支撑及内天平测量系统的研制[J].流体力学实验与测量, 1999, 13(3): 85–90. BIAN Y Z, LI X R, LI L, et al. Development of model cable mount and strain gauge balance measuring system in low speed closed wind tunnel[J].Experiments and Measurements in Fluid Mechanics, 1999, 13(3): 85–90.(in Chinese) |
| [6] | LAFOURCADE P, LLIBRE M, REBOULET C.Design of a parallel wire-driven manipulator for wind tunnels[C]//Proceedings of the Workshop on Fundamental Issues and Future Directions for Parallel Mechanisms and Manipulators.Berlin:Springer, 2002:187-194. |
| [7] | LAFOURCADE P.Study of parallel cable manipulators and design of an active suspension for wind tunnel[D].Malakoff Cedex:ENSAE, 2004. |
| [8] | XIAO Y W, LIN Q, ZHENG Y Q, et al. Model aerodynamic tests with a wire-driven parallel suspension system in low-speed wind tunnel[J].Chinese Journal of Aeronautics, 2010, 23(4): 393–400.DOI:10.1016/S1000-9361(09)60233-8 |
| [9] | 郑亚青, 林麒, 刘雄伟, 等. 用于低速风洞飞行器气动导数试验的绳牵引并联支撑系统[J].航空学报, 2009, 30(8): 1549–1554. ZHENG Y Q, LIN Q, LIU X W, et al. On wire-driven parallel suspension systems for static and dynamic derivatives of aircraft in low-speed wind tunnels[J].Acta Aeronautica et Sinica, 2009, 30(8): 1549–1554.(in Chinese) |
| [10] | 于卫青, 刘高计, 李通, 等. 弹箭模型高速风洞张线支撑干扰试验方案研究[J].弹箭与制导学报, 2014, 34(5): 144–147. YU W Q, LIU G J, LI T, et al. Research on the missiles hanging brace interference test in high-speed wind tunnel[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(5): 144–147.(in Chinese) |
| [11] | MICHAEL H, TIMOTHY W, MATTHEW M, et al.A review of basic research and development programs conducted in the LENS facilities in hypervelocity flows[C]//50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition.Reston:AIAA, 2012:1-17. |
| [12] | WANG X, PENG M, HU Z, et al. Feasibility investigation of large-scale model suspended by cable-driven parallel robot in hypersonic wind tunnel test[J].Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2017, 231(13): 2375–2383.DOI:10.1177/0954410016662067 |
| [13] | ERICSSON L E, REDING J R. Review of support interference in dynamic tests[J].AIAA Journal, 1983, 21(12): 1652–1666.DOI:10.2514/3.60166 |
| [14] | 马家驩, 潘文欣, 翟曼玲, 等. 10°尖锥标模高超声速动导数的实验测量[J].空气动力学学报, 1997, 15(4): 452–457. MA J H, PAN W X, ZHAI M L, et al. 10° cone model free flight experiment in hypersonic impulse type wind tunnel for dynamic stability measurement[J].Acta Aerodynamica Sinica, 1997, 15(4): 452–457.(in Chinese) |
| [15] | MING A, HIGUCHI T. Study on multiple degree of freedom positioning mechanisms using wires (Part 1):Concept, design and control[J].International Journal of the Japan Society for Precision Engineering, 1994, 28(2): 131–138. |
| [16] | WANG X G, MA S Y, LIN Q.Hybrid pose/tension control based on stiffness optimization of cable-driven parallel mechanism in wind tunnel test[C]//IEEE International Conference on Control, Automation and Robotics.Piscataway, NJ:IEEE Press, 2016:75-79. |
| [17] | 杨耀栋, 王复, 郭大华. 10°尖锥模型的气动力测量[J].实验流体力学, 1988(1): 60–64. YANG Y D, WANG F, GUO D H. Aerodynamic force measurement of 10° cone model[J].Journal of Experiments in Fluid Mechanics, 1988(1): 60–64.(in Chinese) |
| [18] | 陈万华, 王超琪, 谢国栋, 等. FL-26风洞模型支撑系统动态仿真分析[J].中国机械工程, 2012, 23(2): 161–166. CHEN W H, WANG C Q, XIE G D, et al. Dynamic simulation analysis of model support system in FL-26 wind tunnel[J].China Mechanical Engineering, 2012, 23(2): 161–166.(in Chinese) |
