昆虫是自然界中体积最小、机动能力最好的飞行者，它们可以悬停、跃升、前飞、上下飞、倒飞和侧飞等，对其飞行机理的清楚认识不仅有利于生物学家分析昆虫的形态结构、生理特点以及其飞行方式对进化的影响，还可以为工程专家提供研制飞行器的生物模型基础。近年来，人们通过实验和数值计算手段对昆虫飞行过程中高升力的产生机理进行了研究，但研究中主要是针对其悬停、前飞和上下飞^[1-8]等飞行状态，而侧飞作为昆虫飞行状态的一种，其气动特性相对悬停的变化仍不清楚；另外，昆虫在自然界中飞行时多会受到侧风的干扰，这种侧向来流对其拍动翅的气动特性是否会产生影响，影响又会有多大？对于这些问题的清楚认识也将为扑翼微型飞行器的研制提供一定的空气动力学基础。
本文以蜂蝇翅膀为模型，运用数值模拟的方法计算了存在侧风时拍动翅上的气动力，并与无侧风的正常悬停情况进行对比，从侧风的方向和强度2个方面考察其对拍动翅气动特性的影响。
1 方法 1.1 翅膀模型及运动 本文拍动翅模型基于蜂蝇翅膀，其平面形状取自文献[9]，如图 1(a)所示。模型翅剖面形状如图 1(b)所示。平板厚度为3%c(c为翅膀平均弦长)，前后缘为半径是0.5%c的圆弧。模型翅面积二阶矩折合半径r₂为0.55R(R为翅膀长度)。

图 1 蜂蝇模型翅平面图[9]及剖面图 Fig. 1 Planform[9] and sectional view of model dronefly wing

图选项

为方便描述拍动翅的运动，首先引入右手坐标系O₁x₁y₁z₁：坐标原点O₁位于翅根，平面x₁y₁与翅膀拍动平面重合，如图 2所示。根据实验观测^[10]，模型翅的拍动运动由2个部分组成：①绕z₁轴的转动，转角记为?，称为拍动角；②绕翅膀展向轴的转动，转角记为α，称为攻角。

图 2 模型翅运动及坐标系示意图 Fig. 2 Schematic of reference frames of wing motion

图选项

翅膀的拍动角?随时间变化的规律近似为简单的三角函数：

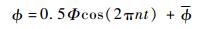(1)

式中：Φ为翅膀拍动幅角；n为拍动频率；?为拍动平均角。令?_min和?_max分别代表翅膀的最小和最大拍动角(见图 2(c)，v为侧风的速度)，则Φ=?_max-?_min，?=(?_min+?_max)/2。
翅膀的拍动攻角α在下拍和上拍中部近似为常数(下拍中部常数记作α_d，上拍中部常数记作α_u)；翻转过程中，攻角随时间的变化规律可看作简单的谐波函数。以翅膀在第k个周期的上仰运动为例，攻角随时间的变化表示如下：

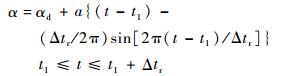(2)

式中：a为常数；t₁为翅膀开始反转的时刻；Δt_r为翅膀的翻转时间。

(3)

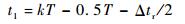(4)

其中：T为翅膀拍动周期。
翅膀的下翻运动也可采用同样的方式描述。如图 1所示，带有圆点的直线表示模型昆虫翅膀翻转转轴的位置。从式(1)~式(4)可以看出，为描述翅膀的拍动运动，需要给出以下运动参数：Φ、n、Δt_r、α_d、α_u和?。为描述拍动平面，还需确定拍动平面倾角β。将式(1)和式(2)利用参考速度U、参考长度c和参考时间c/U无量纲化后(U为r₂处的平均线速度，定义为U=2Φnr₂)，可知，只需给出Φ、α_d、α_u、?和Δt_r^*(Δt_r^*为无量纲化后的翻转时间，Δt_r^*=Δt_rU/c)，即可确定模型翅的运动模式。
1.2 Navier-Stokes方程及计算方法 在惯性坐标系Oxyz下，非定常不可压缩Navier-Stokes方程无量纲形式可表示为

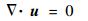(5)

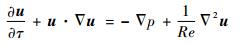(6)

式中：u为无量纲速度；p为无量纲压力；τ为无量纲时间；?为梯度算子；?²为拉普拉斯算子；Re为雷诺数(定义为Re=Uc/ν，ν为运动黏性系数)。
Navier-Stokes方程的数值解法与文献[3]相同，采用Rogers等^[11]发展的拟压缩方法概述如下：在连续性方程中加入压力对拟时间的偏导数，物理上将不可压缩流看作可压缩流；动量方程中，速度的时间导数采用二阶三点后差方式进行离散，黏性项采用二阶中心差分近似，对流项的空间离散采用迎风通量差分分裂格式，内点使用三阶迎风差分离散，边界点采用二阶迎风差分格式。边界条件给定如下：对于远场边界，将入流边界点的速度项指定为自由流条件(由已知的翅膀运动确定)，而压力项由内点外插；出流边界点压力项等于自由流静压，而速度项由内点外插得到。翅膀表面采用无渗透和无滑移条件，压力由动量方程的法向分量获得。关于计算方法的详细描述参见文献[11]。
本文所用计算程序已多次在以前的研究中使用过，例如文献[3, 12-13]，其正确性已得到充分的验证；通过与拍动模型果蝇翅^[14]、周向转动模型翅^[15]和采用“合拢”运动的模型翅^[16]上的非定常气动力测量结果的比较，研究所使用的计算流体力学(CFD)计算程序获得的非定常气动力与实验测量结果的一致性较好。本文中所用模型翅计算网格为O-H型网格，大小为107×107×126(法向×周向×展向)，其平面形状如图 1(a)所示。壁面网格法向间距为0.001 5c；远场边界约为20c。无量纲时间步长取0.02(以c/U进行无量纲化)。基于文献[15]中对网格密度、时间步长以及算法和程序的验证，其工作表明，本文使用的数值计算方法是可靠的，各计算参数的选取也是合适的。
求解Navier-Stokes方程后，各离散网格点上每一时刻的速度分量和压力都可以得到。翅膀上的气动力(包括举力V、水平力H、升力L和阻力D)可以通过翅面上的压力和黏性力求得。举力系数C_V、水平力系数C_H、升力系数C_L和阻力系数C_D分别定义为C_V=V/(0.5ρU²S)，C_H=H/(0.5ρU²S)，C_L=L/(0.5ρU²S)，C_D=D/(0.5ρU²S)，ρ为流体的密度，S为翅膀的面积。
1.3 蜂蝇形态学及运动学参数 本文所用蜂蝇飞行数据取自文献[9]，相关形态学参数有：总质量m=88.88 mg，翅长R=11.2 mm，平均弦长c=2.98 mm，翅面积二阶矩折合半径r₂=0.55 R，单个翅膀面积S=33.34 mm²。蜂蝇悬停时翅膀运动学参数有：拍动幅角Φ=107.1°，拍动频率n=164 Hz，拍动平面与水平面的夹角β≈0°，翻转时间Δt_r^*为拍动周期的25%。
基于以上飞行参数，可以确定参考速度U=3.78 m/s，雷诺数Re=781.6，拍动周期T=U/(nc)=7.72。由于α_d和α_u在实验测量中误差相对较大，气动力矩对于?的变化也较为敏感，因此，昆虫悬停飞行时的α_d、α_u和?需要通过力和力矩的平衡(翅膀产生的平均举力平衡体重，平均水平力为零)微调确定，具体实现过程参考文献[17]，最终确定出?、α_d和α_u分别为2.8°、31.8°和31.8°^[17]。
2 结果与讨论 文献[13, 18]中为探讨横向气动导数的产生机理，给出了在侧向风速v=0.15U情形下昆虫左右翅上的气动力曲线及翅膀展向截面上的涡量分布，可以看出，侧风使左右翅上的气动特性产生了一定的差异。为进一步探讨侧风对拍动翅气动特性的影响，本文分别计算了模型翅在正常悬停无侧风和有侧风时的绕流情况，并求解得到了翅上的气动力。下面从侧风的方向和强度2个方面分析侧风作用下拍动翅气动特性的变化及其原因。
2.1 不同方向的侧风对拍动翅气动特性的影响 为研究不同方向的侧风对拍动翅气动特性的影响，本文中选定来流速度v=±0.10U(“+”表示侧风由翅尖吹向翅根，“-”表示侧风由翅根吹向翅尖)。图 3给出了存在侧风时拍动翅上升力系数C_L和阻力系数C_D在一个拍动周期内随时间历程的变化曲线。为了便于比较，平衡飞行(蜂蝇正常悬停飞行，即无侧风)时的力曲线也包含在图 3中。

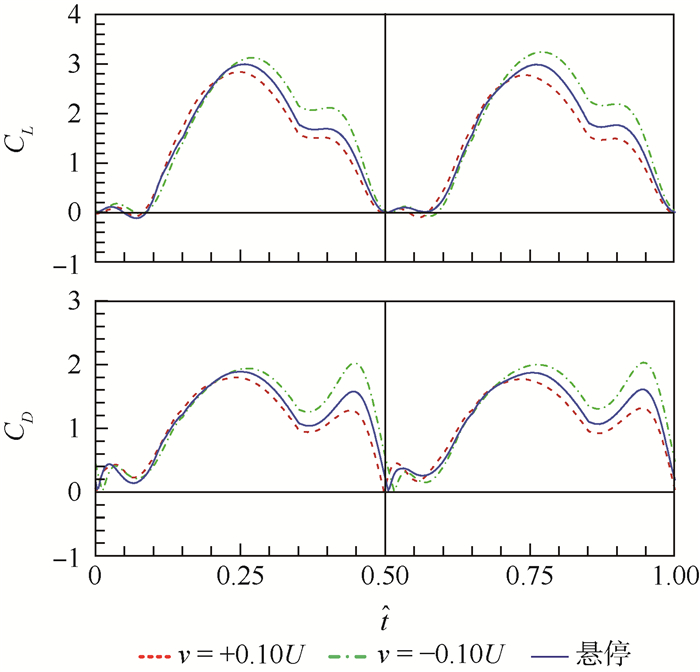图 3 拍动翅上升力系数和阻力系数在一个拍动周期内随时间的变化曲线 Fig. 3 Time courses of lift coefficient and drag coefficient of flapping wing in one flapping cycle

图选项

从图 3中可以看出，不同方向的侧风对拍动翅气动力特性的影响有着明显的不同。在下拍和上拍的后半阶段(和≈0.75~1.00)，当侧风从翅尖吹向翅根时，拍动翅上的升力系数C_L与阻力系数C_D较之正常悬停时有所减小；当侧风从翅根吹向翅尖时，升力系数和阻力系数较之正常悬停时有所增加。在下拍和上拍的前半阶段，即≈0~0.25和≈0.50~0.75，侧风从翅尖吹向翅根与侧风从翅根吹向翅尖2种情况下，拍动翅上升力系数和阻力系数与正常悬停时的差别均相对较小。
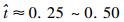
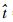
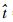
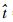
为便于考察侧风对拍动翅上气动力产生影响的原因，此处将不同方向侧风作用时拍动翅上的C_L和C_D与正常悬停(无侧风)情况下相应各量的差值分别用ΔC_L和ΔC_D表示。图 4给出了v=+0.10U和v=-0.10U的侧向风速下拍动翅上ΔC_L和ΔC_D在一个拍动周期内随时间的变化。当侧风从翅尖吹向翅根时，下拍过程的前半阶段(≈0~0.22)，拍动翅上升力和阻力均增大(ΔC_L和ΔC_D为正)，在后半阶段(≈0.23~0.50)，升力和阻力均减小(ΔC_L和ΔC_D为负)，而且后半阶段的ΔC_L和ΔC_D在数值上明显大于下拍前半阶段的ΔC_L和ΔC_D；对于侧风从翅根吹向翅尖的情况而言，结果与侧风从翅尖吹向翅根的情况相反，下拍的前半阶段(≈0~0.22)，ΔC_L和ΔC_D为负，后半阶段(≈0.23~0.50)，ΔC_L和ΔC_D为正。2种侧风情况下，上拍过程中ΔC_L和ΔC_D随时间的变化规律与下拍时类似。

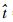
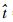
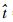
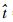
图 4 在侧风时(v=±0.10U)拍动翅上ΔCL和ΔCD随时间的变化 Fig. 4 Time courses of ΔCL and ΔCD of flapping wing with lateral wind (v=±0.10U)

图选项

存在侧风时，上述ΔC_L和ΔC_D的变化可能存在2个方面的原因。根据图 5所示，在模型翅的拍动过程中，侧风速度v可分解为垂直翅展向的分量(记作v_r=vsin?)和平行翅展向的分量(记作v_a=vcos?)。其中，垂直翅展向的速度分量v_r可改变拍动翅的相对速度；通常情况下，昆虫翅膀拍动时翅上会存在前缘涡(LEV)^{[1, 19]}，而平行翅展向的速度分量v_a可改变拍动翅上前缘涡的轴向速度。现针对图 4中所示ΔC_L和ΔC_D的变化做具体分析。

图 5 v=±0.10U时侧风垂直翅展向分量和平行翅展向分量示意图 Fig. 5 Schematic of chordwise component and spanwise component of lateral wind of wing at v=±0.10U

图选项

1) 原因1。由于速度分量v_r的影响，在下拍的前半阶段(≈0~0.25)，侧风从翅尖吹向翅根时，拍动翅上将看到比正常悬停状态下大的相对速度，而侧风从翅根吹向翅尖时，拍动翅上将看到比正常悬停状态下小的相对速度；下拍的后半阶段效果相反。这在一定程度上解释了为什么下拍前半阶段侧风从翅尖吹向翅根时拍动翅C_L和C_D增大，侧风从翅根吹向翅尖时拍动翅C_L和C_D减小，而在下拍后半阶段，侧风从翅尖吹向翅根时C_L和C_D减小，侧风从翅根吹向翅尖时C_L和C_D增大。可将上述效果称为相对速度效应。
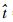
2) 原因2。对于不同方向的侧风情况来说，速度分量v_a会对翅膀上前缘涡产生不同的影响。图 6给出了在下拍某一时刻拍动翅展向截面的涡量图，其中实线和虚线分别代表正涡量和负涡量，最外层无量纲等涡量线大小为2，间隔为3。可以看出，v=-0.10U时拍动翅上的前缘涡(见图 6(a))明显比v=+0.10U时拍动翅上的前缘涡(见图 6(b))要集中。这是因为v=+0.10U时拍动翅看到一近似由翅尖到翅根的展向相对流动，而v=-0.10U时拍动翅则是看到一近似由翅根到翅尖的展向相对流动。从翅尖到翅根的展向流动将减小前缘涡的轴向流速，使得前缘涡比悬停状态下更为松散，从而使气动力减小；而从翅根到翅尖的展向流动将增大前缘涡的轴向流速，使得前缘涡比悬停状态下更为集中，从而产生更大的气动力。将这种效果称为前缘涡轴向速度效应。

图 6 v=±0.10U时下拍阶段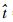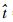=0.25翅膀上距翅根0.6R~0.9R处截面等涡量线 Fig. 6 Vorticity contours at wing sections 0.6R-0.9R from wing root during downstroke at =0.25 and lateral wind velocity v=±0.10U

图选项

以上2种效应的共同作用使得翅膀上的气动力产生如图 4所示的变化。
2.2 不同强度的侧风对拍动翅气动特性的影响 为考察侧向风速的强度对拍动模型翅气动特性的影响，本文中选取了4个同向的侧向风速(v=+0.05U, +0.10U, +0.15U和+0.20U)进行模拟计算。图 7给出了模型翅在这4个同向侧风下升力系数C_L和阻力系数C_D在一个拍动周期内随时间的变化曲线。为便于比较，正常悬停飞行(无侧风)时的力曲线也包含在图 7中。

图 7 不同侧向风速下和正常悬停飞行(无侧风)时拍动翅上升力系数和阻力系数在一个拍动周期内随时间的变化曲线 Fig. 7 Time courses of lift coefficient and drag coefficient of flapping wing in one flapping cycle under different lateral winds and normal hovering flight (with no lateral wind)

图选项

从图 7中可以看出，当来流从翅尖吹向翅根时，在下拍和上拍的后半阶段(≈0.25~0.50和≈0.75~1.00)，拍动翅上升力系数C_L与阻力系数C_D较之正常悬停飞行(无侧风)时有所减小，而且随着侧向风速的增大，这种气动力上的差别愈加明显；在下拍和上拍的前半阶段，即≈0~0.25和≈0.50~0.75，拍动翅上升力系数C_L与阻力系数C_D与悬停无侧风时差别相对较小。不同强度的同向侧风作用下，拍动翅上的气动力相对悬停无侧风时的变化情况类似，仅存在数值上的差别，气动特性产生变化的原因亦相同，是相对速度效应和前缘涡轴向速度效应共同作用的结果。由于存在不同强度的侧向风速时，拍动翅上气动特性仅差异程度不同，此处不再逐一进行分析。
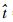
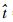
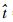
3 结论 1) 不同方向的侧风对拍动翅气动力特性的影响有着显著的不同。在下拍和上拍的前半阶段，侧风从翅尖吹向翅根与侧风从翅根吹向翅尖2种情况下，拍动翅上升力和阻力与无侧风时的差别均相对较小。在下拍和上拍的后半阶段，侧风从翅尖吹向翅根时拍动翅上的升力与阻力较之无侧风时有所减小；侧风从翅根吹向翅尖时，升力和阻力较之无侧风有所增加。
2) 侧风对拍动翅气动特性的改变包含2个流动机制的贡献：①相对速度效应，指侧风的弦向分量会改变拍动翅的相对速度从而改变气动力；②前缘涡轴向速度效应，指侧风的展向分量会改变拍动翅上前缘涡轴向速度，从翅根吹向翅尖的侧风使前缘涡较集中，而从翅尖吹向翅根的侧风使前缘涡较分散，造成拍动翅上气动力改变。
3) 不同强度的同向侧风下，拍动翅上的气动力相对悬停无侧风时的变化情况类似，仅存在数值上的差别。

参考文献

[1]	ELLINGTON C P, VAN DEN BERG C, WILLMOTT A P, et al. Leading-edge vortices in insect flight[J].Nature, 1996, 384: 626–630.DOI:10.1038/384626a0
[2]	BIRCH J M, DICKINSON M H. Spanwise flow and the attachment of the leading-edge vortex on insect wings[J].Nature, 2001, 412(6848): 729–733.DOI:10.1038/35089071
[3]	SUN M, TANG J. Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion[J].Journal of Experimental Biology, 2002, 205(1): 55–70.
[4]	MOU X L, LIU Y P, SUN M. Wing motion measurement and aerodynamics of hovering true hoverflies[J].Journal of Experimental Biology, 2011, 214(17): 2832–2844.DOI:10.1242/jeb.054874
[5]	DUDLEY R, ELLINGTON C. Mechanics of forward flight in bumblebees:Ⅱ.Quasi-steady lift and power requirements[J].Journal of Experimental Biology, 1990, 148(1): 53–88.
[6]	MENG X G, SUN M. Wing kinematics, aerodynamic forces and vortex-wake structures in fruit-flies in forward flight[J].Journal of Bionic Engineering, 2016, 13(3): 478–490.DOI:10.1016/S1672-6529(16)60321-9
[7]	SHEN C, SUN M. Dynamic flight stability of a model dronefly in vertical flight[J].Acta Mechanica Sinica, 2014, 30(6): 828–838.DOI:10.1007/s10409-014-0110-1
[8]	SHEN C, SUN M. Power requirements of vertical flight in the dronefly[J].Journal of Bionic Engineering, 2015, 12(2): 227–237.DOI:10.1016/S1672-6529(14)60115-3
[9]	LIU Y, SUN M. Wing kinematics measurement and aerodynamics of hovering droneflies[J].Journal of Experimental Biology, 2008, 211(13): 2014–2025.DOI:10.1242/jeb.016931
[10]	ELLINGTON C. The aerodynamics of hovering insect flight.Ⅲ.Kinematics[J].Philosophical Transactions of the Royal Society of London.Series B, Biological Sciences, 1984, 305(1122): 41–78.DOI:10.1098/rstb.1984.0051
[11]	ROGERS S E, KWAK D, KIRIS C. Numerical solution of the incompressible Navier-Stokes equations for steady-state and time-dependent problems[J].AIAA Journal, 1991, 29(4): 603–610.DOI:10.2514/3.10627
[12]	SUN M, XIONG Y. Dynamic flight stability of a hovering bumblebee[J].Journal of Experimental Biology, 2005, 208(Pt 3): 447–459.
[13]	ZHANG Y, SUN M. Dynamic flight stability of a hovering model insect:Lateral motion[J].Acta Mechanica Sinica, 2010, 26(2): 175–190.DOI:10.1007/s10409-009-0303-1
[14]	SUN M, WU J H. Aerodynamic force generation and power requirements in forward flight in a fruit fly with modeled wing motion[J].Journal of Experimental Biology, 2003, 206(17): 3065–3083.DOI:10.1242/jeb.00517
[15]	WU J H, SUN M. Unsteady aerodynamic forces of a flapping wing[J].Journal of Experimental Biology, 2004, 207(7): 1137–1150.DOI:10.1242/jeb.00868
[16]	SUN M, YU X. Aerodynamic force generation in hovering flight in a tiny insect[J].AIAA Journal, 2006, 44(7): 1532–1540.DOI:10.2514/1.17356
[17]	WU J, SUN M. Control for going from hovering to small speed flight of a model insect[J].Acta Mechanica Sinica, 2009, 25(3): 295–302.DOI:10.1007/s10409-009-0241-y
[18]	XU N, SUN M. Lateral dynamic flight stability of a model bumblebee in hovering and forward flight[J].Journal of Theoretical Biology, 2013, 319: 102–115.DOI:10.1016/j.jtbi.2012.11.033
[19]	DICKINSON M H, LEHMANN F O, SANE S P. Wing rotation and the aerodynamic basis of insect flight[J].Science, 1999, 284(5422): 1954–1960.DOI:10.1126/science.284.5422.1954