无源定位具有探测距离远、电磁隐蔽性好等优点，已成为各国研究的热点^[1]。以卫星为平台的无源定位系统不受地理位置和气候条件的限制，还可以进行远距离隐蔽侦察，可以及时、准确地发现目标，在民用和军事领域均具有广阔的应用前景^[2-3]。
双星无源定位较多星无源定位而言具有系统简单、易于实现特点。常见的双星无源定位体制有测角交叉定位^[4]、测向和时差^[5-6]、测向和频差^[7]以及时差和频差^[8]等定位体制。在空间电子侦察中应用较为广泛的是双星时差频差定位体制。由于双星定位中的时差、频差和地球球面方程都是关于未知辐射源位置的非线性函数，求解目标辐射源位置时需要对三元高次非线性方程组求解，但是非线性方程组求解还存在许多问题。常见的求解方法有泰勒系数展开法(Taylor-Series, TS)^[9-10]、多维标度定位法(Multidimensional Scaling, MDS)^[11]、半正定松弛(Semidefinite Relaxation, SDR)^[12]以及约束总体最小二乘法(Constrained Total Least Square, CTLS)^[13]等方法。文献[14]给出了在已知辐射源位置高度前提下的双站到达时间差(Time Difference of Arrival, TDDA)和到达频率差(Frequency Difference of Arrival，FDOA)联合定位的解析解，通过求解一元六次方程得到侦察站与辐射源的距离，并且认为当卫星1位置矢量、两卫星位置矢量差以及两卫星速度矢量差三者共面时无解。文献[15]对其进行简化，提出了在两卫星运动速度矢量近似相等时可以将其简化为求解一元四次方程问题，可以简化计算，同时减少虚根数量。
双星TDOA和FDOA无源定位通常是以低轨卫星和地球同步卫星组合，构成双星时频差条件，实现对目标辐射源的定位技术，这样可以增加基线长度，有效提高定位精度^[16]。但是双星无源定位过程中会存在卫星1位置矢量、两卫星位置矢量差以及两卫星速度矢量差三者共面甚至共线情况，文献[14]在对三元高次非线性方程组进行线性转化过程中丢掉了部分信息，造成无法观测定位。本文在文献[14-15]基础上进行了深入的研究，针对卫星1位置矢量、两卫星位置矢量差以及两卫星速度矢量差三者共面情况进行了详细理论分析和推导，给出了一般情况下矩阵非满秩时的目标位置的解析解，并且给出了双星TDOA和FDOA无法观测定位条件，进行了仿真实验并与理论误差对比。
1 双星时频差定位原理 双星时频差无源定位系统原理构成如图 1所示，假定地球为一个正球面，地球半径为R，已知高度为h_T的地面固定目标辐射源位置坐标为X_T=[x_T??y_T??z_T]^T，则

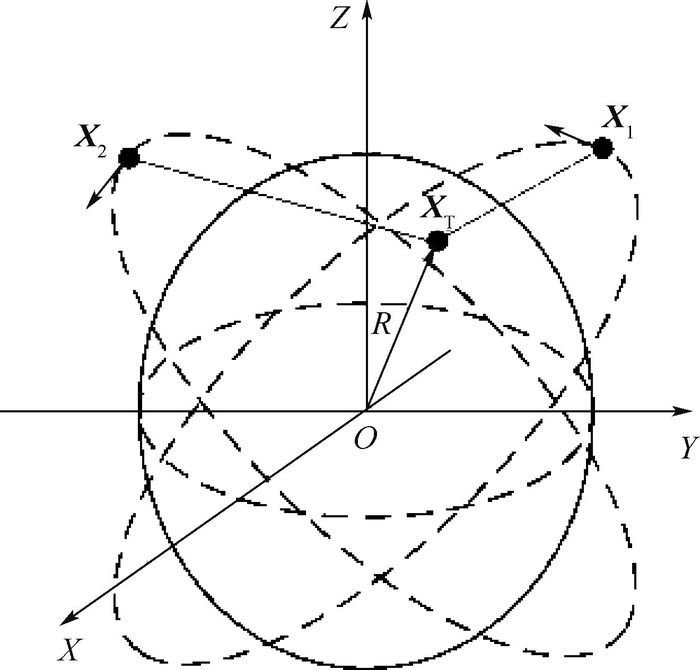图 1 双星时频差无源定位示意图 Fig. 1 Schematic of dual-satellite passive location using TDOA and FDOA

图选项

(1)

某时刻两卫星位置矢量为X_i=[x_i??y_i??z_i]^T，速度矢量为V_i=[v_xi??v_yi??v_zi]^T。两卫星与目标辐射源距离为

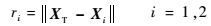(2)

设目标辐射源信号到达两卫星的时间差为τ，则

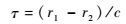(3)

式中：c为电磁波传播速度。
目标辐射源信号到达两卫星的多普勒频率为

(4)

式中：λ为信号波长。
到达两卫星的多普勒频差为Δf_d，则

(5)

2 定位解析解 本节此推导地球为正球面情况下，双星TDOA和FDOA无源定位空间位置解析解。为了表示方便，令：

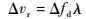(6)

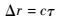(7)

由时差、频差公式，可以得到

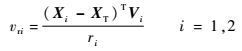(8)

(9)

(10)

联立方程，得到方程组为

(11)

(12)

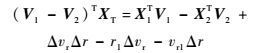(13)

采用矩阵形式表示，令：

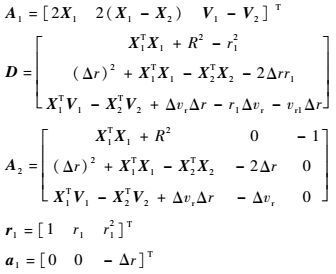则可以得到

(14)

为了描述方便，定义矩阵A₁为伪观测矩阵，描述目标位置状态经过其作用，变成可观测的含有未知数r₁、v_r1的矩阵。从矩阵A₁可以看出，其包含卫星1位置矢量、两卫星位置矢量差以及两卫星速度矢量差。文献[14]给出了伪观测矩阵A₁可逆情况下的双星TDOA和FDOA无源定位解析解，本文重点推导伪观测矩阵A₁不可逆(即卫星1位置矢量、两卫星位置矢量差以及两卫星速度矢量差共面)情况下的双星TDOA和FDOA无源定位解析解。
2.1 共面但不共线 当卫星1位置矢量、两卫星位置矢量差以及两卫星速度矢量差三者共面但不共线时，伪观测矩阵A₁秩为2。当Rank(A₁)=2时，此时det(A₁)=0，即det (A₁^T)=0，则0是A₁和A₁^T的特征值。对矩阵A₁^T进行特征分解，其中向量q=[q₁??q₂??q₃]^T是矩阵A₁^T的0特征值对应的特征向量，则

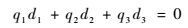(15)

式中：

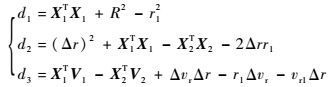对式(15) 进行整理化简得到

(16)

式中：

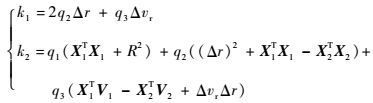1) 若q₃=0，即两卫星的位置矢量X₁, X₂共线，则可以直接利用式(16)，通过求解一元二次方程得到r₁的值。
然后将式(8) 代入式(13)，可以得到

(17)

令：

因为矩阵A₁的秩为2，即矩阵F₁的秩也为2，则

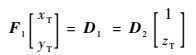(18)

可以得到

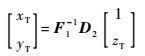(19)

将式(19) 代入式(1)，即可得到关于z_T的一元二次方程，通过求解一元二次方程即可得到z_T值。再将z_T代入式(19)，即可得到目标位置。
2) 若q₃≠0，联立式(8) 和式(16)，可得

(20)

构造新的伪观测矩阵B₁，则


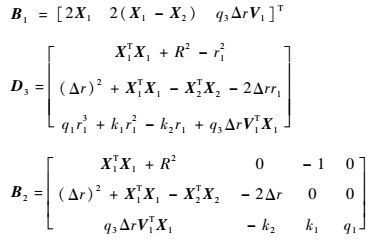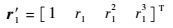若矩阵B₁为满秩可逆，则

(21)

此时，将式(21) 代入式(1)，得到关于r₁的一元六次方程，通过求解方程即可得到r₁的值。
将得到的r₁值代入式(21) 即可得到目标位置X_T值。
需要说明的是，当两卫星速度矢量相同时，此时q₁=q₂=0，式(21) 就可以简化成一个一元四次方程，与文献[15]所述情况相同。因此，可以认为文献[15]是上述情况下的一个特例。
若矩阵B₁为不可逆，对矩阵B₁^T进行特征分解，其中向量p=[p₁??p₂??p₃]^T是矩阵B₁^T的0特征值对应的特征向量，则

(22)

式中:

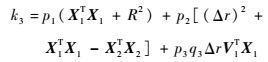通过求解上述一元三次方程，即可得到r₁的值。
令：

则

(23)

此时，可以得到

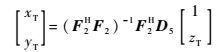(24)

同理，将式(24) 代入式(1)，即可得到z_T的一元二次方程，通过求解一元二次方程即可得到z_T值。再将z_T代入式(24)，即可得到目标位置。
2.2 共线 当卫星1位置矢量、两卫星位置矢量差以及两卫星速度矢量差三者共线时，伪观测矩阵A₁的秩为1。此时有2种情况：
1) 若矢量X₁、X₂、V₁和V₂在同一直线上，此时无法观测。
2) 矢量X₁、X₂和V₁－V₂在同一直线上，而X₁、X₂和V₁、V₂不在同一直线上。
令：

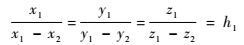(25)

(26)

则

(27)

(28)

利用式(27)、式(28) 即可得到r₁, v_r1值，并将其代入式(8)，可以得到

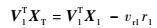(29)

(30)

构造新的伪观测矩阵C₁，则

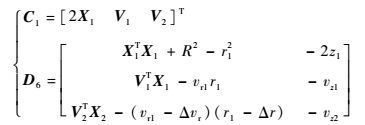由于矩阵C₁的秩为2不可逆，联立方程式(11)、式(29)、式(30) 构成方程组，可以通过求解方程组用z_T表示x_T、y_T：

(31)

将式(31) 代入式(1)，通过求解一元二次方程得到z_T值，再代入式(31) 得到最终X_T值。
3 性能分析 3.1 误差理论分析 文献[15]给出了已知高度双星TDOA和FDOA无源定位的定位误差为

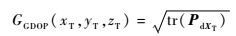(32)

式中：


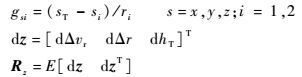3.2 仿真分析 为研究不同情况下两星TDOA和FDOA联合定位算法的定位性能，分别针对几种不同情况下的定位性能进行仿真分析。在仿真过程中，假定两卫星时差测量误差的均方根σ_τ=10 ns，频差测量误差的均方根σ_Δfd=5 Hz，辐射源信号载频f_c=10 GHz。
仿真条件1??考虑两卫星位置矢量共线情况，两卫星经纬度坐标均为[45° 45°]，速度矢量均为[50 000-3 504.5]m/s，高度相距100 km，其中卫星1距地面高度为600 km，卫星2距地面高度为700 km，定位误差分布的仿真结果如图 2所示，图中等值线为定位误差值，单位为km。

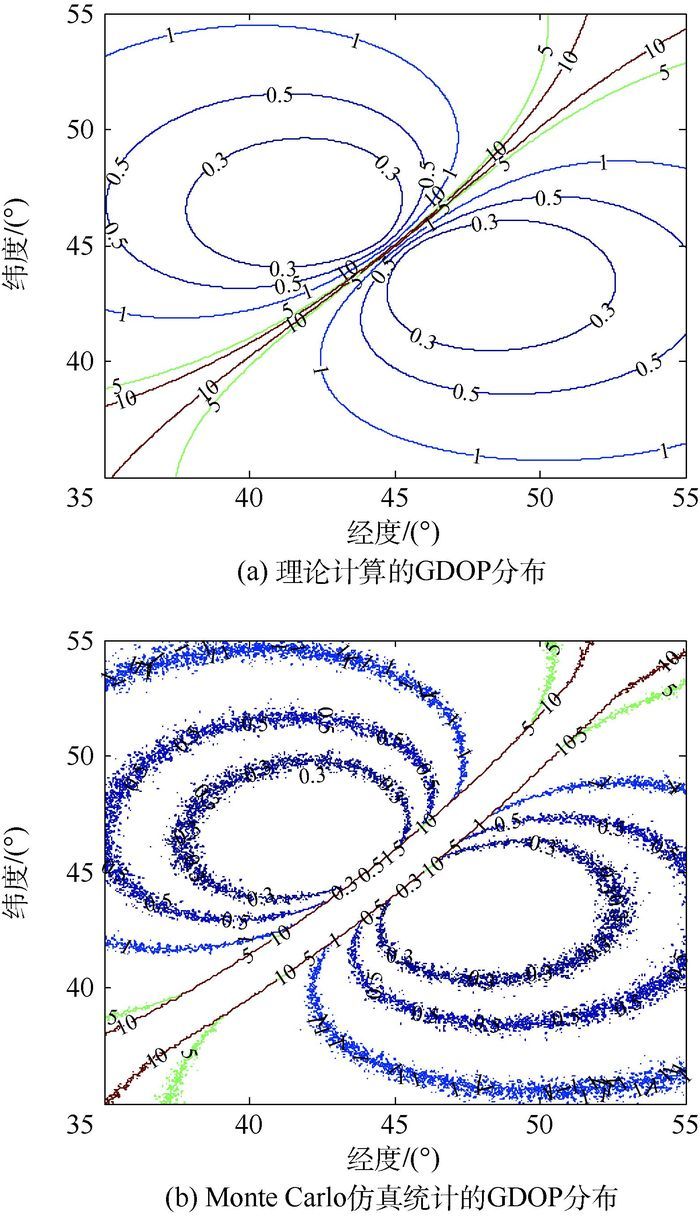图 2 两卫星位置矢量共线时定位误差分布 Fig. 2 Location error distribution when position vectors of dual satellites are collinear

图选项

仿真条件2??考虑两卫星位置矢量不共线，但速度相同时情况。两卫星经度坐标分别为[44.42° 45°]和[45.58° 45°]，速度矢量均为[50 000 －3 504.5]m/s，两卫星距地面高度均为650 km，定位误差分布的仿真结果如图 3所示，图中等值线为定位误差值，单位为km。

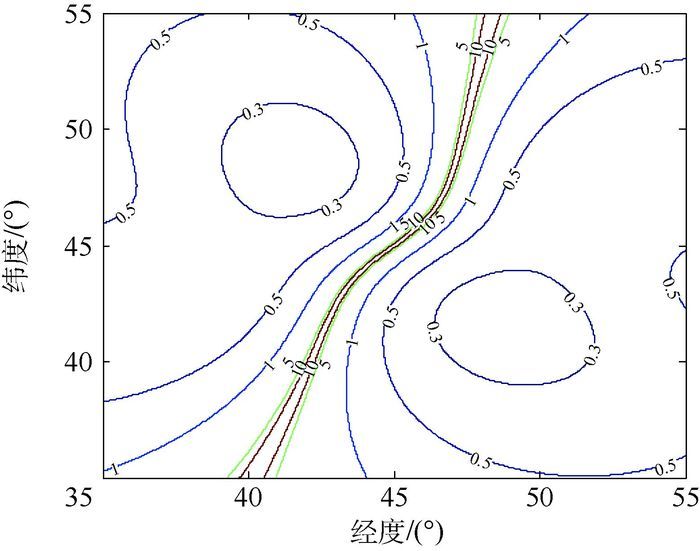图 3 三矢量共面但不共线时定位误差分布 Fig. 3 Location error distribution when three vectors are co-planar but non-collinear

图选项

仿真条件3??考虑两卫星位置矢量不共线，速度也不相同时情况。两卫星经纬度坐标分别为[44.42° 45°]和[45.58° 45°]，速度矢量分别为[50 000 －3 504.5]m/s和[5 000 －97.14－3 503.2]m/s，两卫星距地面高度均为650 km，定位误差分布的仿真结果如图 4所示，图中等值线为定位误差值，单位为km。

图 4 三矢量不共面时定位误差分布 Fig. 4 Location error distribution when three vectors are not co-planar

图选项

从图 2(a)和图 2(b)对比可以发现，在两卫星位置矢量共线情况下，Monte Carlo仿真统计误差与理论计算误差的GDOP(Geometrical Dilution of Precision)分布基本一致，从而验证了本文所提算法的正确性。
从图 2可以看出，当两卫星位置矢量共线时，在卫星所在位置的星下点有一条不可定位的线性区域带，其大致方向为平行于速度矢量，且与两卫星连线方向垂直。其主要原因是等时差线与等多普勒差线几乎相切，导致定位误差急剧增大。图 3、图 4同样存在一不可定位区域带，其原因与图 2相同，但是由于其两卫星连线面或者速度运动方向相对较复杂，所以呈现出一条弯曲的曲线带。
从图 2~图 4对比可以发现，虽然两卫星位置矢量共线时不可定位区域要大于两卫星位置矢量不共线情况，但是在星下点附近两卫星共线时定位误差小于0.3 km的区域要明显大于两卫星位置矢量不共线情况。此外，当三矢量共面但不共线时，其定位误差小于0.3 km和0.5 km的区域要明显大于三矢量不共面情况。因此，卫星1位置矢量、两卫星位置矢量差以及两卫星速度矢量差三者共面时在一定情况下可以改善星下点区域的定位精度。
4 结论 本文针对低秩条件下双星无源定位问题进行研究，主要包括：
1) 给出了卫星1位置矢量、两卫星位置矢量差以及两卫星速度矢量差三者共面情况下的解析解，解决了三元高次非线性方程组在线性转化过程中由于信息丢失造成无法观测的问题。
2) 指出了双星TDOA和FDOA无源定位过程中无法观测情况，即当且仅当两卫星位置矢量和速度矢量四者共线时无法观测。
3) 当两卫星位置矢量共线时，可以将复杂的一元六次方程求解问题简化为一元二次方程求解，减小虚根数量，降低求解复杂度。
4) 双星无源定位时当卫星1位置矢量、两卫星位置矢量差以及两卫星速度矢量差三者共面时可以提高星下点某些特定区域定位精度。
通过仿真实验与理论误差进行对比，验证了本文所提算法的有效性。

参考文献

[1]	常啸鸣, 张晓林, 张强. 基于加权矩阵的TDOA多站无源定位算法[J].北京航空航天大学学报, 2011, 37(11): 1378–1383. CHANG X M, ZHANG X L, ZHANG Q. Method of TDOA multistation passive location based on weighted matrix[J].Journal of Beijing University of Aeronautics, 2011, 37(11): 1378–1383.(in Chinese)
[2]	杨宇翔, 张汇川. 同步三星目标运动状态快速检测方法[J].北京航空航天大学学报, 2014, 40(10): 1392–1398. YANG Y X, ZHANG H C. Fast algorithm of motion state detection based on tri geo-satellites[J].Journal of Beijing University of Aeronautics, 2014, 40(10): 1392–1398.(in Chinese)
[3]	狄慧, 刘渝, 杨健. 基于径向加速度精估计的PSO单星无源定位[J].宇航学报, 2014, 35(9): 1036–1043. DI H, LIU Y, YANG J. PSO single satellite passive localization based on radial acceleration accurate estimation[J].Journal of Astronautics, 2014, 35(9): 1036–1043.(in Chinese)
[4]	白晶, 王国宏, 王娜, 等. 测向交叉定位系统中的最优交会角研究[J].航空学报, 2009, 30(2): 298–304. BAI J, WANG G H, WANG N, et al. Study on optimum cut angles in bearing-only location systems[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(2): 298–304.(in Chinese)
[5]	曲长文, 徐征, 李炳荣, 等. 一种新的基于角度和时差的稳健定位跟踪算法[J].信号处理, 2011, 27(2): 230–235. QU C W, XU Z, LI B R, et al. A novel robust algorithm for passive location and tracking with angles and time difference of arrival measurements[J].Signal Processing, 2011, 27(2): 230–235.(in Chinese)
[6]	YIN J H, WAN Q, YANG S W, et al. A simple and accurate TDOA-AOA localization method using two stations[J].IEEE Signal Processing Letters, 2016, 23(1): 144–148.DOI:10.1109/LSP.2015.2505138
[7]	贾兴江, 周一宇, 郭福成. 双/多机测角频差定位算法研究[J].信号处理, 2011, 27(1): 37–42. JIA X J, ZHOU Y Y, GUO F C. Research on hybrid DOA and FDOA passive localization using dual/multiple aircrafts[J].Signal Processing, 2011, 27(1): 37–42.(in Chinese)
[8]	CAO Y L, PENG L, LI J Z, et al. A new iterative algorithm for geolocating a known altitude target using TDOA and FDOA measurements in the presence of satellite location uncertainty[J].Chinese Journal of Aeronautics, 2015, 28(5): 1510–1518.DOI:10.1016/j.cja.2015.08.015
[9]	FOY W H. Position location solutions by Taylor-series estimation[J].IEEE Transaction on Aerospace and Electronic Systems, 1976, AES-12(2): 187–194.DOI:10.1109/TAES.1976.308294
[10]	TPRRIERI D J. Statistical theory of passive location systems[J].IEEE Transaction on Aerospace and Electronic Systems, 1984, AES-20(2): 183–198.DOI:10.1109/TAES.1984.310439
[11]	WEI H, PENG R, WAN Q, et.al. Multidimensional scaling analysis for passive moving target localization with TDOA and FDOA measurements[J].IEEE Transaction on Signal Processing, 2010, 58(3): 1677–1688.DOI:10.1109/TSP.2009.2037666
[12]	WANG G, LI Y, ANSARI N. A semidefinite relaxation method for source localization using TDOA and FDOA measurements[J].IEEE Transaction on Vehicle Technology, 2013, 62(2): 853–862.DOI:10.1109/TVT.2012.2225074
[13]	YU H, HUANG G, GAO J. Constrained total least-squares localization algorithm using time difference of arrival and frequency difference of arrival measurements with sensor location uncertainties[J].IET Radar Sonar & Navigation, 2012, 6(9): 891–899.
[14]	HO K C, CHAN Y T. Geolocation of a known altitude object from TDOA and FDOA measurements[J].IEEE Transaction on Aerospace and Electronic Systems, 1997, 33(3): 770–783.DOI:10.1109/7.599239
[15]	郭福成, 樊昀. 双星时差频差联合定位方法及其误差分析[J].宇航学报, 2008, 29(4): 1381–1386. GUO F C, FAN Y. A method of dual-satellites geolocation using TDOA and FDOA and its precision analysis[J].Journal of Astronautics, 2008, 29(4): 1381–1386.(in Chinese)
[16]	杨宇翔, 夏畅雄, 同武勤. 高低轨双星定位中的时变时频差参数估计[J].信号处理, 2012, 28(10): 1465–1474. YANG Y X, XIA C X, TONG W Q. Estimation of the time varying TDOA and FDOA in the GEO-LEO dual-satellites location system[J].Signal Processing, 2012, 28(10): 1465–1474.DOI:10.3969/j.issn.1003-0530.2012.10.017(in Chinese)