删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于稀疏核增量超限学习机的机载设备在线状态预测*

本站小编 Free考研考试/2021-12-25
对飞机关键部件工作状态进行准确预测，对提升故障的早期识别能力、提高系统的可靠性、增加飞行的安全性具有重要意义[1-2]。
在机载设备状态监测中，由于采集信号的传感器种类繁多，采集的数据表现出类别多、信息结构各异、强非线性等特点，致使一些传统的预测方法出现单步预测不精确、多步预测无效的问题。在这种情况下，核方法[3-5]体现出了潜在的优势。核方法通过Mercer核的使用，可以将低维空间中的特征向量映射到一个高维甚至是无穷维的再生核Hilbert空间(Reproducing Kernel Hilbert Space, RKHS)中，以至于许多非线性问题在其中可以找到线性解。2011年，Huang等[6-7]提出了核超限学习机(Extreme Learning Machine with Kernel，KELM)，并通过理论分析与实验证明，相比于支持向量积和最小二乘支持向量积，在回归任务中，其具有更好的稳定性，并且可以在一个更快的速度下实现与前者相似的泛化性能。
然而在实际应用中，状态监测数据通常是序贯产生的。为了满足在线应用的需要，文献[8]提出了基于核的增量ELM(Kernel-based Incremental ELM, KB-IELM)，它与其他核在线学习算法[9-13]一样，随着学习过程的进行，模型阶数将随着训练样本的增加而线性增长，致使算法存在过学习的风险，模型每次更新需要花费大量的时间[9]，在非平稳环境中，不利于跟踪系统的时变动态特征[11]。为此，引入稀疏化过程成为了普遍的共识[14]。稀疏化的难点在于如何判断一个新的观测样本属于冗余信息还是可以学习的信息。针对这一问题，科研人员提出了一些有效的稀疏测量方法。例如，一致性准则[10]、积累一致性准则[12]、近似线性独立(Approximate Linear Dependency, ALD)准则[15]和Surprise测量[16]等。
科研人员也设计出了针对KB-IELM的在线稀疏化方法。文献[17]基于传统滑动时间窗，提出了带有遗忘机理的在线KELM (Online KELM with Forgetting mechanism, FOKELM)。文献[18]在文献[17]的基础上，将Cholesky因式分解引入在线学习，有效提升了算法效率。一般来说，样本的重要性通常由隐藏在时间序列中的内在结构决定[19]，因此滑动时间窗方法并不能保证新添加的样本对现阶段模型的贡献最大。文献[20]提出了基于ALD的核在线序贯ELM (ALD based Kernel Online Sequential ELM, ALD-KOS-ELM)，在该算法中，一个新的输入样本仅仅当在一个预设的误差阈值下无法被当前字典元素线性表示时才被插入字典中。文献[21]提出了在线KELM (Online KELM, OKELM)，该算法采用快速留一交叉验证实现对训练样本有区别的取舍。
上面提到的大多数稀疏化方法，稀疏效果的好坏完全依赖于稀疏参数，而稀疏参数的确定通常基于经验选择，缺乏理论性指导。为此，本文针对机载设备在线状态预测，提出了一种稀疏核增量超限学习机(Sparse Kernel Incremental ELM, SKIELM)算法。对于字典选择，在RKHS中基于瞬时信息测量提出了一种构造与修剪策略相结合的稀疏化方法。通过在构造阶段在线最小化字典冗余，在修剪阶段最大化字典元素的瞬时条件自信息量，选择具有预定规模的稀疏字典。本文提出的稀疏化方法不用预先定义稀疏参数，不依赖于训练样本的先验信息，是一种无监督的稀疏化方法。对于KB-IELM的核权重更新问题，提出改进的减样学习算法，其可以实现字典中任一个核函数删除后剩余核函数Gram矩阵的逆矩阵的前向递推更新。通过实例分析表明，本文所提算法适用于机载设备在线状态预测，并且可以实现更高的预测精度。
1 问题描述 假设有一数据流S={(u1, d1), (u2, d2), …}，ui∈Rn，di∈R。一个多输入单输出的ELM模型可以表示为[7]
(1)

式中：wj和bj为隐层神经元的学习参数；β=[β1, β2, …, βL]T为输出权重向量；G(wj·ui+bj)表示第j个隐层神经元对应输入ui的输出；h(ui)为从n维输入空间到L维隐层特征空间的特征映射，即h(ui)=[G(w1·ui+b1), G(w2·ui+b2), …, G(wL·ui+bL)]。
ELM在保证训练错误最小的同时，使输出权重的范数||β||最小。通过解优化方程可以得到输出权重为
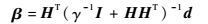(2)

式中：H=[hT(u1), hT(u2), …, hT(ut)]T为所有输入的映射矩阵；d=[d1, d2, …, dt]T为输入对应的目标值；γ为正则化参数。应用Mercer条件定义核矩阵G=HHT。令k(·, ·)为一个核函数，则有G(i, j)=h(ui)·hT(uj)=k(ui, uj)，因此得到ELM的核化形式为

式中：α=(γ－1I+HHT)－1d为核函数的权重向量。
显然当t→∞时，算法的计算负担将无法承受。为此构造字典Dt={k(c1, ·), k(c2, ·), …, k(cmt, ·)}，则在时刻t，有，ci为第i个核函数的中心，{c1, c1, …, cmt}?{u1, u2, …, ut}，αi, t为t时刻第i个核函数的系数，mt为当前模型的阶数，且mt?t。所以对于时刻t+1的输入ut+1，对应的输出可以表示为
(3)

在式(3) 中有2个关键问题要处理：① 稀疏字典的选择；② 核权重向量的更新。下面将对这2个问题进行详细研究。
2 基于瞬时信息测量的字典选择 时刻t的学习系统记作T(ft, Dt, αt)，ft为系统函数，Dt为字典，αt为核函数权重，为了表示方便，将其简记为Tt。在时刻t+1，当一个新的训练样本(ut+1, dt+1)获得时，得到一个新的核函数k(ut+1, ·)。此时，潜在的字典记作Dt={Dt, k(ut+1, ·)}。为判断是否接受k(ut+1, ·)，基于信息理论首先给出下面2个定义。
定义1??假设在Tt下，观测样本ut+1的瞬时后验概率为pt(ut+1|Tt)，则ut+1中包含的可以转移到字典Dt的信息量定义为ut+1在时刻t的瞬时条件自信息量，即I(ut+1|Tt)=－ln pt(ut+1|Tt)，其中，对数的底为e，在下文中如无特殊说明对数均以e为底。
定义2??假设在Tt下，字典Dt的元素个数为mt，核中心ci(1≤i≤mt)的瞬时后验概率为pt(ci|Tt)，则字典Dt在时刻t所具有的平均自信息量定义为Dt的瞬时条件熵，即

在实际问题中，没有先验知识或假设，数据的概率分布函数(Probability Distribution Function, PDF)是很难得到的。一种合理的方法就是通过给定的样本去估计PDF。给定一个数据序列U={u1, u2, …, uN}∈Rn，通过核密度估计(Kernel Density Estimator, KDE)得到的PDF可以表示为，θ为核宽度，wi为权重系数，并且有。当采用最大近邻估计准则计算核系数时，可得到?ui∈U, wi=1/N。所以对于字典Dt，在KDE下核中心的瞬时条件PDF表示为
(4)

因此，观测样本ut+1的瞬时条件自信息量和字典Dt的瞬时条件熵分别表示为

在线字典选择策略包括2个阶段：构造阶段和修剪阶段。整个字典选择过程如图 1所示。在下文中规定采用的核函数均为单位范数核，即?u∈U，k(u, u)=1。
图 1 核矩阵Gt的变化过程 Fig. 1 Growing size of kernel matrices Gt
图选项




2.1 构造策略 记et=[1, 1, …, 1]T∈Rmt×1，字典Dt的Gram矩阵为Gt，计算矩阵St=Gt×et，即
(5)

根据KDE，字典Dt中第i个核中心在学习系统Tt下的瞬时条件概率为pt(ci|θ, Tt)=St(i)/mt。所以，字典Dt的瞬时条件熵为
(6)

在t+1时刻，由所有核函数构成的潜在字典Dt={Dt, k(ut+1, ·)}的Gram矩阵记为Gt，且有
(7)

记et=[1, 1, …, 1]T∈R(mt+1)×1，令St=Gt×et，有
(8)

式中：kt=[kθ(c1, ut+1), kθ(c2, ut+1), …, kθ(cmt, ut+1)]T∈Rmt×1；∑kt为kt中所有元素之和。将St和kt代入式(8)，可得到St。
在潜在字典Dt中，第i个核中心的瞬时条件概率为pt(ci|θ, Tt)=St(i)/(mt+1)。所以，潜在字典Dt的瞬时条件熵为
(9)

按照相关定义，字典Dt和Dt的冗余分别为
(10)

(11)

如果Rt＜Rt，说明新的核函数的加入降低了字典的冗余，也就是说提高了字典的平均自信息量，所以新的训练样本被纳入学习模型，并且有，；否则，新的训练样本被视作冗余直接删除，且各参数保持不变。
2.2 修剪策略 当字典的大小满足mt=m时，则在下一时刻将执行修剪策略。目的是要从m+1个潜在元素中选择m个元素。
定义矩阵，, It为m+1阶单位阵。矩阵Gt乘以Et，得到

当潜在字典Dt中第i(1≤i≤m+1) 个元素被删除后，第l(l≠i)个元素的瞬时条件概率为
(12)

根据矩阵Ft可以得到
(13)

由此，删除第i个元素之后剩余元素构成的新字典Dt－i中，元素的瞬时条件自信息量矩阵为

找出Dt－i的元素中具有的最小瞬时条件自信息量，记为
(14)

本文目的是为了最大化字典中每个元素的瞬时条件自信息量，因为每个元素具有的瞬时条件自信息量越大，说明彼此之间越不相似，字典所包含的信息量也越大[16]。因此，要删除的元素的下标可以通过式(15) 确定：
(15)

如果i=m+1，则字典与各参数保持不变，因为新的核函数k(ut+1, ·)被从潜在字典中移除；否则，用k(ut+1, ·)取代第i个核函数k(ci, ·)，并且有由式(16) 计算得到。Gt+1由后续算法得到。
(16)

2.3 字典特性分析 假设在每次修剪过程后得到的μt－i=δ，0＜δ≤ln m。下面对字典的约束等距特性和线性独立作简要分析。
定理1??假设基于瞬时信息测量得到的稀疏字典为Dt={k(ci, ·)}i=1m，则其Gram矩阵的特征值是有界的。如果用λ1≥λ2≥…≥λm表示Gram矩阵的m个特征值，并按降序排列，则有2－me－δ≤λm≤…≤λ1≤me－δ。
证明??在Dt={k(ci, ·)}i=1m中，对于任一个核中心ci(i=1, 2, …, m)，其瞬时条件自信息量必满足：

因为对数运算以e为底，则有

由Gersgorin圆盘定理，对于一个m×m的Gram矩阵G，其每个特征值都位于由m个圆盘所构成的联通区域内。圆盘的中心对应于矩阵G的对角线元素，圆盘的半径为其中心所在行的其余元素绝对值之和。换句话说，对于每一个特征值λk，至少存在一个i∈{1, 2, …, m}使得

所以有

进一步有

由于δ＞0，有0＜e－δ＜1，即e－δ是有界的。因此，特征值λk也是有界的，并且对于单位范数核有2－me－δ≤λm≤…≤λ1≤me－δ。
证毕
定理2??假设基于瞬时信息测量得到的稀疏字典为Dt={k(ci, ·)}i=1m，当满足δ＞ln(m/2) 时，字典满足约束等距特性(Restricted Isometry Property, RIP)，并且存在一个约束等距常数τ，使得τ=me－δ－1。
证明??对于ft(·)=[kθ(c1, ·), kθ(c2, ·), …, kθ(cm, ·)]α，有

应用Courant-Fischer极大极小定理[12, 14]，可以得到和λ1分别为Gram矩阵G的最小和最大特征值。根据定理1，有2－me－δ≤λm，λ1≤me－δ，所以有

式中：τ=me－δ－1。当满足δ＞ln(m/2) 时，有0＜me－δ－1＜1。所以字典满足RIP，并且约束等距常数为τ=me－δ－1。
证毕
定理3??假设基于瞬时信息测量得到的稀疏字典为Dt={k(ci, ·)}i=1m，当满足δ＞ln(m/2) 时，字典元素是线性独立的。
证明??对于字典元素之间的任意线性组合，因为有

根据定理1有，2－me－δ≤λm，所以

由于δ＞ln(m/2)，即2－me－δ＞0，因此当成立时，必有||α||2=0。
证毕
定理3表明，当字典中元素的最小瞬时条件自信息量大于ln(m/2) 时，元素之间是线性独立的。从另一个角度看，当上述条件满足时，字典的Gram矩阵是对角占优的。
3 KB-IELM的核权重更新 3.1 增样学习算法 当字典规模小于m时，如果新的训练样本满足2.1节中的条件，则被用来扩展字典。在KB-IELM中，核权重向量α=(γ－1I+G)－1d。在时刻t，不妨记At=γ－1I+Gt。
在时刻t+1，对于训练样本(ut+1, dt+1)：
(17)

式中：vt=γ－1+1；kt=[kθ(c1, ut+1), kθ(c2, ut+1), …, kθ(cmt, ut+1)]T。
利用块矩阵逆公式，可以得到At+1的逆矩阵，即
(18)

式中：ρt=vt－ktTAt－1kt。
此时，核权重向量更新为αt+1=At+1－1dt+1，为核中心ci对应的目标值。
3.2 改进的减样学习算法 在2.2节情况下，为实现模型递推更新，先将At中的第i行移到第1行，第i列移到第1列。其中，i是通过式(15) 搜索得到的元素下标。这个过程可以表示成和Q为2个m阶的初等矩阵，并且有
(19)

(20)

显然，PPT=E，QQT=E，E为m阶单位矩阵，所以P和Q均为正交矩阵。根据正交矩阵的性质，有P－1=PT, Q－1=QT。进一步，考虑到P=QT，可以得到结论：Q－1=P，P－1=Q。对求逆，得到
(21)

使，将进一步写成如下形式：
(22)

再将写成块矩阵的形式，即
(23)

式中：为At中删除第i行和第i列后的矩阵。
使用块矩阵逆公式有
(24)

式中：。
进一步有
(25)

因此，(At－i)－1可以通过Wt直接求得。在时刻t+1，对于训练样本(ut+1, dt+1)：
(26)

通过块矩阵逆公式可得到At+1－1，即
(27)

式中：。
此时，核权重向量更新为。
一般采用固定记忆规模策略的方法，在加入新样本前删除最旧的样本[17, 21]。本文提出的方法在加入新样本前删除重要性最小的样本，它可能是最旧的，也可能是其他任意一个。所以，改进的算法在保证计算复杂度有限的情况下，可以实现字典中任意一个样本删除后剩余样本的前向递推更新，相比于文献[17, 21]中提出的方法更加灵活。
4 算法流程与复杂性分析 4.1 算法流程 本文提出的SKIELM算法计算流程如下。
步骤1??初始化。设置γ, m和θ，令mt=1，Dt={k(u1, ·)}。计算Gt、At－1、St、H(Dt|θ, Tt)和Rt。
步骤2??当新的训练样本(ut+1, dt+1)到达时，如果mt＜m，计算kt，由式(7)、式(8) 分别计算Gt、St，由式(9) 计算H(Dt|θ, Tt)，由式(11) 计算Rt；否则，进入步骤4。
步骤3??如果Rt＜Rt，由式(18) 计算At+1－1，更新αt+1、Rt+1、St+1和H(Dt+1|θ, Tt)，令mt+1=mt+1, Dt+1={Dt, k(ut+1, ·)}；否则，返回步骤2。
步骤4 ??计算kt，由式(7)、式(8) 分别计算Gt、St；计算Dt－i元素中最小的瞬时条件自信息量μt－i；根据式(15) 寻找可以删除的元素下标i。
步骤5??如果i=m+1，则Dt+1=Dt, 参数αt+1、St+1和Gt+1保持不变，返回步骤2；否则，由式(21)、式(25) 计算，计算kt，由式(27) 计算，更新αt+1、St+1和Gt+1。
步骤6??输出Dt+1和αt+1；返回步骤2。
4.2 复杂性分析 在字典构造阶段，每一次训练过程中，St的时间复杂度为O(mt)，H(Dt|θ, Tt)的时间复杂度为O(mt+1)。在字典修剪阶段，计算Gt和St的时间复杂度均为O(m)；计算Dt－i对应的μt－i的时间复杂度为O(m)；确定可以删除的元素下标的时间复杂度为O(m)。所以，字典选择过程的时间复杂度为O(m)。
在核权重更新过程中，对于增样学习，计算kt的时间复杂度为O(mt)，而计算At+1－1的时间复杂度为O(mt2)。对于减样学习，计算和(At－i)－1的时间复杂度分别为O(m2)和O((m-1)2)，计算kt的时间复杂度为O(m-1)，而计算At+1－1的时间复杂度为O((m-1)2)。所以，总的时间复杂度为O(m2)。
通常m的选择不会太大，因此所提方法满足在线应用的需求。
5 实验分析 仿真实验从训练时间和预测精度2个方面进行设计。预测精度通过均方根误差(Root Mean Square Error, RMSE)、最大预测误差(Maximal Prediction Error, MPE)和平均误差率(Average Error Rate, AER)3个指标来衡量，并且有

在实验中，所有方法均采用高斯核作为核函数，即k(ui, uj)=exp(－||ui－uj||2/2θ2)；核参数θ与正则化参数γ通过网格搜索法获得。实验运行环境为：MATLAB2010a，Windows XP操作系统，Intel Core i3处理器，3.30 GHz主频和2 GB RAM。
5.1 非平稳Mackey-Glass混沌时间序列预测 采用Mackey-Glass混沌时间序列验证本文所提算法的有效性。通过如下时延差分方程得到：

初始条件设为：a=0.2，b=0.1，τ=17，x(0)=1.2，当t＜0时，x(t)=0，时间步长Δ=0.1，利用四阶Runge-Kutta方法求解上述差分方程。此外，一个正弦曲线0.3sin(2πt/3 000) 被添加到原始的时间序列上创建一个非平稳混沌时间序列。采样间隔设为Ts=10Δ，共得到1 201个样本点。实验中令嵌入维数为10，则共有1 191组样本，前991组作为训练样本，后200组作为测试样本。分别用SKIELM、KB-IELM和ReOS-ELM[22]估计非线性模型。其中，ReOS-ELM采用Sigmoid函数作为激活函数，即G(w, b, u)=1/[1+exp(－(w·u+b))]。
实验中3种算法的参数设置如表 1所示，预测结果如表 2所示。
表 1 验1选择的参数设置 Table 1 Selected parameter setting in Experiment 1
算法正则化参数γ核参数θ其他参数
ReOS-ELM2×103L=80
KB-IELM2×1032×102
SKIELM2×1032×102m=80
??注：L为ReOS-ELM中隐层神经元个数。


表选项






表 2 Mackey-Glass时间序列预测结果 Table 2 Prediction results for Mackey-Glass time series
算法训练测试
训练时间/sRMSERMSEMPEAER/%
ReOS-ELM1.062 50.039 30.036 80.089 71.38
KB-IELM38.935 00.012 60.011 70.027 60.98
SKIELM0.502 00.015 30.014 50.031 21.14


表选项






由表 2可以看到，基于核的方法在预测精度上明显优于ReOS-ELM。本文算法在与KB-IELM具有相当的RMSE的同时，大大缩短了算法的训练时间。由图 2可以看到，在整个学习过程中，991组训练样本只有近1/3参与了SKIELM模型的更新，这也是训练时间大大缩减的原因所在。
图 2 Mackey-Glass时间序列学习的样本数量 Fig. 2 Number of learned samples for Mackey-Glass time series
图选项




图 3表示对Mackey-Glass混沌时间序列的预测曲线。由图 3(a)可以看到，3种算法在整体上均可以匹配目标序列，但由图 3(b)的局部图可以看到，本文算法与KB-IELM匹配效果更好，并且可以将预测误差限定在一个很小的范围之内，如图 3(c)所示。因此，本文算法用于时间序列预测是有效的。
图 3 Mackey-Glass时间序列预测曲线 Fig. 3 Prediction curves for Mackey-Glass time series
图选项




5.2 基于飞参数据的飞机发动机状态预测 本节以某型直升机的发动机为例进行状态预测，主要监测数据有发动机扭矩、发动机转速、排气温度、滑油压力、滑油温度和燃油瞬时流量等。所有数据来源于该型机的飞参数据系统。
实验中通过飞参系统共得到100组样本，采样间隔为1 s。规定时间嵌入维数为3，即每个参数的输入样本定义为u(t+1)={u(t), u(t－1), u(t－2)}。这样每个参数就得到97组新样本，其中前67组作为训练样本，后30组作为测试样本。为证明本文算法的优势，将其分别与ALD-KOS-ELM、FOKELM以及OKELM 3种算法进行比较。实验中各算法的正则化参数均设置为γ=2×104，针对不同测试项目其余参数设置如表 3所示。
表 3 实验2选择的参数设置 Table 3 Selected parameter settings in Experiment 2
项目FOKELMALD-KOS-ELMOKELMSKIELM
θmθσθmθm
发动机扭矩5×104305×1042×10-55×104305×10430
发动机转速1×109301×1092×10-81×109301×10930
排气温度1×107301×1072×10-91×107301×10730
滑油温度2×105302×1052×10-92×105302×10530
滑油压力2×104302×1042×10-92×104302×10430
燃油瞬时流量2×105302×1052×10-62×105302×10530
??注：σ为ALD-KOS-ELM的阈值参数；m为其他3种算法的时间窗宽度。


表选项






表 4~表 9为4种算法分别对6个参数在预测数据长度等于20条件下的预测结果。可以看到，相比于其他3种算法，本文算法对于不同的参数均取得了更高的预测精度，并且具有相近或者更短的训练时间。
表 4 飞机发动机扭矩状态预测结果 Table 4 Condition prediction results for torque of aeroengine
算法训练测试
训练时间/
s		RMSE/
(N·m)		RMSE/
(N·m)		MPE/
(N·m)		AER/
%
FOKELM0.034 01.016 70.949 62.044 410.87
ALD-KOS-ELM0.034 50.839 20.955 42.581 49.84
OKELM0.034 40.782 20.962 92.655 610.09
SKIELM0.038 00.752 80.929 22.578 59.76>


表选项






表 5 飞机发动机转速状态预测结果 Table 5 Condition prediction results for rotational speed of aeroengine
算法训练测试
训练
时间/s		RMSE
(r·
min-1)		RMSE/
(r·
min-1)		MPE/
(r·
min-1)		AER/
%
FOKELM0.036 698.919 668.621 0157.500.22
ALD-KOS-ELM0.030 792.516 077.050 0173.710.22
OKELM0.032 994.846 166.927 4149.730.27
SKIELM0.035 988.533 864.282 1149.020.19


表选项






表 6 飞机发动机排气温度状态预测结果 Table 6 Condition prediction results for exhaust gas temperature of aeroengine
算法训练测试
训练时间/sRMSE/KRMSE/KMPE/KAER/%
FOKELM0.034 95.273 62.632 14.860 80.49
ALD-KOS-ELM0.065 23.626 42.840 65.664 60.49
OKELM0.038 83.929 03.131 57.274 90.55
SKIELM0.027 63.481 72.495 35.286 90.47


表选项






表 7 飞机发动机滑油温度状态预测结果 Table 7 Condition prediction results for oil temperature of aeroengine
算法训练测试
训练时间/sRMSE/℃RMSE/℃MPE/℃AER/%
FOKELM0.023 60.167 60.203 80.310 60.52
ALD-KOS-ELM0.072 10.031 90.086 30.138 20.21
OKELM0.031 50.025 30.059 30.100 30.14
SKIELM0.031 30.026 00.059 20.100 00.14


表选项






表 8 飞机发动机滑油压力状态预测结果 Table 8 Condition prediction results for oil pressure of aeroengine
算法训练测试
训练时间/sRMSE/NRMSE/NMPE/NAER/%
FOKELM0.027 50.097 00.108 80.127 13.51
ALD-KOS-ELM0.063 70.039 60.033 70.043 61.05
OKELM0.033 00.036 10.029 70.038 60.92
SKIELM0.026 30.034 30.024 80.033 20.75


表选项






表 9 飞机发动机燃油瞬时流量状态预测结果 Table 9 Condition prediction results for fuel instantaneous flux of aeroengine
算法训练测试
训练
时间/s		RMSE/(L·
min-1)		RMSE/(L·
min-1)		MPE/(L·
min-1)		AER/
%
FOKELM0.028 52.635 86.523 222.729 71.89
ALD-KOS-ELM0.019 63.118 36.564 218.451 22.13
OKELM0.031 42.707 26.547 822.688 61.94
SKIELM0.027 62.567 26.100 522.327 91.82


表选项






以发动机排气温度为例，在预测数据长度等于30的条件下，4种算法的预测曲线如图 4所示。由图 4可以看到，本文算法可以更好地匹配目标序列。同时，不同算法对排气温度的预测误差曲线如图 5所示，显然本文算法在整个预测数据长度内具有更小的预测误差。
图 4 排气温度预测曲线 Fig. 4 Prediction curves of exhaust gas temperature
图选项




图 5 排气温度预测误差曲线 Fig. 5 Prediction error curves of exhaust gas temperature
图选项




对于排气温度，在整个训练过程中，本文算法总共学习的样本数量如图 6所示。对于67个训练样本，最终只有25个样本被用于模型的更新，这样有效删除了冗余样本，提升了计算效率。
图 6 排气温度学习的样本数量 Fig. 6 Number of learned samples for exhaust gas temperature
图选项




6 结论 本文在KB-IELM的基础上，针对其模型膨胀和模型更新问题，提出了一种新的在线学习算法，并用于机载设备状态预测，经实验验证表明：
1) 相比于KB-IELM，通过稀疏化策略的应用，本文算法在保证预测精度损失很小的情况下，大幅缩短了训练时间。
2) 相比于3种采用不同稀疏化策略的KELM在线学习算法，本文算法在具有相似训练时间的情况下，有效提升了预测精度。在预测数据长度等于20的条件下，对发动机6个性能参数预测的整体平均误差率为2.18%，相对FOKELM、ADL-KOS-ELM和OKELM预测精度分别提升了0.72%、0.14%和0.13%。
3) 提出的稀疏化方法从信息理论的角度出发，在实现有价值的样本学习的同时，可以删除冗余信息，保证了模型的简洁。在2个实验中，对训练样本的约减都超过了50%。

参考文献
[1] TIAN Z, QIAN C, GU B, et al. Electric vehicle air conditioning system performance prediction based on artificial neural network[J].Applied Thermal Engineering, 2015, 89: 101–104.DOI:10.1016/j.applthermaleng.2015.06.002
[2] 孙伟超, 李文海, 李文峰. 融合粗糙集与D-S证据理论的航空装备故障诊断[J].北京航空航天大学学报, 2015, 41(10): 1902–1909.
SUN W C, LI W H, LI W F. Avionic devices fault diagnosis based on fusion method of rough set and D-S theory[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(10): 1902–1909.(in Chinese)
[3] YE F M, ZHANG Z B, CHAKRABARTY K, et al. Board-level functional fault diagnosis using multikernel support vector machines and incremental learning[J].IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 2014, 33(2): 279–290.DOI:10.1109/TCAD.2013.2287184
[4] JIE Y. A nonlinear kernel Gaussian mixture model based inferential monitoring approach for fault detection and diagnosis of chemical processes[J].Chemical Engineering Science, 2012, 68(1): 506–519.DOI:10.1016/j.ces.2011.10.011
[5] ZHAO X Q, XUE Y F, WANG T. Fault detection of batch process based on multi-way kernel T-PLS[J].Journal of Chemical and Pharmaceutical Research, 2014, 6(7): 338–346.
[6] HUANG G B, ZHOU H, DING X, et al. Extreme learning machine for regression and multiclass classification[J].IEEE Transactions on Systems, Man and Cybernetics-Part B:Cybernetics, 2011, 42(2): 513–529.
[7] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine:Theory and application[J].Neurocomputing, 2006, 70(1-3): 489–501.DOI:10.1016/j.neucom.2005.12.126
[8] GUO L, HAO J H, LIU M. An incremental extreme learning machine for online sequential learning problems[J].Neurocomputing, 2014, 128: 50–58.DOI:10.1016/j.neucom.2013.03.055
[9] ZHAO S L, CHEN B D, ZHU P P, et al. Fixed budget quantized kernel least-mean-square algorithm[J].Signal Processing, 2013, 93(9): 2759–2770.DOI:10.1016/j.sigpro.2013.02.012
[10] RICHARD C, BERMUDEZ M, HONEINE P. Online prediction of time series data with kernels[J].IEEE Transactions on Signal Processing, 2009, 57(3): 1058–1067.DOI:10.1109/TSP.2008.2009895
[11] GAO W, CHEN J, RICHARD C, et al. Online dictionary learning for kernel LMS[J].IEEE Transactions on Signal Processing, 2014, 62(11): 2765–2777.DOI:10.1109/TSP.2014.2318132
[12] FAN H J, SONG Q, XU Z. Online learning with kernel regularized least mean square algorithms[J].Knowledge-Based Systems, 2014, 59: 21–32.DOI:10.1016/j.knosys.2014.02.005
[13] DIETHE T, GIROLAMI M. Online learning with (multiple) kernels:A review[J].Neural Computation, 2013, 25(3): 567–625.DOI:10.1162/NECO_a_00406
[14] HONEINE P. Analyzing sparse dictionaries for online learning with kernels[J].IEEE Transactions on Signal Processing, 2015, 63(23): 6343–6353.DOI:10.1109/TSP.2015.2457396
[15] ENGEL Y, MANNOR S, MEIR R. The kernel recursive least-squares algorithm[J].IEEE Transactions on Signal Processing, 2004, 52(8): 2275–2285.DOI:10.1109/TSP.2004.830985
[16] LIU W F, PARK I, PRINCIPE J C. An information theoretic approach of designing sparse kernel adaptive filters[J].IEEE Transactions on Neural Networks, 2009, 20(12): 1950–1961.DOI:10.1109/TNN.2009.2033676
[17] ZHOU X R, LIU Z J, ZHU C X. Online regularized and kernelized extreme learning machines with forgetting mechanism[J].Mathematical problems in engineering, 2014, 2014: 1–11.
[18] ZHOU X R, WANG C H. Cholesky factorization based online regularized and kernelized extreme learning machines with forgetting mechanism[J].Neurocomputing, 2016, 174: 1147–1155.DOI:10.1016/j.neucom.2015.10.033
[19] GU Y, LIU J F, CHEN Y Q, et al. TOSELM:Timeliness online sequential extreme learning machin[J].Neurocomputing, 2014, 128: 119–127.DOI:10.1016/j.neucom.2013.02.047
[20] SIMONE S, DANILO C, MICHELE S, et al. Online sequential extreme learning machine with kernel[J].IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(9): 2214–2220.DOI:10.1109/TNNLS.2014.2382094
[21] 张英堂, 马超, 李志宁, 等. 基于快速留一交叉验证的核极限学习机在线建模[J].上海交通大学学报, 2014, 48(5): 641–646.
ZHANG Y T, MA C, LI Z N, et al. Online modeling of kernel extreme learning machine based on fast leave-one-out cross-validation[J].Journal of Shanghai Jiaotong University, 2014, 48(5): 641–646.(in Chinese)
[22] HUYNH H T, WON Y. Regularized online sequential learning algorithm for single-hidden layer feedforward neural networks[J].Pattern Recognition Letters, 2011, 32(14): 1930–1935.DOI:10.1016/j.patrec.2011.07.016


相关话题/计算 序列 信息 实验 测试
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于多模型的不等长序列数据关联算法*
    作为一种时间序列，不等长序列数据的关联是异类传感器融合必须解决的问题，其根本方法是对不等长度序列数据相似度的挖掘和度量，特别是干扰条件下量测序列出现突变点的情况。文献[1-15]相继研究了时间序列相似度的查询，形成了一系列序列度量的方法，离散傅里叶变换[1-3]、奇异值分解[4]、离散小波变换[5- ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 冲压空气涡轮泵的温控节流孔计算方法*
    冲压空气涡轮(RAT)应急系统是飞机安全的最后保障，在飞机发动机和电源功能全部丧失的情况下，RAT应急能源系统将空气的动能转换为电能/液压能，提供飞机基本操纵所需能源。RAT系统一般由冲压涡轮、液压泵/发电机和收放装置组成，共有2个工作状态：①收回状态，液压泵静止，不输出功率；②伸出状态，RAT弹出 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 电路测试响应信号的GP-KSVD稀疏重构算法*
    傅里叶变换、小波变换、奇异值分解等方法在信号处理领域中得到了广泛的应用与发展[1]，与此同时，信号的稀疏表示理论也逐渐成为研究热点，在信号去噪[2]、数据压缩[3]、盲源分离以及特征提取等领域都有应用。傅里叶变换以及小波变换中的信号表示是基于正交基的，因此需要保证基函数系的完备性和正交性，保证固有最 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 一种航天器太阳电池阵供电能力计算方法*
    航天器依靠太阳电池阵为设备供电，电池阵供电能力是影响航天器方案设计以及飞行任务规划的重要因素[1-3]。在航天器设计阶段，太阳电池阵供电能力分析可以优化帆板构型和布局，运营阶段，结合航天器轨道和姿态进行供电能力分析，可优化飞行任务规划，确保航天器能量平衡[4-5]。航天器电池阵供电能力受太阳光入射角 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • AVB网络流量整形帧模型端到端延迟计算*
    音视频桥接技术(AVB)是由IEEE802.1AVB工作组(AVBTG)[1]定义的音视频流服务技术，已被车载电子系统等关键嵌入式领域考虑采用[2-4]，是很具潜力的下一代实时网络标准[5-8]。AVB采用基于信用量的整形(CBS)算法对音视频流量进行整形，通过对不同类型流量设定统一的逻辑带宽进行限 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 面向地震应急响应的互联网信息处理*
    根据中国地震局官网统计得出，从2007年1月1日至2016年5月31日近10年间灾害性的中国及周边地区5级以上地震352起，世界7级以上地震197起[1]，其中多数地震都给人类的生命财产造成巨大损失。特别是2008年5.12汶川8.0级地震，受灾面积十万多平方公里，造成遇难和失踪人口87703人，直 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 基于计算力矩法的眼内手术机器人的重力补偿*
    眼科手术对医生的操作精度及稳定性有着非常高的要求，借助先进的机器人技术进行精密的眼科手术已成为国内外眼科研究的热点。视网膜静脉阻塞等眼内手术[1-3]的典型过程是将末端器插入眼内，并绕插入点进行转动或移动，应用于该类手术的机器人均具有远程运动中心(RemoteCenterofMotion,RCM)机 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 基于FMECA信息的测试性验证试验样本分配方法*
    基于故障注入的测试性验证试验是国内外普遍采用的考核产品测试性水平的方式[1-3]。在确定试验样本量后，从故障模式集中将一定数量的样本选取并分配到产品的各个组成单元是试验的一项关键技术[4-6]。目前国内外普遍采用基于产品的结构层次和故障率的分层抽样方法实施的样本分配，该方法能够有效反映受试对象的故障 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 烟气覆盖表面红外温度测量的实验分析*
    在很多领域中，物体表面的温度都是非常重要的监测参数，对其进行在线连续稳定测量具有重要的实用价值[1-2]。目前，实际应用中一般都采用接触式的测量方法，如热电偶、热电阻等[3-4]。接触式测温的测量精度高，但会对被测物体原本温度场产生影响，且氧化、还原和腐蚀等恶劣测温条件会造成热电偶等测温元件的损坏。 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • VHF/UHF波段发射机互调抑制比测试方法研究*
    为了有效利用和科学管理无线频谱资源，必须对无线电设备间的电磁兼容性(EMC)进行分析和预测。在无线电设备发射机发射的电磁信号中，不仅存在有用信号，还存在谐波发射、杂散发射、带外发射和互调发射等无用信号。准确地掌握这些无用信号的发射特性是进行频谱分析和预测的基础。发射机互调(IM)是由于发射机末级功率 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.