磁偶极子跟踪问题主要有解析反演^[1-4]、离线寻优^[5]以及滤波估值^[6-7]3类求解方法。滤波算法由于能够从带噪观测数据中实时估计目标状态, 因此得到了较为广泛的研究。采用滤波算法进行磁偶极子跟踪的主要困难在于高维、强非线性条件下的滤波初始条件不易确定, 而初始条件恰是决定磁偶极子跟踪性能的关键因素^[8]。
对于磁偶极子跟踪这样的高维、强非线性和大初始误差的滤波估计问题, 粒子滤波^[9]虽然能够克服非线性问题, 但其所需的粒子数量仍然随着问题维数规模的扩大呈几何级增长^[10], 故基本的粒子滤波算法无法用于磁性目标实时定位问题。目前已有研究采用了卡尔曼滤波算法来建议分布抽样, 再进行重采样的解决方案, 但在实时应用时计算量仍过大, 且在权值计算中需要很高的数位精度, 这对于实际实现也是不利的^[11]。
相比粒子滤波, 在相同的初始条件下, 卡尔曼类滤波器, 如基于直接线性化的扩展卡尔曼滤波器(Extended Kalman Filter, EKF)^[12]、基于Sigma点近似方法的无迹卡尔曼滤波器(Unscented Kalman Filter, UKF)^[13]和求容积卡尔曼滤波器(Cubature Kalman Filter，CKF)^[14], 对于维数并不敏感, 且远远高于粒子滤波的计算效率。然而对于本文研究的磁性目标跟踪, 由于目标模型自身的高阶非线性, 使得现有卡尔曼类滤波算法中的高斯矩近似方法在大初始误差条件下精度严重下降^[15], 仅在给定精确初始条件下才能正常运行, 否则将出现滤波发散。而实际应用的初始值通常难以先验得知。
本文以磁偶极子等效场源模型为基础, 建立磁性目标跟踪的离散状态空间模型, 将磁偶极子目标实时跟踪问题转化为状态空间模型的滤波估值问题; 针对现有卡尔曼类滤波算法在大初始误差条件下容易出现发散的问题, 提出一种递推观测更新卡尔曼滤波算法, 将现有的一步观测更新变换为递推更新过程, 等效降低模型非线性程度; 分别通过仿真实验与实测的运动车辆磁场数据验证了本文提出算法的有效性与优越性。
1 磁性目标跟踪的状态空间描述 利用目标磁场信息进行无源被动跟踪, 实质上是根据事先建立的磁性目标信号数学模型, 通过对某一观测时刻磁场信号的反演计算, 实时估计出下一观测时刻到来之前目标位置、速度和磁矩等参数的连续过程。因此, 本节首先建立磁性目标的等效数学模型。
磁性目标跟踪是通过磁传感器捕获的测量值来估计目标位置、速度和磁矩等信息的连续过程。由于静磁信号的快衰减特性, 其作用范围比较受限, 因此应用场合一般为低动态目标跟踪(如普通车辆、舰船等), 其运动状态可近似为线性运动, 而系统的观测方程则是非线性的。系统的离散状态空间模型(Discrete-time State-Space Model, DSSM)描述如下:

(1)

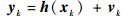(2)

式中：x_k为系统在时刻k时的状态向量；y_k为k时刻的系统观测值；A为状态转移矩阵；h(·)为观测方程；L为过程噪声权重系数矩阵；w_k和v_k－1分别为均值为零的状态噪声和观测噪声, 且假设在估值过程中噪声的统计特性不发生显著变化, 即E[w_k－1w_k－1^T]=D, E[v_k－1v_k－1^T]=R, 观测噪声与状态无关, 即协方差矩阵分别为给定的矩阵Q和R, 且Q=LDL^T。
式(1) 称为离散时间状态转移方程, 式(2) 称为离散时间观测方程。
运动模型用来描述式(1) 中的过程方程。由于磁性目标一般为低动态载体, 因此可将其运动状态建模为线性高斯-马尔可夫模型, 状态转移过程则可以用一个线性变换矩阵来表示, 即在式(1) 中令状态转移矩阵为

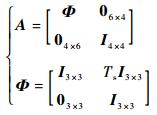(3)

系统状态向量表示为

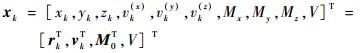(4)

式中：r_k=[x_k, y_k, z_k]^T, x_k、y_k和z_k为目标在坐标系中的位置；v_k=[v_k^(x), v_k^(y), v_k^(z)]^T, v_k^(x)、v_k^(y)和v_k^(z)为目标的运动速度；M₀=[M_x, M_y, M_z]^T, M_x、M_y和M_z为目标在传感器坐标系下的磁矩分量；V为目标体积系数；T_s为采样时间间隔。
过程噪声权重系数矩阵L为

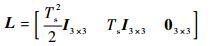对于观测模型, 在目标尺寸相对于目标距离较小的条件下, 由于磁偶极子模型能够很好地描述小尺度静磁源产生的磁场分布, 磁性目标在测量点感应出的磁场B(r)可建模为单磁偶极子模型:

(5)

式中：B(r)=[B_x(r), B_y(r), B_z(r)]^T；为合成磁偶极矩, B₀为环境磁场矢量强度; r为磁偶极子相对于传感器测量点的位置坐标；〈·〉表示向量的内积运算; μ₀=4π×10^-7为真空磁导率。
考虑到背景磁场的影响, 可进一步得到观测方程表达式为

(6)

式中：m_k为k时刻条件下的合成磁偶极矩；B₀主要由地磁场和温漂引起的传感器偏置磁场等组成。
在地磁场环境下, 目标磁矩m与目标的运动方向密切相关, 当且仅当目标做匀速直线运动时, 目标的磁矩可以认为是定值。为保证对状态向量的可观测性, 使用2个三轴磁场传感器输出的6维数据组成观测向量, 即y_k=(B_{x1, k}, B_{y1, k}, B_{z1, k}, B_{x2, k}, B_{y2, k}, B_{z2, k})^T。
观测向量会受到传感器自噪声以及环境噪声影响, 可通过对模型式(2) 中的v_k项建模得到。根据中心极限定理和实际测量的噪声分布拟合规律, 可近似认为其满足高斯分布, 即v_k~N(0, R), R为传感器自噪声及环境噪声总和的协方差矩阵。
联合式(1)~式(4) 和式(6)，即可构成磁性目标跟踪的离散状态空间模型描述, 从而可利用非线性滤波估计算法进行求解。
2 递推更新卡尔曼滤波 本节从降低增益、逐步递推更新的思路提出一种新的扩展卡尔曼滤波算法, 使非线性影响在迭代更新过程中每一步均有所减弱, 从而整体上降低大初始误差导致的大线性化误差对于滤波器的影响。
对于当前观测时刻k, 将一次观测更新考虑为由N次递推完成, 当前次递推的估计结果由上一次递推结果获得。在当前次递推开始时利用上一次递推估计值对非线性观测方程利用一阶Taylor展开进行线性化。

(7)

式中：为上一次递推的状态估计值；为h(x)在点上的雅可比矩阵。
由于、均为已知, 故利用式(7) 构造新的观测值y_k^*为

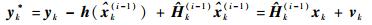(8)

则此时非线性观测方程等效转化为线性观测方程。在此条件下, 考虑式(9) 所示线性观测更新等式：

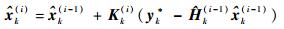(9)

式中：为观测更新后状态估计值；K_k⁽ⁱ⁾为滤波增益。
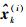
根据式(9), 可得估计误差为

(10)

式中：e_k⁽ⁱ⁾=x_k－x_k⁽ⁱ⁾。
故对于第1次递推更新有e_k⁽⁰⁾=x－x_k^－, 因此

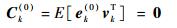(11)

式中：C_k⁽ⁱ⁾为k时刻第i次递推条件下状态误差与观测噪声之间的相关矩阵。
进一步地, 注意到, 则

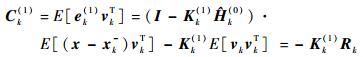(12)

此时计算得到的误差与滤波增益表达式均与标准卡尔曼滤波是一致的, 值得注意的是, 从第2次递推更新开始, 由于当前次估计误差与噪声是相关的, 故式(11) 不再成立。综上, 可得相关矩阵的递推等式为

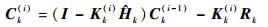(13)

另一方面, 根据式(10) 可得k时刻第i次递推条件下估计误差的均方误差(Mean Square Error, MSE)矩阵, 即误差协方差矩阵为

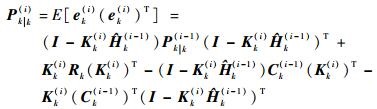(14)

根据式(14) 求tr(P_k|k⁽ⁱ⁾)关于K_k⁽ⁱ⁾的导数, 利用以下矩阵迹求导法则：

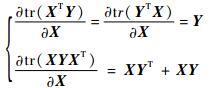(15)

在求导结果中令导数为零, 可得k时刻第i次递推的滤波增益为

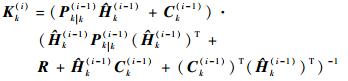(16)

若直接采用式(16) 进行递推更新, 在非线性观测模型条件下, P_k|k⁽ⁱ⁾将进一步收缩, 由于需要进行N次递推, 故根据式(16) 将第i次递推的滤波增益降低为

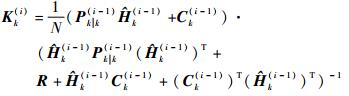(17)

由于磁性目标定位问题仅在观测模型存在非线性时, 因此上述递推开始时的先验估值及先验误差矩阵和可直接通过线性卡尔曼滤波时间更新过程得到, 根据状态模型表达式(1), 可得

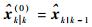
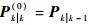
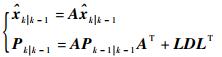(18)

综上所述, 完成时间更新后, 在每个观测时刻, 设置初始条件为, , C_k⁽⁰⁾=0_d×m, 在每个观测到来时刻将式(13)、式(14) 以及式(17) 执行N次, 即可得到迭代更新后的状态及均方误差矩阵估值。
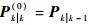
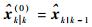
值得注意的是, 将上述算法应用于磁性目标定位, 需在每步部分增益更新计算磁偶极子模型观测函数的雅可比矩阵。数值雅可比矩阵虽然求解简单, 但由于状态维数较高且耗时较长, 解析雅可比矩阵相对数值雅可比矩阵具有更高的运算效率, 因此, 此处求解的是解析雅可比矩阵。
注意到，观测函数对于完整状态量的雅可比矩阵可分解为对子状态量, 即目标位置、磁矩以及体积系数的雅可比矩阵, 即

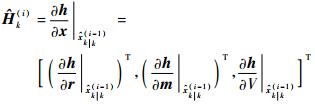(19)

对式(19) 求观测函数相对子状态分量的导数, 即可得到磁性目标观测函数的雅可比矩阵, 根据式(6) 给出的观测方程, 易得各子状态分量的求导结果为

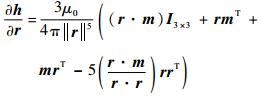(20)

(21)

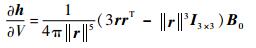(22)

3 结果与分析 为验证本文提出的递推更新卡尔曼滤波器(Recursive Update Kalman Filter, RUKF)的性能, 本节通过设计仿真实验与采用车辆运动通过的实测磁场数据, 分别对本文算法在大初始误差条件下的收敛性能以及实际条件下的有效性进行验证。用于参考对比的经典卡尔曼滤波类算法包括经典的EKF、UKF、CKF以及文献[16]中提出的同样用于处理大初始误差的渐进UKF(PUKF)与渐进CKF(PCKF)算法。
3.1 仿真实验分析 考虑2个三轴磁传感器分别位于空间直角坐标系内点O_{1, 2}=[－50, ±6, 0]^T m处，磁偶极子目标初始位置为r₀=[－150, －150, 40]^T m，初始速度为v₀=[9, 9, 0.6]^T m/s，目标固有磁矩为M₀=10⁶[3, －9, 9]^T A·m²，体积系数为V=10³ m³，过程噪声强度为E[w_k－1w_k－1^T]=0.5I_3×3，观测噪声协方差矩阵为R=σ²I_6×6，σ为传感器的均方根噪声幅度。仿真采样间隔为0.4 s，仿真步数为T_n=75。
初始位置估计值为, R(ψ_n)为在传感器坐标系内绕z轴的旋转矩阵, 用于考察算法在不同初始位置误差程度条件下的性能, ψ_n~U(－Ψ, Ψ)为服从均匀分布的随机旋转角, n=1, 2, …, N_mc, N_mc为Monte Carlo仿真次数; , M₀=[0, 0, 0]^T A·m², ，初始均方误差矩阵为P₀=diag[P₀^r, P₀^v, P₀^M, p₀^V], P₀^r=diag[80², 80², 10²]，P₀^v=diag[2², 2², 2²], P₀^M=diag[10¹², 10¹², 10¹²], p₀^V=1 000。
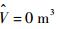
采用EKF、UKF、CKF、PUKF、PCKF和RUKF算法进行100次Monte Carlo仿真对比。其中，RUKF算法的迭代更新次数为N=10, 利用第n次仿真中k时刻状态分量估计结果计算该分量随k变换的均方根误差(Root MSE, RMSE)：

(23)

式中：z_kⁿ为分量在第n次仿真的真实值。
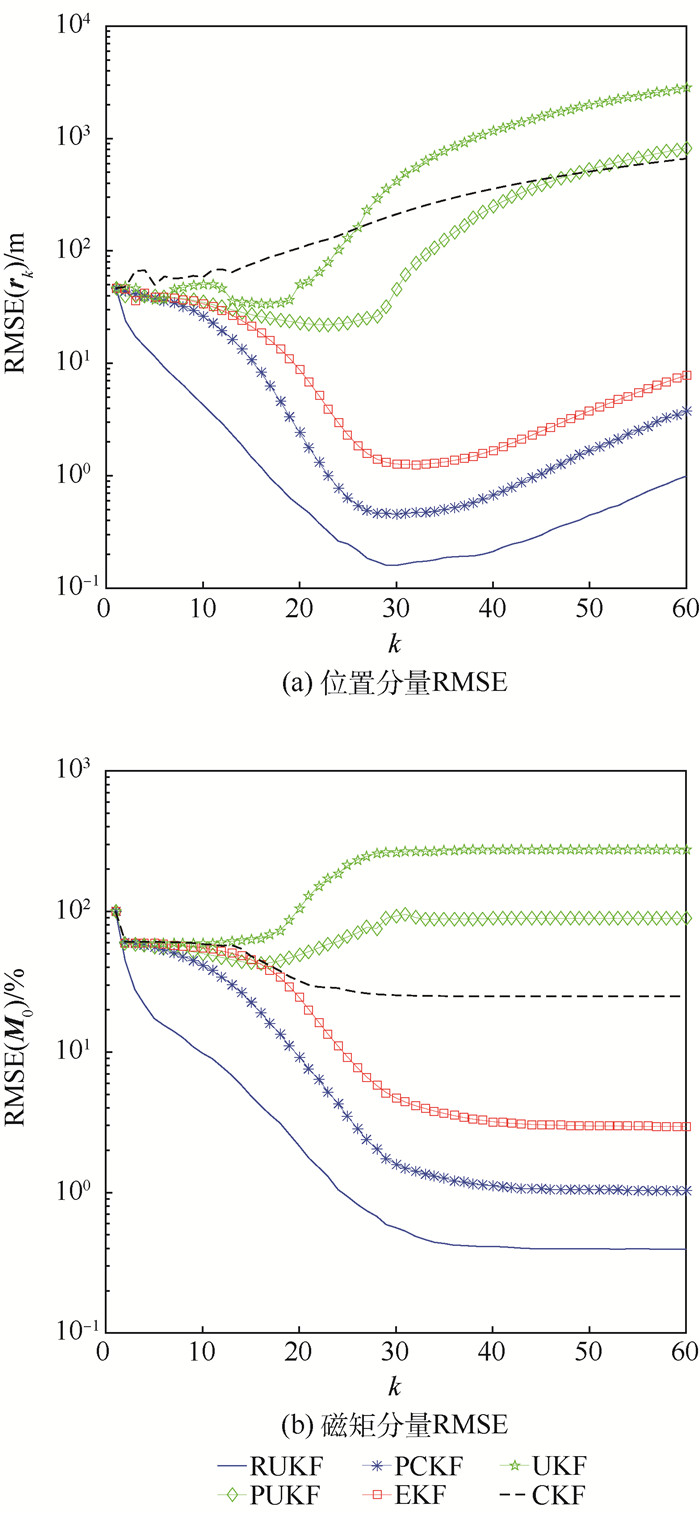
磁性目标跟踪应用最为关心的是目标位置以及磁矩特征。图 1~图 3分别给出了在不同初值位置误差条件下, 位置分量误差RMSE(r_k)与磁矩分量误差RMSE(M₀)的计算结果。其中，对于磁矩常量的估计误差为相对误差，即RMSE(M₀)/||M₀||。

图 1 Ψ=π/3时位置和磁矩分量RMSE Fig. 1 RMSE of position and magnetic moment component at Ψ=π/3

图选项

图 2 Ψ=π/8时位置和磁矩分量RMSE Fig. 2 RMSE of position and magnetic moment component at Ψ=π/8

图选项

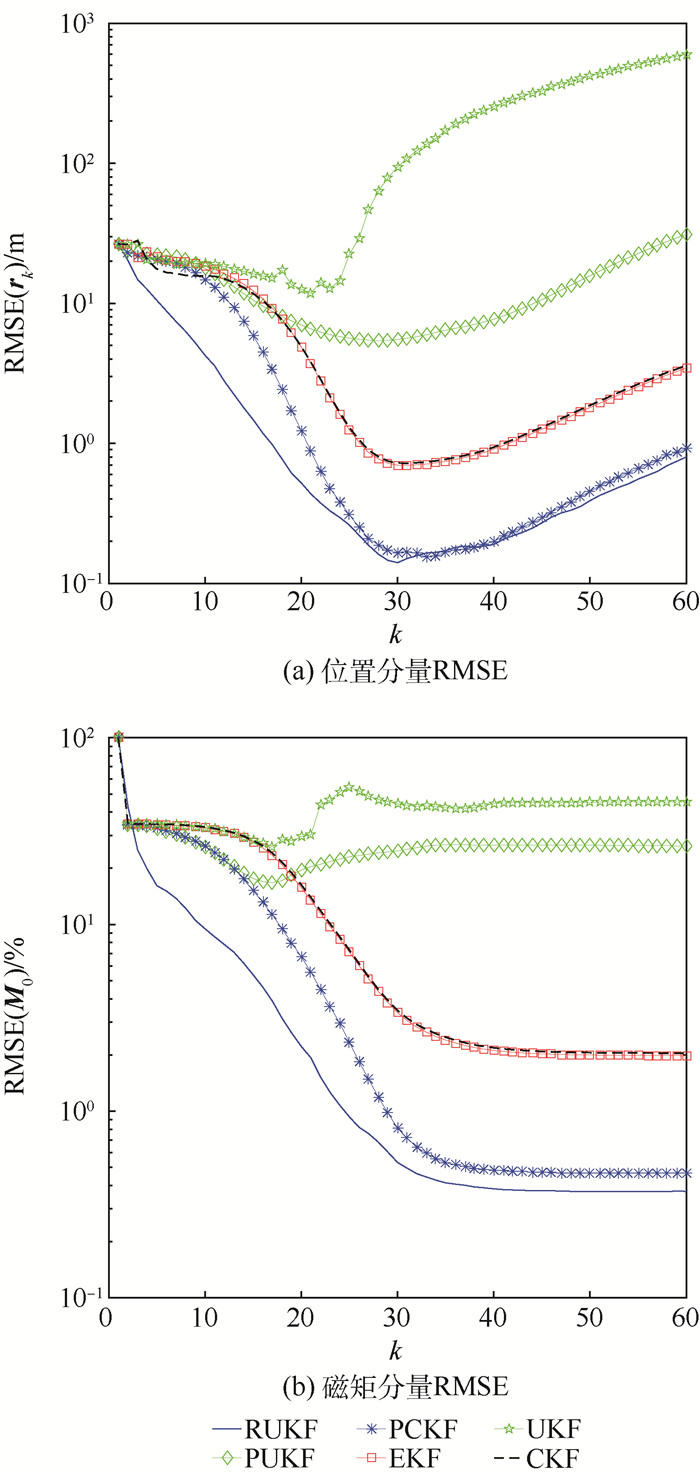图 3 Ψ=π/16时位置和磁矩分量RMSE Fig. 3 RMSE of position and magnetic moment component at Ψ=π/16

图选项

从图 1~图 3中可见, RUKF算法在不同初始误差条件下都给出了一致良好的结果, 受初始误差影响较小, 其他渐进算法的估计性能则随着初值误差减小而提高。特别当Ψ=π/3时, 仅有RUKF算法得到合理的估计误差, 其他算法均不同程度出现较大误差。
同时可以看出, 当目标逐渐远离测量点时, 空间位置(变量)估计误差随信噪比下降而增大, 这是由于动态估计依赖于当前观测信息导致的; 而对于磁矩(常量)估计，则在信噪比达到最高后结果逐渐稳定。
3.2 实测数据测试 为进一步验证本文算法在实测数据条件下的一致有效性, 采用文献[7]中实验采集到的运动车辆磁场实测数据对本文算法及3.1节中的其他对比算法进行测试, 关于实验场景构建的详细说明可见文献[7], 此处仅给出本文算法验证相关的实验条件。实测数据包含了2个三轴磁传感器对一辆从南向直行来转弯至东向的车辆(见图 4)产生磁场的测量结果, 以及2个传感器各自记录的无目标通过时噪声统计量和背景磁场矢量, 这些数据可直接用来对车辆运动轨迹进行跟踪。

图 4 车辆转弯通过测量点 Fig. 4 Vehicle making turn at measuring position

图选项

由于实测条件下难以确定目标状态分量的真实值, 利用估计值和实际观测值计算得到的归一化后验残差来定量评价各个算法性能, 即

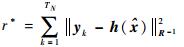(24)

测量数据采样率为100 Hz, 2个三轴磁传感器分别位于宽度为9 m的道路两边, 跟踪坐标系原点位于2个传感器连线的中点, 测量点在跟踪坐标系的坐标分别为[0, ±4.5, 0]^T m, 实验开始时车辆处于南向约20 m处, 速度约为5~7 m/s。
在利用滤波算法进行处理之前, 首先将原始测量数据降采样至12.5 Hz, 以便降低噪声强度和运算时间, 以及去除测量中的野值, 降采样后的测量数据如图 5所示。

图 5 降采样后的运动车辆磁场测量数据 Fig. 5 Motion vehicle magnetic data after downsampling process

图选项

图 6分别给出了在不同初始位置设置条件下, 采用EKF、UKF、CKF、RUKF、PUKF和PCKF算法利用测量数据对图 4中目标车辆进行跟踪的结果。图中：Start即为初始估计位置。显然可见, EKF、UKF和CKF算法对于初始误差是十分敏感的, 仅在初始误差较小, 即初值位置接近实际情况时才能够较为准确地跟踪目标轨迹。而RUKF算法则对初始误差具有较好的鲁棒性, 在不同初始位置条件下都能够给出合理的目标轨迹, 反映了车辆从南向运动转弯至东向的实际运动趋势。

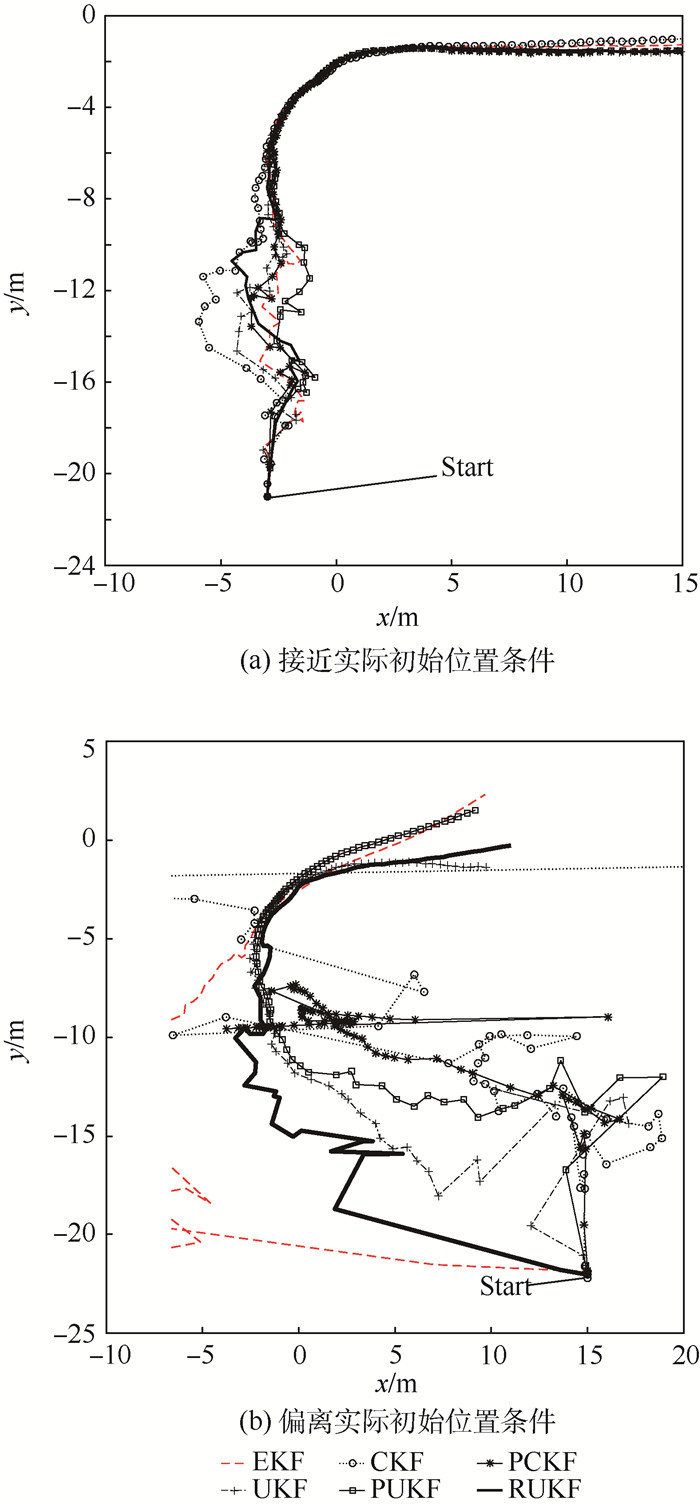图 6 不同初值条件下各算法对实测数据的跟踪处理结果 Fig. 6 Real-world data tracking and processing results by each algorithm under different initializing conditions

图选项

表 1给出了各算法归一化后验残差平方和计算结果。可见，RUKF算法在2次实测实验中均给出了最小的归一化后验残差平方和, 表明RUKF算法的估计结果优于现有算法。
表 1 各算法在不同初值条件下的归一化后验残差平方和 Table 1 Normalized posterior residual square sum for each algorithm under different initializing conditions

算法	r*
	偏离实际初始位置	接近实际初始位置
EKF	9.363×104	9.285×104
UKF	1.179×105	9.635×104
CKF	9.453×105	1.623×107
PUKF	4.722×105	3.725×103
PCKF	1.504×105	2.341×106
RUKF	8.356×104	1.538×103

表选项






4 结论 本文针对磁性目标跟踪问题，建立了以磁偶极子等效场源模型为基础的离散状态空间模型, 提出了一种适于大初始误差情形的RUKF算法。仿真与实测数据测试结果表明：
1) RUKF算法具有良好的准确性和强收敛性, 有效抑制了大初始误差导致的滤波发散, 适于处理实际应用中初始条件未知条件下的磁性目标跟踪问题。
2) 若进一步将RUKF算法与多初值假设方法结合, 可大幅减少并行滤波器数量, 相比现有算法更适合工程实现。
3) 对于一般非线性滤波应用, RUKF算法作为通用算法的性能需针对具体问题, 尤其是包含非线性过程模型的情况进行分析和验证。
致谢    
感谢瑞典Linkoping大学自动控制系Niklas Walhstrom博士提供实测实验数据。
参考文献

[1]	MCAULAY A. Computerized model demonstrating magnetic submarine localization[J].IEEE Transaction on Aerospace and Electronic System, 1977, 13(3): 246–254.
[2]	MCFEE E, DAS Y, ELLINGSON O. Locating and identifying compact ferrous objects[J].IEEE Transactions on Geosciences and Remote Sensing, 1990, 28(2): 182–193.DOI:10.1109/36.46697
[3]	PHAM D, AZIZ S. A real-time localization system for an endoscopic capsule using magnetic sensors[J].Sensors, 2014, 14(1): 20910–20929.
[4]	NARA T, SUZUKI S, ANDO S, et al. A closed-form formula for magnetic dipole localization by measurement of its magnetic field and spatial gradients[J].IEEE Transaction on Magnetic, 2006, 42(10): 3291–3293.DOI:10.1109/TMAG.2006.879151
[5]	王金根, 龚沈光. 基于运动标量磁强计的磁性目标定位问题研究[J].电子学报, 2002, 30(7): 1057–1060. WANG J G, GONG S G. Research on the problem of localizing magnetic target based on motion scalar magnetometer[J].Acta Electronica Sinica, 2002, 30(7): 1057–1060.(in Chinese)
[6]	BIRSAN M. Recursive Bayesian method for magnetic dipole tracking with a tensor gradiometer[J].IEEE Transactions on Magnetics, 2011, 47(2): 409–415.DOI:10.1109/TMAG.2010.2091964
[7]	WAHLSTROM N.Target tracking using Maxwell's equations[D].Linkoping:Linkoping University, 2010.
[8]	BIRSAN M. Recursive Bayesian method for magnetic dipole tracking with a tensor gradiometer[J].IEEE Transactions on Magnetic, 2011, 47(2): 409–415.DOI:10.1109/TMAG.2010.2091964
[9]	DOUCET A, GODSILL S, ANDRIEU S, et al. On sequential Monte Carlo sampling methods for Bayesian filtering[J].Statistics and Computing, 2000, 10(3): 197–208.DOI:10.1023/A:1008935410038
[10]	KOTECHA J H, DJURIC P M. Gaussian particle filtering[J].IEEE Transactions on Signal Processing, 2003, 51(10): 259–260.
[11]	RUDOLPH M, DOUCET A, NANDO F.The unscented particle filter[R].Cambridge:Cambridge University Engineering Department, 2000.
[12]	JAZWINSKI A. Stochastic process and filtering theory[M].New York: Academic Press, 1970.
[13]	SIMON J, JEFFERY U, HUGH D. A new method for the nonlinear transformation of means and covariances in filters and estimators[J].IEEE Transactions on Automatic Control, 2000, 45(3): 477–481.DOI:10.1109/9.847726
[14]	ARASARATNAM I, HAYKIN S. Cubature Kalman filter[J].IEEE Transactions on Automatic Control, 2009, 56(6): 1254–1269.
[15]	MORELANDE M R, GARCIA-FERNANDEZ A F. Analysis of Kalman filter approximations for nonlinear measurements[J].IEEE Transacions on Signal Process, 2013, 61(12): 5477–5484.
[16]	HUANG Y L, ZHANG Y G, LI N, et al.Gaussian approximate filter with progressive measurement update[C]//Proceedings of 54th IEEE Conference on Decision and Control.Piscataway, NJ:IEEE Press, 2015:4344-4349.