在降雨量较大等恶劣天气情况下,机载端和地面站气象条件有较大差异,对应的对流层误差有差异,无法通过差分修正技术将对流层误差完全消除,导致差分修正残余对流层误差即非标称对流层误差的产生,而电离层误差可通过双频差分来消除,进而定位误差的主要来源为对流层[2]。
1994年,基于星基定位系统自动着陆的研究发现,异常对流层会导致系统定位失败[3]。2004年,研究发现0.2 m的差分修正残余误差会引起大约2.6 m的垂直保护级(Vertical Protection Level,VPL)增量[4]。2007年,Huang和van Graas研究发现,恶劣天气情况下,每6 km伪距有0.3 m对流层误差[5]。
后续的研究结果表明,对流层空间解相关误差为0.4 m/16 km[6]。2011年,van Graas和Zhu在研究对流层误差对GBAS影响中发现,对流层误差是导致定位失败的原因之一,需要深入研究[7]。综合上述研究得出结论:飞机与地面站之间的天气差异和水平距离会引入非标称对流层误差[8]。
为降低伪距修正残余误差引入的GBAS完好性风险,俄亥俄大学提出了包络非零均值误差的方法[4]。基于上述包络方法,法国民航大学相关研究分析了非标称对流层在单个静态点对GBAS的影响,但进近区和终端区动态飞行时,非标称对流层对GBAS的影响未知,且没有考虑卫星仰角和飞机与地面站之间距离的实时变化情况对非标称对流层误差的影响[9]。
针对上述问题,开展了非标称对流层误差对GBAS完好性的影响研究。首先,基于修正的Hopfield模型和“天气墙”模型,分析误差的影响因素,进而分析进近区和终端区的非标称对流层误差;其次,分析传统包络方法下非标称对流层误差对VPL的影响,进而评估其对GBAS完好性的影响;然后,综合考虑飞机与地面站之间距离、卫星仰角和天气情况对误差的影响,提出一种实时包络非标称对流层误差的方法(下文简称为实时包络方法),该方法需要地面站传输实时的气象数据,增多了VDB传输数据量; 最后,鉴于VDB传输带宽有限,为减少需要增加的VDB传输数据量,将实时计算的误差拟合为飞机与地面站距离和卫星仰角的函数,所得拟合结果为拟合包络方法。
1 非标称对流层误差 对流层误差分为垂直分量和水平分量,垂直分量即标称对流层,只与飞机与地面站之间的高度差有关,用现有的标称对流层误差修正方法计算[10];水平分量即非标称对流层误差,与飞机和地面站之间的水平距离及天气情况有关,由机载端和地面站根据实时天气情况和距离计算。
1.1 非标称对流层误差模型 非标称对流层误差模型如图 1所示,称之为“天气墙”模型[4]。图 1中,T0、P0和RH0为正常对流层下的温度、压强和相对湿度,Tw、Pw和RHw为非标称对流层下的温度、压强和相对湿度,D为飞机与地面站之间的距离,h0为飞机与地面之间的高度。“天气墙”模型表现了墙内外离散的天气情况。卫星信号穿过对流层顶端(标称对流层)时,经历的天气情况相同,不会产生非标称对流层误差;卫星信号通过路径1到达地面站时,经历的天气情况(温度、压强和相对湿度)与通过路径2到达机载端的信号不同,机载端和地面站基于修正的Hopfield模型计算的对流层误差有差异,导致非标称对流层误差产生, 相关研究发现,降雨量为1.5 cm/h,伪距误差为20 cm/km,说明降雨量是造成非标称对流层误差的主要因素[11]。
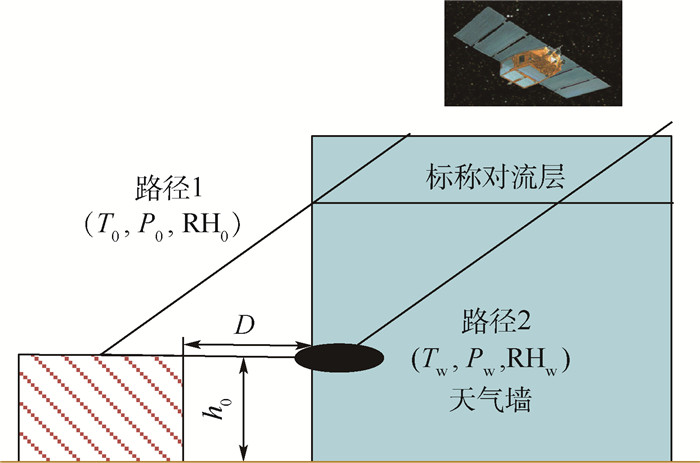 |
| 图 1 非标称对流层误差模型 Fig. 1 Non-nominal troposphere error model |
| 图选项 |
“天气墙”模型不包含对流层误差的垂直分量,同时,由于“天气墙”模型假设在整个仿真时间内,一直存在极端天气差异,因此有一定误差。
本文仿真中,天气情况设定如下:
1) 非标称气象天气情况(“天气墙”模型下层):Tw=26 ℃,Pw=102.325 kPa,RHw=100%,温度下降率为-6.5 K/km。
2) 标称气象天气情况(“天气墙”模型上层):T0=15 ℃,P0=102.325 kPa,RH0=50%, 温度下降率为-6.5 K/km。
1.2 影响非标称对流层误差的因素 图 2为飞机与地面站的距离为16和8 km时,基于修正的Hopfield模型计算的非标称对流层误差。
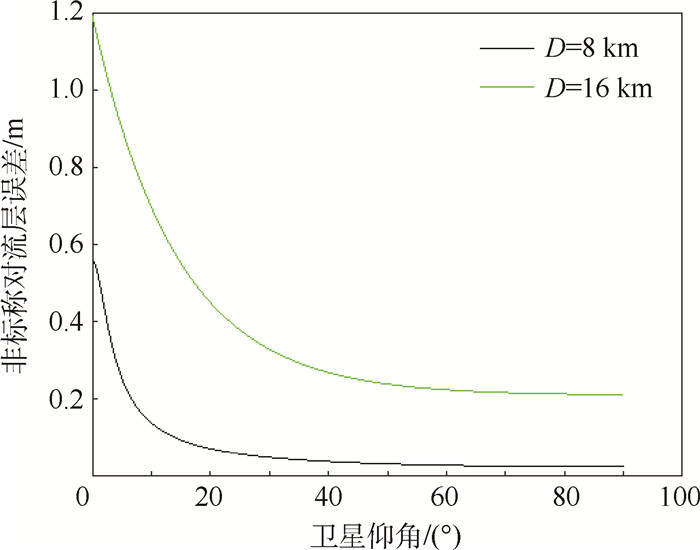 |
| 图 2 非标称对流层误差与卫星仰角之间的关系 Fig. 2 Relationship between non-nominal troposphere error and satellite elevation angle |
| 图选项 |
由图 2看出,飞机与地面站之间的距离越大,非标称对流层误差越大;卫星仰角越大,非标称对流层误差越小。
由上述分析可知,非标称对流层误差与飞机与地面站之间距离和卫星仰角有关,且进近过程中,卫星的仰角和飞机与地面站之间的距离时刻变化,图 3为飞机与地面站之间的距离为0~120km时,非标称对流层误差与卫星仰角之间的关系。
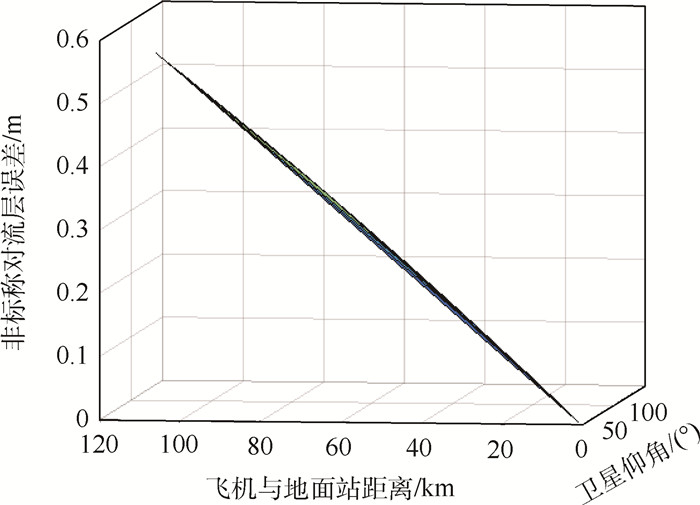 |
| 图 3 非标称对流层误差 Fig. 3 Non-nominal troposphere error |
| 图选项 |
由图 3看出,随着卫星仰角和飞机与地面站之间距离都增大时,非标称对流层误差呈增长趋势。
2 非标称对流层误差传统包络方法 2.1 方法流程 非标称对流层误差传统包络方法的处理流程如下[12]。
步骤1??记录相应区域一年的天气情况(温度、压强和相对湿度),计算每小时最大的天气变化量,并将其作为“天气墙”模型内外的天气差异值。
步骤2??将卫星仰角定为5°,机载端和地面站根据修正的Hopfield模型分别计算对流层误差,残余差分对流层误差即为非标称对流层误差。用绝对误差方法假设所有的卫星都对应最大的非标称对流层误差, 即[13]
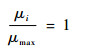 | (1) |
式中:μi为第i颗卫星对应的非标称对流层误差;μmax为所有卫星中最大的非标称对流层误差。
步骤3??计算非标称对流层标准差,即[4]
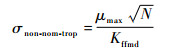 | (2) |
式中:N为可见卫星的数目;Kffmd为无故障漏检倍数。
步骤4??相关研究发现参数膨胀方法可最小化异常电离层对GBAS的影响,传统包络方法选用相对膨胀方法,将差分修正残余误差引入误差源标准差中[14]。非标称对流层下膨胀的垂直电离层梯度为[15]
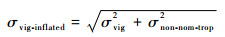 | (3) |
式中:σvig为垂直电离层梯度。
后续研究发现,传统包络方法适用于GBAS地面站,能够包络伪距修正残余对流层误差[16]。
步骤5??根据膨胀的垂直电离层梯度计算膨胀的电离层误差标准差σiono-inflated, i,以无故障状态H0为例,计算膨胀之后的误差源标准差为[10]
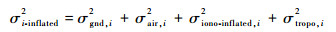 | (4) |
式中:σi-inflated为膨胀的误差源标准差;σgnd, i为伪距校正值误差标准差;σair, i为机载误差标准差;σiono-inflated, i为膨胀的电离层误差标准差;σtropo, i为对流层误差标准差。
步骤6??根据膨胀的误差源标准差,计算膨胀的VPL(即用户或机载端VPL)。VPL是评估GBAS性能的重要指标。VPL为以很大的概率(由完好性风险定义,完好性风险小于2×10-7)包络定位误差的置信边界[17]。以无故障状态H0为例,膨胀的VPL计算如下[14]:
 | (5) |
式中:Sv, i为第i颗卫星几何矩阵的垂直分量。
步骤7??计算非标称对流层下的理想VPL。理想的VPL可分为包络零均值高斯分布误差项VPLnon和包络伪距修正残余非零均值误差项VPLbias[13],即
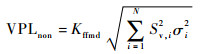 | (6) |
式中:σi为误差源标准差,即
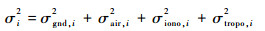 | (7) |
式中:σiono, i为标称对流层下的电离层误差标准差。
每一个误差源的非标称对流层误差由μi表示,则所有由非标称对流层误差引起VPL增量可表示为
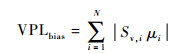 | (8) |
则理想的VPL可表示为
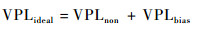 | (9) |
当VPLinflated≥VPLideal时,可以保障非标称对流层下GBAS的完好性,但传统的包络方法会引入部分完好性风险,下文通过分析非标称对流层误差的影响因素,进而提出改进方法,提高包络精度,降低包络方法引入的完好性风险。
2.2 传统包络方法下对GBAS完好性的影响 基于非标称对流层误差的影响因素,分析不同星座下,基于传统包络方法计算的非标称对流层误差对GBAS完好性的影响。
2.2.1 仿真条件 1) 天气情况设定如2.1节所述。
2) 滤波时间:100 s。
3) 星座:北斗区域性星座、北斗全球性星座、GPS标准星座和GPS当前星座。
4) 地点:林芝机场(E94.3°,N29.3°,2 949 m)。
5) 飞机速度:
GAST C(GBAS Approach Service Type C):77 m/s。
GAST D(GBAS Approach Service Type D):72 m/s。
6) 遮蔽角:5°。
7) 垂直告警限(VAL):如表 1所示[10], FASVAL为设定的初始告警限。
表 1 垂直告警限 Table 1 Vertical alert limit
| 垂直告警限 | H/m |
| FASVAL | H≤60.96 |
| 0.095965 H+FASVAL-5.85 | 60.96 < H≤408.432 |
| FASVAL+33.35 | H > 408.432 |
表选项
8) 仿真区域:单点:飞机高度为30 m和60 m;进近区:飞机高度60 m开始;终端区:飞机高度1 000 m开始。图 4为仿真区域示意图。
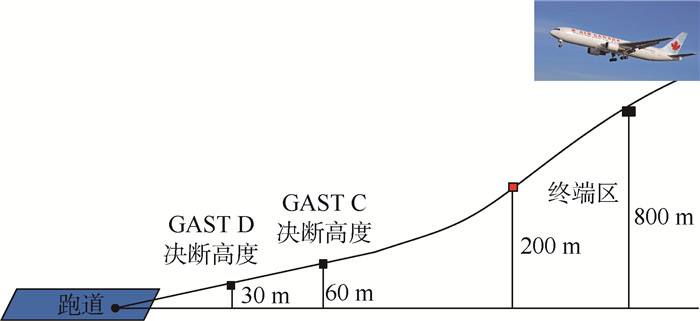 |
| 图 4 仿真区域 Fig. 4 Simulation regions |
| 图选项 |
2.2.2 仿真结果 下文仿真图中:黑线代表非标称对流层下理想的VPLideal;绿线代表不考虑非标称对流层误差时的VPLnon;紫线代表非标称对流层下膨胀的VPLinflated。
图 5为GPS当前星座下,不同时刻基于传统包络方法计算的非标称对流层误差对GBAS完好性的影响,图中:SV为可见卫星数。
 |
| 图 5 传统包络方法下VPL(GPS当前星座,GAST D) Fig. 5 VPL with traditional bounding method (current GPS constellation, GAST D) |
| 图选项 |
由图 5可以看出,设定告警限为10 m,传统包络方法下,VPLideal > VPLnon, 说明非标称对流层误差的引入增大了机载端VPL;且可见卫星数小于7时,VPLinflated高于告警限,说明传统的包络方法增大了非标称对流层误差和GBAS完好性风险,GPS GBAS的可用性受到影响。在单次进近过程中,一旦某一时刻VPL高于告警限,则导致该次进近过程不可用。由此可以推断非标称对流层误差可能给BDS GBAS引入完好性风险。
图 6为全球BDS星座下,基于传统包络方法计算的非标称对流层误差对GBAS完好性的影响。
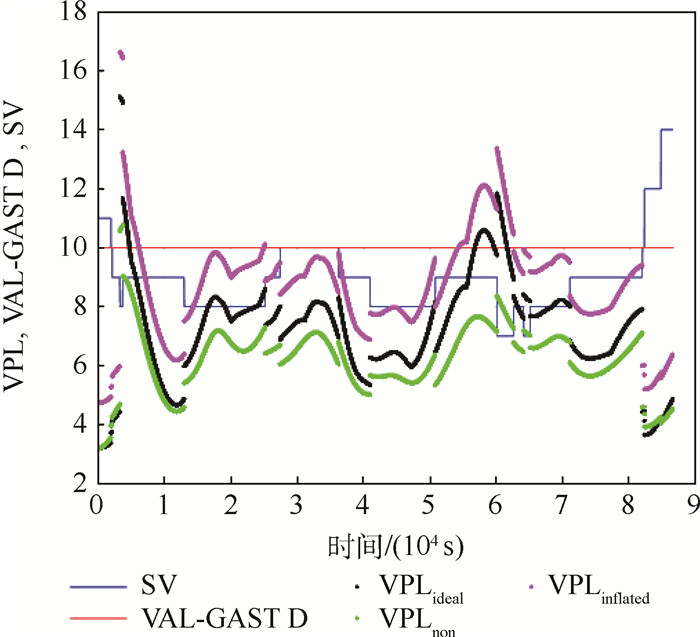 |
| 图 6 传统包络方法下VPL(全球BDS星座,GAST D) Fig. 6 VPL with traditional bounding method (global BDS constellation, GAST D) |
| 图选项 |
由图 6可以看出,传统包络方法下,VPLideal > VPLnon,结论与GPS星座下相同。
进近区域中,GBAS仅为一个机场的进场和离场飞行提供进近管制服务,而终端区内同时为2个或2个以上机场的进场和离场飞行提供管制服务,终端区范围较广,为减少对空中交通服务和航线运行的限制,应确保VPL和侧向保护级(Lateral Protection Level,LPL)符合相关标准规定。仿真也分析了终端区飞行时,非标称对流层误差的传统包络方法对VPL和LPL的影响。表 2为基于传统包络方法,不同星座在非标称对流层下,VPLinflated相对VPLideal的平均增量。
表 2 传统包络方法下保护级(PL)平均增量 Table 2 Average increase of protection level (PL) with traditional bounding method
| 星座 | 进近类型 | PL平均增量/m | ||
| 单点 | 单次进近 | 终端区 | ||
| 区域BDS | GAST C | 1.91 | 1.67 | 2.26(VPL) |
| GAST D | 1.79 | 1.73 | 2.17(LPL) | |
| 全球BDS | GAST C | 2.08 | 2.50 | 3.00(VPL) |
| GAST D | 1.09 | 1.72 | 1.80(LPL) | |
| 标准GPS | GAST C | 2.01 | 2.47 | 2.87(VPL) |
| GAST D | 1.51 | 1.86 | 1.95(LPL) | |
| 当前GPS | GAST C | 2.18 | 2.43 | 2.96(VPL) |
| GAST D | 2.09 | 2.52 | 2.94(LPL) | |
表选项
由表 2可知,传统的包络方法下,GAST C的平均VPL增量为2.36 m,GAST D的平均VPL增量为2.22 m,得出以下结论:传统包络方法增大了非标称对流层误差,增大了GBAS完好性风险,且非标称对流层误差对GAST C的影响大于GAST D;非标称对流层误差增大机载端VPL,GBAS完好性风险增大。
3 非标称对流层误差实时包络方法 由上述分析可知,传统的包络方法下,VPL增量最大为3 m,误差较大。进近过程中飞机与地面站之间的距离和天气情况,以及卫星的仰角时刻变化,非标称对流层误差也时刻变化,传统的包络方法不能基于实时卫星仰角和距离计算实时的非标称对流层误差,误差包络精度低,GBAS完好性风险增大。
鉴于上述问题,本文提出实时包络方法。根据实时的卫星仰角、飞机与地面站之间距离和周围的天气情况,机载端和地面站分别计算对流层误差,差分修正残余对流层误差即为该时刻、该颗可见卫星的非标称对流层误差。每一颗可见卫星都有其对应的非标称对流层误差μi,基于式(2) 计算每一颗可见卫星的非标称对流层误差标准差,进而计算每一时刻VPLideal和VPLinflated,具体计算流程如图 7所示。
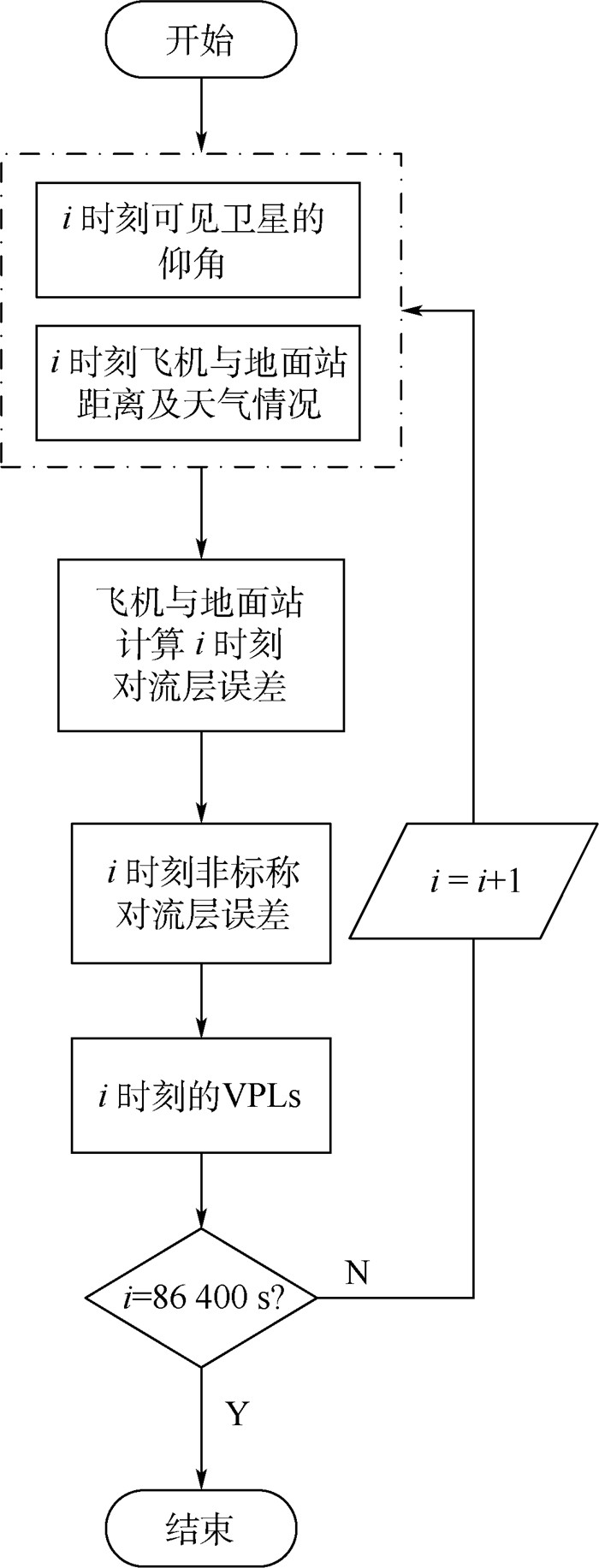 |
| 图 7 实时包络方法流程图 Fig. 7 Flowchart of real-time bounding method |
| 图选项 |
在相同的仿真条件下,基于实时包络方法,评估非标称对流层误差对GBAS完好性的影响。
下文仿真图中,蓝绿线代表实时包络方法下膨胀的VPLnew。
图 8为GPS当前星座下,基于实时包络方法计算的非标称对流层误差对GBAS完好性的影响。
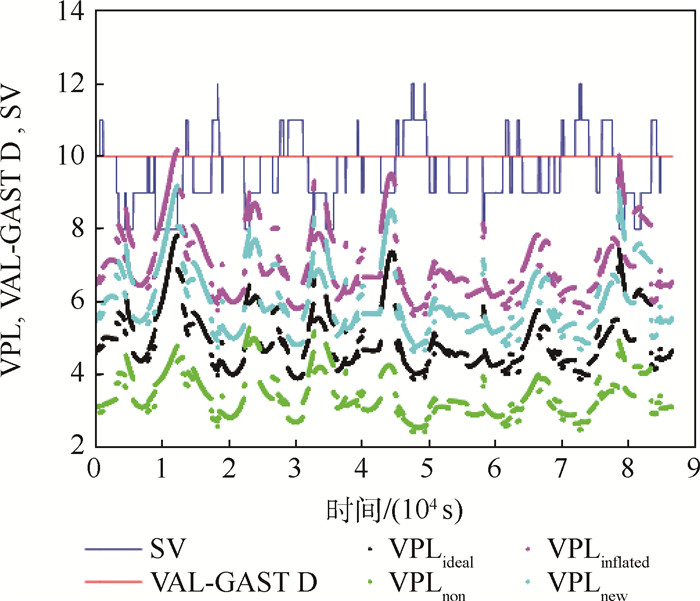 |
| 图 8 实时包络方法下VPL(GPS当前星座,GAST D) Fig. 8 VPL with real-time bounding method (current GPS constellation, GAST D) |
| 图选项 |
由图 8可以看出,GPS星座下,VPLnew < VPLinflated,说明实时包络方法提高了非标称对流层误差的包络精度,降低了GBAS的完好性风险,减少了系统的报警时间。
图 9为全球BDS星座下,基于实时的包络方法计算的非标称对流层误差对GBAS完好性的影响。
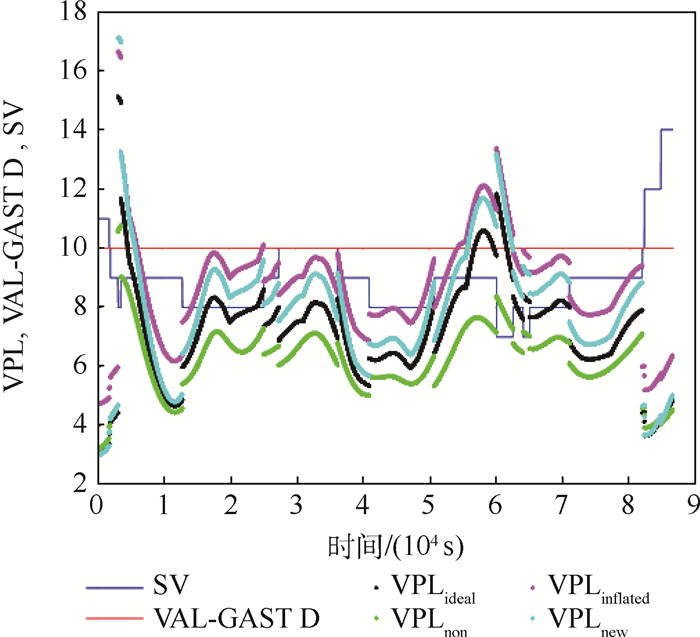 |
| 图 9 实时包络方法下VPL(全球BDS星座,GAST D) Fig. 9 VPL with real-time bounding method(global BDS constellation, GAST D) |
| 图选项 |
由图 9可以看出,全球BDS星座下,VPLnew < VPLinflated,结论与GPS星座下相同,验证了实时包络方法在BDS GBAS下的有效性。
表 3为基于实时包络方法,不同星座在非标称对流层下,VPLinflated相对VPLideal的平均增量。
表 3 实时包络方法下PL平均增量 Table 3 Average increase of PL with real-time bounding method
| 星座 | 进近类型 | PL平均增量/m | ||
| 单点 | 单次进近 | 终端区 | ||
| 区域BDS | GAST C | 1.42 | 1.33 | 1.63(VPL) |
| GAST D | 1.39 | 1.15 | 1.27(LPL) | |
| 全球BDS | GAST C | 1.64 | 1.60 | 2.04(VPL) |
| GAST D | 1.56 | 1.27 | 1.48(LPL) | |
| 标准GPS | GAST C | 1.71 | 1.62 | 1.99(VPL) |
| GAST D | 1.41 | 1.22 | 1.29(LPL) | |
| 当前GPS | GAST C | 1.81 | 1.66 | 1.96(VPL) |
| GAST D | 1.54 | 1.31 | 1.32(LPL) | |
表选项
实时包络方法下,与VPLideal相比,GAST C的平均VPL增量为1.75 m,GAST D的平均VPL增量为1.35 m,相比传统包络方法2.36 m和2.22 m的VPL增量,实时的包络方法减小了VPL增量,GAST C的包络精度提高了25.85%,GAST D的包络精度提高了39.19%。非标称对流层误差的实时包络方法减小了机载端VPL增量,降低了GBAS完好性风险,引入的包络误差减小。
表 4为不同星座下,与传统包络方法相比,实时包络方法提高的包络精度。
表 4 实时包络方法下包络精度平均提高量 Table 4 Average increase of bounding accuracy with real-time bounding method
| 星座 | 进近类型 | 包络精度平均提高量/% | ||
| 单点 | 单次进近 | 终端区 | ||
| 区域BDS | GAST C | 16.31 | 27.92 | 32.24(VPL) |
| GAST D | 28.40 | 36.90 | 40.32(LPL) | |
| 全球BDS | GAST C | 12.30 | 26.42 | 31.20(VPL) |
| GAST D | 34.60 | 36.39 | 40.42(LPL) | |
| 标准GPS | GAST C | 18.22 | 23.12 | 28.28(VPL) |
| GAST D | 35.30 | 40.80 | 35.52(LPL) | |
| 当前GPS | GAST C | 27.22 | 33.34 | 35.34(VPL) |
| GAST D | 40.41 | 45.31 | 55.20(LPL) | |
表选项
由表 4可知,实时包络方法下,包络精度平均提高32.52%,降低了非标称对流层误差包络方法给GBAS引入的完好性风险,验证了实时包络方法的有效性。
但实时包络方法降低VPL增量的同时,需要地面站给机载端传输实时的气象数据,机载端根据气象数据计算非标称对流层误差,这就增加了VDB传输数据。飞机进近过程中每秒需要传输的气象数据占412.28 B,3 298.24 bit所占带宽为3.22 bps。由VDB的传输带宽为31.5 kbps可知,传输气象数据时,将占用10.23%的VDB带宽,增大了VDB传输所需带宽。基于这一问题,下文提出减少VDB传输数据的拟合包络方法。
4 非标称对流层误差拟合包络方法 上述实时包络方法提高了非标称对流层误差包络精度,但增加了VDB数据传输量,鉴于VDB传输带宽有限,将图 3中离散误差样本点拟合为距离和卫星仰角的函数,拟合结果如下:
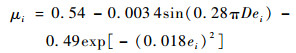 | (10) |
式中:ei为可见卫星仰角。
根据式(10) 的拟合结果,计算非标称对流层误差,进而评估拟合包络方法下非标称对流层误差对GBAS的完好性影响(见图 10)。由拟合结果可知,非标称对流层误差为飞机与地面站之间距离和卫星仰角的函数,机载端可根据距离和卫星仰角计算非标称对流层误差,地面站不需要播发实时的气象数据,减少了VDB传输负担。
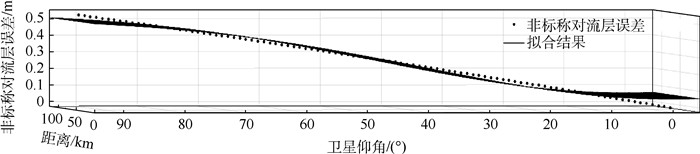 |
| 图 10 非标称对流层误差的拟合结果 Fig. 10 Fitting results of non-nominal troposphere error |
| 图选项 |
下文仿真图中,黄线代表拟合包络方法下膨胀的VPLnew1。
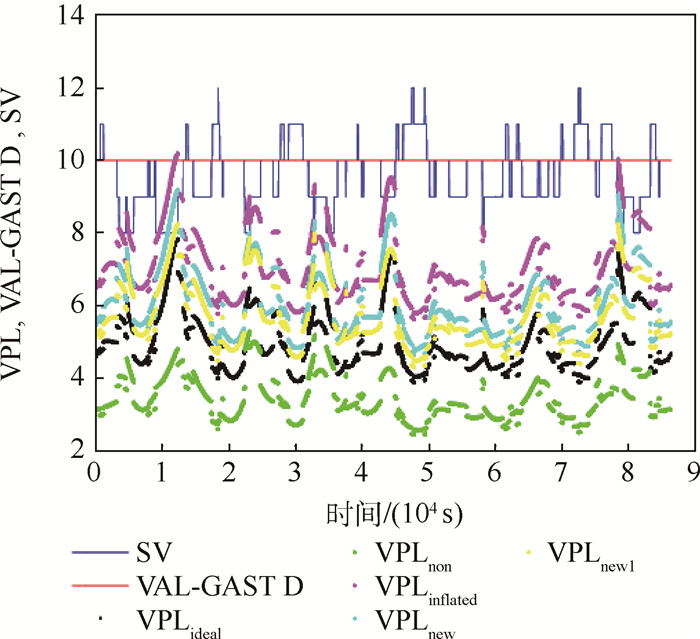
图 11为GPS当前星座下,基于拟合包络方法计算的非标称对流层误差对GBAS完好性的影响。
 |
| 图 11 拟合包络方法下VPL(GPS当前星座,GAST D) Fig. 11 VPL with fitting bounding method(current GPS constellation, GAST D) |
| 图选项 |
由图 11可以看出,GPS星座下,VPLnew1 < VPLnew,说明拟合包络方法在不需要增加VDB传输数据的同时,提高了非标称对流层误差的包络精度,降低了GBAS完好性风险。
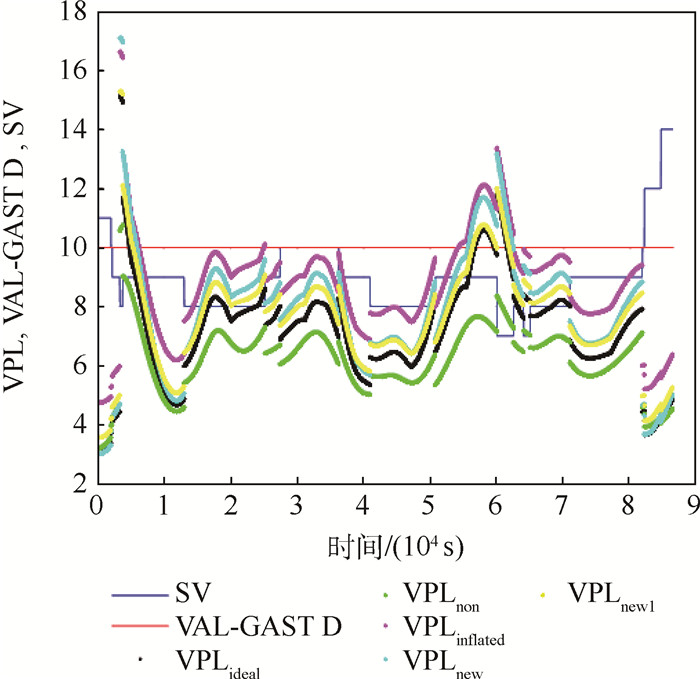
图 12为全球BDS星座下,基于拟合包络方法计算的非标称对流层误差对GBAS完好性的影响。
 |
| 图 12 拟合包络方法下VPL(全球BDS星座,GAST D) Fig. 12 VPL with fitting bounding method(global BDS constellation, GAST D) |
| 图选项 |
由图 12可以看出,拟合包络方法下,VPLnew1 < VPLnew,结论与GPS星座下相同,说明拟合包络方法提高了非标称对流层误差的包络精度,降低了GBAS完好性风险,验证了拟合包络方法在BDS GBAS下的有效性。
表 5为基于拟合包络方法,不同星座下,VPLnew1相对VPLideal的平均增量,代表拟合包络方法的误差。同样评估了拟合包络方法下,终端区飞行时非标称对流层误差对VPL和LPL的影响。
表 5 拟合包络方法下的PL平均增量 Table 5 Average increase of PL with fitting bounding method
| 星座 | 进近类型 | PL平均增量/m | ||
| 单点 | 单次进近 | 终端区 | ||
| 区域BDS | GAST C | 1.03 | 1.19 | 1.33(VPL) |
| GAST D | 0.85 | 1.07 | 1.14(LPL) | |
| 全球BDS | GAST C | 1.20 | 1.37 | 1.64(VPL) |
| GAST D | 1.07 | 1.26 | 1.28(LPL) | |
| 标准GPS | GAST C | 1.32 | 1.51 | 1.79(VPL) |
| GAST D | 1.01 | 1.09 | 1.21(LPL) | |
| 当前GPS | GAST C | 1.36 | 1.61 | 1.67(VPL) |
| GAST D | 1.01 | 1.12 | 1.34(LPL) | |
表选项
由表 5可知,拟合包络方法下,GAST C的平均VPL增量为1.42 m,GAST D的平均VPL增量为1.12 m,相比于实时包络方法下1.75 m和1.35 m的VPL增量,拟合包络方法减小了VPL增量,GAST C的包络精度提高了13.98%,GAST D的包络精度提高了10.36%,拟合包络方法减小了机载端VPL增量,降低了GBAS完好性风险,引入的包络误差减小。
表 6为不同星座下,与传统包络方法相比,拟合包络方法提高的包络精度。
表 6 拟合方法下包络精度平均提高量 Table 6 Average increase of bounding accuracy with fitting bounding method
| 星座 | 进近类型 | 包络精度平均提高量/% | ||
| 单点 | 单次进近 | 终端区 | ||
| 区域BDS | GAST C | 36.51 | 47.92 | 52.14(VPL) |
| GAST D | 34.40 | 42.90 | 47.32(LPL) | |
| 全球BDS | GAST C | 32.30 | 46.92 | 51.40(VPL) |
| GAST D | 40.60 | 43.50 | 46.52(LPL) | |
| 标准GPS | GAST C | 38.22 | 43.12 | 48.28(VPL) |
| GAST D | 41.30 | 47.80 | 42.52(LPL) | |
| 当前GPS | GAST C | 47.62 | 53.94 | 55.34(VPL) |
| GAST D | 46.80 | 53.70 | 60.20(LPL) | |
表选项
由表 6可知,在不同星座下,拟合方法在不需要增加VDB传输数据的同时,包络精度平均提高44.54%,降低了非标称对流层误差包络方法引入的GBAS完好性风险,验证了拟合方法的有效性。
5 结论 通过分析非标称对流层误差的影响因素,基于传统包络方法、实时包络方法和拟合包络方法,评估非标称对流层误差对GBAS完好性的影响,得出如下结论:
1) 与标称对流层下的VPL相比,非标称对流层下,GAST C的平均VPL增量为2.57 m,GAST D的平均VPL增量为2.01 m,说明非标称对流层误差增大了机载端VPL,增大了GBAS的完好性风险,且非标称对流层误差对GAST C的影响大于GAST D。
2) 基于传统包络方法,GPS当前星座下的平均VPL增量为2.52 m,标准星座下的平均VPL增量为2.12 m,区域BDS下的平均VPL增量为1.91 m,全球BDS下的平均VPL增量为2.20 m,说明传统方法下,随着可见卫星数目增大,非标称对流层误差越大,引入的GBAS完好性风险越大。
3) 与传统包络方法相比,采用本文实时包络方法,GAST C的包络精度提高了25.85%,GAST D的包络精度提高了39.19%。说明实时包络方法提高了非标称对流层误差的包络精度,降低了GBAS完好性风险。
4) 与实时包络方法相比,拟合包络方法下,GAST C平均VPL增量降低0.33 m,GAST D平均VPL增量降低0.23 m,包络精度平均提高了12.17%,说明拟合方法在不需要增加VDB传输数据的同时,降低了GBAS完好性风险,验证了拟合方法的有效性。
参考文献
| [1] | 李康, 巩冠峰. GPS地基增强系统简介及其性能仿真验证[J].电光与控制, 2013, 20(8): 89–94. LI K, GONG G F. Introduction of GPS ground based augmentation system and performance simulation[J].Electronics Optics & Control, 2013, 20(8): 89–94.(in Chinese) |
| [2] | SUPARTA W.Tropospheric modeling from GPS[M]//SUPARTA W, ALHASA K M.Modeling of tropospheric delays using ANFIS.Berlin:Springer International Publishing, 2016:19-52. |
| [3] | DIGGLE D W.An investigation into the use of satellite-based positioning systems for flight reference/autoland operations, dissertation[D].Columbus:Ohio University, 1994:2-17.http://rave.ohiolink.edu/etdc/view?acc_num=ohiou1173978322 |
| [4] | VAN GRAAS F, KRISHNAN V, SUDDAPALLI R, et al.Conspiring biases in the LAAS[C]//Proceedings of the Annual Meeting-Institute of Navigation.Manassas, VA:ION, 2004:300-307. |
| [5] | HUANG J, VAN GRAAS F. Comparison of tropospheric decorrelation errors in the presence of sever weather conditions in different areas and over different baseline lengths[J].Navigation, 2007, 54(3): 207–226.DOI:10.1002/navi.2007.54.issue-3 |
| [6] | HUANG J, VAN GRAAS F, COHENOUR C. Characterization of tropospheric spatial decorrelation errors over a 5-km baseline[J].Navigation, 2008, 55(1): 39–53.DOI:10.1002/navi.2008.55.issue-1 |
| [7] | VAN GRAAS F, ZHU Z.Tropospheric delay threats for the GBAS[C]//Proceedings of the International Technical Meeting of the Institute of Navigation.Manassas, VA:ION, 2011:959-964. |
| [8] | MATEUS P, NICO G, TOME R, et al. Experimental study on the atmospheric delay based on GPS, SAR interferometry, and numerical weather model data[J].IEEE Transactions on Geoscience & Remote Sensing, 2013, 51(1): 6–11. |
| [9] | GUILBERT A.Non-nominal troposphere reassessment for meeting CAT Ⅱ/Ⅲ with MC/MF GBAS[C]//Proceedings of the 28th International Technical Meeting of the Satellite Division of the Institute of Navigation.Manassas, VA:ION, 2015:1526-1537. |
| [10] | RTCA Inc.Minimum operational performance standards for GPS local area augmentation system airborne equipment:RTCA D0-253C-08[S].Washington, D.C.:RTCA, 2008:52.http://citeseer.uark.edu:8080/citeseerx/showciting;jsessionid=80FB1274FB7F1942290A0E9B45B1FB62?cid=8670408 |
| [11] | NILSSON T, B?HM J, WIJAYA D D, et al. Atmospheric effects in space geodesy[M].Berlin: Springer, 2013: 73-136. |
| [12] | SKIDMORE T, VAN GRASS F.An investigation of troposphere errors on differential GNSS accuracy and integrity[C]//Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation.Manassas, VA:ION, 2004:2752-2760. |
| [13] | RIFE J, PULLEN S. The impact of measurement biases on availability for CAT Ⅲ LAAS[J].Navigation, 2006, 52(4): 215–228. |
| [14] | SEO J, LEE J, PULLEN S, et al. Targeted parameter inflation within GBAS to minimize anomalous ionospheric impact[J].Journal of Aircraft, 2012, 49(2): 587–588.DOI:10.2514/1.C031601 |
| [15] | 李亮, 赵琳, 丁继成, 等. 提高LAAS空间信号可用性的完好性监测新膨胀算法[J].航空学报, 2011, 32(4): 664–671. LI L, ZHAO L, DING J C, et al. A new inflation integrity monitoring algorithm for improving availability of LAAS signal-in-space[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(4): 664–671.(in Chinese) |
| [16] | LEE J, PULLEN S, XIE G, et al.LAAS sigma-mean monitor analysis and failure-test verification[C]//Proceedings of Annual Meeting of the Institute of Navigation.Manassas, VA:ION, 2010:694-704. |
| [17] | ICAO NSP.GBAS CAT Ⅱ/Ⅲ development baseline SARP:Annex 10, Volume Ⅰ[R].Montreal:International Civil Aviation Organization, 2010. |
