传统的碳纤维导热性测量方法主要包括T形法[7]、3ω法[8-9]及直流通电法[10]等电学方法。这些方法测量原理简单、易于实现,但通常要求待测材料电阻和温度有明确的线性关系,限制了该方法应用。胡玉东等[11]利用激光拉曼测试方法,在333.15 K环境温度下测量了真空中单根碳纤维的热导率;Wang等[12]用激光拉曼方法测试了大气环境中直径为3.4 μm碳纤维的热导率。然而,碳纤维的导热系数与其微结构关系密切,碳纤维单丝间差异性直接导致导热性能测试结果的离散性偏大。
激光闪射法以其快速、准确的优点成为测试材料热导率最常用方法,已广泛用于复合材料导热性能表征,而将激光闪射法直接运用于碳纤维导热性能的测量尚无统一标准。何凤梅等[13]采用激光闪射法获得碳纤维热扩散率及导热系数,证实了激光闪射法测量碳纤维热扩散率的可行性,并研究了其热扩散率及导热系数随温度变化规律。Alway-Cooper等[14]根据激光闪射法原理提出了碳纤维复合材料沿碳纤维轴向热导率的有限元模型,并根据混合定律,基于碳纤维复合材料轴向热导率计算碳纤维轴向热导率。由此可见,进一步揭示纤维与树脂或空气介质间的相互影响,掌握试样结构参数对测试的影响,对实现激光闪射法准确表征碳纤维导热性能具有重要研究意义。
本文发展了碳纤维导热集束试样制备方法,研究了纤维体积分数、试样厚度、填充介质等因素对纤维导热测试的影响。在此基础上,分析了典型的聚丙烯腈基、中间相沥青基碳纤维的导热性能及其与结构关联规律。
1 实验 1.1 原材料 实验所用碳纤维包括日本石墨纤维公司的XN-90-60S沥青基碳纤维、日本东丽公司M55JB、以及国产T700、T800、M40J级碳纤维。所用树脂体系为江苏无锡树脂厂的环氧树脂E51与北京益利精细化工股份有限公司的三乙烯四胺固化剂。
1.2 实验方法 热扩散系数采用德国耐驰公司LFA-447激光闪射仪测试。测试过程中,激光源瞬间发射一束脉冲均匀照射在样品下表面,使用红外检测器连续测量样品上表面的温升过程,得到试样上表面半升温时间t1/2,即温升最大值的一半所需时间。根据Fourier传热方程可计算得到试样的热扩散系数为
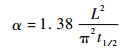 | (1) |
式中:L为试样厚度。导热系数K可由式(2) 计算得到:
 | (2) |
式中:C为比热容;ρ为密度。比热容采用梅特勒公司Q2000差热扫描量热仪测试。
纤维集束试样截面形貌采用JSM-7500型扫描电子显微镜观察,复合材料试样形貌采用金相显微镜观察。纤维结构参数采用D/max-2200型X射线衍射仪测试分析,选用Cu的Ka辐射,管压40 kV,管流40 mA,2θ的扫描范围5°~90°,扫描速度是6(°)/min。
1.3 导热试样制备方法 基于激光闪射仪工作原理,设计了可用于碳纤维集束热扩散系数测试的夹持器,克服了单根纤维导热差异性的影响。该集束夹持器由硬质聚氯乙烯制备而成,导热系数远小于碳纤维,不存在边缘效应。
碳纤维集束试样制备的关键是纤维体积分数与准直度控制。碳纤维集束夹持器直径为12.7 mm。依据目标体积分数Vf,通过式(3) 计算得到所需碳纤维集束的根数a。
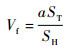 | (3) |
式中:ST为单束碳纤维截面积;SH为纤维夹持器截面积。试样制备过程中采用无水乙醇浸润碳纤维丝束以保证纤维的集束性,将纤维集束平行排放在夹持器内,确保纤维无打捻,夹紧后采用手术刀切除夹持器外的多余纤维,磨抛试样上下表面,以保证纤维端部平整,如图 1(a)所示。将试样放置于恒温鼓风干燥箱中50 ℃烘干至恒重。为观察纤维纵向分布,集束试样浸渍树脂后形貌如图 1(b)所示,纤维平行整齐排列且具有较高的准直度。
 |
| 图 1 用于导热系数测试的碳纤维集束试样及其复合材料形貌 Fig. 1 Morphology of carbon fiber bundle sample and its composite for thermal conductivity measurement |
| 图选项 |
同时,为对比直接测试碳纤维导热系数和基于复合材料间接测试分析纤维导热系数的差异性,实验制备了相同尺寸的单向复合材料试样。控制单向复合材料较低的孔隙率才能将其视为纤维和树脂基体双组元复合体系,本文中所制备单向复合材料孔隙率均低于1%,见图 1(c)。
2 结果与讨论 2.1 基于单向复合材料的碳纤维导热系数计算 纤维作为复合材料的重要增强体,其导热系数常通过测试复合材料导热性能,进而利用复合材料与组元材料导热系数的关系间接计算得到。如果将纤维增强复合材料热传导视为一维传热过程,则该复合材料导热系数与其组元材料导热系数通常用Landau-Lifshitz模型进行描述,即
 | (4) |
式中:K为导热系数,下标c、f和m分别代表复合材料、纤维与基体,n为结构常数,介于-1和1之间。作为铺层结构最简单的单向纤维增强复合材料,纤维平行排列,沿纤维方向传热时,式(4) 可简化为并联模型,即n=1时:
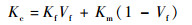 | (5) |
复合材料的导热系数可由式(2) 计算得到,其中热扩散系数由激光闪射仪测试,复合材料的密度ρc和比热容Cc可由式(6) 和式(7) 计算。
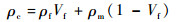 | (6) |
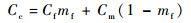 | (7) |
式中:mf为纤维的质量分数。将测试得到的复合材料导热系数代入式(5) 可进一步计算纤维的导热系数。
实验选用M40J级碳纤维,考察了纤维体积分数约为55%、60%和65%的复合材料的沿纤维方向的导热性能,测得的热扩散系数见图 2,纤维体积分数约55%的单向复合材料热扩散系数为24.7 mm2/s,随着纤维体积分数的增加,复合材料热扩散系数增加,纤维体积分数65%的单向复合材料热扩散系数为29.6 mm2/s。将热扩散系数、比热容和密度代入式(2) 计算得到复合材料导热系数,纤维体积分数55%、60%和65%时单向复合材料的导热系数为33.0、36.2和39.3 W/(m·K),表明随着纤维体积分数的增加,建立了更多的热传导路径。
 |
| 图 2 不同纤维体积分数和试样厚度单向复合材料热扩散系数与导热系数及计算的碳纤维导热系数 Fig. 2 Thermal diffusivity and conductivity of unidirectional composite and calculated thermal conductivity of carbon fiber under different fiber volume fraction and sample thickness |
| 图选项 |
复合材料导热系数代入式(4) 中,实验用树脂基体的导热系数为0.2 W/(m·K),由此计算得到纤维导热系数。纤维体积分数55%、60%和65%时对应的碳纤维导热系数计算值分别为58.3、59.1、60.4 W/(m·K),结果表明纤维体积分数影响碳纤维导热系数的间接测试结果。这主要因为与碳纤维相比树脂导热系数较小,热量沿碳纤维传递更快,极易发生沿碳纤维径向从碳纤维到树脂的热量传递,从而偏离一维的热传导模型,导致利用该方法计算得到的碳纤维导热系数高于其真值,而随着碳纤维体积分数增加,更多的碳纤维发生这种径向的热量传递,从而造成随着碳纤维体积分数增加,碳纤维导热系数计算结果呈增大趋势。
同时,实验对比分析了不同试样厚度对碳纤维体积分数的影响,制备了碳纤维体积分数约为60%的1 mm和4 mm厚试样,测试得到的复合材料热扩散系数、导热系数和计算得到的碳纤维导热系数如图 2(b)所示。随着试样厚度的增加,相应的热扩散系数和导热系数均略有增加,这与Alway-Cooper等[14]所制备的低碳纤维体积分数单向复合材料的结果变化趋势相一致。这主要因为测试中为避免漏光喷于表面的石墨材料延长了热传导过程,而随着试样厚度的增加,其影响逐渐减弱。
2.2 碳纤维集束试样导热系数计算 由于碳纤维与树脂间导热性能的差异,基于单向复合材料导热性能计算碳纤维导热系数时,极易受到沿碳纤维径向的热传导影响。为此,研究对比了无任何基体,利用碳纤维集束测试得到的碳纤维导热性。实验设计了碳纤维集束夹持器,碳纤维紧密堆积,依靠彼此间的摩擦作用形成完整的集束试样,因此,制备的试样纤维体积分数通常在60%~70%之间,试样最小厚度约为3 mm。由于空气介质室温导热系数仅为0.023 W/(m·K),密度仅为1.17 kg/m3,从碳纤维向空气介质传输的热量极为有限。因为空气介质密度低、集束试样中所占质量分数小,其对集束试样密度和比热容贡献可忽略,进一步将式(6) 和式(7) 代入式(2) 并忽略空气介质作用,则
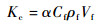 | (8) |
由于空气的导热系数极低,式(5) 忽略空气导热作用,并代入式(8),可得到碳纤维的导热系数为
 | (9) |
即采用碳纤维集束试样测试得到的热扩散系数直接反应了碳纤维的本征特性。
碳纤维体积分数和试样厚度是碳纤维集束试样的关键结构参数。为考察碳纤维体积分数对导热测试的影响,实验选用M40J级碳纤维制备了纤维体积分数为60%和65%的碳纤维集束试样,热扩散系数测试结果如图 3所示。与碳纤维复合材料不同,2个不同碳纤维体积分数试样的热扩散系数非常接近,约为40.0 mm2/s。这也证明了空气介质对碳纤维集束试样热传导的贡献极低,相比碳纤维,空气介质所传导的热量可忽略,同时沿碳纤维径向传递至空气介质的热量也极为有限,采用式(9) 计算碳纤维导热系数具有合理性。
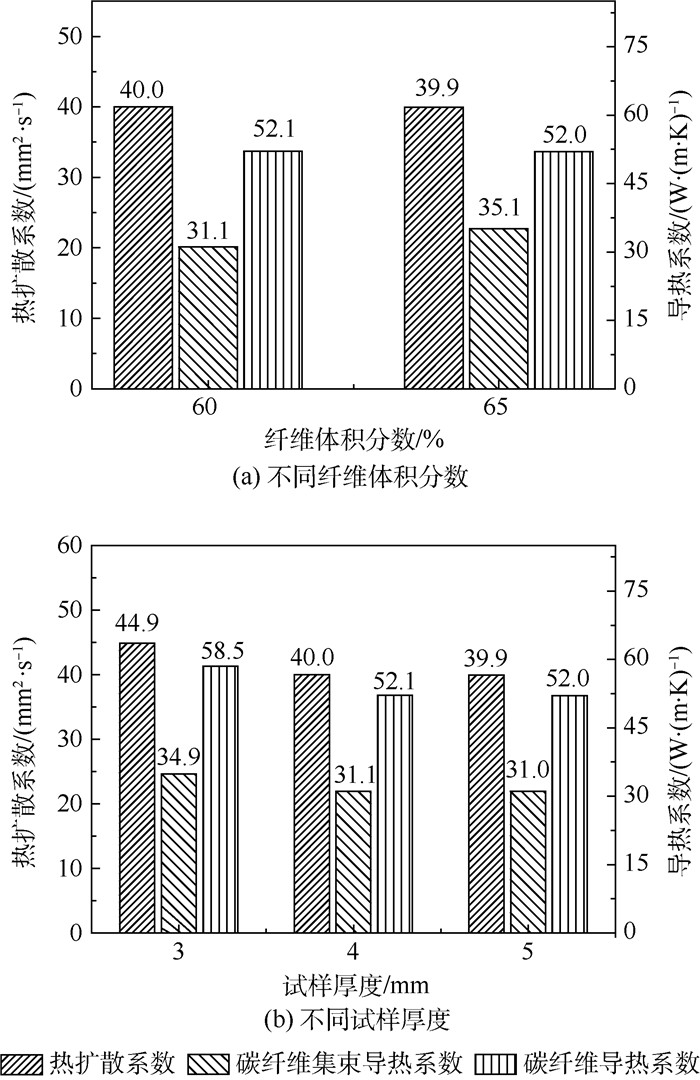 |
| 图 3 不同碳纤维体积分数和试样厚度碳纤维集束热扩散系数与导热系数及计算的碳纤维导热系数 Fig. 3 Thermal diffusivity and conductivity of fiber bundle and calculated thermal conductivity of carbon fiber under different fiber volume fraction and sample thickness |
| 图选项 |
将碳纤维的比热容为代入式(8) 和式(9),计算得到不同碳纤维体积分数下集束试样和碳纤维的导热系数测试值,见图 3。碳纤维集束试样的导热系数变化规律与单向复合材料一致,随着碳纤维体积分数的增加,表明沿热传导方向建立了更多热传导路径。在实验纤维体积分数范围内,计算得到的碳纤维导热系数均稳定在52.0 W/(m·K)左右,与基于单向复合材料计算得到的碳纤维热导率变化规律截然不同。这也证明低导热系数的空气介质有效抑制了沿着碳纤维径向的热传导,绝大部分热量均沿碳纤维轴向传递,因而碳纤维集束孔隙率的变化对碳纤维导热系数影响不大。
与相同碳纤维体积分数的单向复合材料对比,集束试样具有更高的热扩散系数,以碳纤维体积分数60%时为例,单向复合材料热扩散系数为27.1 mm2/s,而碳纤维集束热扩散系数高达40.0 mm2/s。单向复合材料与碳纤维集束试样上表面温升信号与时间典型曲线如图 4所示。由图可知,单向复合材料上表面采集的温升信号最高值明显高于碳纤维集束,这说明热量除了沿碳纤维进行传输外也通过树脂基体进行传递至上表面,从而试样上表面可监测到更高的温度。同时基于Cowan模型处理后[15],碳纤维集束比单向复合材料试样具有更低的半升温时间,表明碳纤维的热量传递并未完全沿着轴向,存在着碳纤维与树脂间的作用;而对于碳纤维集束试样,低导热系数的空气介质隔绝了热量沿着碳纤维径向传递,对上表面的温升信号几乎没有影响,热量集中沿着碳纤维集束传递。同时,对于碳纤维集束试样,随着碳纤维体积分数的增加,试样上表面的温升信号变大。分析表明,与基于单向复合材料间接计算碳纤维导热系数相比,碳纤维集束试样能够更准确地测得碳纤维轴向导热系数,且不受碳纤维体积分数影响。
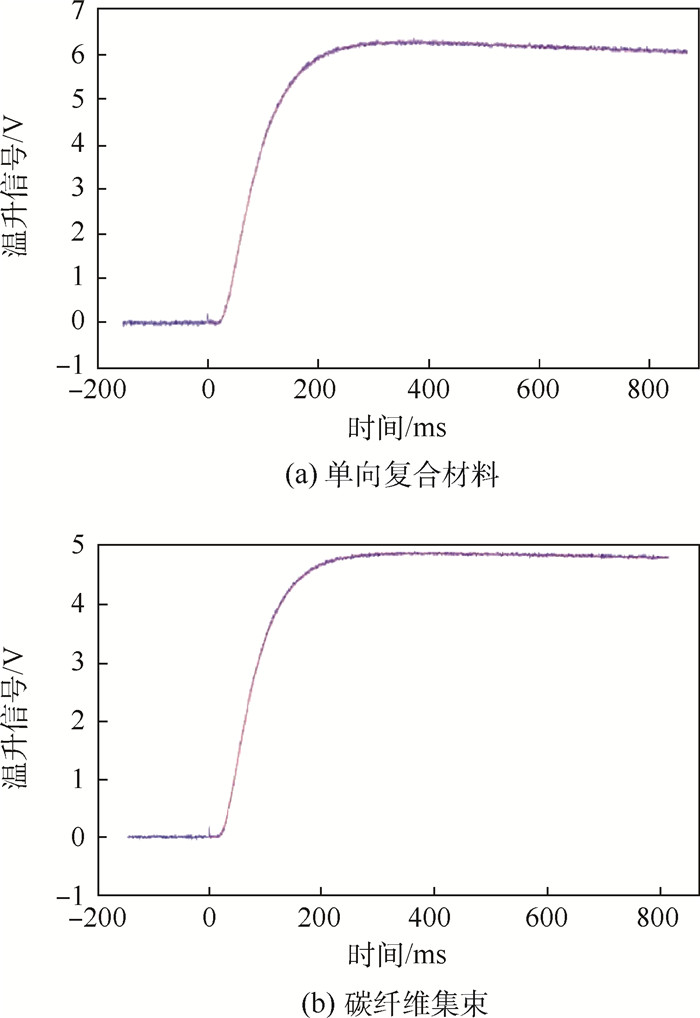 |
| 图 4 单向复合材料与碳纤维集束试样上表面温升信号与时间关系曲线 Fig. 4 Upper surface temperature rise signal versus time curves for unidirectional composite and carbon fiber bundle |
| 图选项 |
实验同时考察了碳纤维集束试样厚度对导热测试的影响。分别制备了试样厚度为3、4和5 mm的样品,碳纤维体积分数约为60%,其导热性结果见图 3(b)。3 mm厚的碳纤维集束试样热扩散系数为44.9 mm2/s,当试样厚度增至4 mm和5 mm,碳纤维集束热扩散系数稳定在40.0 mm2/s左右,计算得到的碳纤维导热系数约为52.0 W/(m·K)。这可能因为碳纤维集束试样存在较大的孔隙率,这些孔隙在试样底部的激光脉冲作用面可能存在一定的透光作用,试样厚度较小时,影响更大。因此采用碳纤维集束测试时应选用相对偏厚的样品。
此外,碳纤维集束的另一个重要参数是碳纤维准直度,随着碳纤维体积分数降低,局部碳纤维准直度可能降低。若碳纤维轴向与集束试样中心轴呈?角,则集束试样导热系数K?与碳纤维导热系数(轴向为Kx,纵向为Ky)关系可表示为[16]
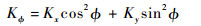 | (10) |
假设碳纤维轴向与试样轴向偏差一般不超过5°,由于碳纤维轴向导热系数远大于径向,忽略碳纤维径向导热系数贡献,由式(10) 测得的复合材料导热系数偏差不超过0.1%,表明采用碳纤维集束方法测试碳纤维导热系数的可靠性。
2.3 碳纤维导热性能与其结构关联性分析 实验采用碳纤维集束试样测试分析了典型的聚丙烯腈基、中间相沥青基碳纤维轴向导热系数,试样碳纤维体积分数均约为60%,测试结果见图 5。测得的T700、T800、M40J、M55J、XN-90-60S级碳纤维热扩散系数依次增加,分别为4.5、6.3、40.0、91.7和297.3 mm2/s,中间相沥青基碳纤维相对较高,高模型碳纤维次之,而高强型碳纤维热扩散系数相对偏低。计算得到的碳纤维导热系数呈现相同的变化规律,T700、T800、M40J、M55J、XN-90-60S级碳纤维导热系数分别为9.6、13.7、52.1、148.9和449.2 W/(m·K)。
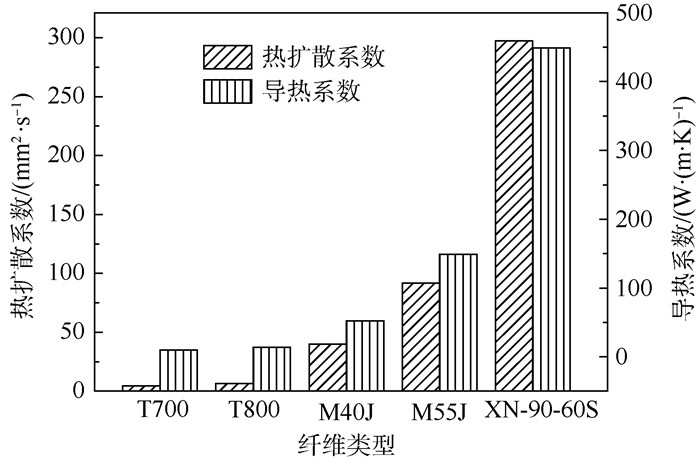 |
| 图 5 典型的聚丙烯腈基和中间相沥青基碳纤维的热扩散系数和导热系数 Fig. 5 Thermal diffusivity and thermal conductivity of typical PAN-based and mesophase pitch-based carbon fibers |
| 图选项 |
图 6为M55J和XN-90-60S碳纤维集束试样上表面温升信号与时间关系曲线,可以看出,M55J、XN-90-60S碳纤维半升温时间依次降低。同时在t=0时,2种碳纤维都出现了明显的信号峰,且沥青基碳纤维信号峰更为明显,这一现象在单向复合材料测试过程中表现出类似的曲线特征。
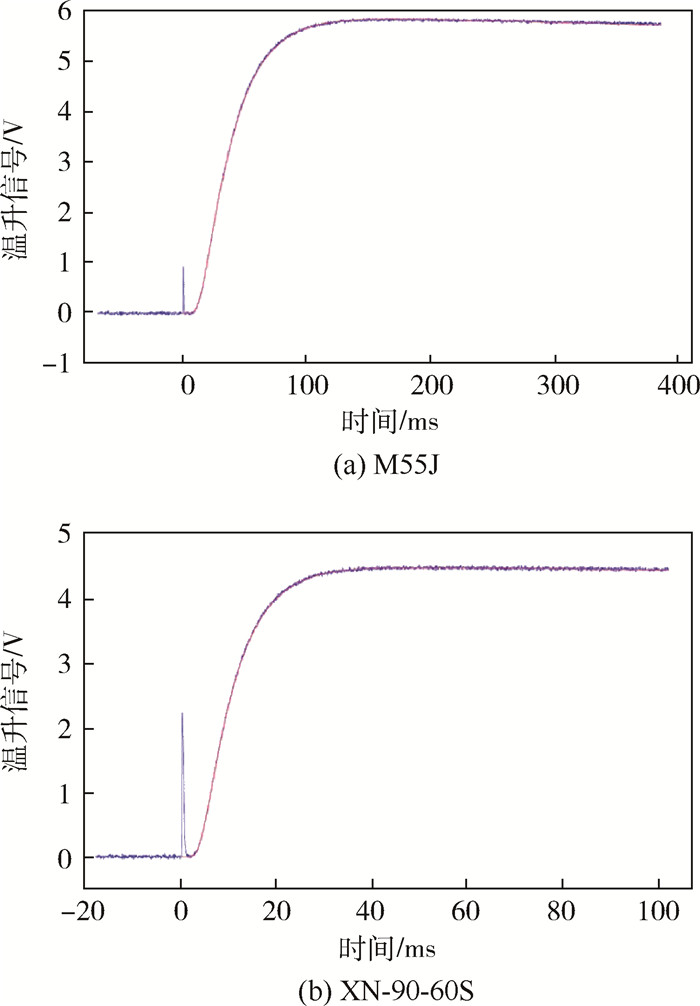 |
| 图 6 M55J和XN-90-60S碳纤维集束试样上表面温升信号与时间关系曲线 Fig. 6 Upper surface temperature rise signal versus time curves for M55J and XN-90-60S carbon fiber bundle |
| 图选项 |
同时,采用XRD分析了碳纤维的微观结构,结果如表 1所示。从高强型、高模型到中间相沥青基碳纤维,晶面间距d002逐渐减小,而晶粒大小总体上呈增大趋势,表明石墨化程度逐渐增加,XN-90-60S碳纤维的d002约为0.338 5 nm,而晶粒尺寸(Lc)高达14.83 nm,这也是中间相沥青基碳纤维横截面能够观察到清晰石墨晶粒的主要原因。碳纤维石墨化程度越高,晶面间距越小,晶粒尺寸越大,导热性能越好。
表 1 XRD测试的5种碳纤维微结构参数 Table 1 Microstructural parameters of five carbon fibers in XRD test
| 碳纤维类型 | d002/nm | Lc/nm |
| T700 | 0.3548 | 1.56 |
| T800 | 0.3473 | 1.91 |
| M40J | 0.3428 | 3.25 |
| M55J | 0.3424 | 8.31 |
| XN-90-60S | 0.3385 | 14.83 |
表选项
为揭示不同类型碳纤维导热差异性原因,实验观察了碳纤维截面形貌,见图 7。聚丙烯腈基碳纤维截面呈明显的颗粒状形貌,表明晶粒尺寸相对较小;而中间相沥青基碳纤维截面可观察到大尺寸的石墨微晶结构,并且石墨微晶沿着碳纤维轴向取向。导热过程是声子传递的过程,大尺寸晶粒及其沿碳纤维轴向高度取向的微结构均有利于声子沿碳纤维轴向传递,因此中间相沥青基碳纤维具有更高的导热系数。
 |
| 图 7 典型的聚丙烯腈基和中间相沥青基碳纤维截面形貌 Fig. 7 Cross-sectional morphology of typical PAN-based and mesophase pitch-based carbon fibers |
| 图选项 |
为验证本文的测试方法,制备了XN-90-60S沥青基碳纤维单向复合材料层板,中心采用功率5 W的热源加热,监测层板不同位置温度。同时根据本文方法测得的碳纤维导热系数,对复合材料层板温度场进行了模拟预报。结果表明,模拟与实验测试结果误差低于3 K,这也验证了该测试方法的准确性和可行性。
3 结论 对比分析了基于单向复合材料计算碳纤维导热系数和采用碳纤维集束测试导热系数的差异性与影响因素,得出如下结论:
1) 随着碳纤维体积分数增加,单向复合材料热扩散系数、导热系数增大;碳纤维体积分数越高、试样厚度越大,基于单向复合材料计算得到的碳纤维导热系数越大。单向复合材料试样比碳集束试样具有更低的热扩散系数;且受到碳纤维与树脂间热传导的影响,基于单向复合材料计算得到的碳纤维导热系数偏高。
2) 采用碳集束试样测试碳纤维导热系数时,碳纤维体积分数变化对碳纤维热扩散系数、导热系数测试结果影响不大。
3) 中间相沥青基碳纤维、高模型碳纤维、高强型碳纤维导热系数依次降低,晶面间距小、晶粒尺寸大,碳纤维导热系数越高。
参考文献
| [1] | DíAZáLVAREZ J, OLMEDO A, SANTIUSTE C, et al. Theoretical estimation of thermal effects in drilling of woven carbon fiber composite[J].Materials, 2014, 7(6): 4442–4454.DOI:10.3390/ma7064442 |
| [2] | DONG K, GU B, SUN B. Comparisons of thermal conductive behaviors of epoxy resin in unidirectional composite materials[J].Journal of Thermal Analysis & Calorimetry, 2015, 124(2): 1–15. |
| [3] | HAN S, CHUNG D D L. Increasing the through-thickness thermal conductivity of carbon fiber polymer-matrix composite by curing pressure increase and filler incorporation[J].Composites Science & Technology, 2011, 71(16): 1944–1952. |
| [4] | SCHUSTER J, HEIDER D, SHARP K, et al. Measuring and modeling the thermal conductivities of three-dimensionally woven fabric composites[J].Mechanics of Composite Materials, 2009, 45(2): 165–174.DOI:10.1007/s11029-009-9072-y |
| [5] | DONG K, LIU K, ZHANG Q, et al. Experimental and numerical analyses on the thermal conductive behaviors of carbon fiber/epoxy plain woven composites[J].International Journal of Heat & Mass Transfer, 2016, 102: 501–517. |
| [6] | VILLIèRE M, LECOINTE D, SOBOTKA V. Experimental determination and modeling of thermal conductivity tensor of carbon/epoxy composite[J].Composites Part A:Applied Science & Manufacturing, 2012, 504-506(46): 60–68. |
| [7] | ZHANG X, FUJIWARA S, FUJⅡ M. Measurements of thermal conductivity and electrical conductivity of a single carbon fiber[J].International Journal of Thermophysics, 2000, 21(4): 965–980.DOI:10.1023/A:1006674510648 |
| [8] | XIE S, LI W, PAN Z, et al. Mechanical and physical properties on carbon nanotube[J].Journal of Physics & Chemistry of Solids, 2000, 61(7): 1153–1158. |
| [9] | YI W, LU L, ZHANG D L, et al. Linear specific heat of carbon nanotubes[J].Physical Review B Condensed Matter, 1999, 59(14): R9015.DOI:10.1103/PhysRevB.59.R9015 |
| [10] | ZHANG X, XIE H, FUJⅡ M, et al. Thermal and electrical conductivity of a suspended platinum nanofilm[J].Applied Physics Letters, 2005, 86(17): 171912–1.DOI:10.1063/1.1921350 |
| [11] | 胡玉东, 刘锦辉, 王海东, 等. 拉曼方法同时测量单根碳纤维热物性和对流传热系数[J].化工学报, 2014, 65(S1): 251–257. HU Y D, LIU J H, WANG H D, et al. Simutaneous measurement of thermal properties and convective heat transfer coefficeient of individual carbon fiber using Raman spectroscopy[J].CIESC Journal, 2014, 65(S1): 251–257.(in Chinese) |
| [12] | WANG H D, LIU J H, ZHANG X, et al. Raman measurements of optical absorption and heat transfer coefficients of a single carbon fiber in atmosphere environment[J].International Journal of Heat & Mass Transfer, 2014, 70(2): 40–45. |
| [13] | 何凤梅, 李仲平, 冯志海, 等. PAN碳纤维高温热传输性能表征[J].中国材料进展, 2013, 32(4): 236–241. HE F M, LI Z P, FENG Z H, et al. Evaluation of thermal-transmission properties of PAN carbon fiber at hightemperature[J].Materials China, 2013, 32(4): 236–241.(in Chinese) |
| [14] | ALWAY-COOPER R M, THEODORE M, ANDERSON D P, et al. Transient heat flow in unidirectional fiber-polymer composites during laser flash analysis:Experimental measurements and finite element modeling[J].Journal of Composite Materials, 2012, 47(19): 2399–2411. |
| [15] | 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 闪光法测量热扩散系数或导热系数: GB/T 22588-2008[S]. 北京: 中国标准出版社, 2009: 9-10. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China.Determination of thermal diffusivity or thermal conductivity by the flash method:GB/T 22588-2008[S].Beijing:Standards Press of China, 2009:9-10(in Chinese). |
| [16] | PILLING M W, YATES B, BLACK M A, et al. The thermal conductivity of carbon fibre-reinforced composites[J].Journal of Materials Science, 1979, 14(6): 1326–1338.DOI:10.1007/BF00549304 |
