目前,国内外已针对高空风条件下的飞行仿真[1-2]、基于数字虚拟飞行的飞机操稳特性分析[3-5]等开展了研究工作,为本文的研究工作奠定了基础。文献[6-7]研究了飞机航线性能部分指标的计算方法;文献[8-11]采用工程估算方法研究了高空风对飞行的影响,但这些方法难以考虑高空风速和风向随空间位置变化、飞机航向变化、因配平高空风侧风分量而引起的阻力增加、飞行过程中的动态响应等因素的影响,因此难以精确计算高空风对飞机航线性能的量化影响。
针对上述问题,本文基于“驾驶员-飞机”闭环数字虚拟飞行仿真方法,研究建立了考虑高空风条件后飞机油耗、飞行距离、飞行时间等航线性能参数的计算方法。对算例飞机在高空风条件下的油耗和飞行时间等航线性能参数进行了分析,得出了高空风对大型客机航线性能的量化影响特点。
1 高空风模型 高空风随地理位置(Xg, Yg)、海拔高度H和飞行时间t发生变化。通常用风速大小Vw和风速方向Dw 2个参量来描述高空风,如式(1) 所示。其中,风速方向以真经线正北方向为0°,顺时针为正。
 | (1) |
通过查询气象数据,可以获取不同地区不同高度的高空风数据,包括高空风速大小和风速方向。如图 1所示为某时刻北京—昆明航线FL340(10 363.2 m)高度层上的风速大小和风速方向。图 1中,航段位置表示距离北京首都国际机场的航线距离。由图 1可以看出,该航线部分航段处的风速较大,最大可达到53.9 m/s。
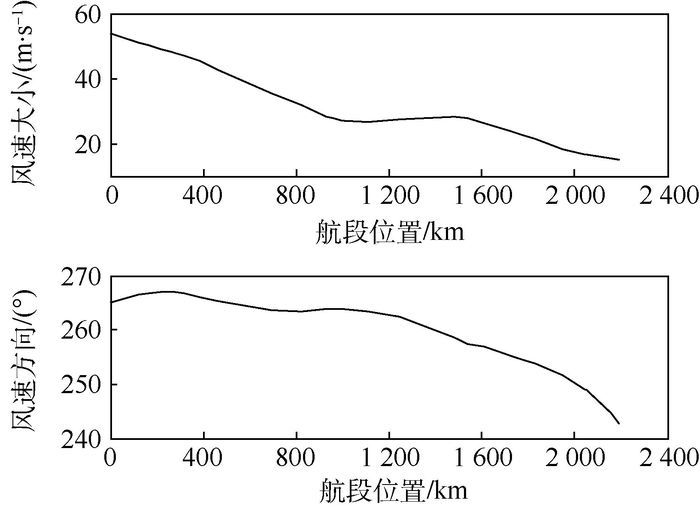 |
| 图 1 北京—昆明航线FL340高度层风速大小和方向 Fig. 1 Wind speed and direction of Beijing—Kunming route (FL340 height layer) |
| 图选项 |
为研究高空风对飞机飞行的影响,需根据高空风速大小Vw和方向Dw计算得到高空风速在地面坐标系[12-13]中的投影矢量[uwg vwg wwg]T,即
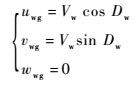 | (2) |
2 飞机飞行仿真模型 2.1 飞机飞行仿真模型结构 现代大型客机均采用了先进的飞行控制系统,在正常控制模式下,驾驶员的操纵指令经过飞行控制系统解算为飞机的执行器(包括操纵面和发动机等)指令,该指令通过舵机或发动机转化为飞机操纵面实际偏角或发动机推力,进而实现对飞机的操纵。因此,大型客机的飞行仿真模型包括飞行控制系统模型、执行器模型和飞机本体飞行动力学仿真模型,如图 2所示。
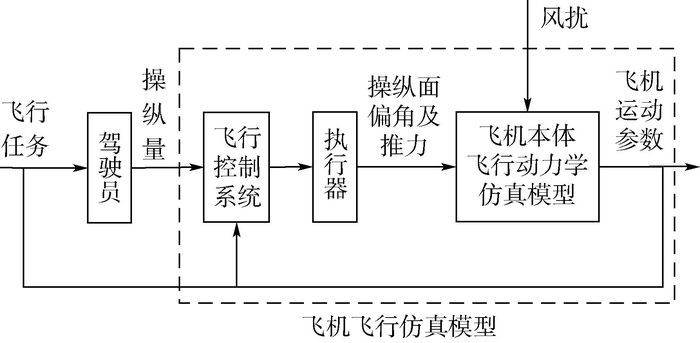 |
| 图 2 “驾驶员-飞机”闭环飞行仿真模型结构 Fig. 2 Structure of "pilot-aircraft" closed-loop flight simulation model |
| 图选项 |
不同型号客机的飞行控制系统模型不同,本文不做介绍。
2.2 飞机本体飞行动力学仿真模型
2.2.1 风场影响模型 有风时,飞机的空速矢量[u v w]T在机体坐标系中的投影矢量Vab为[12]
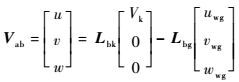 | (3) |
式中:Lbk为航迹坐标系到机体坐标系的坐标转换矩阵[12-13];Vk为飞机的航迹速度[12-13];Lbg为地面坐标系到机体坐标系的坐标转换矩阵[12-13];[uwg vwg wwg]T可由式(2) 计算得到。
飞机的空速Va、气动角α和β为[12]
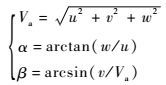 | (4) |
2.2.2 发动机油耗模型 飞机燃油的消耗速率dmF/dt为
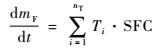 | (5) |
式中:mF为飞机燃油的重量,kg;nT为发动机的台数;Ti为飞机第i台发动机的推力,N;SFC为发动机的耗油率,kg/(kg推力·h)。
飞机的燃油消耗量(简称油耗)ΔmF为
 | (6) |
式中:tn为当前时刻。
飞机在飞行过程中的实际重量m为
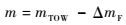 | (7) |
式中:mTOW为飞机的起飞重量,kg。
2.2.3 飞机本体飞行动力学仿真建模方法 根据飞机的气动、动力、重量等特性数据,由式(5) ~式(7) 可计算得到飞机的燃油消耗量ΔmF和实时重量m;将式(2) ~式(4) 计算得到的飞机在风场条件下的空速Va、气动角α和β,以及飞机的操纵面偏角代入飞机的气动数据可得到作用在飞机上的气动力和力矩。参照文献[4-5]的方法,可计算得到飞机在滑跑过程中地面对飞机的作用力和力矩。参照文献[12-13]给出的飞机六自由度飞行动力学和运动学方程,通过数值积分方法,可计算得到飞机的各飞行状态参数,包括飞机的飞行距离lR和飞行时间t,进而可对飞机的飞行和地面滑跑过程进行数学仿真模拟,并可得到飞机在风场条件下飞行时的油耗ΔmF、飞行距离lR和飞行时间t。
2.3 执行器模型 大型客机的执行器主要包括发动机和舵机。参照文献[3-4, 14],发动机推力与油门偏度之间的关系用一阶惯性环节来描述;操纵面实际偏角与舵机指令之间的关系也用一阶惯性环节来描述,并考虑操纵面偏转范围和偏转速率的限制。
3 驾驶员模型 驾驶员模型是用来模拟驾驶员对飞机操纵行为的数学模型。在大型客机的不同飞行阶段,驾驶员所需控制的目标参数不同,操纵策略不同,驾驶员模型的结构和参数也不同[3-5, 14-15]。
以飞机加速滑跑和起飞离地至安全高度的过程为例,该过程中驾驶员的操纵特点如下:① 发动机处于起飞推力状态,飞机从0 m/s开始加速滑跑;② 当飞机加速到抬前轮速度VR时,驾驶员拉杆使飞机抬头至期望的俯仰姿态角θc;③ 驾驶员操纵飞机的副翼和方向舵(前轮)用来纠正飞机在滑跑过程中和离地后的横航向偏离运动。根据驾驶员的这些操纵行为特点,可建立驾驶员模型的结构[3-5, 16],如图 3所示。图中:θ、φ和β分别为飞机的俯仰姿态角、滚转姿态角和侧滑角;θc、φc和βc分别为期望的俯仰姿态角、滚转姿态角和侧滑角;δp、δe、δa和δr分别为发动机油门偏度、升降舵偏角、副翼偏角和方向舵偏角;δp-TO为起飞推力状态的油门偏度;δec、δac和δrc分别为升降舵操纵通道操纵指令、副翼操纵通道操纵指令和方向舵操纵通道操纵指令;Gpθ(s)为δec对俯仰姿态角误差(θc-θ)的传递函数;Gpφ(s)为δac对滚转姿态角误差(φc-φ)的传递函数;Gpβ(s)为δrc对侧滑角误差(βc-β)的传递函数。
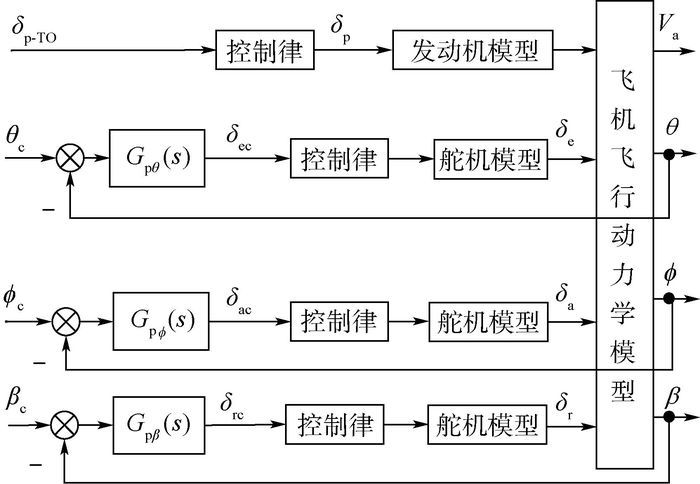 |
| 图 3 驾驶员模型结构 Fig. 3 Structure of pilot model |
| 图选项 |
在飞机加速滑跑和起飞离地至安全高度过程中,为使飞机尽快加速,发动机处于起飞推力状态。驾驶员油门操纵通道模型可由式(8) 表示:
 | (8) |
升降舵操纵通道中,当飞机的空速Va小于抬前轮速度VR时,升降舵操纵指令为0。当Va>VR时,驾驶员拉杆使飞机抬头至期望的俯仰姿态角θc,并在飞机爬升至安全高度前将俯仰姿态角θ保持为θc。θ对升降舵偏角δe的响应较快,驾驶员操纵的滞后时间对俯仰角响应的影响较为明显。传递函数Gpθ(s)选用能较好反映驾驶员操纵滞后的McRuer模型。因此,升降舵操纵通道模型可由式(9) 表示[3-5, 14]:
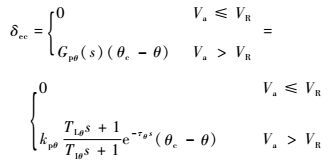 | (9) |
式中:kpθ为驾驶员增益;TLθ为驾驶员超前补偿时间常数;TIθ为驾驶员滞后补偿时间常数;τθ为驾驶员的反应及肌肉滞后时间。
副翼操纵通道模型可由式(10) 表示[3-5, 14]:
 | (10) |
式中:kpφ用来模拟驾驶员根据滚转角偏差(φc-φ)对副翼进行操纵的比例关系;e-τφs用来模拟驾驶员的反应延迟及肌肉滞后;kinφ/s用来模拟驾驶员根据(φc-φ)的积累对副翼进行操纵以减小φ的稳态误差的行为。
方向舵操纵通道中,驾驶员根据侧滑偏差(βc-β)对方向舵进行操纵。方向舵操纵通道模型如式(11) 所示[3-5, 14]:
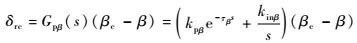 | (11) |
式中:kpβ表示驾驶员根据(βc-β)对方向舵进行操纵的比例关系;e-τβs表示驾驶员的反应延迟及肌肉滞后;kinβ/s用来模拟驾驶员根据(βc-β)的积累对方向舵进行操纵以减小稳态误差的行为。
与上述方法类似,可建立大型客机在航线飞行中其他各飞行阶段的驾驶员模型。
4 基于数字虚拟飞行的航线性能计算方法 在考虑高空风时,飞机的油耗、飞行距离、飞行时间等航线性能参数的计算步骤如下[3-5, 16]:
步骤1?制定飞行任务剖面。根据CCAR-121-R4[17]等民航规章要求,以及飞机的性能特点,制定飞机的飞行剖面,并确定装载燃油的重量。大型客机的典型飞行任务剖面、各飞行阶段的主要任务特点、备份油规则参见文献[18]。
步骤2?高空风建模。根据飞机航线所经历的位置,查询航路上的气象数据库或气象预报,得到给定航线上不同航段处的高空风速大小Vw和方向Dw。
步骤3?飞机飞行仿真建模。根据飞机的气动、动力、重量等数据,基于第2节方法,建立飞机在风场条件下的飞行动力学仿真模型。
步骤4?驾驶员建模。根据大型客机航线飞行任务剖面各飞行阶段的特点,基于第3节方法,分别建立各飞行阶段的驾驶员模型。
步骤5?人机闭环飞行仿真计算。利用已建立的飞机、驾驶员、高空风模型,建立高空风条件下的“驾驶员-飞机”闭环飞行仿真模型,如图 2所示。按照飞行剖面和给定航路,利用该人机闭环飞行仿真模型,对飞机的整个航线飞行过程进行数字仿真计算,得到飞机的油耗ΔmF、飞行距离lR和飞行时间t等状态参数。
步骤6?分析仿真计算结果得到航线性能参数。根据飞机在整个航线飞行过程中的人机闭环飞行仿真计算结果,飞机在飞行任务结束时的油耗ΔmF、飞行距离lR和飞行时间t即为飞机的航线油耗ΔmFR、航线飞行距离LR和航线飞行时间TR。
上述步骤[3-5, 16]可用图 4表示。
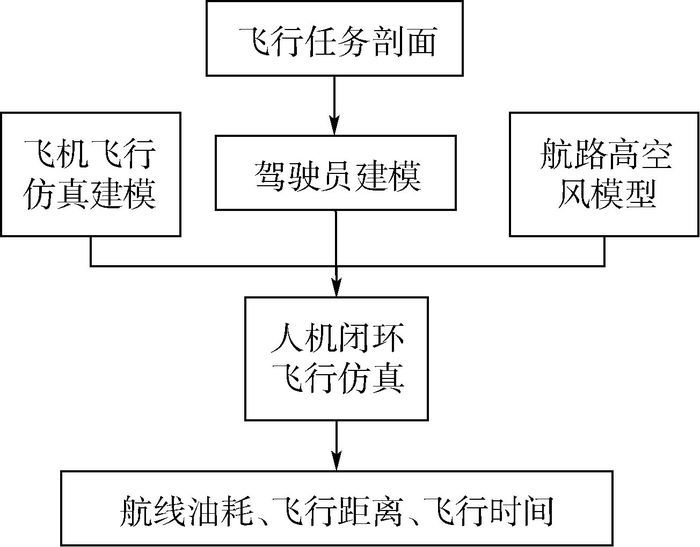 |
| 图 4 基于数字虚拟飞行的航线性能计算流程图 Fig. 4 Flowchart of route performance calculation based on digital virtual flight |
| 图选项 |
5 高空风条件下航线性能仿真计算实验 选取某型飞机作为算例,根据该型飞机的相关数据,可建立该型飞机在风场条件下的飞行动力学仿真模型。选定北京—昆明航线,根据CCAR-121-R4相关要求[17],制定飞机的飞行剖面。通过查询气象数据,得到该航线不同航段的高空风速矢量,如图 1所示。对算例飞机在该航线上的飞行进行数字仿真模拟计算,可以得出算例飞机各飞行参数随时间的变化曲线,如图 5所示。图中:t、χ、Uwind、Vwind分别为时间(以飞机起飞滑跑加速起始时刻为0 s)、航迹偏角、沿飞机航向的风速分量(正值表示顺风,负值表示逆风)、与飞机航向垂直方向的侧风速分量(正值表示侧风方向向右)。需要说明的是,由于高空风对飞机地面滑行时间和油耗的影响较小,本文仅考虑飞机从起飞滑跑到着陆滑跑结束之间的油耗和时间,不考虑地面滑行期间的油耗和时间。
 |
| 图 5 算例飞机执行北京—昆明航线飞行仿真结果 Fig. 5 Example aircraft flight simulation results on Beijing—Kunming route |
| 图选项 |
由图 5可以看出,飞机在执飞北京—昆明航线过程中,飞行距离LR为2 189 km,油耗ΔmFR为13 484 kg,飞行时间TR为145 min。由于整个航路中存在高空顺风,飞机的空速Va与航迹速度Vk并不相等。
由图 5还可看出,数字虚拟飞行方法考虑了高空风速(Uwind和Vwind)随空间位置的变化、飞机的航向χ和侧滑角β等飞行状态参数随时间的变化等因素,这些参数的变化均会引起气动力的变化,进而影响飞机的航线性能。工程估算方法计算航线性能时难以考虑这些因素。因此,采用数字虚拟飞行方法来计算飞机的航线性能时,相对工程估算方法可具有更好的精度。
同上方法可以计算得到,不考虑高空风时北京—昆明航线的油耗和飞行时间,以及在同一高空风场下(如图 1所示,飞行高度层为FL350(10 668 m)),算例飞机在执飞昆明—北京航线上的油耗和飞行时间,如表 1所示。此外,还可计算得到,在某高空风场条件下,算例飞机执飞北京—约翰内斯堡往返航线的油耗和飞行时间,如表 1所示。需说明的是,表 1中飞机在无风条件下执行往返航线飞行任务时的油耗和飞行时间略有不同,这是因为飞机起降机场的海拔高度不同,起飞爬升阶段和下降着陆阶段所需的时间和油耗不同。
表 1 算例飞机的部分航线性能计算结果 Table 1 Some route performance calculation results of example aircraft
| 航线 | 飞行距离/km | 油耗/kg | 飞行时间/min | ||
| 有风 | 无风 | 有风 | 无风 | ||
| 北京—昆明 | 2 189 | 13 484 | 14 501 | 145 | 156 |
| 昆明—北京 | 21 89 | 15 175 | 13 923 | 175 | 160 |
| 北京—约翰内斯堡 | 12 448 | 83 417 | 77 530 | 904 | 834 |
| 约翰内斯堡—北京 | 12 448 | 71 831 | 76 274 | 782 | 840 |
表选项
由表 1可以看出:
1) 在航线飞行时,高空风对飞机油耗和飞行时间的影响较大。
2) 在飞行距离相同时,顺风可以降低油耗,减少飞行时间,逆风会增加飞机的油耗,增加飞行时间。由于存在高空顺风,在飞行距离相同时,北京—昆明航线相对无高空风时的油耗减少7.0%(1 017 kg),飞行时间减少7.1%(11 min);由于存在高空逆风,昆明—北京航线相对无风时的油耗增加9.0%(1 252 kg),飞行时间增加9.4%(15 min)。这是因为大型客机在高空飞行时一般采用空速保持控制模式,遭遇逆风后,空速基本保持不变,地速减小,导致飞机飞抵目的机场的时间增加,油耗也增加;遭遇顺风时则飞行时间和油耗均减小。
3) 由于高空风的影响,同一航线往返飞行的油耗不同。北京与昆明往返航线上的油耗相差12.5%(1 691 kg),飞行时间相差20.7%(30 min);北京与约翰内斯堡往返航线上的油耗相差16.1%(11 586 kg),飞行时间相差15.6%(122 min)。
4) 在执飞远程航线时,由于航线距离接近飞机的设计航程,在逆风较多的航线上飞行时,需要飞机装载更多燃油,以确保飞机能够抵达目的机场。由于受到飞机最大起飞重量的限制,部分情况下,需要减小飞机的商载来装载更多的燃油。如北京—约翰内斯堡航线,需要减小算例飞机的商载才能装载足够燃油(包括83 417 kg航线油耗和备用油)。
6 结论 1) 提出了高空风条件下“驾驶员-飞机”闭环飞行仿真建模方法,基于数字虚拟飞行方法,提出了一套可考虑高空风影响的飞机航线性能计算方法。该方法可考虑高空风速和风向的变化、飞机航向变化、飞行中的动态响应等因素,计算结果较为准确可靠。
2) 高空风对大型客机航线飞行的油耗影响较大。在飞行距离相同时,顺风可以降低油耗,减少飞行时间,逆风会增加飞机的油耗,增加飞行时间。由于高空风的影响,同一航线往返飞行的油耗不同。
3) 在高空风较强的远程航线上,客机装载燃油时需要考虑高空风的影响。对于部分远程航线,由于高空风的影响,在满足最大起飞重量的限制下,飞机需要减小商载以装载更多燃油,确保能够飞抵目的机场。
4) 本文研究成果对于大型客机概念方案设计阶段的航线适应性分析具有一定的工程应用价值,并对于大型客机航线品质分析、飞行计划制定等工作具有一定的参考意义。
参考文献
| [1] | 严丽娟, 王丹霞, 陈楷民. 高空风影响下的线路飞行模拟算法[J].微计算机信息, 2009(4): 269–271. YAN L J, WANG D X, CHEN K M. Line flight simulation algorithm under the influence of high altitude wind[J].Microcomputer Information, 2009(4): 269–271.(in Chinese) |
| [2] | 李新胜, 杜冬, 李根军, 等. 高空风对飞行的影响在雷达模拟机中的建模和实现[J].中国民航飞行学院学报, 2004, 15(2): 28–31. LI X S, DU D, LI G J, et al. Modeling and implementation of high altitude wind impact on flight simulation in radar simulator[J].Journal of Civil Aviation Flight University of China, 2004, 15(2): 28–31.(in Chinese) |
| [3] | 贾重任, 黄成涛, 王立新. 空中最小操纵速度的人机闭环数学仿真计算[J].北京航空航天大学学报, 2013, 39(5): 580–584. JIA Z R, HUANG C T, WANG L X. Mathematical simulation method to calculate air minimum control speed[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(5): 580–584.(in Chinese) |
| [4] | HUANG C T, WANG L X, JIA Z R. A method to calculate the aircraft ground minimum control speed based on mathematical simulation[J].Procedia Engineering, 2011, 17: 24–38.DOI:10.1016/j.proeng.2011.10.004 |
| [5] | 刘海良, 王立新. 基于数字虚拟飞行的民用飞机纵向地面操稳特性评估[J].航空学报, 2015, 36(5): 1432–1441. LIU H L, WANG L X. Assessment of longitudinal ground stability and control for civil aircraft based on digital virtual flight test method[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1432–1441.(in Chinese) |
| [6] | EGBERT T. Cruise performance and range prediction reconsidered[J].Progress in Aerospace Science, 1997, 33(5-6): 285–321.DOI:10.1016/S0376-0421(96)00007-3 |
| [7] | BARTEL M, YOUNG T M. Simplified thrust and fuel consumption models for modern two-shaft turbofan engines[J].Journal of Aircraft, 2008, 45(4): 1450–1456.DOI:10.2514/1.35589 |
| [8] | DAMIáN R, OSCAR L G, SERGIO E, et al. An analysis of maximum range cruise including wind effects[J].Aerospace Science and Technology, 2014, 14(1): 38–48. |
| [9] | 丁立平. 分析计算高空风对飞行的影响[J].现代电子工程, 2005(3): 50–54. DING L P. Analysis and calculation of the effect of winds aloft on flight[J].Modern Electronic Engineering, 2005(3): 50–54.(in Chinese) |
| [10] | 赵鑫, 吕宗平, 张兆宁, 等. 自由飞行下考虑高空风的最小安全间距研究[J].航空计算技术, 2014, 44(3): 73–76. ZHAO X, LV Z P, ZHANG Z N, et al. Research on minimum safe distance in free flight considering winds aloft[J].Aeronautical Computing Technique, 2014, 44(3): 73–76.(in Chinese) |
| [11] | HALE F J, STEIGER A R. Effects of wind on aircraft cruise paerformance[J].Journal of Aircraft, 1981, 18(4): 320–321. |
| [12] | 肖业伦, 金长江. 大气扰动中飞行原理[M].北京: 国防工业出版社, 1993: 77-81. XIAO Y L, JIN C J. Flight principle in the atmospheric perturbation[M].Beijing: National Defense Industry Press, 1993: 77-81.(in Chinese) |
| [13] | 方振平, 陈万春, 张曙光. 航空飞行器飞行动力学[M].北京: 北京航空航天大学出版社, 2005: 174-186. FANG Z P, CHEN W C, ZHANG S G. Aircraft flight dynamics[M].Beijing: Beihang University Press, 2005: 174-186.(in Chinese) |
| [14] | 高浩, 朱培申, 高正红. 高等飞行动力学[M].北京: 国防工业出版社, 2004: 140-153, 222-223. GAO H, ZHU P S, GAO Z H. Advanced flight dynamics[M].Beijing: National Defense Industry Press, 2004: 140-153, 222-223.(in Chinese) |
| [15] | JOHNSON E N, PRITCHETT A R.Generric pilot and flight control model for use in simulation studies:AIAA-2002-4694[R].Reston:AIAA, 2002. |
| [16] | OHME P. A model-based approach to aircraft takeoff and landing performance assessment[C]//AIAA Atmospheric Flight Mechanics Conference.Reston:AIAA, 2009:6154. |
| [17] | 中国民用航空局. 大型飞机公共航空运输承运人运行合格审定规则: CCAR-121-R4[S]. 北京: 中国民用航空局, 2010. Civil Aviation Administration of China.Rules for the approval of the operation of large aircraft public air transport carriers:CCAR-121-R4[S].Beijing:Civil Aviation Administration of China, 2010(in Chinese). |
| [18] | 《飞机设计手册》总编委会.飞机设计手册第5册:民用飞机总体设计[M].北京:国防工业出版社, 2005:289-294. Aircraft Design Manual Editorial Board.Aircraft design manual.Fifth volume:Civil aircraft general design[M].Beijing:National Defense Industry Press, 2005:289-294(in Chinese). |
