日益广泛应用的锂离子电池(以下简称锂电池)潜在的安全问题成为制约其发展的一个瓶颈，主要体现在锂电池强放热反应使电池温度突然升高导致热失控，从而引发火灾、爆炸等严重事故。近年来发生的多起锂电池电动汽车自燃及航空运输锂电池火灾导致的货机坠毁事件引起全世界关注。国际民航组织(ICAO)基于现有飞机哈龙灭火系统不能有效地抑制锂电池火灾的现状，声明在锂电池运输风险得到缓解之前，禁止客机运输锂金属电池及单独运输的锂电池货物。以航空运输量较大的18650型锂离子电池为例，其单个包装件内包含100节锂电池，单次运输电池数量可达数千节，包装件内任何一电池意外起火传递给周围电池的热量都可能导致连续的热失控^[1-3]。锂电池热失控是指电池体系发生化学反应放出热量超过体系散失热量，体系温度自发升高的过程，锂电池热失控可导致电池燃烧爆炸。锂电池间热量传递现象可用多米诺效应解释，多米诺效应指在一个相互联系的系统中，一个很小的初始能量就可能产生一系列连锁反应的现象。当一节锂电池热失控后，其释放的能量在电池间传播，当突破热失控传播屏障后即发生灾害性的锂电池火灾事故^[4-5]。作为描述电池热失控特征的重要参数热释放速率(HRR)，单节锂电池热释放速率可用符合BS ISO 5660-1标准^[6]的小尺寸热释放速率实验装置基于氧消耗原理测得^[7-8]。以盒装100节18650型锂离子电池包装件为例，100节锂电池整体起火时火源放热符合一般规律，而当火灾始于单节锂电池热失控并逐步传播至其余锂电池时，热量释放既与单节电池热释放速率有关，又同热失控的传播过程有关。盒装18650型锂离子电池火灾为蔓延发展型时，整体热释放速率因电池有间隔的发生放热而呈现间歇性升高甚至降低。
国内外锂电池热失控的研究除美国联邦航空管理局开展为数不多的大尺度锂电池货物火灾实验外，以单节和少量锂电池的热失控及传播过程为主^[9-12]，大量锂电池火灾研究危险性和消耗大，采用火灾模拟研究可作为大尺寸锂电池火灾研究基础。准确的火源热释放速率是确保大量锂电池火灾模拟结果准确性的重要参数^[13]。蔓延发展型的锂电池火灾模拟应考虑到电池热失控传播和中断的过程。单节电池释放热量仅有部分用于加热临近电池，且锂电池电解液受热排气过程^[14-15]产生二氧化碳等产物影响热释放速率数值可靠性^[16]。本研究使用少量电池热失控实验与仿真模拟中电池表面温度变化对比后修正确定用于加热临近电池导致热失控传播的热量比例。通过小尺度实验和模拟相结合的方法，修正实验得到的标准热释放速率数据，获得影响锂电池热失控传播过程的等效热释放速率，用于需考虑热失控传播过程的锂电池火灾模拟。
1 锂电池热失控多米诺效应实验 1.1 实验平台及方案 18650型锂离子电池航空货物运输量大、应用广泛，以某品牌2600mA·h 18650型锂离子电池为对象，使用电加热装置触发电池热失控开展实验。实验平台包括厚壁防护容器、电池固定支架、直径为18mm的100W电加热棒、PID程序升温仪、K型热电偶及SIN-R5000D数据记录仪。使用8节18650型锂离子电池与加热棒3×3排列，实验平台结构及电池布置见图 1，电池排列编号0为加热棒，1~8为电池编号，8个热电偶分别紧贴各电池表面远离加热棒一侧。实验启动电加热棒缓慢加热至首个电池初爆，关闭加热装置，记录电池热失控发生顺序及各电池表面温度变化情况。

图 1 实验平台结构及电池排列示意图 Fig. 1 Schematic diagram of experimental platform structure and batteries arrangement

图选项

1.2 实验结果及多米诺效应分析 各电池表面热电偶温度，按照电池发生热失控顺序排列于图 2所示。

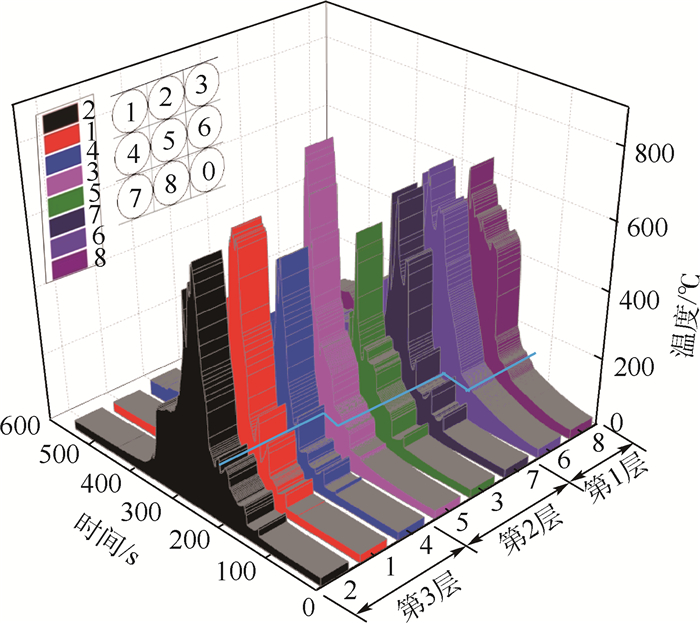图 2 实验电池温度变化曲线对比 Fig. 2 Comparison of temperature variation curves of experimental batteries

图选项

由图 2可知，18650型锂离子电池热失控可分为2个阶段，电池内部压力因化学反应升高至泄压帽开启压力后产生初爆，初爆时电池由顶端释放出高温烟气，若锂电池体系化学反应继续加速则相隔数十秒到数分钟后发生2次燃爆，燃爆后电池表面温度快速上升至最高温度。该18650型锂离子电池初爆温度约为180℃。3×3排列锂电池热失控初爆发生时间有显著阶段性，8号和6号锂电池距离加热棒最近，最早发生热失控且失控时刻接近，构成锂电池热失控多米诺传播过程第1层单元，随后相隔约40s后，7号、3号、5号电池相继发生初爆，构成锂电池热失控多米诺传播过程第2层单元，再过20s后，4号、1号、2号出现热失控，构成锂电池热失控多米诺传播过程第3层单元。锂电池热失控传播由第1层电池逐层向外传播。电池热失控传播过程处于同一层级相当位置的2节电池热失控发生时间存在差别，这是由于被加热电池受到局部高温，且加工工艺限制电池内部材料无法达到绝对均匀，因此可因个体差别导致热失控顺序在小范围内体现出随机性，整体保持层级传播的规律性，当上一层级发生热失控时，相邻下一层级电池平均温度相差约100℃。
锂电池热失控极易传播，实验条件下停止加热棒供电后热失控依然在锂电池间持续传播直至所有电池陷于火海。当前控制锂电池火灾的公认方法是降低电池温度阻止热失控传播。由于18650型锂电池体积小燃烧反应历时短，降低反应体系温度对中断已发生燃烧的锂电池效果不显著，但降低温度可阻止临近电池温度的危险升高从而阻断热失控在锂电池之间的传播。大量锂电池火灾模拟应充分考虑锂电池火源因热失控传播或传播中断而导致的热释放速率间歇性升高或降低。锂电池热失控传递热量主要来源于电池之间的热传导^[17-19]，且锂电池热释放速率一部分用于加热其他锂电池，另一部分随燃烧烟气流动而散失。电池热失控放出热量导致热失控传递的部分可由少量相同电池的热失控传播实验和仿真对比分析得出，从而用于模拟更大数量相同锂电池的大规模火灾发展和控制过程。
2 基于标准锂电池热释放速率的热失控仿真 2.1 仿真模型及参数设置 利用FLUENT建立的18650型锂电池空运包装件热传递的有限元模型为

(1)

式中：ρ为电池密度，kg/m³；c_p为比热容，J/(kg·K)；T为温度，K；t为时间，s；λ为导热系数，W/(m·K)；Q为电池内部的热释放速率对应的热生成率，W/m³。
模型中考虑电池之间和紧邻电池的一薄层空气的传热，不考虑电池喷出烟气燃烧火焰的热辐射及对流传热作用。锂电池体系化学反应过程复杂^[20]，难以精确模拟化学反应过程放热，采用实验的放热数据作为电池放热引发热失控传播的能量参照更为可行。使用相同材料和状态的18650型锂离子电池，实验中热释放速率曲线简化后作为实验中加热棒代表的初始热失控电池放热过程。仿真中锂电池使用均一化参数，轴、径向导热系数分别为14和3.4 W/(m·K)，平均密度2 580 kg/m³，平均比热830 J/(kg·K)。根据实验现象以180 ℃作为电池热失控起始温度，初始热失控电池在仿真开始时即使用UDF(User Defined Function)功能加入放热源。其他电池以表面温度达到热失控起始温度为判据加入放热源，记录各电池温度变化。网格数量为14 752，所有网格的Warpage值 < 10、Jacobian值 > 0.5，该网格质量符合要求。
为验证模型网格无关性，以恒定放热功率为热源，划分不同尺寸网格对比模型最高温度随时间的变化结果，数据对比见表 1。
表 1 不同网格数量下温度随时间变化 Table 1 Temperature changes over time under different numbers of grid

网格数量	温度/K
	t=25s	t=50s	t=100s	t=150s	t=200s
14 752	408	505	670	788	862
100 740	405	504	672	784	869
224 268	404	502	677	784	863

表选项






由表 1中数据对比可知，最高温度随时间变化情况随网格数量变化很小，相对误差在1%以内，因此采用14 752网格数量可以满足计算精度的要求。
2.2 仿真结果分析 图 3为某时刻电池温度分布云图。仿真温度分布结果可见热失控传播过程层级之间电池表面的温度存在约100℃温差，与实验现象一致。将仿真和实验中各电池热失控起始温度、达到最高温度时间、最高温度值汇总于表 2所示。

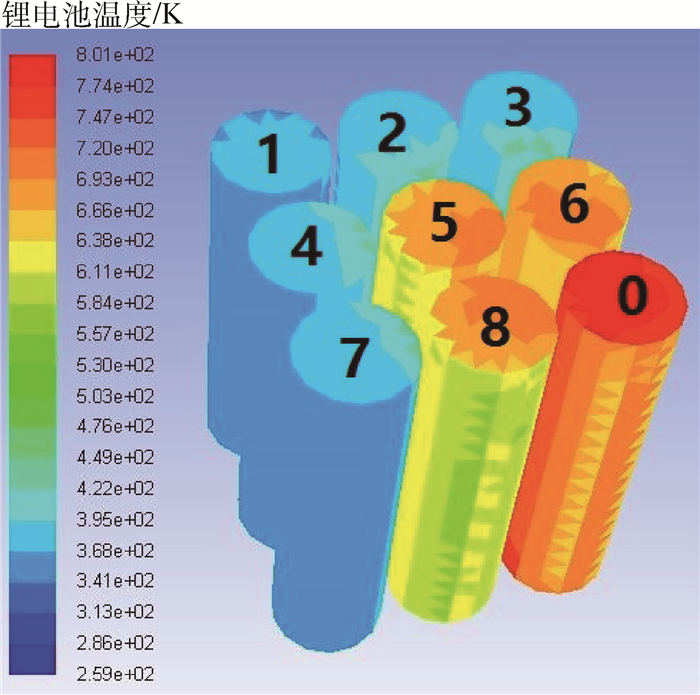图 3 仿真3×3锂电池温度分布 Fig. 3 Temperature distribution of 3×3 lithium battery

图选项

表 2 各节电池表面温度参数的实验与仿真结果对比 Table 2 Comparison of experimental and simulation results of temperature parameters of cell surface

电池编号	初爆时间/s		达到最高温度时间/s		最高温度/℃
	实验	仿真	实验	仿真	实验	仿真
8	160	95	231	160	652.6	1 386.4
6	170	95	245	160	681.4	1 386.4
7	196	125	244	144	656.7	1 311.5
3	199	125	243	144	593.6	1 311.5
5	209	115	254	158	846.5	1 701.9
4	218	130	250	166	620.5	1 322.7
1	218	138	261	176	737.1	1 459.3
2	218	130	259	166	699.4	1 322.7

表选项






由表 2数据对比可知电池表面最高温度仿真结果显著高于实测温度，且仿真得到的电池热失控发生时间和达到最高温度的时间提前。出现该情况原因在于电池燃烧释放热量并非全部用于加热临近电池，多数热量由热失控时喷出到环境中的易燃气体燃烧释放并随烟气散失，因此需修正实验得到的热释放速率以降低此种仿真误差。
3 基于二分法的锂电池热释放速率等效修正 为分析电池释放热量中加热临近电池的热量比例，采用二分法逐次对热释放速率曲线进行修正。二分法又称半分法，是一种方程根的近似求解方法，通过每次把方程根所在小区间收缩一半的方法，使区间的2个端点逐步迫近函数的零点，以求得零点的近似值。依据二分法基本思想，以实验温度曲线为目标，对比初次仿真结果将热释放速率曲线节点功率减半，代入计算后根据结果比较再次增减，使仿真温度结果不断逼近实验温度曲线。采用二分法逼近实验温度曲线所得热释放速率即为锂电池在热失控过程中用于多米诺效应热传递的修正后的热释放速率。
因实验中电池表面热电偶温度可受到相邻电池热失控火焰影响，所以选择实验中接近加热棒外侧7号电池表面热电偶测温位置温度曲线作为修正目标。修正前后热释放速率曲线及锂电池7的温度对比分别如图 4和图 5所示。修正后锂电池7的表面温度与试验温度一致性较高。

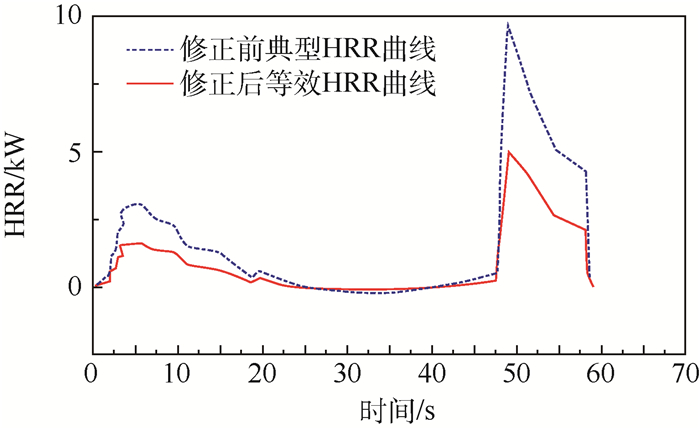图 4 修正前后热释放速率(HRR)曲线对比 Fig. 4 Comparison of heat release rate(HRR) curves before and after correction

图选项

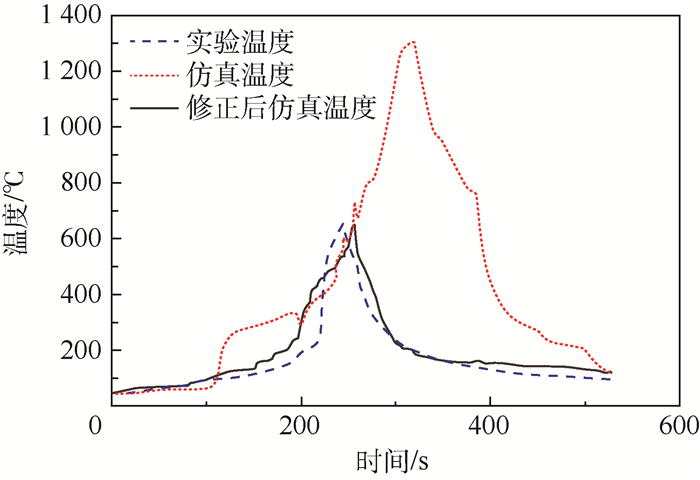图 5 锂电池7的温度曲线对比 Fig. 5 Comparison of temperature curves of lithium battery 7

图选项

使用修正后的热释放速率曲线再次进行3×3排列仿真，对比各电池表面温度与实验数据如表 3所示。
表 3 各节电池表面温度参数的实验与修正后仿真结果对比 Table 3 Comparison of experimental and simulation after correction results of temperature parameters of cell surface

电池编号	初爆时间/s		达到最高温度时间/s		最高温度/℃
	实验	仿真	实验	仿真	实验	仿真
8	160	175	231	233	652.6	679.5
6	170	175	245	233	681.4	679.5
7	196	204	244	256	656.7	652.6
3	199	204	243	256	593.6	652.6
5	209	198	254	257	846.5	849.1
4	218	217	250	252	620.5	684.5
1	218	221	261	260	737.1	716.4
2	218	217	259	252	699.4	684.5

表选项






由表 3可知，采用针对一节电池温度修正后得到等效热释放速率应用于整体仿真时，各电池初爆时间、达到最高温度时间、最高温度与实验数据基本吻合，且误差没有随着热失控传播扩大的趋势。可将该方法扩展到更多数量锂电池的热失控场景研究。
4 结论 1) 锂电池热失控传播具有显著多米诺效应，3×3排列锂电池热失控传播展示出3层级的热失控传播，各层级间热失控发生时间接近并与下一层级存在一定时间间隔。虽然单节锂电池热失控发生后控制难度大，但切断电池热失控在层级之间的传播，增加层级间热传递间隔可提高险情被发现的概率和延长控制的时间，可用于指导现有锂电池包装件防火设计。
2) 由于锂电池燃烧热量仅部分用于加热临近电池导致热失控传播，利用单节18650型锂离子电池典型热释放速率曲线仿真热失控在锂电池传播过程得到温度和时间特征与实验差别较大。修正得到的锂电池热释放速率等效曲线用于18650型锂离子电池热失控传播仿真可准确表现实验过程中热失控的多米诺现象和电池表面温度变化情况，可推广应用于各种型号及不同数量锂电池火灾仿真研究。
3) 基于标准的单节18650型锂离子电池典型热释放速率曲线通过实验和仿真方法得到的等效热释放速率曲线，其用于模拟电池火灾的准确性还有待大尺度锂电池火灾实验数据的验证，且应考虑锂电池火源其余热量在模型中的加入方式确保火源能量释放总量与实际相符。

参考文献

[1]	WEBSTER H.Fire protection for the shipment of lithium batteries in aircraft cargo compartments:DOT/FAA/AR-09/55[R]. Washington, D.C.:Federal Aviation Administration, 2010:1-4.
[2]	FENG X, SUN J, OUYANG M, et al. Characterization of penetration induced thermal runaway propagation process within a large format lithium ion battery module[J].Journal of Power Sources, 2015, 275: 261–273.DOI:10.1016/j.jpowsour.2014.11.017
[3]	SPINNER N S, FIELD C R, HAMMOND M H, et al. Physical and chemical analysis of lithium-ion battery cell-to-cell failure events inside custom fire chamber[J].Journal of Power Sources, 2015, 279: 713–721.DOI:10.1016/j.jpowsour.2015.01.068
[4]	罗星娜, 张青松, 戚瀚鹏, 等. 基于计算流体动力学的锂离子电池热失控多米诺效应研究[J].科学技术与工程, 2014, 14(33): 327–332. LUO X N, ZHANG Q S, QI H P, et al. Lithium-ion battery thermal runaway domino effect analysis based on the CFD[J].Science Technology and Engineering, 2014, 14(33): 327–332.DOI:10.3969/j.issn.1671-1815.2014.33.062(in Chinese)
[5]	张青松, 姜乃文, 罗星娜, 等. 锂离子电池热失控多米诺效应实证研究[J].科学技术与工程, 2016, 16(10): 252–256. ZHANG Q S, JIANG N W, LUO X N, et al. Lithium-ion battery thermal runaway domino effect experimental verification research[J].Science Technology and Engineering, 2016, 16(10): 252–256.DOI:10.3969/j.issn.1671-1815.2016.10.050(in Chinese)
[6]	Standards Policy and Strategy Committee.Reaction-to-fire tests-Heat release, smoke production and mass loss rate:BS ISO 5660-1[S]. London:British Standard Institution, 2015:16-17.
[7]	FU Y, LU S, LI K, et al. An experimental study on burning behaviors of 18650 lithium ion batteries using a cone calorimeter[J].Journal of Power Sources, 2015, 273: 216–222.DOI:10.1016/j.jpowsour.2014.09.039
[8]	HUANG P, WANG Q, LI K, et al. The combustion behavior of large scale lithium titanate battery[J].Scientific Reports, 2015, 5: 77–88.
[9]	PING P, WANG Q, HUANG P, et al. Thermal behaviour analysis of lithium-ion battery at elevated temperature using deconvolution method[J].Applied Energy, 2014, 129: 261–273.DOI:10.1016/j.apenergy.2014.04.092
[10]	FINEGAN D P, SCHEEL M, ROBINSON J B, et al.In-operando high-speed tomography of lithium-ion batteries during thermal runaway[J/OL]. Nature Communications, 2015, 6:2-4[2016-03-15].http://www.nature.com/ncomms/2015/150428/ncomms7924/full/ncomms7924.html.
[11]	FENG X, FANG M, HE X, et al. Thermal runaway features of large format prismatic lithium ion battery using extended volume accelerating rate calorimetry[J].Journal of Power Sources, 2014, 255: 294–301.DOI:10.1016/j.jpowsour.2014.01.005
[12]	JHU C Y, WANG Y W, WEN C Y, et al. Self-reactive rating of thermal runaway hazards on 18650 lithium-ion batteries[J].Journal of Thermal Analysis and Calorimetry, 2011, 106(1): 159–163.DOI:10.1007/s10973-011-1452-6
[13]	戚瀚鹏, 张青松, 宋广韬. 非稳态火源热释放速率等效合成模型研究[J].安全与环境学报, 2015, 15(4): 131–134. QI H P, ZHANG Q S, SONG G T. Innovated synthesis model of the heat releasing rate for the non-steady state fires[J].Journal of Safety and Environment, 2015, 15(4): 131–134.(in Chinese)
[14]	LIU X, STOLIAROV S I, DENLINGER M, et al. Comprehensive calorimetry of the thermally-induced failure of a lithium ion battery[J].Journal of Power Sources, 2015, 280: 516–525.DOI:10.1016/j.jpowsour.2015.01.125
[15]	张雯霞. 锂离子电池电解液的锥形量热仪研究[D]. 合肥: 中国科学技术大学, 2015. ZHANG W X.Experimental study of electrolytes of lithium ion batteries by cone calorimeter[D]. Hefei:University of Science and Technology of China, 2015(in Chinese).
[16]	胡棋威. 锂离子电池热失控传播特性及阻断技术研究[D]. 北京: 中国舰船研究院, 2015. HU Q W.Study on lithium-ion batteries thermal runaway propagation characteristics and blocking techniques[D]. Beijing:China Ship Research and Development Academy, 2015(in Chinese).
[17]	WU P, ROMBERG J, FENG X, et al.Thermal runaway propagation within module consists of large format li-ion cells[C]//Proceedings of SAE-China Congress 2015:Selected Papers.Beijing:Springer, 2015:127-133.
[18]	LAMB J, ORENDORFF C J, STEELE L A M, et al. Failure propagation in multi-cell lithium ion batteries[J].Journal of Power Sources, 2015, 283: 517–5230.DOI:10.1016/j.jpowsour.2014.10.081
[19]	HATCHARD T D, MACNEIL D D, STEVENS D A, et al. Importance of heat transfer by radiation in Li-ion batteries during thermal abuse[J].Electrochemical and Solid-State Letters, 2000, 3(7): 305–308.
[20]	WANG Q, PING P, ZHAO X, et al. Thermal runaway caused fire and explosion of lithium ion battery[J].Journal of Power Sources, 2012, 208: 210–224.DOI:10.1016/j.jpowsour.2012.02.038