然而,可控热核聚变技术现在还处于一个相当不成熟的阶段。核聚变反应的发生非常困难(因为原子核之间存在很强的库仑排斥作用),必须使反应气体电离成为等离子体并加热至极端的高温。当前一般使用磁约束热核聚变的方法,托卡马克装置是迄今为止最有使用发展前途的磁约束热核聚变装置。2006年11月,欧盟、美国、中国、俄罗斯、日本、韩国和印度七方在巴黎正式签署协议,启动国际热核聚变实验反应堆计划,为将来进一步发展聚变反应堆奠定基础。
聚变能源应用的最终实现除了要解决可控热核聚变这一物理问题之外,在很大程度上决定于可控热核聚变装置托卡马克以及未来反应堆中关键材料问题的解决。核能界公认聚变反应堆材料是开发核聚变能的最关键技术之一。核聚变反应装置面对等离子体材料(plasma facing material)和起机械支撑的结构材料(structural material)的选择尤为关键。面对等离子体材料为托卡马克装置中直接面对等离子体的材料[1-4],而结构材料在面对等离子体材料后面起机械支撑作用[5],它们不断受到来自等离子体的各种粒子如氘、氚、α粒子(氦)和高能中子等的轰击、瞬态高能量沉积或热冲击以及电磁辐射和电磁力的作用。这些作用将造成材料的辐照效应和损伤,导致材料中缺陷的产生、迁移和聚集,引起材料的肿胀和变形。因此面对等离子体材料和结构材料与氚、氦以及杂质氧等的相互作用是制约可控核聚变能最终实现商业应用的关键工程技术问题之一。
钒(V)以及V基合金是现阶段重点发展的核聚变反应堆结构候选材料。V在高温条件下具有良好的力学性能[6-8],在中子辐照的条件下产生的放射性可能性小,活化性能低[9-11];另外它的导热系数高和热膨胀系数小,在服役过程中不容易产生热应力场[12-15]。在磁约束核聚变装置中,锂(Li)作为氚增殖材料得到了广泛青睐,而V与Li之间良好的相容性,也是V成为核聚变反应堆结构候选材料的重要原因[16-18]。但是V基材料在磁约束核聚变反应堆中的应用也存在一些问题,例如在富氢(H)的环境里,V基材料容易吸H而导致氢脆现象;作为聚变反应产物的氦(He)粒子会在V基材料中产生聚集,这将引起材料的起泡和脆化;氧(O)、碳(C)以及氮(N)等杂质溶解在间隙位会对V基材料的拉伸性能、蠕变性能以及断裂性能产生很大的影响。实验研究表明,可以通过添加合金化元素来提高V基材料的性能。例如,添加铬(Cr)元素可强化合金,使合金具有较好的抗高温蠕变和抗腐蚀性能[19];添加钛(Ti)元素可显著增强合金的抗中子辐照的能力[20]。
到目前为止,国内外对杂质如H和He等在V基结构材料中的行为已经进行了大量的实验和理论研究[21-25]。此外,前面已经提到O在金属材料中也是一种比较典型的杂质元素,它会在材料的生产、制造和使用过程中出现,即使浓度很低,它也可以直接影响材料的力学性能。而对于当前聚变托卡马克装置中,一方面作为结构材料V受到高能中子的轰击将产生大量缺陷如空位,而空位极易捕获O杂质形成O-空位团簇(O-vacancy clusters),显著地改变V的微结构,最终导致其力学性能的降低;另一方面,O溶解在间隙位极易扩散会产生诸如脆化、应变老化以及腐蚀等。更为重要的是,近来的实验研究结果直接表明V基材料在高温条件下易于氧化,O含量的升高会使V基材料的延展率显著降低,产生脆化现象[26],这些问题亟待解决。经过大量调研, 笔者发现杂质O在V中的基本行为到目前为止研究工作较少。鉴于此,本文系统研究了杂质O在V中的热力学稳定性、电子结构、扩散行为以及与缺陷空位的相互作用。尽管V与面对等离子体候选材料钨(W)和钼(Mo)的结构相同(它们都是体心立方结构),然而本文发现杂质O在V中的行为与在金属W和Mo中不同,O在V中易于占据八面体间隙位,而在W和Mo[27-28]中易于占据四面体间隙位。在后面的结果与讨论中,本文将从物理的角度给出详细的分析。
1 计算模型及方法 本文采用基于密度泛函理论(density functional theory)的第一性原理方法,使用的计算软件是VASP(Vienna Ab-initio Simulation Package)[29-30]。电子之间的交换关联作用采用广义梯度近似(generalized gradient approximation)的PBE(Perdew-Burke-Ernzerhof) [31]交换关联函数方法来描述(即GGA-PBE形式),离子与电子之间的相互作用通过投影缀加平面波赝势[32]给出。本文首先测试了V的晶格常数,计算时截止能取为较大的600eV。图 1给出了能量随着晶格常数变化的曲线,系统的总能量是系统稳定程度的标志,能量越小晶体的结构越稳定,从图 1可以得到V的平衡晶格常数为0.298nm,与实验值0.303nm[33]相对误差约为1.68%, 然而在误差范围内可以认为与实验值吻合较好。确定完晶格常数之后,本文分别对平面波动能的截止能和k点进行了测试。O在128原子V超晶胞中八面体间隙位(OIS)和四面体间隙位(TIS)中溶解能(EOs(OIS)和EOs(TIS))的测试结果, 如表 1所示,测试结果表明截止能为350eV,而k点选取3×3×3均匀网格的Monkhorst-Pack类型进行布里渊区积分[34]。考虑到周期性边界条件,计算过程中经过测试本文使用了4×4×4单胞结构含有128个原子的超晶胞, 其三边分别沿着[100]、[010]和[001]3个方向截取,且长度都为1.192nm。在所有计算过程中,超晶胞的大小、形状和原子位置都允许自由弛豫,计算结果让所有原子上的作用力均小于10-2 eV/nm。
 |
| 图 1 V的晶格常数与能量的关系曲线 Fig. 1 Energy-lattice constant curve for V |
| 图选项 |
表 1 O在128原子V超晶胞中八面体间隙位和四面体间隙位中溶解能的测试结果 Table 1 Tested solution energy results of O at OIS and TIS in 128-atom V supercell
| eV | |||||||||
| 测试对象 | 截止能 | k点 | |||||||
| 250 | 300 | 350 | 400 | 450 | 1×1×1 | 2×2×2 | 3×3×3 | 4×4×4 | |
| EOs(OIS) | -4.928 | -4.935 | -4.942 | -4.943 | -4.943 | -4.902 | -4.935 | -4.942 | -4.942 |
| EOs(TIS) | -3.693 | -3.761 | -3.779 | -3.778 | -3.778 | -3.689 | -3.762 | -3.779 | -3.778 |
| 注:先选取一个较大的8×8×8 k点对截止能进行测试,测试结果取为350 eV,并采用350 eV的截止能对k点进行测试,测试结果取为3×3×3 k点。 | |||||||||
表选项
对于O在本征V中的热力学稳定性,本文考虑了2个典型的间隙位(四面体间隙位和八面体间隙位)和替代位。当O占据间隙位(interstitial site)时,溶解能定义为
 | (1) |
式中:EV, i-O为V超晶胞体系含有一个间隙O原子时的总能量;EV为纯V超晶胞体系的总能量;μO为O的化学势。关于氧的化学势μO,它是一个自由O2分子能量的一半,根据当前第一性原理计算,μO为-4.416eV。当O占据替代位(substitution site)时,溶解能定义为
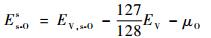 | (2) |
式中:EV, s-O为V超晶胞体系含有一个替位O原子时的总能量。
对于O与空位(vacancy)的相互作用,本文考虑了O原子被空位捕获时的情况,其捕获能(trapping energy)定义为
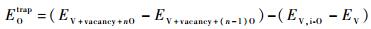 | (3) |
式中:EV+vacancy+nO和EV+vacancy+(n-1) O分别为V超晶胞体系中空位含有n个O原子和n-1个O原子的总能量。
对于O原子在本征V中的扩散行为,扩散系数本文利用Arrhenius[35]扩散方程:
 | (4) |
式中:D0为不依赖于温度的扩散前因子;Ea为扩散激活能,为O原子在过渡态(transition state)位置和初始态(initial state)位置能量(Ets和Eis)之间的差值,即Ea=Ets-Eis;k为玻尔兹曼常数;T为温度。根据Zener和Wert理论[36],
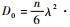
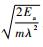
2 计算结果与分析讨论 2.1 O在V中的热力学性能
2.1.1 O的溶解能 首先计算O在间隙位时的溶解能,由于V为体心立方(body center cubic)结构,因此本文只考虑2种高对称情况,即O原子占据四面体间隙位和八面体间隙位。计算结果表明,单个O原子易于占据八面体间隙位,其溶解能为-4.942eV;而当O原子占据四面体间隙位时,溶解能为-3.779eV,比占据八面体的溶解能高1.163eV。有趣的是,如果将O原子稍微偏离四面体间隙位,本文发现晶胞结构优化之后O原子会自动弛豫到八面体间隙位,这说明四面体间隙位只是O原子存在的过渡态。关于O原子扩散过程中的过渡态, 本文将在扩散部分给出详细讨论。
接下来本文讨论O原子占据替代位时的情况。根据式(2) 本文计算得到了O原子替代位的溶解能,其值为-3.214eV,可以看到这个值比O原子占据八面体间隙位和四面体间隙位的溶解能分别高出1.728eV和0.565eV,这意味着从能量的角度说明O原子不易于占据替位中心。
2.1.2 原子结构和电荷分布 进一步分析原子结构和电荷密度分布。图 2给出了O分别占据替代位、四面体间隙位和八面体间隙位时的原子结构和相对应的价电荷密度分布,图中红球和灰球分别代表V原子和O原子。O原子与近邻的V原子价电荷密度分布在一定程度上可以揭示了原子成键的特征。由图 2(a)可以看到,当O占据替代位时,O和最近邻的V原子之间的电荷密度非常低,表明它们之间存在非常弱的相互作用,没有明显的键和特性。这可以解释O占据替代位时为什么具有较高的溶解能。此外,O占据替代位位置时除了与V键合较弱之外,O替位掉本征V中的一个V原子也是其占据此位置溶解能高的原因。如图 2(b)所示,四面体间隙O周围存在4个最近邻的V原子,可以看到O与4个最近邻的V原子存在相同的相互作用,类共价(covalent-like)特征的键明显形成。与杂质H或He相比,由于O原子的半径(0.074nm)比较大,当O原子处于四面体间隙位时,它引起的晶胞膨胀现象比较明显。从图 2(b)中可以看出,O原子的加入导致最近邻的4个V原子明显的向外移动。对于O占据八面体间隙位时,O周围分别存在2个最近邻和4个次近邻V原子(如图 2(c)所示)。由电荷密度分布可以看出,O占据八面体间隙与4个次近邻的V原子存在明显的键和特性,键的强弱与O占据四面体间隙位时的情况相当;然而与2个最近邻的V原子存在非常强的相互作用,类共价特征的键明显形成(如图 2(c)所示)。可以看出,与四面体间隙O相比,八面体间隙O相当于多出2个近邻的V原子,即多出了2个共价键,这使得O原子占据八面体间隙位时溶解能进一步降低。因此,从电荷密度分布的特征在一定程度上可以解释O在V中最容易占据八面体间隙位。
 |
| 图 2 O在V中的原子结构和价电荷密度分布 Fig. 2 Atomic structure and valence charge density distribution of O in V |
| 图选项 |
2.1.3 态密度 为了进一步得出O易于占据八面体间隙位时的物理原因,本文计算了O占据V中八面体间隙位时体系总的态密度,并与纯V体系总的态密度进行对比,如图 3(a)所示。图 3中:费米能设为能量零点。可以看出,与纯V体系相比含O的V体系中总的态密度在费米能附近的最高峰值轻微有所下降,形状基本没有什么变化;然而在低能区域却出现了一个明显的小峰,可以肯定的说小峰的出现与O原子的加入直接相关。
 |
| 图 3 态密度 Fig. 3 Density of states |
| 图选项 |
弄清楚O加入后V体系中小峰的来源,本文进一步分析了纯V体系和O占据八面体间隙位时V体系第一近邻(1NN)V原子d轨道电子局域态密度的变化,如图 3(b)所示。可以看到,含O的V体系第一近邻V原子的d轨道比纯V体系d轨道的峰值有所降低,并在低能部分出现了一个次高峰。图 3(c)给出了纯O和V中八面体间隙位上O的p轨道电子态密度。对于纯O,p轨道电子在低能区域形成很强的峰(图 3(c)中的红线),但当O在V中占据八面体间隙位后,峰不但进一步向低能区域移动,而且峰值与纯O相比有所升高(图 3(c)中的黑线)。这说明由于O的存在,V原子的d轨道电子发生了转移,并与O的p轨道电子发生了杂化。这种O-p和V-d杂化现象有利于原子之间共价键的形成。
2.2 O在V中的扩散特性 扩散特性对于理解O在金属V中的行为非常重要,一方面,在材料当中作为一个最基本的参数,扩散系数会影响O在V中的滞留和迁移;另一方面,扩散系数也是决定扩散速度的重要指数,它可以定量地反映O的扩散行为。因此,本文研究了O在本征V中的扩散特性。
前面的热力学计算结果表明,O原子在V中占据八面体间隙位最稳定,因此根据攀爬轻推弹性带方法[37]本文首先设置2个最近邻的八面体间隙位为初、末位置,然后在它们之间插入19个点,即本文相当于选取了21个点同时进行弛豫计算。结果表明O在四面体间隙位时为其过渡态鞍点,扩散激活能Ea为O在四面体间隙位和八面体间隙位时溶解能量的差值。因此,O在体心立方金属V当中的最佳扩散路径是从初始的八面体间隙位经过中间四面体间隙位向另一个最近邻的八面体间隙位迁移,即八面体间隙位→四面体间隙位→八面体间隙位(Octahedral→Tetrahedral→Octahedral, O→T→O)。图 4给出了相应的扩散激活能,其值为1.728eV。
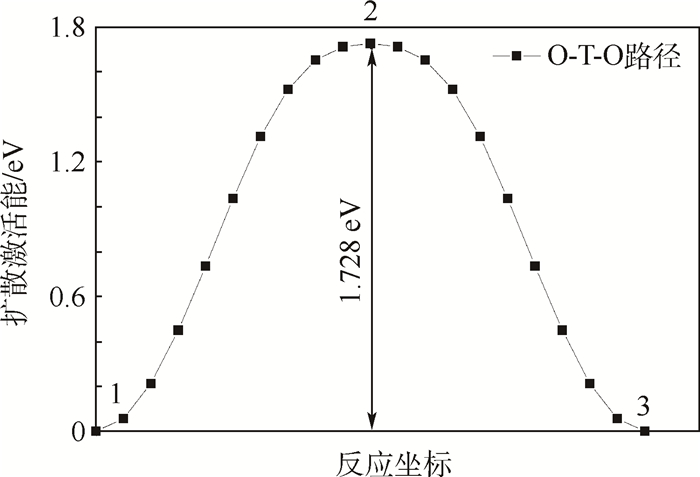 |
| 图 4 O在V中间隙位的扩散能垒 Fig. 4 Diffusion energy barrier of O at interstitial sites in V |
| 图选项 |
O占据初始的八面体间隙位向周围最近邻的八面体间隙位跳跃时,由于金属V为体心立方结构,周围存在4个最近邻的相同的面体间隙位,因此跳跃位置的数量n为4,跳跃长度λ为a/2(a为V的晶格常数0.298nm)。把O原子在V中间隙位时的扩散激活能Ea=1.728eV以及n、λ和O原子的质量代入式(4),可以得出D0为2.30×10-7 m2/s。进一步结合Arrhenius扩散方程(4),O在本征V中间隙位的扩散系数为D=2.30×10-7exp(-1.728 eV/kT) m2/s。为了更清楚地了解O在V中的扩散速率,本文给出了温度范围在300~1000K之间的扩散系数,如表 2所示。
表 2 O在V中300 ~1000K温度范围内的扩散系数 Table 2 Diffusion coefficient of O in V at different temperatures from 300 to 1000K
| T/K | D/(m2·s-1) |
| 300 | 2.16×10-36 |
| 400 | 3.91×10-29 |
| 500 | 8.84×10-25 |
| 600 | 7.05×10-22 |
| 700 | 8.35×10-20 |
| 800 | 3.00×10-18 |
| 900 | 4.86×10-17 |
| 1000 | 4.51×10-16 |
表选项
由表 2可以看到,当温度分别为600和1000K时,扩散系数分别为7.05×10-22和4.51×10-16m2/s。
2.3 O在V中与缺陷空位的相互作用 作为金属以及其他材料中比较典型的缺陷,空位在缺陷成核、演化以及扩散过程中充当着非常重要的作用,而且对于在不同金属[38-41]中观察到的宏观变形和失效最终起决定性作用。同时,在聚变托卡马克装置中高能中子对V的轰击也会导致空位产生。因此本文进一步研究了O在V中与空位的相互作用。
2.3.1 单个O原子与空位的相互作用 本文把单个O原子放在空位附近几个可能稳定位置,如空位中心、空位附近的四面体和八面体间隙位等。结构优化结果如图 5所示,图中的蓝球和红球分别代表O原子和V原子。单个O原子倾向于结合在空位内表面的一个类球状的等值面电子密度约为1.2×1029个/m3的区域(如图 5(a)所示)。尽管类球状的区域都是O可能的稳定位置,然而O最稳定的位置为接近于八面体间隙位离空位中心约0.139nm(见图 5(b)),并且存在6个等价的能量最低位置,如图 5(a)标“+”的6个点。根据式(3) 捕获能的计算,本文进一步发现O在空位中6个等价的最稳定位置存在较大的捕获能,其值为-0.484eV,可以看到这个能量远远低于O在本征V中稳定的八面体间隙位时的能量。此外,O在类球状区域中其它位置的捕获能高出6个等价最稳定位置约为0.200eV,这也是反映了额外原子结构对O与近邻V原子相互作用的影响。
 |
| “+”代表O结合在等值面的6个能量最低位置。 图 5 O与空位结合的最佳电子密度等值面 Fig. 5 Isosurface of optimal electron density for O binding at one vacancy |
| 图选项 |
O在空位中存在较大的捕获能主要来源于O占据6个等价能量最低的等值面电子密度约为120个/nm3位置有利于O和近邻的V原子形成共价键。图 6给出了“O1-vacancy”团簇(O1-vacancy cluster)在(001) 平面上的原子结构和电荷密度分布,图中的蓝球和红球分别代表O原子和V原子。可以看到此时O与近邻的V原子能形成方向性很强的O-V共价键。这种O在空位与近邻V原子成键的物理机制将会使得O原子偏离空位中心形成反对称的“O-空位(O-vacancy)对结构”,这在一定程度上可以解释O为什么不占据空位中心(2.1.1节)。到目前为止,很少发现实验上对V的研究中提到关于反对称的“O-空位对”结构的报道,然而早期的正电子湮灭(positron-lifetime)实验研究中[42],在体心立方结构铁(α-Fe)中已经发现了反对称的“C-空位(C-vacancy)对结构”,这来源于C原子易于结合在空位内表面6个等价的最稳定位置与近邻Fe原子形成共价键。类似于在α-Fe的情况,本文认为在V中O原子同样倾向于结合在空位内表面6个等价的最稳定位置与近邻V原子形成共价键而不是呆在空位中心,因此O原子不得不偏离空位中心形成反对称的“O-空位对结构”。
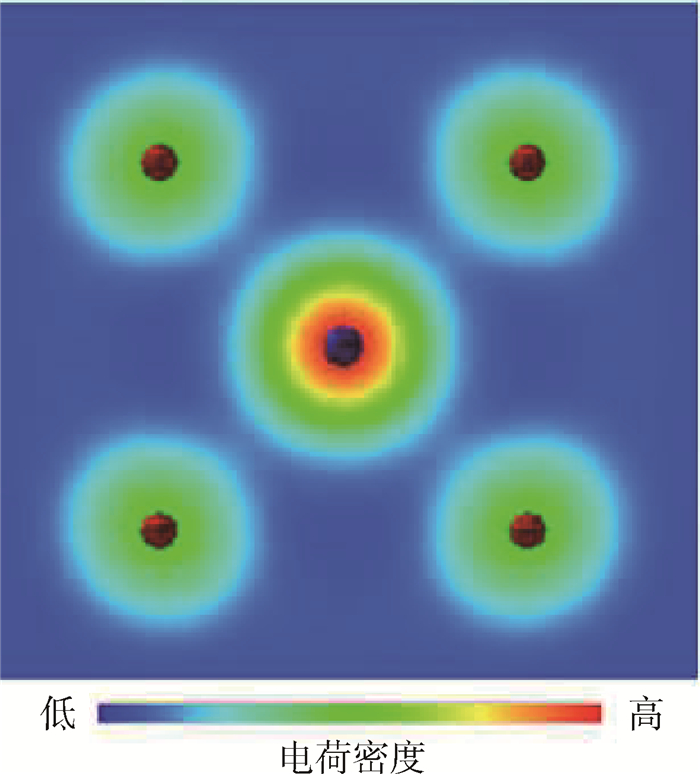 |
| V原子和O原子分别处在不同的(001) 平面。 图 6 “O1-vacancy”团簇在(001) 平面上的电荷密度分布 Fig. 6 Charge density distribution of "O1-vacancy" cluster on (001) plane |
| 图选项 |
逐渐地把O原子放入空位并在每一步优化结构使得O原子找到稳定的位置。理论上,空位存在6个等价的能量最低的等值面电子密度位置,第1个O原子进入之后将任意的占据其中之一,如图 5(a)和5(b)所示。图 7给出了随着O原子数目的增加O在空位中的捕获能,O占据离空位很远处八面体间隙位时的能量作为参考点。可以看到位于等值面上的第1个O原子的捕获能为-0.484eV,根据Oint+On-1-vacancy→On-vacancy团簇形成过程,此时“O1-vacancy”团簇的形成来自于Oint+vacancy→O1-vacancy,同时会导致0.484eV的能量释放。随着O原子数目的增加,O—O之间将经历一定的相互作用。当第2个O原子进入之后,Oint+O1-vacancy→O2-vacancy导致“O2-vacancy”团簇形成,其捕获能进一步降低,为-0.510eV。因此,“O2-vacancy”团簇的形成将导致0.510eV能量释放,而且O占据位置的最佳电子密度面也在相应的逐渐收缩(见图 5(c))。本文进一步发现“O2-vacancy”团簇最稳定的构型为2个O原子沿着 < 001>方向排列,且分别位于2个等价的接近于八面体间隙位的位置,这2个位置距离空位中心约为0.137nm。随着O原子数目的进一步增加,Oint+O2-vacancy→O3-vacancy导致“O3-vacancy”团簇形成,然而此时捕获能变为正值0.382eV,这个能量值明显高于O占据远离空位的本征八面体间隙位(图 7中的参考点)时的能量,因此“O3-vacancy”团簇不能形成,单空位最多可以容纳2个O原子。也就是说,在V中只存在形成“O1-vacancy”团簇和“O2-vacancy”团簇的可能。
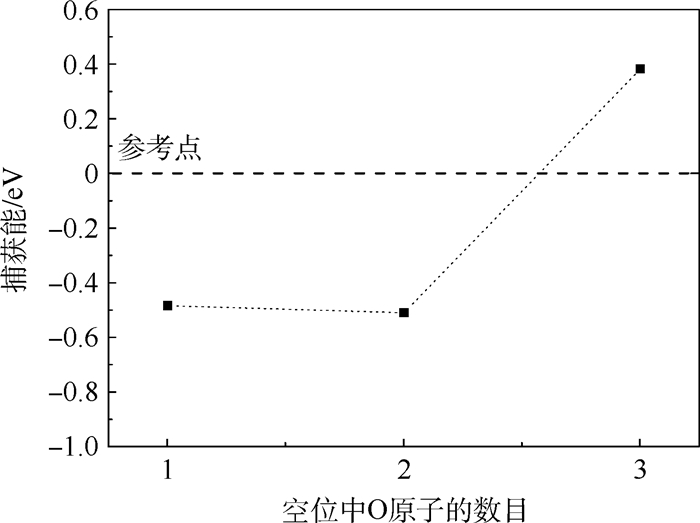 |
| 图 7 O在V中以“sequential”方式进入单空位时捕获能随O原子数目增加的变化曲线 Fig. 7 Changing curve of trapping energy of O with increase of number of atoms at one vacancy in V via "sequential" way |
| 图选项 |
2.3.2 多个O原子与空位的相互作用 单个O原子的结果表明,O和空位在V中存在较强的结合。这意味着空位可能作为一个捕获中心使得间隙位中的O原子向空位偏析。为了调查这种可能性,本文计算了额外O原子在空位中的捕获能以至于确定单空位捕获O原子的数量。
3 结论 1) 杂质O在V中易于占据八面体间隙位,其溶解能为-4.942eV。
2) 利用攀爬轻推弹性带方法方法,本文发现O在间隙位的最佳扩散路径为八面体间隙位→四面体间隙位→八面体间隙位,扩散激活能为1.728eV,并在此基础上本文给出了不同温度条件下O在V中的扩散系数。
3) O在V中与空位存在很强的吸引相互作用,1个O和2个O被空位捕获时的捕获能分别为-0.484eV和-0.510eV,3个O的捕获能为0.382eV,这表明V中O-空位团簇很容易形成,但单空位最多只能结合2个O原子。这些结果将为核聚变结构材料的选择和制备提供必要的参考依据。
参考文献
| [1] | LIU Y L, ZHOU H B, JIN S, et al. Effects of H on electronic structure and ideal tensile strength of W:A first-principles calculation[J].Chinese Physics Letters, 2010, 27(12): 127101.DOI:10.1088/0256-307X/27/12/127101 |
| [2] | LIU Y L, JIN S, ZHANG Y, et a. l Interaction between impurity nitrogen and tungsten:A first-principles investigation[J].Chinese Physics B, 2012, 21(1): 016105.DOI:10.1088/1674-1056/21/1/016105 |
| [3] | LIU Y L, GAO A Y, LU W, et al. Optimal electron density mechanism for hydrogen on the surface and at a vacancy in tungsten[J].Chinese Physics Letters, 2012, 29(7): 077101.DOI:10.1088/0256-307X/29/7/077101 |
| [4] | LIU Y L, LU W, GAO A Y, et al. First-principles investigation on diffusion behaviours of H isotopes:From W(110) surface into bulk and in bulk W[J].Chinese Physics B, 2012, 21(12): 126103.DOI:10.1088/1674-1056/21/12/126103 |
| [5] | LIU Y L, ZHANG Y, HONG R J, et al. Study of theoretical tensile strength of Fe by a first-principles computational tensile test[J].Chinese Physics B, 2009, 18(5): 1923–1930.DOI:10.1088/1674-1056/18/5/033 |
| [6] | SMITH D L, CHUNG H M, LOOMIS B A, et al. Reference vanadium alloy V-4Cr-4Ti for fusion application[J].Journal of Nuclear Materials, 1996, 233-237: 356–363.DOI:10.1016/S0022-3115(96)00231-0 |
| [7] | CHUNG H M, LOOMIS B A, SMITH D L. Development and testing of vanadium alloys for fusion applications[J].Journal of Nuclear Materials, 1996, 239: 139–156.DOI:10.1016/S0022-3115(96)00676-9 |
| [8] | SATOU M, ABE K, KAYANO H. High-temperature deformation of modified V-Ti-Cr-Si type alloys[J].Journal of Nuclear Materials, 1991, 179: 757–761. |
| [9] | SATO S, TANAKA T, HORI J, et al. Radioactivity of the vanadium-alloy induced by D-T neutron irradiation[J].Journal of Nuclear Materials, 2004, 329: 1648–1652. |
| [10] | MARKOVSKIJ D V, FORREST R A, KOVALCHUK V D, et al. Experimental activation study of some Russian vanadium alloys with 14-MeV neutrons at SNEG-13 facility[J].Fusion Engineering and Design, 2001, 58: 591–594. |
| [11] | BLOOM E E, CONN R W, DAVIS J W, et al. Low activation materials for fusion applications[J].Journal of Nuclear Materials, 1984, 122(1): 17–26. |
| [12] | BUTTERWORTH G J, MCCARTHY K A, SMOLIK G R, et al. Safety and environmental aspects of vanadium alloys[J].Journal of Nuclear Materials, 1994, 212: 667–672. |
| [13] | TSAI H, BRAY T S, MATSUI H, et al. Effects of low-temperature neutron irradiation on mechanical properties of vanadium-base alloys[J].Journal of Nuclear Materials, 2000, 283: 362–366. |
| [14] | LOOMIS B A, SMITH D L, GARNER F A. Swelling of neutron-irradiated vanadium alloys[J].Journal of Nuclear Materials, 1991, 179: 771–774. |
| [15] | OHNUKI S, TAKAHASHI H, KINOSHITA H, et al. Void formation and precipitation in neutron irradiated vanadium alloys[J].Journal of Nuclear Materials, 1988, 155: 935–939. |
| [16] | LOOMIS B A, SMITH D L. Vanadium alloys for structural applications in fusion systems:A review of vanadium alloy mechanical and physical properties[J].Journal of Nuclear Materials, 1992, 191: 84–91. |
| [17] | BORGSTEDT H U, GRUNDMANN M, KONYS J, et al. A vanadium alloy for the application in a liquid metal blanket of a fusion reactor[J].Journal of Nuclear Materials, 1988, 155: 690–693. |
| [18] | BORGSTEDT H U, FEUERSTEIN H. The solubility of metals in Pb-17Li liquid alloy[J].Journal of Nuclear Materials, 1992, 191: 988–991. |
| [19] | SMITH D L, CHUNG H M, LOOMIS B A, et al. Development of vanadium-base alloys for fusion first-wall—Blanket applications[J].Fusion Engineering and Design, 1995, 29: 399–410.DOI:10.1016/0920-3796(95)80046-Z |
| [20] | LOOMIS B A, HULL A B, SMITH D L. Evaluation of low-activation vanadium alloys for use as structural material in fusion reactors[J].Journal of Nuclear Materials, 1991, 179: 148–154. |
| [21] | SATO T, OKITA T, SEKIMURA N. Effects of solid transmutation and helium on microstructural evolution in neutron-irradiated vanadium[J].Journal of Nuclear Materials, 2002, 307: 385–388. |
| [22] | 谌继明, 室贺健夫, 许增裕, 等. 聚变应用钒合金抗氢脆性能的合金化设计[J].金属学报, 2002, 38(8): 839–843. CHEN J M, MUROGA T, XU Z Y, et al. Alloying design for fusion application vanadium alloys based on hydrogen embrittlement resistance[J].Acta Metallurgica Sinica, 2002, 38(8): 839–843.(in Chinese) |
| [23] | 吴仲成, 彭述明, 杨茂年, 等. 有效介质理论计算He原子在金属钒中的扩散行为[J].金属学报, 2004, 40(1): 36–39. WU Z C, PENG S M, YANG M N, et al. Calculation of diffusion barriers for helium atom in vanadium by effective medium theory[J].Acta Metallurgica Sinica, 2004, 40(1): 36–39.(in Chinese) |
| [24] | ZHANG P B, ZHAO J J, QIN Y, et al. Stability and dissolution of helium-vacancy complexes in vanadium solid[J].Journal of Nuclear Materials, 2011, 419: 1–8.DOI:10.1016/j.jnucmat.2011.08.023 |
| [25] | ZHANG P B, ZHAO J J, QIN Y, et al. Stability and migration property of helium and self defects in vanadium and V-4Cr-4Ti alloy by first-principles[J].Journal of Nuclear Materials, 2011, 413: 90–94.DOI:10.1016/j.jnucmat.2011.03.031 |
| [26] | KURTZ R J, ABE K, CHERNOV V M, et al. Recent progress on development of vanadium alloys for fusion[J].Journal of Nuclear Materials, 2004, 329: 47–55. |
| [27] | ALKHAMEES A, ZHOU H B, LIU Y L, et al. First-principles investigation on dissolution and diffusion of oxygen in tungsten[J].Journal of Nuclear Materials, 2009, 393: 508–512.DOI:10.1016/j.jnucmat.2009.07.012 |
| [28] | ALKHAMEES A, ZHOU H B, LIU Y L, et al. Vacancy trapping behaviors of oxygen in tungsten:A first-principles study[J].Journal of Nuclear Materials, 2013, 437: 6–10.DOI:10.1016/j.jnucmat.2013.01.317 |
| [29] | KRESSE G, HAFNER J. Ab initio molecular dynamics for liquid metals[J].Physical Review B, 1993, 47(1): 558–561.DOI:10.1103/PhysRevB.47.558 |
| [30] | KRESSE G, FURTHMVLLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J].Physical Review B, 1996, 54(16): 11169–11186.DOI:10.1103/PhysRevB.54.11169 |
| [31] | PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple[J].Physical Review Letters, 1996, 77: 3865–3868.DOI:10.1103/PhysRevLett.77.3865 |
| [32] | KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method[J].Physical Review B, 1999, 59(3): 1758–1775.DOI:10.1103/PhysRevB.59.1758 |
| [33] | KITTEL C. Introduction to solid state physics[M].7th edNew York: Wiley, 1996. |
| [34] | MONKHORST H J, PACK J D. Special points for Brillouin-zone integrations[J].Physical Review B, 1976, 13(12): 5188–5192.DOI:10.1103/PhysRevB.13.5188 |
| [35] | HOGLUND L, AGREN J. Simulation of carbon diffusion in steel driven by a temperature gradient[J].Journal of Phase Equilibria and Diffusion, 2010, 31(3): 212–215.DOI:10.1007/s11669-010-9673-0 |
| [36] | WERT C, ZENER C. Interstitial atomic diffusion coefficients[J].Physical Review, 1949, 76(8): 1169–1175.DOI:10.1103/PhysRev.76.1169 |
| [37] | HENKELMAN G. A climbing image nudged elastic band method for finding saddle points and minimum energy paths[J].Journal of Chemical Physics, 2000, 113(22): 9901–9904.DOI:10.1063/1.1329672 |
| [38] | FUKAI Y, ōKUMA N. Formation of superabundant vacancies in Pd hydride under high hydrogen pressures[J].Physical Review Letters, 1994, 73(12): 1640–1643.DOI:10.1103/PhysRevLett.73.1640 |
| [39] | LU G, KAXIRAS E. Hydrogen embrittlement of aluminum:The crucial role of vacancies[J].Physical Review Letters, 2005, 94(15): 155501.DOI:10.1103/PhysRevLett.94.155501 |
| [40] | GAVINI V, BHATTACHARYA K, ORTIZ M. Vacancy clustering and prismatic dislocation loop formation in aluminum[J].Physical Review B, 2007, 76(18): 180101.DOI:10.1103/PhysRevB.76.180101 |
| [41] | DISTEFANO J R, DEVAN J H. Reactions of oxygen with V-Cr-Ti alloys[J].Journal of Nuclear Materials, 1997, 249: 150–158.DOI:10.1016/S0022-3115(97)00217-1 |
| [42] | HAUTOJARVI P, JOHANSSON J, VEHANEN A. Vacancy-carbon interaction in iron[J].Physical Review Letters, 1980, 44(20): 1326–1329.DOI:10.1103/PhysRevLett.44.1326 |
