作为国内最早从事超声悬浮轴承研究的机构,吉林大学先后开展了超声推力悬浮轴承、双向支撑超声悬浮轴承、超声悬浮/气浮混合悬浮轴承等研究工作[2-4]。南京航空航天大学精密驱动研究所成功研制出可用于微小超声电机mN·m量级扭矩测试的超声轴承以及超声悬浮球面轴承[5-6]。国外,南洋理工大学Zhao等[7-8]提出了基于多个周向分布换能器的超声波径向悬浮轴承,并从非线性声学理论和流体动力学理论的角度对轴承悬浮力进行了数值分析。东京理科大学Yoshimoto等[9-10]率先提出了基于弹性铰链的超声悬浮轴承,利用弹性铰链减弱结构刚度的方法使轴承结构在振动时产生挤压膜。其研究工作为超声波悬浮轴承的研究开拓了新思路。布鲁内尔大学Ha[11]等和Stolarski[12]则在Yoshimoto等[9-10]的研究基础上进行了改进和拓展,探索出一种在传统气体动压轴承中产生挤压膜的新方法,研制出自悬浮空气动压轴承,解决了气体动压轴承在启停和低速时摩擦磨损严重的问题。与Yoshimoto等[9-10]的设计理念相反,布鲁内尔大学Wang和Au[13-15]提出了一种借助鳍状凸台加强结构刚度获得挤压膜的方法,研制出一种新型的管状挤压膜径向轴承。
本文提出了一种新型超声悬浮轴承,其利用辐射端沟槽结构将压电换能器产生的单向纵振转换为径向和轴向的双向振动。振动产生的气体挤压膜可实现对轴颈的径向和轴向支承。相比其他超声悬浮轴承结构,该超声轴承仅需一个压电换能器驱动即可实现对径向和轴向载荷的支承,结构更为简单紧凑。为验证新方案可行性,本文对超声轴承工作参数进行了分析与测试,对轴承悬浮承载力进行了预估。
1 超声轴承工作参数的确定 如图 1所示,本文设计的超声悬浮轴承结构主要包括4个组件:轴承座、超声换能器、辐射头和轴颈。根据压电陶瓷材料的逆压电效应,超声换能器在超声频交流电激励下可产生高频机械振动 (换能器振动频率一般在16 kHz以上)。压电陶瓷片产生的纵向振动经变幅杆放大后,向轴承辐射头传递。轴承辐射头中的“┤├”型沟槽结构可将单向纵振转换成辐射头上凹面的纵振和两侧面的弯振。凹面纵振产生的声辐射力为轴承提供径向力;侧面弯振产生的声辐射力为轴承提供轴向力。振动产生的声辐射力的大小决定了超声轴承承受径向和轴向载荷的能力。影响超声轴承工作性能的主要控制性参数是工作频率、声阻抗、辐射端输出振幅和气膜厚度。借助理论、仿真和测试等手段获取上述参数,可为超声轴承的原理验证、悬浮特性研究提供依据。
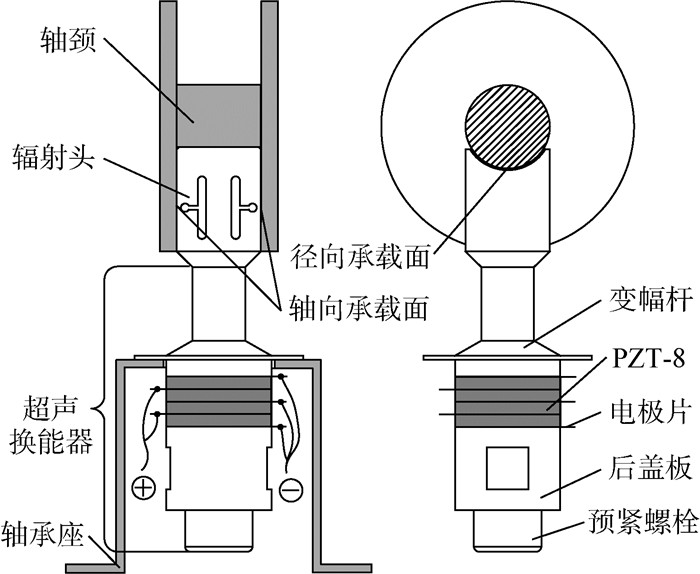 |
| 图 1 超声悬浮轴承结构简图 Fig. 1 Schematic of ultrasonic levitating bearing structure |
| 图选项 |
1.1 超声轴承工作频率和阻抗的预测 超声轴承只有工作在谐振频率下,且换能器和驱动电路的阻抗匹配合理时,才能获得较高的电声转换效率。为准确预测超声轴承的工作频率和阻抗,使轴承承载面输出良好的振动效果,基于力-电-声类比方法,建立超声轴承的声阻抗网络模型。如图 2所示,超声轴承的总声阻抗为预紧螺栓、后盖板、压电陶瓷叠堆、变幅杆和辐射头5部分结构的声阻抗之和。每一部分结构声阻抗均可等效为一个“T型”电学网络。求得每一个“T型”电学网络中的等效阻抗后,将各部分声阻抗串联起来,即可求得超声轴承的总声阻抗网络模型。
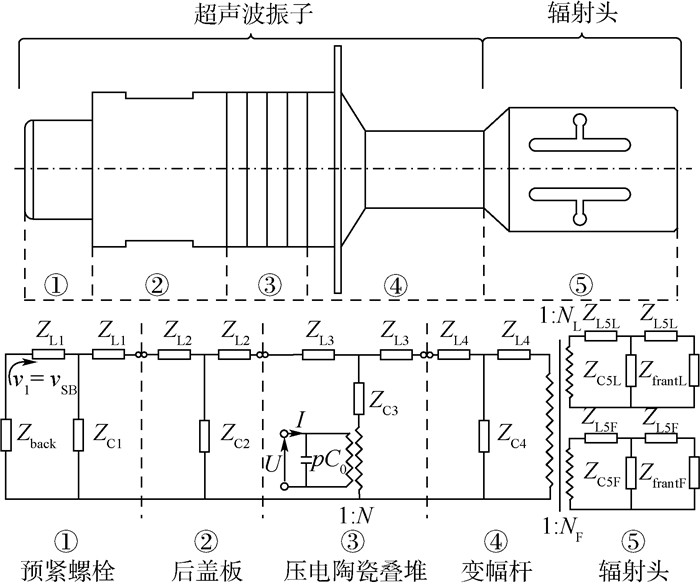 |
| ZL1~ZL4—第1段~第4段水平特征阻抗; ZL5L—第5段水平纵振特征阻抗; ZfrantL—辐射面纵振负载阻抗; ZC1~ZC4—第1段~第4段竖直特征阻抗; ZL5F—第5段水平弯振特征阻抗; ZC5L—第5段竖直纵振特征阻抗; ZC5F—第5段竖直弯振特征阻抗; ZfrantF—辐射面弯振负载阻抗; Zback—后盖板负载阻抗; v1—后盖板后端面振速; vSB—螺栓螺帽振速; U—陶瓷叠堆激励电压; I—流经陶瓷的电流; p—陶瓷片数目; C0—陶瓷片静态截止电容; N—陶瓷输出电压与输入电压之比; NL—输出与输入纵振力之比; NF—输出与输入弯振力之比。 图 2 超声轴承声阻抗网络模型 Fig. 2 Acoustic impedance network model of ultrasonic bearing |
| 图选项 |
模型中超声换能器的声阻抗表达式为
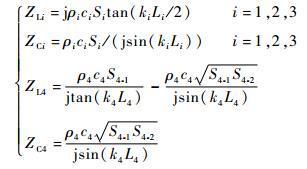 | (1) |
式中:ρi、ci、Si、ki和Li分别为第i段的平均密度、平均波速、横截面积、波数以及特征长度;S4-1和S4-2分别为第4段结构-变幅杆的大端和小端横截面积。计算超声变幅杆的声阻抗时,波阻变化小,且连续过渡,可以忽略圆锥过渡段的影响。
沟槽结构的功能是将变幅杆输出端的纵向振动转换成辐射头凹面的纵振和辐射头侧面的弯振。辐射头的结构参数如图 3所示,根据机电系统类比方法知,振动力 (力矩) 之比为电压之比,得辐射头输出纵振力FL与输入纵振力F之比NL=FL/F=l1/l,l1为辐射头主槽跨距,l为辐射头宽度,输出弯振力矩M与输入纵振力F之比NF=2M/F≈(l2+l3)2/l,l2和l3分别为辐射头主槽宽度和翼槽长度。
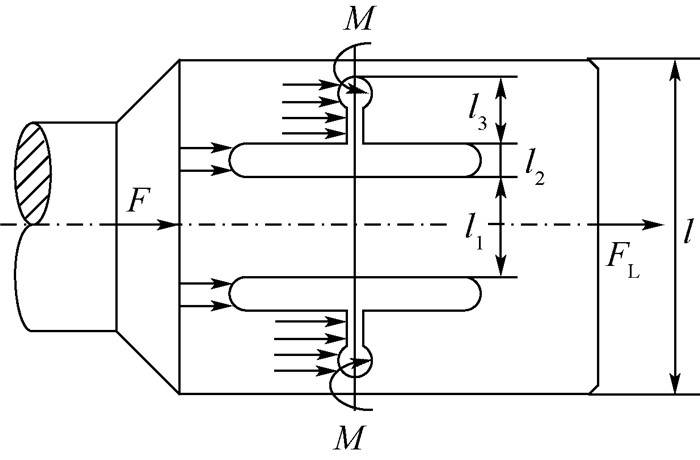 |
| 图 3 辐射头结构参数 Fig. 3 Structure parameters of radiation head |
| 图选项 |
辐射头纵向分振动阻抗为
 | (2) |
式中:ρ5、c5、k5和L5分别为辐射头的密度、纵波波速、波数以及特征长度;S5-1和S5-2分别为辐射头的最大和最小横截面积。
辐射头弯曲分振动阻抗为
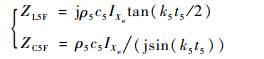 | (3) |
式中:t5为弯曲部分特征长度;IXe为弯曲横截面相对中性轴的惯性矩,其表达式为IXe=
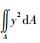
将各部分声阻抗代入图 2所示等效网络模型,可求出超声轴承的总声阻抗。阻抗模随频率变化曲线如图 4中虚线所示,超声轴承的最小阻抗频率 (即工作频率) 为16.020 kHz,最大阻抗模为33.330 kΩ。利用阻抗分析仪HP4294A对所设计的超声轴承样机声阻抗进行测试,可获得样机实际阻抗模曲线, 如图 4中实线所示,超声轴承的实际最小阻抗频率约为16.075 kHz,实际最大阻抗模值约为31.790 kΩ。对比结果显示,工作频率误差为0.34%,阻抗模误差为4.8%。轴承阻抗模的大小直接影响轴承与激励源的阻抗匹配,从而影响激励源的输出功率。经分析知,误差产生的主要原因是换能器电极层和黏接剂、材料参数以及结构尺寸误差等因素对超声轴承声阻抗的影响。
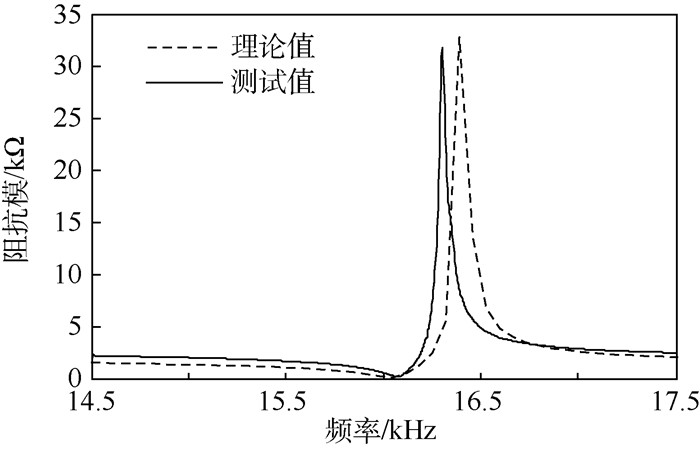 |
| 图 4 超声轴承声阻抗理论值与测试值 Fig. 4 Theoretical and testing values of ultrasonic bearing's acoustic impedance |
| 图选项 |
1.2 超声轴承输出振幅的测试 超声轴承的输出振幅是影响轴承悬浮特性的重要因素。借助激光位移传感器对所设计的超声轴承进行测试,可获得谐振频率下轴承凹面和侧面的输出振幅。经测试,超声轴承凹面输出稳定的正弦振动,侧面输出类正弦振动,其试验数据如图 5所示,在谐振频率下,超声轴承凹面的振幅峰峰值约为20 μm,侧面振幅峰峰值约为6.5 μm,纵弯振幅比约为3.08。
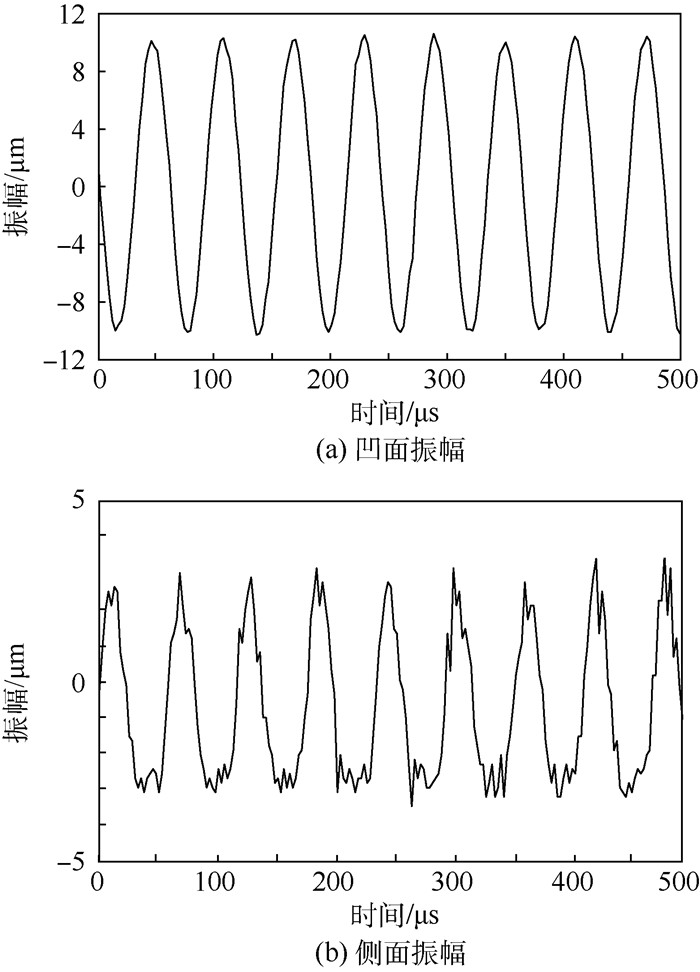 |
| 图 5 超声轴承凹面及侧面振幅 Fig. 5 Amplitudes of ultrasonic bearing at concave surface and lateral surface |
| 图选项 |
2 超声轴承有限元仿真 针对结构复杂的超声轴承的设计与优化,有限元法是一种行之有效的技术手段。通过有限元分析软件ANSYS中的静电-结构耦合场分析功能可对超声轴承的工作特性进行仿真计算。通过模态分析可获得超声轴承不同谐振频率下的模态振型,用于指导超声轴承重要结构参数的确定。通过谐响应分析可预测超声轴承在谐振工作频率下输出振动幅值,用以评估超声轴承的工作性能。
超声轴承中所用的压电陶瓷片上下表面具有一层很薄的银电极涂层,电极片的厚度仅为0.2 mm,有限元仿真过程中可不考虑电极片的影响,仅在模型中施加等电势边界以模拟电极的物理导电特性。实际工作过程中,由于机械损耗压电陶瓷片会逐渐发热,温升现象会对压电陶瓷的性能造成轻微的影响,仿真分析过程可忽略这一因素。
超声轴承的后盖板和预应力螺栓的材料为不锈钢SUS304,变幅杆材料为钛合金TC4。定义其单元类型均为8节点三维实体单元SOLID45;压电陶瓷材料为PZT-8,定义其单元类型为压电耦合场六面体单元SOLID5。SOLID5单元类型包含了机械和电学自由度。PZT-8压电陶瓷材料沿z轴方向极化的相对介电常数矩阵ε、压电常数矩阵e和弹性常数C矩阵分别为
 |
在频率区间0~40 kHz内,采用Block Lanczos方法对轴承模态进行搜索。一般情况下,超声轴承的纵振模态在前20阶范围内,因此,需提取前20阶模态进行计算。模态分析结果显示,超声轴承的一阶纵振模态频率为16 241 Hz,与实际工作频率的误差为1.03%。误差来源主要有建模过程中对结构的简化、压电陶瓷材料的机械损耗以及温升效应等。
超声轴承的一阶纵振模态如图 6所示,可清晰观察到轴承辐射端的振动变形。模态仿真结果充分证明沟槽结构成功将换能器输出的纵振转换成辐射头凹面纵振和侧面弯振。
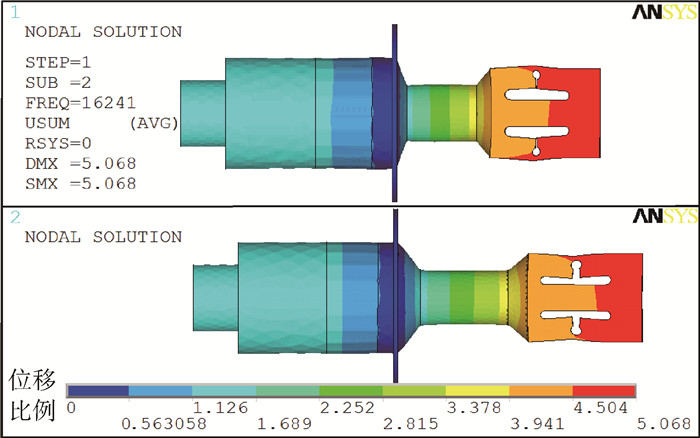 |
| 图 6 超声轴承工作模态 Fig. 6 Operating mode of ultrasonic bearing |
| 图选项 |
为进一步预测超声轴承辐射端输出振幅的大小,采用FULL运算方法,在16.0~16.5 kHz区间内,对有限元模型进行谐响应分析。仿真计算的步长设置为10 Hz;压电陶瓷激励电压设置为150 V。超声轴承辐射头凹面和侧面的最大振幅计算结果如图 7所示。凹面和侧面最大振幅分别约为12.0和3.5 μm,振幅比约为3.43:1。由于忽略了发热、结构阻尼和螺栓预紧力等因素对仿真结果的影响,因此,仿真结果比实际测量值略高。
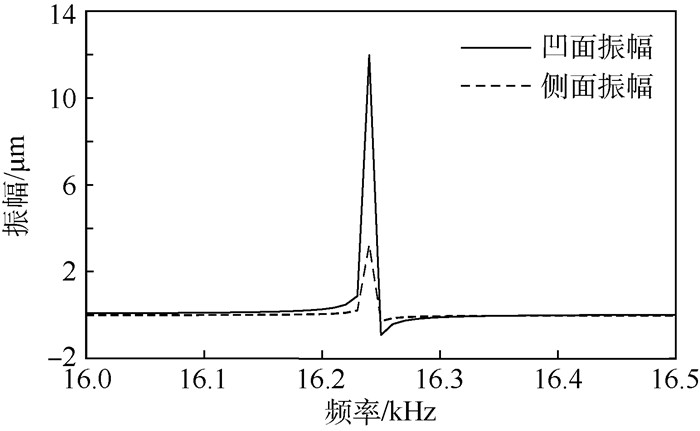 |
| 图 7 超声轴承输出振幅仿真结果 Fig. 7 Simulation results of ultrasonic bearing's output amplitude |
| 图选项 |
3 超声轴承悬浮承载力测试实验 3.1 超声轴承悬浮测试实验系统 超声悬浮轴承的测试实验系统由超声轴承样机、信号发生器、压电陶瓷驱动器、激光位移传感器、计算机、隔振实验台、支座和砝码等组成。测量原理如图 8所示。径向悬浮实验中,轴颈放在辐射头凹面中,通过更换轴颈两端的砝码改变悬浮重量;轴向悬浮实验中,只需将不同质量的平面物体放置在轴承辐射头侧面进行测量即可。径向和轴向悬浮测量时,超声轴承工作在谐振频率,激光位移传感器传感头发出的激光分别打在轴颈顶端母线上和平板物体表面。实验所采用的压电陶瓷驱动器最大输出电压为200 V,激光位移传感器再现性为0.02 μm。
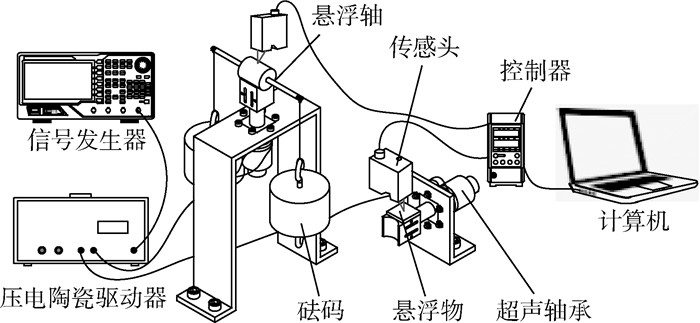 |
| 图 8 超声轴承悬浮承载力测量原理 Fig. 8 Measuring principle of ultrasonic bearing's levitating ability |
| 图选项 |
3.2 超声轴承径向与轴向悬浮实验 本文研制的超声轴承样机辐射端凹面直径为20.03 mm;选用的径向悬浮轴颈的直径为19.97 mm,质量约为23 g。辐射端凹面的表面粗糙度Ra值为0.8~1.6 μm。径向悬浮高度与悬浮质量曲线如图 9所示,当不加砝码,即悬浮质量为轴颈自重23 g时,径向悬浮高度可达85.2 μm;当悬浮质量为1 423 g时,径向悬浮高度约为12.1 μm。径向悬浮曲线表明,在工作频率和输出振幅固定条件下,随悬浮高度减小,超声轴承悬浮承载能力增加。悬浮高度在12~25 μm之间,承载能力随悬浮高度减小而急剧增加;当悬浮高度接近超声轴承凹面输出振幅值时,超声轴承承载能力最大。
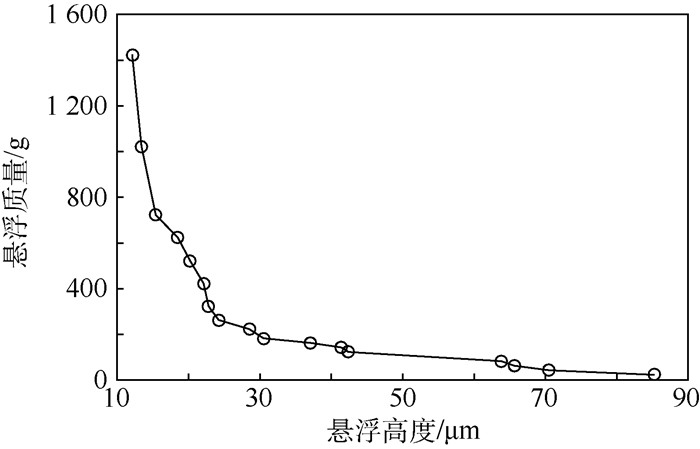 |
| 图 9 径向悬浮质量与悬浮高度的关系 Fig. 9 Relation between levitating mass and height in radial direction |
| 图选项 |
通过图 10所示曲线可清晰看出轴颈在悬浮过程中的运动情况。在轴颈两端各挂一个20 g砝码,1 s时刻时通电,历时约5 ms,轴颈便悬浮至最高点;经过约50 ms后,轴颈基本趋于稳定,在3.5 μm小范围内振荡。
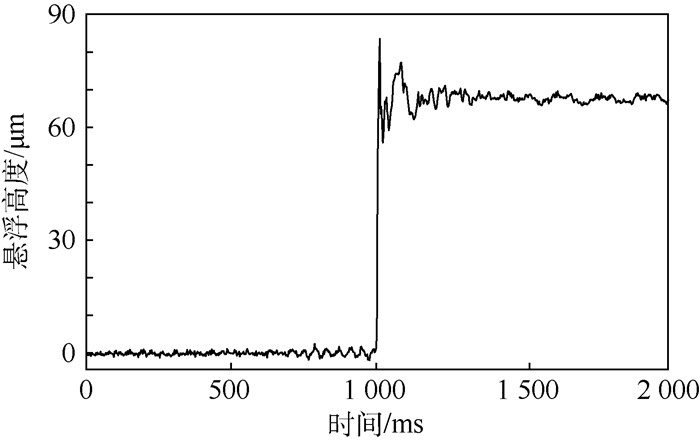 |
| 图 10 悬浮质量为63 g时的径向悬浮高度曲线 Fig. 10 Radial levitating height curve when levitating mass is 63 g |
| 图选项 |
轴向悬浮实验过程中,通过选择不同质量的悬浮物体改变悬浮质量。悬浮物上下表面粗糙度Ra值约为0.8 μm。实验中选用的悬浮物的质量分别为10、20、30、50、80、100、120、150和180 g。如图 11所示,经多次测量,悬浮高度的平均值分别为4.5、4.0、4.2、4.2、3.5、3.7、3.8、3.6和3.5 μm。图 12所示为悬浮物为20 g时,超声轴承轴向悬浮高度曲线。超声轴承的轴向悬浮高度约为侧面弯曲振动的振幅值。当悬浮质量达到一定值,悬浮物体将与轴承接触。由于超声轴承侧向为高频弯曲振动,即使轴承与承载物体发生接触,超声轴承在支承过程中也会产生超声减摩的作用。
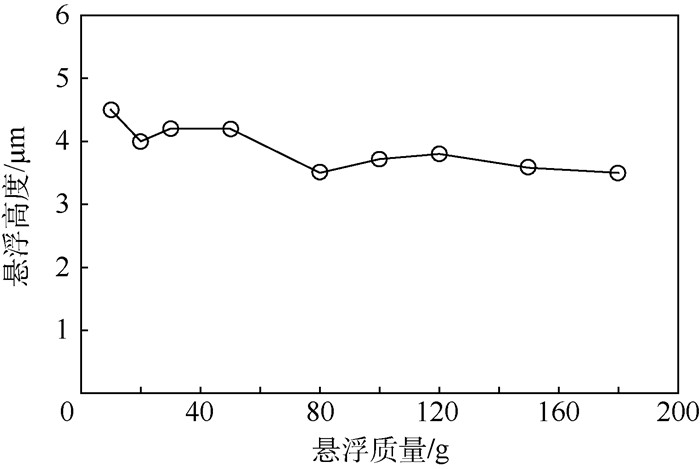 |
| 图 11 轴向悬浮质量与悬浮高度的关系 Fig. 11 Relation between levitating mass and height in axial direction |
| 图选项 |
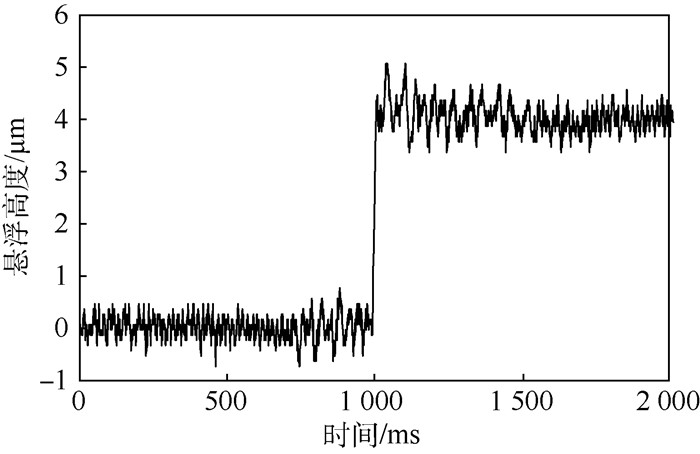 |
| 图 12 悬浮质量为20 g时的轴向悬浮高度曲线 Fig. 12 Axial levitating height curve when levitating mass is 20 g |
| 图选项 |
4 结论 1) 基于压电驱动原理和超声波近场悬浮技术,提出了一种超声悬浮轴承新结构。此悬浮轴承利用辐射头的沟槽结构将部分纵振转换成弯振,实现了单个换能器作动下对径向和轴向载荷的支承。非接触状态下的径向和轴向悬浮力可达约15.0和1.8 N。若提高轴承支承面的表面加工质量或振幅,径向和轴向承载力仍有较大提升空间。
2) 通过建立超声轴承的声阻抗网络模型,确定了轴承工作频率和声阻抗;利用实验测量手段获得了轴承承载面输出振幅;借助有限元法,对超声轴承进行了模态和谐响应分析,可指导超声轴承构型设计,修正超声轴承重要结构尺寸参数。
3) 悬浮实验结果表明本文提出及研究的超声轴承具有同时承受径向和轴向载荷的能力。此类超声轴承的研究可为新型轴承结构的研发和探索提供参考借鉴。
参考文献
| [1] | IDE T, FRIEND J, NAKAMURA K, et al. A non-contact linear bearing and actuator via ultrasonic levitation[J].Sensors & Actuators A Physical, 2007, 135(2): 740–747. |
| [2] | 常颖, 吴博达, 杨志刚, 等. 超声波悬浮推力轴承承载能力及减摩性能[J].吉林大学学报, 2004, 34(2): 222–225. CHANG Y, WU B D, YANG Z G, et al. Bearing capacity and anti-friction behavior of ultrasonic vibration bearing[J].Journal of Jilin University, 2004, 34(2): 222–225.(in Chinese) |
| [3] | 田丰君, 车小红, 杨志刚, 等. 双向支撑超声波悬浮轴承的设计[J].光学精密工程, 2009, 17(4): 813–818. TIAN F J, CHE X H, YANG Z G, et al. Structure design of bidirectional support ultrasonic levitation bearing[J].Optics and Precision Engineering, 2009, 17(4): 813–818.(in Chinese) |
| [4] | 刘家郡. 超声悬浮/气浮的混合悬浮及其行波驱动机理及实验研究[D]. 长春: 吉林大学, 2013: 81-86. LIU J J. Research on principle and design of the driving based on near-filed acoustic levitation and pneumatic suspension[D].Changchun:Jilin University, 2013:81-86(in Chinese). |
| [5] | 王冬. 超声悬浮轴承及微小电机机械特性测试技术研究[D]. 南京: 南京航空航天大学, 2010: 25-27. WANG D.Research on ultrasonic suspension bearing and testing technology of micro-motor mechanical property[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2010:25-27(in Chinese). |
| [6] | CHEN C, WANG J S, JIA B, et al. Design of a noncontact spherical bearing based on near-field acoustic levitation[J].Journal of Intelligent Material Systems & Structures, 2013, 25(6): 755–767. |
| [7] | ZHAO S, TWIEFEL J, WALLASCHEK J. Design and experimental investigations of high power piezoelectric transducers for a novel squeeze film journal bearing[J].Active & Passive Smart Structures & Integrated Systems, 2009, 7288(53): 1–8. |
| [8] | ZHAO S, MOJRZISCH S, WALLASCHEK J. An ultrasonic levitation journal bearing able to control spindle center position[J].Mechanical Systems & Signal Processing, 2013, 36(1): 168–181. |
| [9] | YOSHIMOTO S, ANNO Y, SATO Y, et al. Float characteristics of squeeze-film gas bearing with elastic hinges for linear motion guide[J].JSME International Journal, 1997, 40(2): 353–359.DOI:10.1299/jsmec.40.353 |
| [10] | YOSHIMOTO S, KOBAYASHI H, MIYATAKE M. Floating characteristics of a squeeze-film bearing for a linear motion guide using ultrasonic vibration[J].Tribology International, 2007, 40(3): 503–511.DOI:10.1016/j.triboint.2006.05.002 |
| [11] | HA D N, STOLARSKI T A, YOSHIMOTO S. An aerodynamic bearing with adjustable geometry and self-lifting capacity. Part 1:Self-lift capacity by squeeze film[J].Proceedings of the Institution of Mechanical Engineers Part J:Journal of Engineering Tribology, 2005, 219(1): 33–39.DOI:10.1243/135065005X9682 |
| [12] | STOLARSKI T A. Acoustic levitation-A novel alternative to traditional lubrication of contacting surfaces[J].Tribology Online, 2014, 9(4): 164–174.DOI:10.2474/trol.9.164 |
| [13] | WANG C, AU Y H J. Study of design parameters for squeeze film air journal bearing-excitation frequency and amplitude[J].Mechanical Sciences, 2011, 2(2): 147–155.DOI:10.5194/ms-2-147-2011 |
| [14] | WANG C, AU Y H J. Levitation characteristics of a squeeze-film air journal bearing at its normal modes[J].The International Journal of Advanced Manufacturing Technology, 2012, 60(1): 1–10. |
| [15] | WANG C, AU Y H J. Comparative performance of squeeze film air journal bearings made of aluminum and copper[J].The International Journal of Advanced Manufacturing Technology, 2013, 65(1): 57–66. |
