本文针对这些问题研究并设计了一套近场辐射源定位系统,使其能够对近场辐射源高效率、高精度定位,同时实现设备的简化,降低设备的体积与成本。
1 系统模型 本文设计的单天线单通道运动合成虚拟阵元的近场定位系统分为2个部分:信号接收控制分系统和接收信号处理分系统。系统的工作原理如下:
本系统将单一的接收天线连接至单通道接收机上,信号接收控制分系统通过控制天线运动,形成虚拟直线阵列,进而接收空间中的电磁信号[8]。同时该系统通过控制单通道接收机的采样频率以及采样时间间隔等参数,结合天线运动产生的空间接收模型,实现了对辐射源信号的采样;接受信号处理分系统将采样的信息代入到相关定位算法中,最终实现对近场辐射源信号的定位。
单天线单通道近场定位系统结构如图 1所示。假设天线在一条直线轨道上运动,当运动距离到达d后天线停下进行K次采样,该采样点记为阵列天线的等效阵元位置,如图 1中黑点所示。天线沿该直线运动形成M个等效阵元,称虚拟阵列阵元数为M。该阵列对近场单频连续波信号源s0(t)进行接收,信号源的频率为f0,波长为λ0,信号源与参考阵元1的法向夹角为θ,并且到参考阵元1的距离为r。天线通过单一通道接收信号,后再将信号进行处理进而实现信号源定位。
 |
| 图 1 单天线单通道近场定位系统 Fig. 1 Single antenna and single channelnear-field location system |
| 图选项 |
在信号源定位的理论分析中,通常假设信源发射的信号是窄带信号,由本节可知,单天线运动至每一个等效阵元时均会进行K次采样,设每次采样间隔为ts,天线从一个阵元运动至另一阵元的时间为t0,两阵元间距为d,天线的运动速度为d/t0。
不同于实际阵列的远场定位,由于是单天线单通道运动虚拟阵列,且近场信号的到达波前为球面波,所以不同快拍,不同阵元接收到的信号之间的时间延迟不一样,这也就意味着相位延迟不为固定值。本文认为该延迟由3种因素造成[9]:采样时间因素、运动时间因素和阵元距离因素。将运动合成虚拟直线阵列接收的输入信号写为矢量形式如下,天线运动到第m个阵元进行第k次采样接收到的信号为
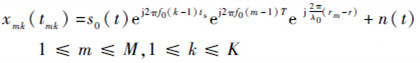 | (1) |
其中:
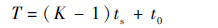 | (2) |
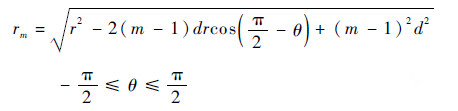 | (3) |
式中:rm 为发射源到m个虚拟阵元的距离,m=1,2,…,M,r1=r;tmk为天线运动到第m个阵元进行第k次采样所需要的时间;n(t)为噪声。
建立单天线运动虚拟阵列的系统模型后,可以利用MUSIC算法对信号进行角度估计,这是较常用的利用天线阵列进行定位的方法[10]。但是MUSIC算法定位通常需要确定待定位源的数量。同时利用MIUSIC算法进行定位时,为了满足信号与噪声的统计不相关特性,需要较大的快拍数。由于多快拍采样会带来更多的采样时间因素造成的延迟,而对其测量的精准程度对定位结果影响较大;更多的快拍数也会带来更大的数据量。在实际应用中,这些都限制了MUSIC算法定位的适用性。
压缩感知(CS)是近几年新兴起的一种信号采样理论[11]。它的思想是只要信号在某个变换域是稀疏的,就可以采用远低于奈奎斯特定律的采样率进行采样,根据算法由测量值重构原始信号[12]。
在MUSIC算法中,需要对被测区域进行空域的均匀采样。实际被测区域内只有少量位置上的信号是目标信号,其余位置上为无用的背景信号即冗余信息,如图 2所示。
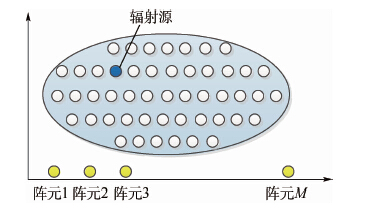 |
| 图 2 近场定位空间稀疏性示意图 Fig. 2 Schematic diagram of spatial sparsityof near-field location |
| 图选项 |
这表明目标信号在空间上是稀疏分布的。它满足压缩感知理论信号稀疏性的前提条件,因此可以利用压缩感知理论,用较少的采样数据对目标信号进行定位。
假设每个虚拟阵元上只进行一次采样。与MUSIC算法相比,一次采样由于不会产生每个虚拟阵元多次采样造成的采样时间间隔,因此可以不驻停采样,不会有因采样时间延迟因素可能引起的误差,提高了系统的适用性,同时可以大大减少数据量。
此时天线运动到第m个阵元时采样得到的关于目标信号空间向量的数据为
 | (4) |
式中:tm为天线运动到第m个阵元采样所需时间。
将被测区域与第一阵元的角度等量划分为i份,将被测区域与第一阵元的距离等量划分为j份,令 N=ij,代表了被测区域可能存在的目标位置数量,对应的目标信号空间向量S=[s1,s2,…,sN]T。
设空间中真实存在G个辐射源,NG。向量S中存在G个较大值,对应存在的G个目标信号,它的大小代表对应信号的幅度值,它的序号对应了接收信号与第一阵元的不同角度及距离。其余N-G个值代表无目标区域的背景噪声,较小或为0。根据式(4),阵列接收信号的数学模型为
 | (5) |
式中:X为M×1维矩阵,代表在M个虚拟阵列上不驻停采样得到的数据矩阵;Φ为M×N维测量矩阵,表示实际在M个虚拟阵元测量节点上进行了不驻停测量采样得到采样数据X;当第i(1≤i≤M)个监测节点所在的虚拟阵列序号为j(1≤j≤N),则Φ(i,j)=1,其余为0;ε为噪声矢量;A为N×N维矩阵,其定义为
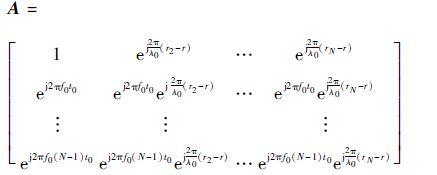 | (6) |
A表示向量S的阵列流行矩阵,相当于假设N个阵元的阵列对向量S采样,对向量进行了空间域的变换。
可以看出对于式(5)建立的线性方程组来说,根据压缩感知理论,可以通过一定的重构方法得到空间稀疏向量S中G个目标信号的位置与大小。
在已有的研究中,Candes和Tao[13]证明了信号重构问题是求解最小l0范数问题。而最小l0范数问题是一个非凸优化问题,要遍历所有可能的解,是NP-hard 问题,目前还没有较为有效的算法。但可通过求解最小化l1范数问题获得S的近似最优解。根据以上分析,利用接收到的单时刻阵列接收数据X,以及压缩感知算法,即可实现空间位置的定位,定义B=ΦA为恢复矩阵。定位模型:
 | (7) |
式中:σ为与噪声水平相关的参数。
这样,问题转化为一个凸优化问题,可以通过线性规划方法求解。正交匹配追踪(OMP)算法是较为常用的一种重构算法,它的原理是将求解稀疏向量S的问题转化为求解传感矩阵中参与组合过程的列的问题[14]。OMP保证了每次迭代的最优性,只要采样个数够多,它可以以较高的概率准确地重构信号[15]。
但是OMP的重构迭代搜索次数与稀疏度G相关,即需要已知稀疏度。在本文的应用中,稀疏度为目标信号的数量G。而定位问题针对的是未知目标源,既不知道目标位置,也不知道目标个数。本文提出对OMP算法进行改进,使其适用于目标数量未知的定位:设定以背景信号为阈值的迭代搜索终止条件。每次搜索使BS最接近X的单位稀疏阵,即X-BS最小的l稀疏阵,用X减BS,得残差X′,依次迭代搜索直到达到终止搜索条件即残差等于设定的背景信号阈值时。这时所有存在的目标就可以被搜索出,因此可以终止搜索。
2 仿真验证 依据第1节的系统理论模型,本文进行了仿真验证。设被测区域与第一阵元角度、距离分别为{-90°,90°}、{0.5 m,4.0 m}。被测目标频率为300 MHz,个数为1,角度相对于第一阵元为10°,距离为1.75 m,噪声设置为高斯白噪声,信噪比为20 dB。假设全向天线沿直线匀速运动,每隔距离d=0.5λ停下进行采样,λ为波长,停留次数即虚拟阵元个数为20,阵元间天线运动时间t0=5 s,每个虚拟阵元处的采样快拍数为10,采样时间间隔ts=1 s,利用MUSIC算法得到的定位结果如图 3所示。
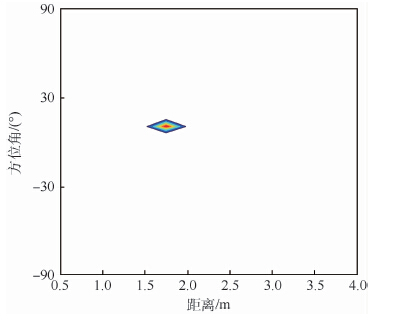 |
| 图 3 MUSIC算法定位结果 Fig. 3 Location result of MUSIC algorithm |
| 图选项 |
从仿真结果可以看到,对于目标的角度定位准确,表明运动虚拟阵列定位方法的系统模型构建正确。
将被测区域按5°的精度将被测区域与第一阵元的角度划分成36份,即Nθ=36;按0.25 m的精度将被测区域与第一阵元的距离划分为15份,即Nr=15,N=NθNr=540。假设已知存在一个目标信号,即向量的稀疏度G为1。设全向天线沿直线匀速运动不驻停,其余条件不变。因为阵元间天线运动时间t0=5 s,采样时间间隔ts=1 s,天线运动匀速不驻停,因此每隔5个采样结果取1个即为虚拟阵元位置处采样结果。利用压缩感知结合OMP算法得到的定位结果如图 4所示。
 |
| 图 4 压缩感知算法定位结果 Fig. 4 Location result of compressive sensing algorithm |
| 图选项 |
从仿真结果可以看出,同MUSIC算法一样,此算法也可以较好地定位目标源的角度,但是它并没有在每个阵元处驻停并多次采样,相当于在每个虚拟阵列上只进行一次测量,消除了式(1)中由采样延迟时间因素造成的相位误差,且所需数据量远远小于MUSIC算法。
将被测区域的目标信号个数改为3个,角度与距离相对于第一阵元分别为{-10°,10°,35°}、{2.25 m,1.75 m,3.00 m}。假设目标信号个数未知,其余条件不变。利用压缩感知结合本文改进后的信号重构方法得到的定位结果如图 5所示。
从仿真结果可以看出,利用改进后的信号重构方法可以较准确地估计目标信号个数与位置。
 |
| 图 5 信号源数目未知时的定位结果 Fig. 5 Location results when number of sources is unknown |
| 图选项 |
根据压缩感知理论,对于固定稀疏度G的N维离散信号S,测量节点数量M≥Glb$\left( {{N \over G}} \right)$时,可以以极大概率恢复稀疏向量。本文在不同的节点数量设置下进行多次仿真实验,统计其成功概率。
设一次实验中成功估计信号源个数以及信号角度估计偏差小于设置阈值时即为本次实验成功。定位成功率为实验成功次数占总实验次数的比例,即
 | (8) |
其中:
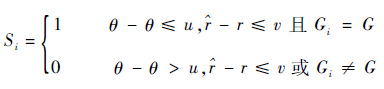 | (9) |
式中:Si的值表示在某节点数量条件下1次实验中是否能成功定位;θ^为此次定位所得的目标与第一阵元的角度;u为定位角度偏差阈值,设u=5°;为此次定位所得的目标与第一阵元距离;v为定位距离偏差阈值,设v=0.25 m;Gi为此次定位所得目标源个数;W为实验次数,设W为100次。
从图 6所示结果可知,在此实验中当测量节点数大于一定数量时,本文方法的定位估计成功概率较高,可以很好地完成近场定位功能。经过仿真实验可以看出本文方法符合理论推导,具有可行性。
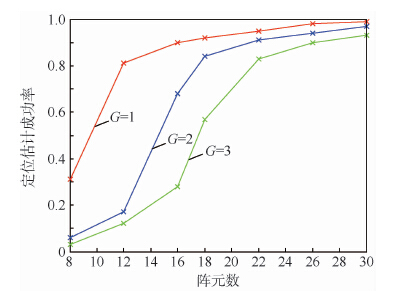 |
| 图 6 不同目标源数量在不同虚拟阵元数下的定位成功率 Fig. 6 Location success rate of different source quantity under different amount of virtual array elements |
| 图选项 |
3 系统设计与实验 为了使该定位系统能够应用于实际测试,本文设计了信号接收控制分系统,实现了近场定位系统中对空间信号源的接收。通过对信号接收控制分系统硬件构成以及软件部分的设计与研究,搭建了能够使近场定位系统正常运转的控制系统,满足了定位系统结构简单的需求,同时实现了设备稳定、自动化的接收。
控制系统分为3个部分:总体控制模块、信号接收模块以及天线运动模块,如图 7所示。
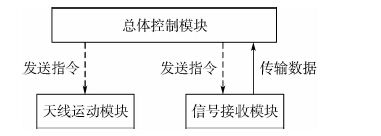 |
| 图 7 控制系统模块图 Fig. 7 Control system module diagram |
| 图选项 |
控制系统由总体控制模块发出指令,控制天线运动模块运作;将天线沿直线导轨运动到虚拟阵元处后,总体控制模块向信号接收模块发出指令,使得信号接收模块开始对空间辐射信号源进行采样;利用MUSIC算法时,当采样数据的数量达到要求,信号接收模块将数据传输至总体控制模块进行存储。此时总体控制模块将会判断天线是否运动并停留次数到达所需阵元数:若否,则继续控制天线运动以及进行信号接收;若是,则测试结束。利用压缩感知算法时,信号接收模块持续采样并将数据传输储存。
利用设计搭建的信号接收控制分系统进行实际测试。被测区域为{-45°,45°},{0.25 m,3 m}。被测目标频率为900 MHz,个数为1,信号功率为-10 dB·m,角度相对于第一阵元为30°。距离r为1.25 m。信噪比为20 dB,虚拟阵元距离d=0.5λ。控制全向天线沿直线匀速运动,速度为10 m/min,阵元间天线运动时间t0=1 s,采样时间间隔ts=1 s,每处虚拟阵元处采样10次。并将被测区域与第一阵元距离角度以测量精度5°划分为18份,与第一阵元距离以测量精度0.25 m划分为11份。分别利用MUSIC算法以及本文改进后的压缩感知算法在不同的虚拟阵元数M=5,10,12,16,20,24,28条件下进行多次定位实验,每个M值下各实验W=20次。定义定位误差公式为
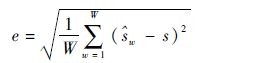 | (10) |
式中:${{\hat s}_w}$为一次实验得到的源的位置;s为源的实际位置。对比MUSIC算法与本文改进后的压缩感知算法定位的误差,如图 8所示。
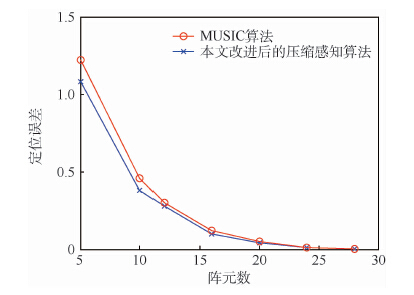 |
| 图 8 不同算方法下的定位误差 Fig. 8 Location error of different algorithms |
| 图选项 |
通过实验及误差统计可以看出,本文提出的基于单天线运动虚拟阵列的近场定位系统在实际实验中,当测量节点达到一定数量时,可以较好地完成定位。且本文提出的利用信号稀疏性来估计未知信号位置的方法较MUSIC算法相比具有更少的延迟因素,且所需采样数据大大减小。在实验中,同样阵元数的情况下,本文所需采样数据仅为MUSIC算法的1/10。
4 结 论 1) 本文提出了一种单天线运动合成阵列的近场辐射源定位方法,可以估计未知信号源的数量并定位。
2) 本文提出方法与常用的MUSIC算法相比,在保证定位精度的同时,极大减少了采样数据,以及采样时间可能带来的误差。
3) 经过设计搭建定位系统,在实际环境下多次实验,结果表明本文设计的系统具备近场定位能力,对于近场条件下的电磁辐射干扰源检测定位具有一定的参考意义及实用价值。
参考文献
| [1] | 刘尚合, 孙国至. 复杂电磁环境内涵及效应分析[J].装备指挥技术学院学报, 2008, 19(1): 1–5.LIU S H, SUN G Z. Analysis of the concept and effects of complex electromagnetic environment[J].Journal of the Academy of Equipment Command & Technology, 2008, 19(1): 1–5.(in Chinese) |
| [2] | CERRI G, DE L R, DELLA N L, et al. Fault location on shielded cables:Electromagnetic modelling and improved measurement data processing[J].IEE Proceedings-Science, Measurement and Technology, 2005, 152(5): 217–226.DOI:10.1049/ip-smt:20045035 |
| [3] | KODALI V P.工程电磁兼容:原理、测试、技术工艺及计算机模型[M].陈淑凤,高攸纲,苏东林,等译.北京:人民邮电出版社,2006:156-162.KODALI V P.Engineering electromagnetic compatibility:Principles,measurements,technologies,and computer models[M].CHEN S F,GAO Y G,SU D L,et al,translated.Beijing:People's Posts and Telecommunications Publishing House,2006:156-162(in Chinese). |
| [4] | 贾翠霞. 电子信息系统电磁兼容性测试研究[J].中国电子科学研究院学报, 2005(2): 33–36.JIA C X. Research on electromagnetic compatibility testing of electronic information system[J].Journal of China Academy of Electronics and Information Technology, 2005(2): 33–36.(in Chinese) |
| [5] | MICHEL M.电磁干扰排查及故障解决的电磁兼容技术[M].刘萍,魏东兴,藏瑞华,等译.北京:机械工业出版社,2002:27-30.MICHEL M.Electromagnetic interference and electromagnetic compatibility technology troubleshooting[M].LIU P,WEI D X,ZANG R H,et al,transtated.Beijing:Mechanical Industry Publishing House,2002:27-30(in Chinese).http://www.doc88.com/p-0416182206859.html |
| [6] | MARTINEZ-LORENZO J A, RAPPAPORT C M, QUIVIRA F. Physical limitations on detecting tunnels using underground-focusing spotlight synthetic aperture radar[J].IEEE Transactions on Geoscience & Remote Sensing, 2011, 49(1): 65–70. |
| [7] | 陈少刚,谢树果,叶知秋.单通道阵列近场信源定位方法研究[C]//第十二届全国电波传播学术讨论年会.新乡:中国电子学会,2013,28:404-407.CHEN S G,XIE S G,YE Z Q.Research on near field source localization for single channel array[C]//12th Chinese National Symposium on Radio Propagation.Xinxiang:Chinese Institute of Electronics,2013,28:404-407(in Chinese). |
| [8] | MARTINEZ-LORENZO J A, QUIVIRA F, RAPPAPORT C M. SAR imaging of suicide bombers wearing concealed explosive threats[J].Progress in Electromagnetics Research, 2012, 125(1): 255–272. |
| [9] | ZENG X Y,XIE S G,HAO X C,et al.A near-field radiation source localization method based on passive synthetic arrays using single channel receiver[C]//10th Academic Forum for Graduate Students at Beihang University.Beijing:Beihang University,2014. |
| [10] | 蔡晶晶, 鲍丹, 李鹏, 等. 强约束优化降维MUSIC二维DOA估计[J].电子与信息学报, 2014(5): 1113–1118.CAI J J, BAO D, LI P, et al. Two-dimensional DOA Estimation using reduced-dimensional MUSIC algorithm with strong-constraint optimization[J].Journal of Electronics & Information Technology, 2014(5): 1113–1118.(in Chinese) |
| [11] | BI D, XIE Y, LI X, et al. A sparsity basis selection method for compressed sensing[J].IEEE Signal Processing Letters, 2015, 22(10): 1738–1742.DOI:10.1109/LSP.2015.2429748 |
| [12] | 李珅, 马彩文, 李艳, 等. 压缩感知重构算法综述[J].红外与激光工程, 2013, 42(S01): 225–232.LI K, MA C W, LI Y, et al. Survey on reconstruction algorithm based on compressive sensing[J].Infrared and Laser Engineering, 2013, 42(S01): 225–232.(in Chinese) |
| [13] | CANDES E K, TAO T. Decoding by linear programming[J].IEEE Transactions on Information Theory, 2005, 51(12): 4203–4215.DOI:10.1109/TIT.2005.858979 |
| [14] | TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory, 2007, 53(12): 4655–4666.DOI:10.1109/TIT.2007.909108 |
| [15] | 白凌云, 梁志毅, 徐志军. 基于压缩感知信号重建的自适应正交多匹配追踪算法[J].计算机应用研究, 2011, 28(11): 4060–4063.BAI L Y, LIANG Z Y, XU Z J. Adaptive orthogonal multi matching pursuit algorithm for signal reconstruction based on compressive sensing[J].Application Research of Computers, 2011, 28(11): 4060–4063.(in Chinese) |
