Hesch和Betsch[2]成功地将Mortar法用来求解等几何分析中非协调问题,Mortar法实质是拉格朗日方法的一种。祝雪峰[3]也对Mortar法求解非协调问题做了相关研究。Nguyen等[4]基于Nitsche方法实现了三维实体的非协调网格等几何分析计算。Apostolatos等[5]将拉格朗日方法、罚函数法和Nitsche方法用在了二维平面非协调网格单元等几何分析中,并对比发现Nitsche方法在计算时要比前2种方法更加优越。Ruess等[6]基于有限胞元法对非协调以及裁剪模型进行了等几何分析。Guo和Ruess[7]研究了Kirchhoff-Love薄壳结构中的非协调等几何问题。Du等[8]对非协调Reissner-Mindlin板的静态弯曲问题进行了研究。但是,目前大部分的研究还是针对多张面片边界完全一致的情况,并没有考虑实际工程模型中面片边界存在缝隙和重叠的情况。
本文基于Nitsche方法研究面片边界不一致NURBS模型 (包括缝隙和重叠) 的等几何分析问题,并考虑其在Mindlin板弯曲和振动问题中的应用,对方法的收敛性、准确性等进行了验证。
1 多域问题描述与控制方程 1.1 多域问题描述 对复杂NURBS模型内部边界的处理,可以简化为对2张NURBS面片模型的处理。将每一张NURBS面片看作一个单独的域,现考虑以2-域为代表的多域线弹性边界值问题 (BVP)。如图 1所示,将三维空间域Ω分解为相连的两部分Ω1和Ω2,共同内边界记为Γ*,由于子域Ω1和Ω2在内边界处可能存在缝隙和重叠,内边界Γ*又分为Γ*1和Γ*2两部分。除去内边界Γ*,域其余边界又分为狄利克雷边界ΓD与纽曼边界ΓN,nm表示内边界上的外法向单位矢量, 上标m=1, 2代表不同的域空间。弹性动力学中,考虑内边界条件的BVP控制方程强形式表示为
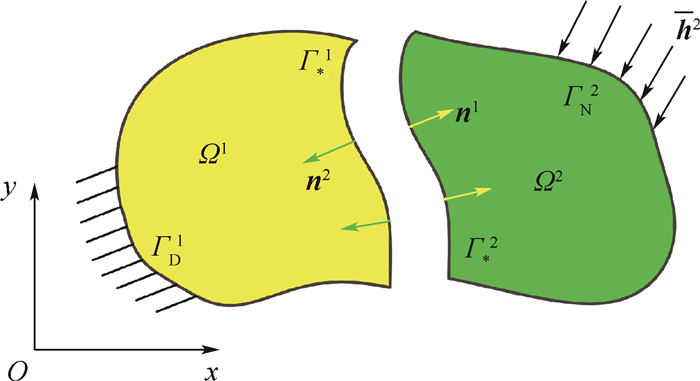 |
| 图 1 2-域问题示意图 Fig. 1 Schematic diagram of problem domain with two parts |
| 图选项 |
 | (1) |
 | (2) |
 | (3) |
 | (4) |
 | (5) |
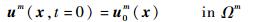 | (6) |
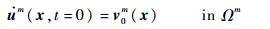 | (7) |
式中:?、σ、ρ和


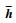
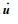
式 (1) 称为平衡方程,表示基于达朗贝尔原理表示的体积单元上的力平衡关系。式 (2) 和式 (3) 分别表示狄利克雷边界和纽曼边界上的位移和力边界条件。式 (4) 和式 (5) 用来建立不同域之间的变量关系,假定内边界外法线上位移和应力是连续的。式 (6) 和式 (7) 表示初始条件,位移、应力和应变等变量都是时间t的函数,假定t∈[0, T]。
根据弹性小变形理论,Mindlin板的广义应变张量ε可以表示为位移梯度函数:
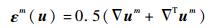 | (8) |
由胡克定律,应力场σ可以表示为
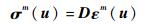 | (9) |
式中:D为根据材料属性得到的弹性系数矩阵,并且假定所有计算域Ω的材质均为线性各向同性。
1.2 Nitsche弱形式 定义试探函数空间Sm和权函数空间Vm,数学形式表示为
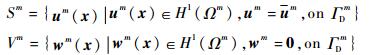 |
式中:H1为索伯列夫空间; w为试探函数。
假定边界条件是时间独立的,如果不考虑式 (4) 和式 (5) 描述的内边界上的约束条件,将权函数乘以平衡方程并进行分部积分可以得到BVP控制方程的变分形式,给定


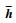
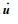
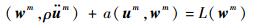 | (10) |
 | (11) |
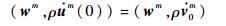 | (12) |
式 (10) 中的3项可具体表示为
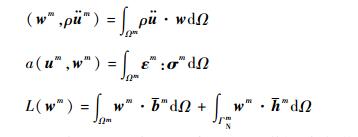 |
式 (10)~式 (12) 表示的是弹性动力学中的Galerkin弱形式,可以用来计算等几何分析中单张面片或者多张协调面片模型的动力学问题。当忽略式 (10) 中的加速度项时,方程可以用来求解静力学问题。
将式 (5) 和式 (6) 中的约束条件考虑在内,并对2-域模型中的交界面施加Nitsche方法弱约束[9-10],可以得到Nitsche弱形式控制方程:寻找u1, u2∈S1×S2,使得式 (13) 对所有w1, w2∈V1×V2成立。
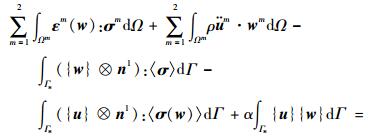 | (13) |
式中:等号左边第3~5项可以看作由Nitsche方法引入的变分项;大括号{·}和角括号〈·〉分别为阶跃算子与平均算子,其数学形式表示为
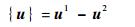 | (14) |
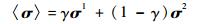 | (15) |
其中:参数γ为每一个子域的权重,且γ∈[0, 1], 本文中由于2个子域的材质等相同,取γ= 0.5。式 (13) 中参数α与罚函数中罚因子形式相同,但是意义差别很大,Nitsche方法中参数α可看作稳定因子。
2 等几何离散 2.1 NURBS及其基函数 单变量B样条基函数是由节点矢量构造出来的,节点矢量由参数空间中的一系列非递减坐标表示为Ξ={ξ0, ξ1, …, ξn+p+1},ξi为第i个节点值,i为节点索引号 (i=0, 1, …, n+p+1),p为多项式次数,n表示基函数的个数减1。如果节点矢量在节点序列两端具有p+1次重复度,则节点矢量为开 (open),开节点矢量是CAD中的标准节点矢量[11]。
对于p(p=1, 2, …) 次B样条曲线,根据Coxde Boor算法有
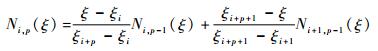 | (16) |
如果p=0, 有
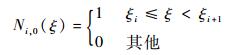 | (17) |
B样条基函数具有许多优良的特性可以引用在等几何分析中,如规范性、非负性和局部支撑性等。此外,B样条基函数可以在内节点处保持Cp-k连续,k表示节点重复度。高连续性将使等几何分析的计算结果更加精确。
假定一张NURBS曲面在2个参数 (ξ, η) 方向上的次数分别为p和q,节点矢量分别为
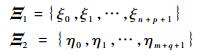 |
则NURBS曲面的数学形式表示为
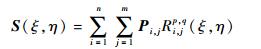 | (18) |
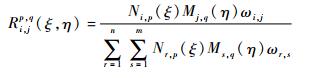 | (19) |
式中:n和m为曲面2个方向上的控制顶点数减1;N和M为参数方向上的B样条基函数;P为控制顶点;ω为控制顶点对应权重。
NURBS相关方法大部分都可以使用其对应的高一维的齐次空间的B样条来进行计算,但是NURBS的导数不能采用这一方法。本文使用R、X和W分别表示NURBS基函数、基函数的分子和分母。基函数R对ξ的一阶偏导数可以表示为
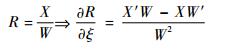 | (20) |
式中:
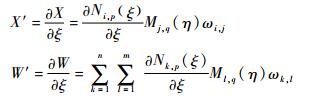 |
NURBS基函数的高阶导数可以通过相同的方式获得。节点插入算法和升阶算法是NURBS方法中的2个非常重要的算法,其在等几何分析中的作用相当于传统有限元中的h-型细化和p-型细化。等几何分析中的k-型细化是节点插入算法和升阶算法的有效结合。此外,徐岗等[12]还提出了基于最小化后验误差估计的r-型细化方法。
2.2 Mindlin板理论 相比于Kirchhoff理论对内部单元之间至少C1连续的要求,Mindlin假设弱化了对连续性的要求允许C0连续,且对薄板和厚板单元均适用。Mindlin理论考虑了剪切变形的影响,假定平板中面的直法线在变形后继续保持直线形状但不再垂直于中面[13]。在传统有限元计算中,当平板很薄时,使用Mindlin板理论计算容易产生剪切自锁,但是高阶连续的NURBS基函数却可以消除这一现象。
假定Mindlin板模型中面由二维参数域定义在x-y平面上,其几何描述以及坐标系统如图 2所示。图中:θx和θy分别为绕x轴和y轴的转角;w为z向挠度;h为板的厚度。材料属性定义如下:密度ρ、弹性模量E、泊松比ν和剪切模量G。位移的3个分量可以用数学形式表示为
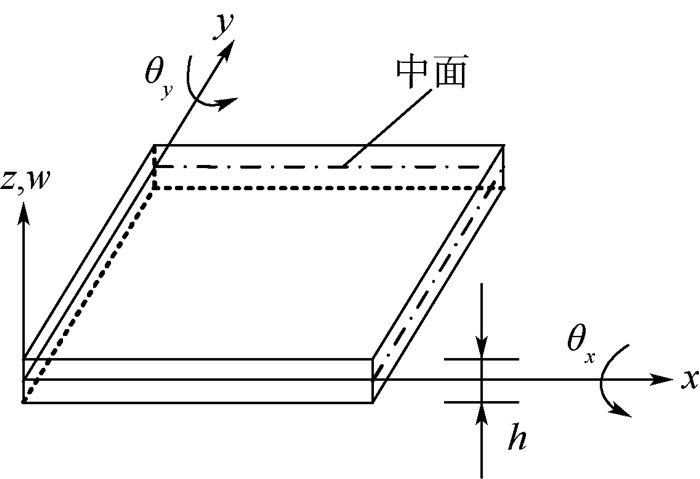 |
| 图 2 Mindlin板模型及其坐标系统 Fig. 2 Model and coordinate system of a Mindlin plate |
| 图选项 |
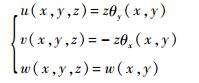 | (21) |
Mindlin板中广义应变εp可以表示为
 | (22) |
式中:κ和γ分别为弯曲应变和横向剪切应变,数学形式分别写为
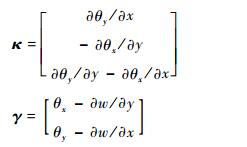 |
根据材料的本构关系,Mindlin平板的广义应力σp可以表示为
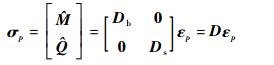 | (23) |
式中:
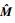
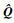
 |
其中:D0=Eh3/[12(1-ν2)]为平板的抗弯刚度;剪切模量G=E/[2(1+ν)];λ为剪切修正因子,取λ= 5/6。
2.3 离散方程推导 在等几何分析中,NURBS基函数被同时用来表示几何模型和逼近未知场变量。基于Mindlin板理论的几何模型和位移场的数学形式表示为
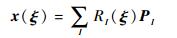 | (24) |
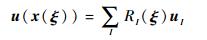 | (25) |
式中:RI为双变量NURBS基函数;PI和uI分别为控制顶点坐标和相应控制顶点的挠度。
由式 (21) 可知,Mindlin板中性面的位移可以表示为3个独立插值变量w、θx和θy的函数。位移矢量u可以写为
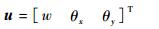 | (26) |
考虑NURBS单元上的各个变量关系,使用上标e来表示单元,则单元上的位移和加速度矢量可表示为
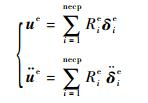 | (27) |
式中:δ和
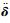
将式 (27) 表示成矩阵形式为
 | (28) |
将式 (28) 代入式 (22) 和式 (23),则单元广义应变和单元广义应力可以写为
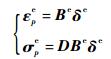 | (29) |
将式 (28) 和式 (29) 代入式 (10),并遍历所有单元组装整体刚度方程,可以得到基于动力学变分公式的离散方程为
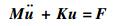 | (30) |
式中:M为质量矩阵;K为整体刚度矩阵;F为系统外载荷。
如果只考虑Mindlin板的静态弯曲问题,去掉式 (30) 等号左边的第1项即可得到静态弯曲的刚度方程,即
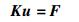 | (31) |
对于一个无阻力且无外载荷的动力学系统,离散方程可以简化为
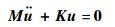 | (32) |
方程式 (32) 表示的振动形式为自由振动。将通解u=φneiωnt代入方程式 (32) 并改写为
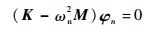 | (33) |
式中:φn为n-阶模态振型对应的n-阶自然频率ωn。
刚度矩阵K和质量矩阵M积分形式如下:
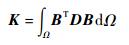 | (34) |
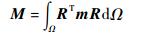 | (35) |
式中:B为几何函数矩阵;R为形函数矩阵;矩阵m表示为
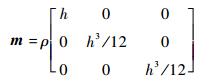 |
式 (33) 是自由振动的一般形式。如果考虑非相容板模型的动力学问题时,将式 (28) 和式 (29) 代入Nitsche弱形式控制方程式 (13),由此得到的Nitsche离散方程形式表示为
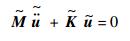 | (36) |
式中:质量矩阵
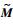
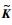
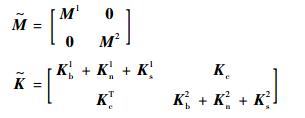 |
其中:Kbm、Knm和Ksm分别为体积刚度矩阵项、Nitsche项和稳定项;对称项Kc为耦合项。
体积刚度矩阵和稳定项分别表示为
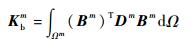 | (37) |
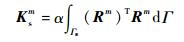 | (38) |
引用权重γ = 0.5,Nitsche项和耦合项可表示为
 | (39) |
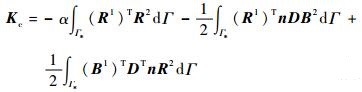 | (40) |
式中:外法向矢量n表示为
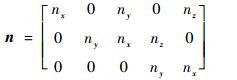 |
其中:nx、ny和nz为外法向单位矢量的3个分量。
2.4 交接面积分 由式 (37)~式 (40) 可知,稳定项、Nitsche项和耦合项都是在交界面Γ*上进行积分,对于Mindlin板模型来说,交界面是一条曲线。如果2张NURBS曲面在交界处完全一致,没有缝隙和重叠,只需要在该交界线上积分即可。对于存在缝隙和重叠的交界面,如图 3所示,首先选定1条主交界线 (如Γ*1),以主交界线作为积分线,遍历主交界线上的积分点,寻找与该积分点最近的次交界线Γ*2上的点,并反求其在子域中Ω2的参数。本文采用Newton-Raphson[11]方法来迭代求解映射点及其对应参数。由主交界线Γ*1上的积分点及其在次交界线Γ*2上的映射点即可求解沿交界线上的积分项Knm、Ksm和Kc。图 4给出了详细的求解整体刚度矩阵K的程序流程,左边部分表示各子域上的体积刚度矩阵Kbm的求解,右半部分表示各交界线上矩阵Knm、Ksm和Kcm的求解。对于求解Mindlin板静态弯曲问题,只需在求解Kbm的过程中加上等效节点载荷F的计算。求解自由振动问题,则需要在求解Kbm的过程中加上对质量矩阵M的计算。
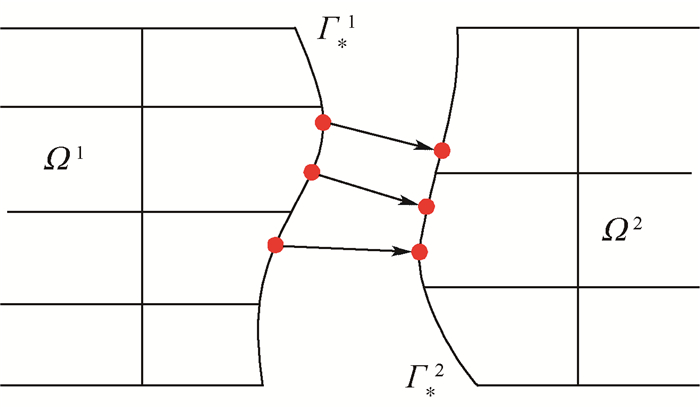 |
| 图 3 交界线Γ*1到Γ*2上的高斯点映射 Fig. 3 Mapping of Gauss points from interface Γ*1 to Γ*2 |
| 图选项 |
 |
| 图 4 求解整体刚度矩阵K程序流程图 Fig. 4 Program flowchart of solving global stiffness matrix K |
| 图选项 |
3 数值算例 以经典方板为例,研究非协调方板的静态弯曲和自由振动问题。如图 5所示, 方板由2张NURBS面片构成,圆点为NURBS控制顶点,实线为参数线。图 5(b)和图 5(c)分别为图 5(a)中上下2个黑框中图形的放大图,由放大图可知在方板模型中存在缝隙 (见图 5(b)) 和重叠 (见图 5(c)) 部分。2张NURBS面片的次数均为3×4次,单元数均为6×11,内部节点重复度均为1。方板的材料属性定义为:弹性模量E=200×109 N/m2,泊松比ν=0.3,密度ρ=8 000 kg/m3。算例中的稳定因子取值均为α=1×1014。
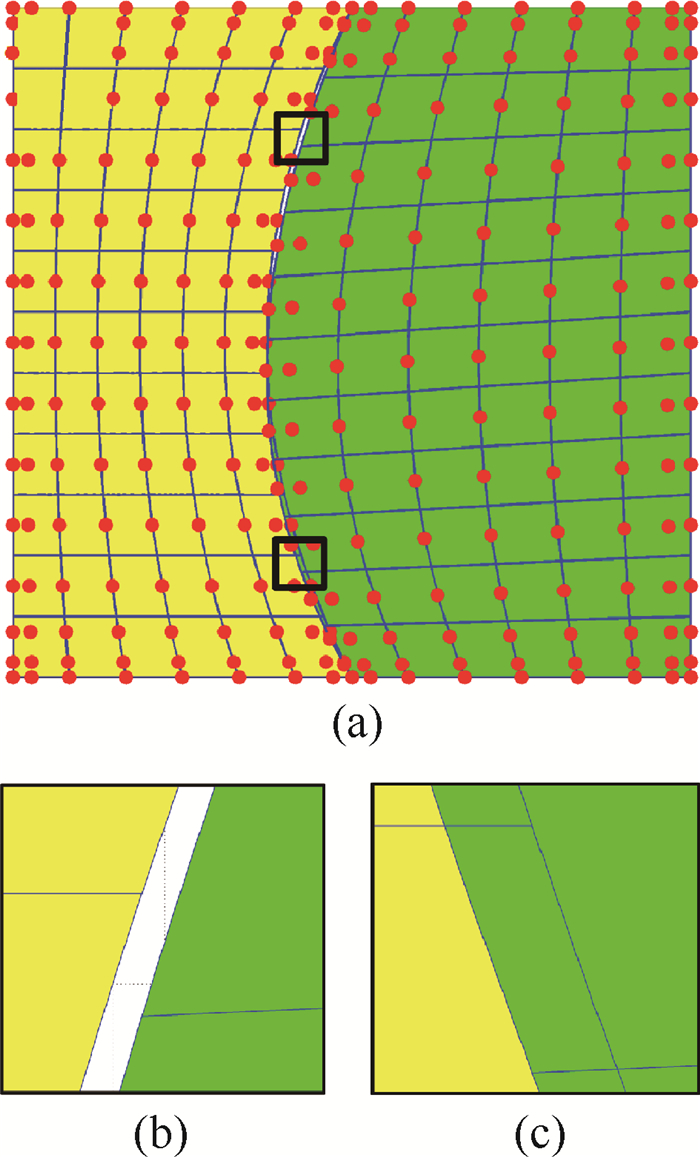 |
| 图 5 含缝隙与重叠部分的NURBS方板模型 Fig. 5 NURBS based square plate with gap and overlapping |
| 图选项 |
3.1 固支方板静态弯曲 研究方板的静态弯曲问题,方板四边固支,厚宽比h/l=0.1, 假定方板受到体积力f的作用。Chinosi和Lovadina[14]给出了本算例方板挠度和转角的解析解,Kiendl等[15]推导了该算例中方板的弯矩和剪切力的解析解。体积力f可表示为
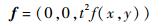 | (41) |
式中:
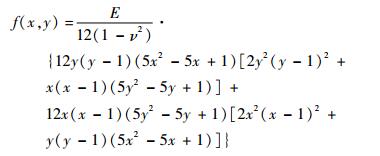 |
方板挠度的解析解可表示为
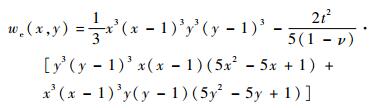 | (42) |
图 6给出了固支方板挠度的仿真结果,从图形上可以清晰地看到缝隙的存在。虽然在交界处存在缝隙与重叠,但是挠度在此处并没有出现大的波动。图 7给出了挠度的绝对误差, 可以看出,方板挠度的误差在交界线上达到最大,误差比挠度小2个数量级。
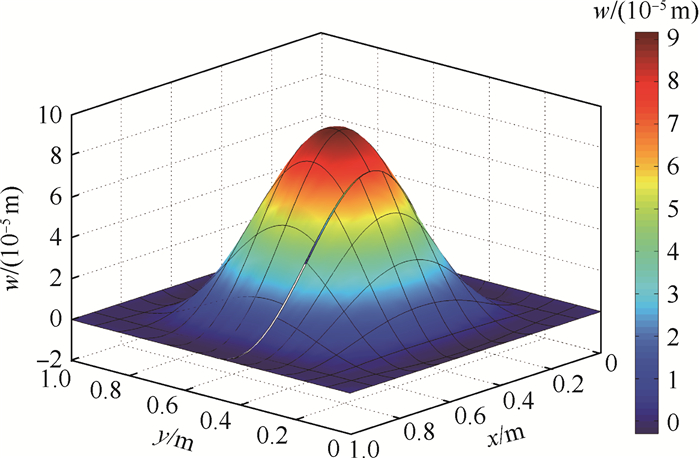 |
| 图 6 固支方板挠度 Fig. 6 Deflections of clamped square plate |
| 图选项 |
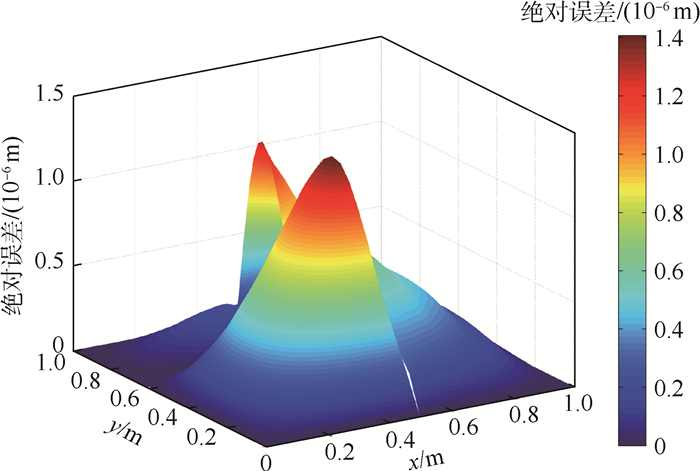 |
| 图 7 固支方板挠度绝对误差 Fig. 7 Absolute errors of deflection of clamped square plate |
| 图选项 |
3.2 固支方板自由振动 假定方板四边固支,研究方板在不同厚宽比h/l=0.1,0.2情况下的频率变化,并与Liew等[16]给出的精确解作对比。方板的无量纲频率参数可以表示为
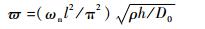 | (43) |
式中:ωn为方板的自然频率。
表 1给出了厚宽比h/l为0.1和0.2情况下的方板前10阶无量纲频率参数,与精确解保持一致, 厚度增大时频率降低。图 8绘制了不同次数 (p=q=2, 3, 4) 下的非协调方板前10阶模态频率参数的相对误差,p和q分别表示NURBS面片在2个方向上的次数,可以看出,随着次数的升高,误差逐渐降低。图 9给出了不同次数 (p=q=2, 3) 下的方板第1阶和第2阶频率参数的收敛图,纵坐标为频率相对误差
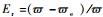
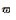
表 1 非协调固支方板频率参数 Table 1 Frequency parameters of non-conforming clamped square plate
| 模态阶数 | h/l=0.1 | h/l=0.2 | |||
| 等几何分析 | Liew等[16] | 等几何分析 | Liew等[16] | ||
| 1 | 3.297 0 | 3.295 4 | 2.688 4 | 2.687 5 | |
| 2 | 6.270 5 | 6.285 8 | 4.680 9 | 4.690 7 | |
| 3 | 6.304 7 | 6.285 8 | 4.702 1 | 4.690 7 | |
| 4 | 8.810 6 | 8.809 8 | 6.298 6 | 6.298 5 | |
| 5 | 10.377 1 | 10.378 8 | 7.174 3 | 7.176 7 | |
| 6 | 10.484 3 | 10.477 8 | 7.278 3 | 7.275 9 | |
| 7 | 12.539 4 | 12.552 9 | 8.507 0 | 8.515 5 | |
| 8 | 12.570 0 | 12.552 9 | 8.522 7 | 8.515 5 | |
| 9 | 15.296 0 | 15.291 8 | 10.008 9 | 10.012 6 | |
| 10 | 15.305 7 | 15.291 8 | 10.017 7 | 10.012 6 | |
表选项
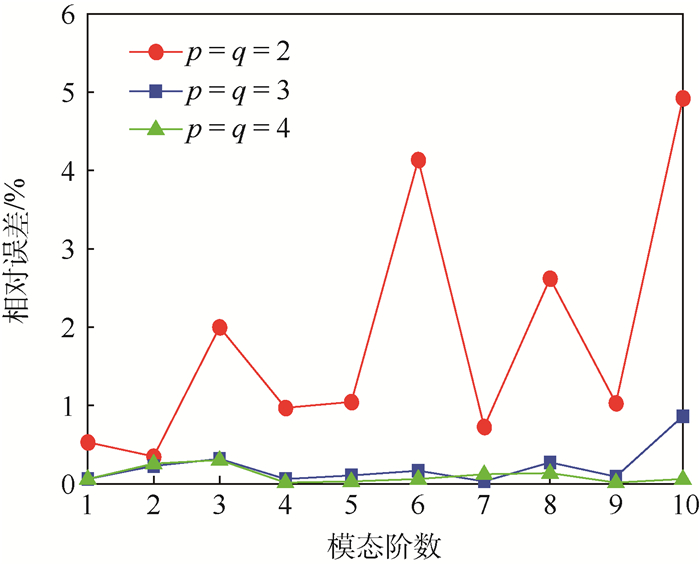 |
| 图 8 不同次数下的非协调方板前10阶频率相对误差 Fig. 8 Relative errors of first ten mode frequencies of non-conforming square plate with different polynomial degrees |
| 图选项 |
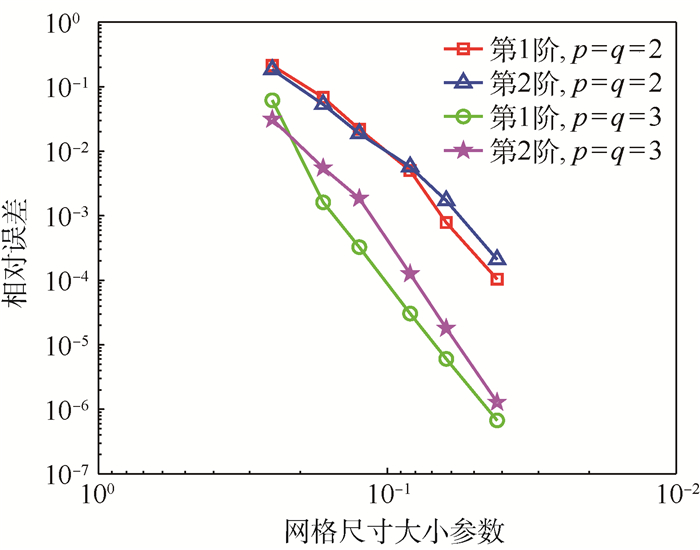 |
| 图 9 不同次数下的第1阶和第2阶非协调方板频率参数收敛 Fig. 9 Convergence of first two mode frequency parameters of non-conforming square plate with different polynomial degrees |
| 图选项 |
由图 9可知,次数越高,频率收敛速度越快,并且可以达到最优收敛。图 10给出了厚宽比h/l=0.1情况下方板的第1、4、6和12阶模态振型。
 |
| 图 10 非协调固支方板的模态振型 Fig. 10 Mode shapes of non-conforming clamped square plate |
| 图选项 |
4 结论 基于Nitsche方法对含缝隙和重叠部分Mindlin板的非协调等几何分析问题进行了理论研究,这一研究着眼于解决工程分析中常见的几何模型本身不完美而无法直接计算等几何计算的问题,对将等几何分析推广至更广范围内的工程应用具有重要价值。使用Mindlin板静态弯曲和自由振动的标准算例对本文方法的计算结果进行验证。结果表明:
1) Nitsche方法可以实现对含缝隙与重叠部分几何模型的等几何分析。
2) 推导的Mindlin板静态弯曲和自由振动刚度方程可以实现对平板挠度和转角以及自然频率进行预测。
3) NURBS次数越高,等几何分析的计算结果越精确。由于模型存在缝隙和重叠,计算结果与精确解会有一定误差。
4) 收敛性可以达到最优收敛,并且次数越高,收敛性速度越快。
为了使等几何分析更适用于工程模型分析,未来将研究几何拓扑等更复杂的模型,包括裁剪模型的等几何分析,并将推广本文方法在壳模型中的应用。
参考文献
| [1] | HUGHES T J R, COTTRELL J A, BAZILEVS Y. Isogeometric analysis:CAD, finite elements, NURBS, exact geometry and mesh refinement[J].Computer Methods in Applied Mechanics & Engineering, 2005, 194(s39-41): 4135–4195. |
| [2] | HESCH C, BETSCH P. Isogeometric analysis and domain decomposition methods[J].Computer Methods in Applied Mechanics & Engineering, 2012, 213(1): 104–112. |
| [3] | 祝雪峰. 复杂曲面非协调等几何分析及相关造型方法[D]. 大连: 大连理工大学, 2012.ZHU X F.Nonconforming isogeometric analysis for geometrically complex CAD surfaces and geometric modeling[D].Dalian:Dalian University of Technology, 2012(in Chinese). |
| [4] | NGUYEN V P, KERFRIDEN P, BRINO M, et al. Nitsche's method for two and three dimensional NURBS patch coupling[J].Computational Mechanics, 2014, 53(6): 1–20. |
| [5] | APOSTOLATOS A, SCHMIDT R, WVCHNER R, et al. A Nitsche-type formulation and comparison of the most common domain decomposition methods in isogeometric analysis[J].International Journal for Numerical Methods in Engineering, 2014, 97(7): 473–504.DOI:10.1002/nme.v97.7 |
| [6] | RUESS M, SCHILLINGER D, ?ZCAN A I, et al. Weak coupling for isogeometric analysis of non-matching and trimmed multi-patch geometries[J].Computer Methods in Applied Mechanics & Engineering, 2014, 269(2): 46–71. |
| [7] | GUO Y, RUESS M. Nitsche's method for a coupling of isogeometric thin shells and blended shell structures[J].Computer Methods in Applied Mechanics & Engineering, 2015, 284: 881–905. |
| [8] | DU X X, ZHAO G, WANG W. Nitsche method for isogeometric analysis of Reissner-Mindlin plate with non-conforming multi-patches[J].Computer Aided Geometric Design, 2015(s35-36): 121–136. |
| [9] | NITSCHE J. Vber ein variationsprinzip zur l sung von dirichlet-problemen bei verwendung von teilr?umen, die keinen randbedingungen unterworfen sind[J].Abhandlungen aus dem Mathematischen Seminar der Universit?t Hamburg, 1971, 36: 9–15.DOI:10.1007/BF02995904 |
| [10] | SANDERS J D, LAURSEN T A, PUSO M A. A Nitsche embedded mesh method[J].Computational Mechanics, 2012, 49(2): 243–257.DOI:10.1007/s00466-011-0641-2 |
| [11] | PIEGL L, TILLER W. The NURBS book[M].2nd edNew York: Springer, 1997. |
| [12] | XU G, MOURRAIN B, DUVIGNEAU R, et al. Parameterization of computational domain in isogeometric analysis:Methods and comparison[J].Computer Methods in Applied Mechanics & Engineering, 2011, 200(s23-24): 2021–2031. |
| [13] | ZIENKIEWICZ O C, TAYLOR R L. The finite element method for solid and structural mechanics[M].Singapore: Butterworth-Heinemann, 2005: 323-336. |
| [14] | CHINOSI C, LOVADINA C. Numerical analysis of some mixed finite element methods for Reissner-Mindlin plates[J].Computational Mechanics, 1995, 16(1): 36–44.DOI:10.1007/BF00369883 |
| [15] | KIENDL J, AURICCHIO F, VEIGA L B D, et al. Isogeometric collocation methods for the Reissner-Mindlin plate problem[J].Computer Methods in Applied Mechanics & Engineering, 2015, 284: 489–507. |
| [16] | LIEW K M, XIANG Y, KITIPORNCHAI S. Transverse vibration of thick rectangular plates-I.Comprehensive sets of boundary conditions[J].Computers & Structures, 1993, 49(1): 1–29. |
