航空工业对传动性能有着很高的要求，面齿轮传动作为一种实现相交轴运动和动力传递的新型传动方式^[1-2]，具有重量轻、结构紧凑、对轴向安装误差不敏感、分流效果好、承载能力高等优点，在航空领域具有广阔的应用前景，例如美国NASA已成功将面齿轮应用到某型直升机主减速器上^[3-6]，取得了良好的效果。
航空面齿轮必须使用硬齿面磨齿精加工以保证齿面精度和光洁度^[7]，在先前的粗加工阶段则可以采用插齿或滚齿方法。插齿加工刀具型面简单，制造成本低且修正容易，但是插齿效率比滚齿低。滚齿作为一种效率很高的齿轮加工方式，若能应用于面齿轮上，可以显著降低大批量面齿轮生产的时间成本。但是普通的阿基米德滚齿刀不能用于面齿轮的加工，需要对面齿轮专用的滚齿刀具进行研究。国外****^[8]最先提出了采用特殊滚刀加工面齿轮的思想，但通过滚齿加工得到的面齿轮齿面与理论偏差较大，精度上达不到要求。国内****对面齿轮滚磨刀具基蜗杆进行了研究^[9-12]，但其获得的型面方程复杂，且有奇异点限制，制造及修正难度大，刀具成本高。
球形滚刀作为对插齿刀的模拟，结构形式与阿基米德蜗杆滚刀相比有较大区别。对于球形滚刀，目前能够查阅到的相关研究较少。国内外研究人员对加工内齿轮的球形砂轮和球形滚刀进行了初步的研究^[13-18]，但其所提到的刀具基蜗杆的制造方法将会导致刀具法向具有一定的误差，利用这种球形砂轮或滚刀加工的面齿轮也将会有一定的型面误差^[19]。
本文参考面齿轮滚磨刀具基蜗杆和内齿轮球形滚磨刀具基蜗杆的设计方法，对面齿轮球形滚刀进行了研究，获得的刀具蜗杆的形式与之均不同，并对使用球形滚刀加工面齿轮进行了理论、仿真和试验研究，验证了面齿轮滚齿加工方法的正确性。本文对于面齿轮的高效滚齿加工具有一定的参考意义。
1 面齿轮齿面方程 面齿轮齿面的成形是基于圆柱直齿轮的插齿刀具与面齿轮展成切削得到的。面齿轮插齿刀的渐开线型面如图 1所示。图中：r_bs和r_ps分别为插齿刀渐开线基圆和节圆半径；θ_0s为插齿刀渐开线起始角度；θ_s为渐开线齿面的参数；β和γ分别代表渐开线的左右两支。

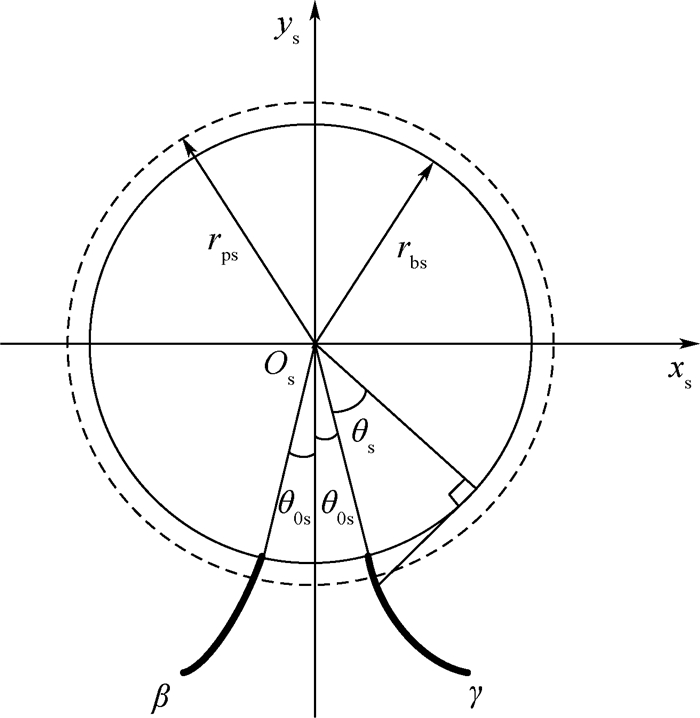图 1 面齿轮插齿刀渐开线齿廓 Fig. 1 Involute profile of face gear shaper's cutter tooth

图选项

插齿刀齿面方程为

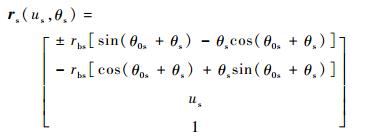(1)

式中：r_s为插齿口渐开线齿廓向量；u_s为渐开线齿面的另一参数；“±”号对应渐开线γ、β两支。
面齿轮成形可采用如图 2所示的坐标系：S_s(x_s, y_s, z_s)、S₂(x₂, y₂, z₂) 分别为与插齿刀、面齿轮固联的运动坐标系；固定坐标系S_s0(x_s0, y_s0, z_s0)、S₂₀(x₂₀, y₂₀, z₂₀) 分别为插齿刀、面齿轮的初始位置；δ为轴交角，正交面齿轮传动中取为90°。插齿刀绕z_s轴旋转角度Φ_s，面齿轮绕z₂轴旋转角度Φ₂，并且保持以下运动比例关系：

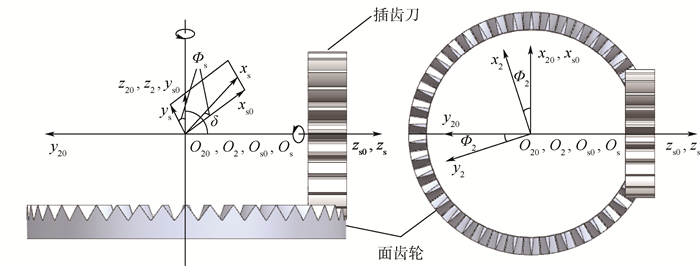图 2 面齿轮插齿加工坐标系 Fig. 2 Face gear shaping coordinate system

图选项

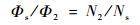(2)

式中：N₂和N_s分别为面齿轮和插齿刀齿数。
面齿轮通过插齿获得的型面方程可由坐标转换方程式 (3) 和啮合方程式 (4) 联立得到

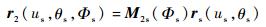(3)

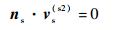(4)

式中: M_2s(Φ_s) 为从坐标系S_s到S₂的转换矩阵; n_s为刀具齿面的法向量; v_s^(s2)为在S_s坐标系上面齿轮与插齿刀的相对速度矢量。
2 面齿轮球形滚刀基蜗杆 2.1 球形滚刀基蜗杆的设计原理 与齿条向普通齿轮滚刀的演变类似，可以获得从圆柱齿轮向球形滚刀基蜗杆演变的过程。如图 3所示，设想在圆柱齿轮转动每一瞬时的截面，球形滚刀基蜗杆均有截面与之一样，那么球形滚刀基蜗杆转动起来在截面上就相当于圆柱齿轮在转动。圆柱齿轮与球形滚刀基蜗杆的转动比为N_w/N₀，其中:N_w为球形滚刀基蜗杆的头数，一般取为1;N₀为圆柱齿轮齿数，球形滚刀基蜗杆转动一圈，圆柱齿轮刚好转过一个齿。

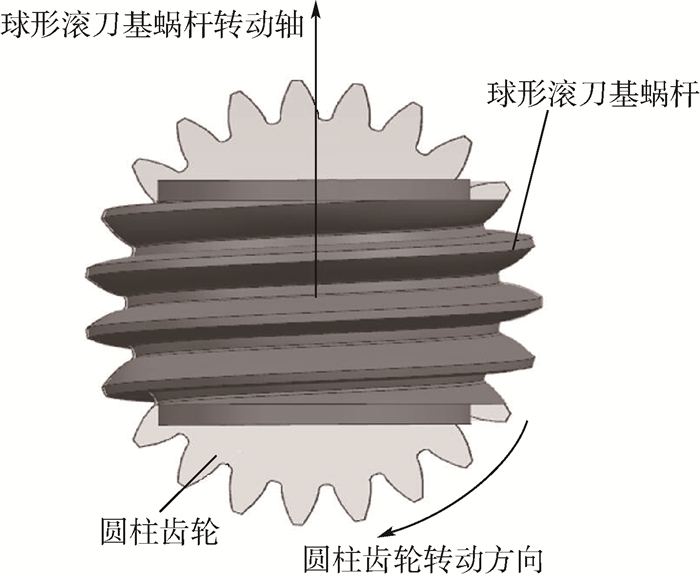图 3 球形滚刀基蜗杆演化 Fig. 3 Evolution of basic worm of spherical hob

图选项

球形滚刀基蜗杆的基圆球如图 4所示，x_nOz_n平面 (即Γ₁平面，也即法向剖面) 为xOz平面 (即Γ₂平面) 绕x轴转动角度λ得到，λ即为球形砂轮蜗杆的螺旋升角。Γ₁平面与基圆球相交产生一基圆，渐开线P₁A及P₂B均由此基圆得到，且2条渐开线关于x_n轴对称。P点为x轴与基圆球的交点，Q点为球面螺旋线上的一点，通过Q点可作垂直于z_n轴的端截圆平面。P₁A及P₂B绕z轴沿着球面螺旋线PQ进行旋转，即可得到球形滚刀的基蜗杆。

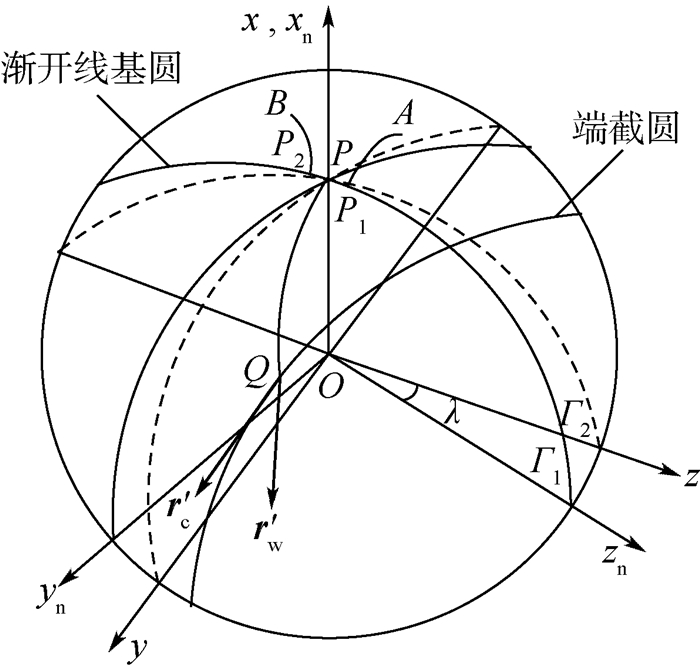图 4 球形滚刀基蜗杆的基圆球 Fig. 4 Basic sphere of basic worm of spherical hob

图选项

传统的球形滚刀基蜗杆的制造过程如图 5^[16]所示，滚刀毛坯在绕其轴线z旋转的过程中，具有特定齿廓形状的切削刀具 (齿形剖面位于Γ₂上) 以一定的转动比绕y轴在xOz平面内旋转，进行切削。这种制造方法得到的球面螺旋线轴向螺距相等，在轴剖面上齿形齿距是相同的，但法向螺距逐渐减小，法剖面上齿形齿距存在着一定的误差^[18]。另外，这种制造方法所用的刀具型面较为复杂^[15]，需要专门订做。

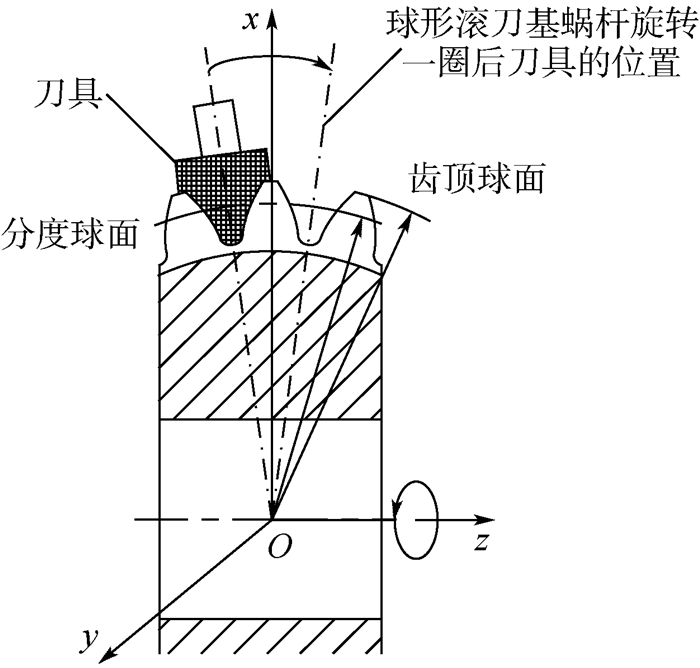图 5 球形滚刀制造方法 Fig. 5 Manufacture method of spherical hob

图选项

而实际上，切削刀具应该是绕着y_n轴在x_nOz_n平面内转动进行切削 (刀具正确的齿形剖面位于Γ₁上)，同时滚刀毛坯仍是绕z轴旋转，也就是刀具在法剖面内进行切削，这样球面螺旋线的法向螺距相等，从而获得在法向剖面具有正确渐开线齿形和齿距的球形滚刀基蜗杆，这种制造方法理论上在多轴联动机床上能够实现，而且所用的切削刀具剖面为标准的渐开线形状。
2.2 球形滚刀的基本蜗杆方程 以右旋为例，建立球形滚刀基蜗杆成形的坐标系如图 6所示。图中：S₀(x₀, y₀, z₀) 为固定坐标系；S_n0(x_n0, y_n0, z_n0) 为S₀绕x₀轴旋转λ角后所得的辅助固定坐标系; S_w(x_w, y_w, z_w) 为与球形滚刀基蜗杆固连的动坐标系; 绕z_w旋转角度设为φ_w；S_n(x_n, y_n, z_n) 为与切削刀具固连的运动坐标系；绕y_n旋转角度设为φ₀。φ_w和φ₀有以下运动关系：

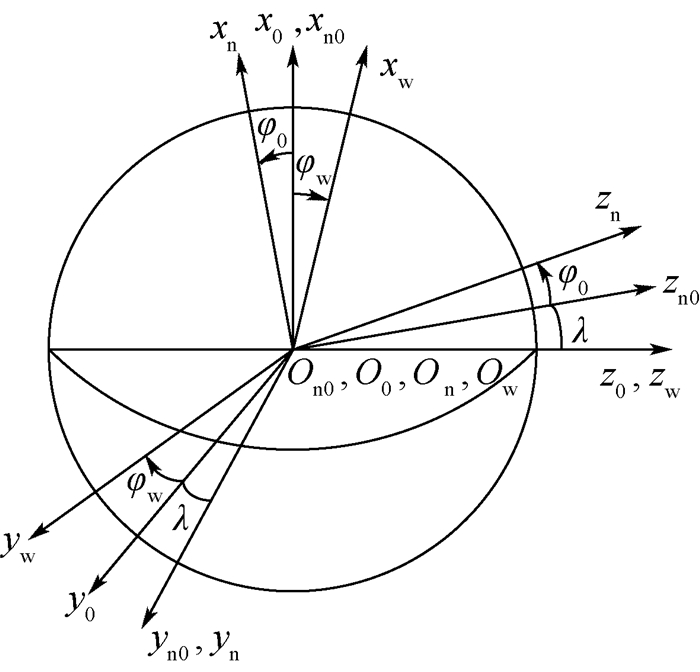图 6 球形滚刀基蜗杆成形的坐标系 Fig. 6 Coordinate system used for forming of basic worm of spherical hob

图选项

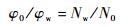(5)

转换矩阵分别如下：
M_{w, 0}为从S₀到S_w的转换矩阵，表达式为

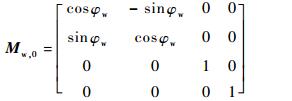(6)

Μ_{0, n0}为从S_n0到S₀的转换矩阵，表达式为

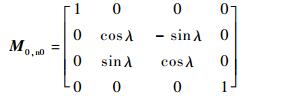(7)

Μ_{n0, n}为从S_n到S_n0的转换矩阵，表达式为

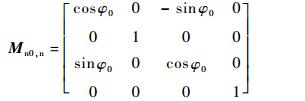(8)

在S_n中，渐开线方程表示为

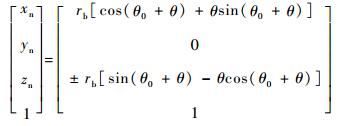(9)

式中:r_b为渐开线基圆半径；θ₀为渐开线起始角度；θ为渐开线参数。
则球形砂轮基蜗杆的方程如式 (10) 所示。其中：ξ=φ₀±(θ₀+θ)；“±”号对应基蜗杆的两侧面。

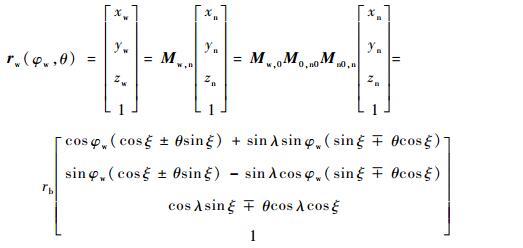(10)

2.3 球形滚刀基蜗杆的螺旋升角 球形滚刀基蜗杆的螺旋升角λ定义为螺旋线在Q点的切向矢量r′_w与过Q点的端截圆在Q点的切向矢量r′_c之间的夹角 (见图 4)，有

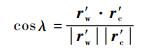(11)

为简化计算，可取螺旋线上的一点求取r′_s，在S_n坐标系中取 (a, 0, 0)，代入式 (10) 中并求导可得到

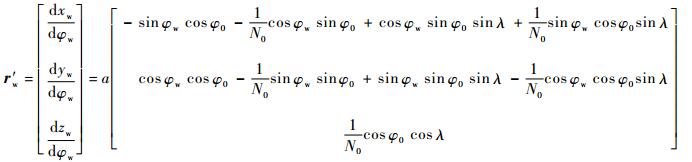(12)

端截圆的切向矢量为

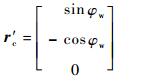(13)

当φ₀=0°时，联立式 (11)~式 (13)，将φ₀=0°代入即可求得此时的螺旋升角为

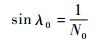(14)

此时的螺旋升角λ₀定义为球形滚刀基蜗杆的名义螺旋升角，也即球形滚刀的安装角。可见对应的圆柱齿轮齿数越多，球形滚刀基蜗杆的螺旋升角越小。
3 面齿轮滚齿加工型面方程 建立面齿轮滚齿加工坐标系如图 7所示。固定坐标系S_h0(x_h0, y_h0, z_h0) 为滚刀初始位置；S_h(x_h, y_h, z_h) 为与滚刀固联的运动坐标系；S_a(x_a, y_a, z_a) 为辅助坐标系，其绕x_a轴旋转λ₀角度即为S_h0坐标系。加工过程中，面齿轮的转角φ₂和滚刀的转角φ_h满足定比例关系：

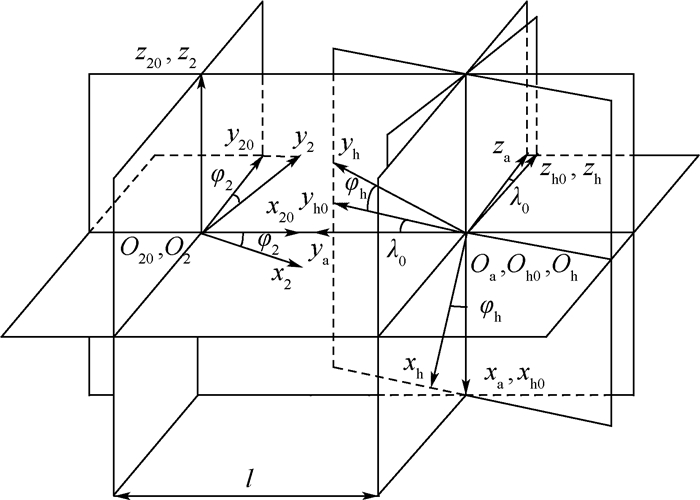图 7 面齿轮滚齿加工坐标系 Fig. 7 Coordinate system used for hobbing face gears

图选项

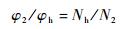(15)

式中：对单头球形滚刀，滚刀头数N_h=1。
转换矩阵分别如下：
M_{2, 20}为从S₂₀到S₂的转换矩阵，表达式为

(16)

M_{20, a}为从S_a到S₂₀的转换矩阵，表达式为

(17)

M_{a, h0}为从S_h0到S_a的转换矩阵，表达式为

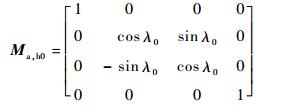(18)

M_{h0, h}为从S_h到S_h0的转换矩阵，表达式为

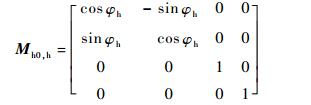(19)

则可得从S_h到S₂的转换矩阵为

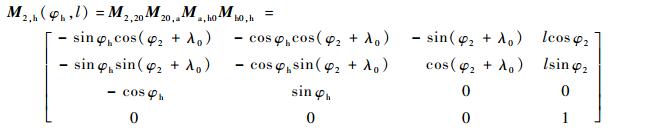(20)

那么，面齿轮齿面坐标转换方程为

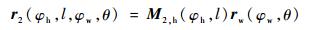(21)

同插齿刀加工面齿轮一样，根据啮合原理可以得到球形滚刀加工面齿轮的啮合方程式，由于滚刀除了与面齿轮保持定传动比外还需沿面齿轮径向进给，因此加工过程是双参数包络，即应同时满足：

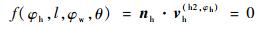(22)

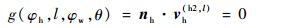(23)

其中：式 (22) 表示滚刀与面齿轮的相对旋转运动，v_h^{(h2, φh)}为l被固定住而φ_h运动时滚刀和面齿轮的相对运动速度；式 (23) 表示滚刀沿面齿轮的径向进给运动，v_h^{(h2, l)}为φ_h被固定住而l运动时滚刀和面齿轮的相对运动速度; n_h为滚刀齿面的法向量。
联立式 (21)~式 (23) 即可得到面齿轮的滚齿加工型面方程。
4 球形滚刀加工面齿轮仿真 以表 1所示2种参数的面齿轮为例，使用VERICUT软件对面齿轮球形滚刀滚齿加工进行仿真。
表 1 面齿轮基本参数 Table 1 Basic parameters of face gear

实例	面齿轮齿数	小齿轮齿数	模数/mm	压力角/(°)	齿长/mm
实例1	42	23	3.5	25	15
实例2	160	26	1.058 3	20	5

表选项






由于压力角25°的圆柱齿轮的根切最小齿数为12，而压力角20°的圆柱齿轮的根切最小齿数为17，因此与圆柱齿轮相对应的球形滚刀也不会发生根切。在实例1中毛坯宽度设置得比理论面齿轮齿长要长，从而验证面齿轮齿顶变尖和齿根根切现象。实例2所示参数的面齿轮已通过插齿加工实际应用于某型号飞机传动装置上，由于飞机空间有限，齿长受到限制，取面齿轮轮齿中间部分，长度为5 mm。
球形滚刀与面齿轮需要以固定的比例传动，因此在VERICUT软件G代码中添加指令“CGTECH_MACRO“GearModeOnOff”“1””。2个实例的安装角根据式 (14) 计算分别为2.492°和2.2°。
实例1仿真滚切结果如图 8所示，可以发现出现了面齿轮特有的根切及变尖现象。将滚齿加工所得模型与使用插齿加工获得的模型进行对比，最大误差仅为0.01 μm，误差产生的原因可能是刀具建模的精度及加工的包络残差造成的。实例2仿真滚切结果如图 9所示，与使用插齿加工获得的模型对比，最大误差为0.005 um。

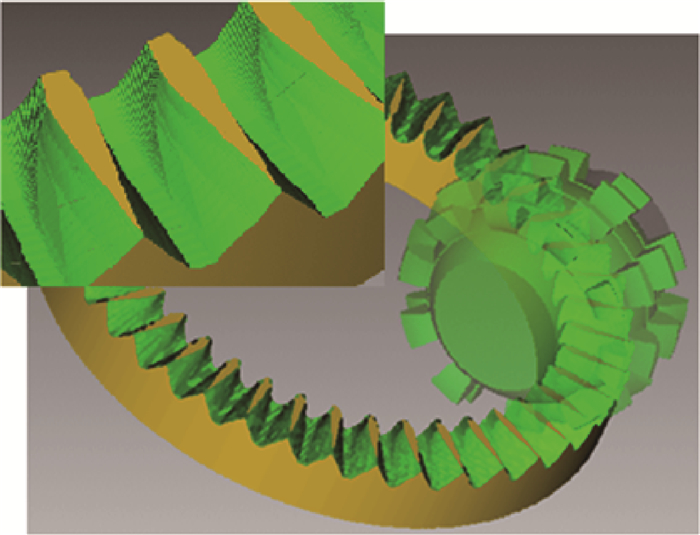图 8 实例1仿真滚切结果 Fig. 8 Result of hobbing simulation for Case 1

图选项

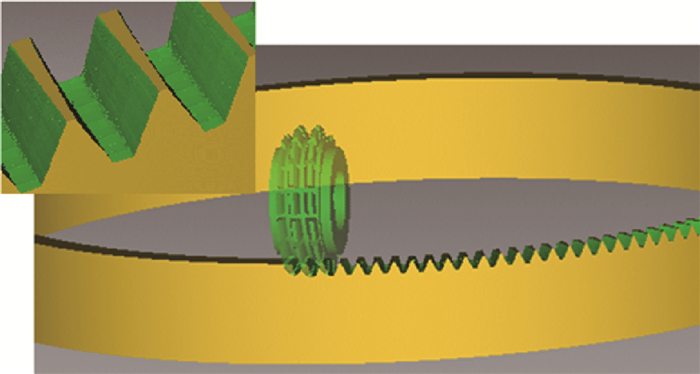图 9 实例2仿真滚切结果 Fig. 9 Result of hobbing simulation for Case 2

图选项

5 球形滚刀加工面齿轮试验 针对表 1中实例2所示参数的面齿轮，进行了球形滚刀的制造，并在面齿轮数控滚齿专用机床^[20]上进行了相应的面齿轮滚切加工试验，如图 10所示。在Wenzel三坐标测量机上对获得的面齿轮进行了检测，如图 11所示，得到其齿面点三维坐标值，经过坐标变换与理论坐标值进行对比，获得其齿面偏差图, 如图 12所示，最大误差为-44.3 μm。误差产生原因是刀具制造误差、机床误差和对刀误差综合所造成的。

图 10 球形滚刀实物图及面齿轮滚齿加工过程 Fig. 10 Photos of spherical hob and face gear hobbing process

图选项

图 11 面齿轮检测过程 Fig. 11 Face gear detection process

图选项

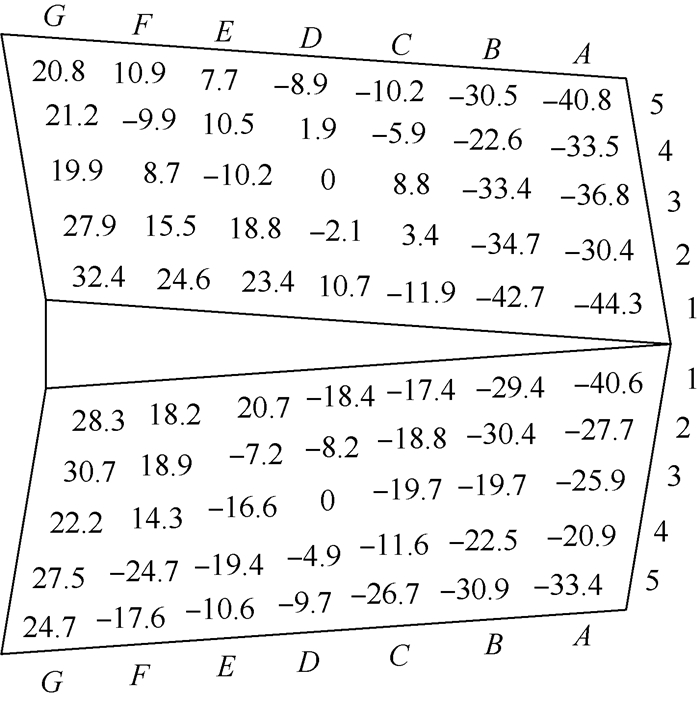图 12 面齿轮齿面法向偏差示意图 Fig. 12 Schematic of normal deviation of face gear tooth surface

图选项

6 结论 1) 阐述了球形滚刀的设计思想，以直观的方法推导了面齿轮球形滚刀的型面方程及螺旋升角；推导了球形滚刀加工面齿轮的过程，给出了面齿轮型面方程。
2) 对球形滚刀加工面齿轮进行仿真，结果表明与插齿加工相比齿面最大误差小于0.01 μm，验证了球形滚刀加工面齿轮的正确性。
3) 进行了滚齿加工试验，采用三坐标测量机对面齿轮精度进行了检测，检测结果表明齿面最大误差为-44.3 μm，检测结果验证了球形滚刀加工面齿轮的可行性。

参考文献

[1]	LITVIN F L, ZHANG Y, WANG J C, et al. Design and geometry of face-gear drives[J].Journal of Mechanical Design, 1992, 114(4): 642–647.DOI:10.1115/1.2917055
[2]	LITVIN F L, EGELJA A, TAN J. Computerized design, generation and simulation of meshing of orthogonal offset face-gear drive with a spur involute pinion with localized bearing contact[J].Mechanism and Machine Theory, 1998, 33(1-2): 87–102.DOI:10.1016/S0094-114X(97)00022-0
[3]	LITVIN F L, WANG J C, BOSSLER R B, et al. Application of face-gear drives in helicopter transmissions[J].Journal of Mechanical Design, 1992, 116(3): 672–676.
[4]	CHEN Y D, BOSSLER R B.Design, analysis, and testing methods for a split-torque face-gear transmission[C]//31st Joint Propulsion Conference and Exhibit.Reston:AIAA, 1995.
[5]	LEWICKI D G, HEATH G F, FILLER R R, et al.RDS-21 face-gear surface durability tests:ARL-TR-4089[R].Washington, D.C.:NASA, 2007.
[6]	HEATH G F, FILLER R R, TAN J.Development of face gear technology for industrial and aerospace power transmission:NASA/CR-2002-211320[R].Washington, D.C.:NASA, 2002.
[7]	WANG Y Z, LAN Z, HOU L W, et al. A precision generating grinding method for face gear using CBN wheel[J].International Journal of Advanced Manufacturing Technology, 2015, 79(9): 1839–1848.
[8]	MILLER E W.Hob for generating crown gears:US2304586[P].1942-12-08.
[9]	王延忠, 吴灿辉, 葛旭阳, 等. 面齿轮滚刀基本蜗杆的设计方法[J].北京航空航天大学学报, 2009, 35(2): 166–169.WANG Y Z, WU C H, GE X Y, et al. Basal worm designing method of face-gear hob[J].Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(2): 166–169.(in Chinese)
[10]	李政民卿, 朱如鹏. 面齿轮滚磨刀具基蜗杆研究[J].机械科学与技术, 2009, 28(1): 98–101.LI Z M Q, ZHU R P. A study of worm of hobbing or grinding wheel for face gear[J].Mechanical Science and Technology for Aerospace Engineering, 2009, 28(1): 98–101.(in Chinese)
[11]	高金忠, 朱如鹏, 李政民卿. 面齿轮滚磨刀具基蜗杆齿廓奇异点研究[J].航空动力学报, 2011, 26(10): 2394–2400.GAO J Z, ZHU L P, LI Z M Q. Research on singularities of base worm thread surface for hobbing or grinding face gear[J].Journal of Aerospace Power, 2011, 26(10): 2394–2400.(in Chinese)
[12]	郭辉, 赵宁, 项云飞, 等. 六轴数控蜗杆砂轮磨齿机磨削面齿轮的方法[J].机械工程学报, 2015, 51(11): 186–194.GUO H, ZHAO N, XIANG Y F, et al. Face gear grinding method using six-axis CNC worm wheel machine[J].Journal of Mechanical Engineering, 2015, 51(11): 186–194.DOI:10.3901/JME.2015.11.186(in Chinese)
[13]	王跃进. 球形滚刀螺旋面的研究[J].工具技术, 1990(1): 20–26.WANG Y J. Research on helicoidal surface of the spherical hob[J].Tool Technology, 1990(1): 20–26.(in Chinese)
[14]	崔云起, 胡占齐, 王尊策, 等. 球形滚刀的制造与理论误差[J].机械传动, 1994, 18(2): 55–58.CUI Y Q, HU Z Q, WANG Z C, et al. Manufacture and theoretical error of spherical hob[J].Mechanical Transmission, 1994, 18(2): 55–58.(in Chinese)
[15]	崔云起, 胡占齐. 球形滚刀的齿形[J].东北重型机械学院学报, 1995, 19(2): 100–103.CUI Y Q, HU Z Q. The profile of spherical hob[J].Journal of Northeast Heavy Machinery Institute, 1995, 19(2): 100–103.(in Chinese)
[16]	相浦正人, 广尾靖彰. 用球形滚刀滚切内齿轮[J].制造技术与机床, 1997(2): 13–16.AINOURA M, YASUSHIAKI H. Hobbing of internal gear with spherical hob[J].Manufacturing Technology and Machine Tools, 1997(2): 13–16.(in Chinese)
[17]	李宇鹏. 球形蜗杆砂轮的磨齿原理及其球基螺旋面参数[J].机械工程学报, 2002, 38(6): 127–129.LI Y P. Principle of grinding gear of spherical worm emerywheel and parameters of helicoid of spherical worm[J].Chinese Journal of Mechanical Engineering, 2002, 38(6): 127–129.DOI:10.3901/JME.2002.06.127(in Chinese)
[18]	郝哲. 球形滚刀设计及制造新工艺研究[D]. 秦皇岛: 燕山大学, 2013: 23-28.HAO Z.Design and new manufacture process study of the spherical hob[D].Qinhuangdao:Yanshan University, 2013:23-28(in Chinese).
[19]	赵宁, 郭辉, 方宗德, 等. 用球形滚刀滚切面齿轮的理论误差[J].航空动力学报, 2009, 24(3): 677–682.ZHAO N, GUO H, FANG Z D, et al. Theory error of cutting face gears with sphericity hob[J].Journal of Aerospace Power, 2009, 24(3): 677–682.(in Chinese)
[20]	王延忠, 侯良威, 郇极, 等. 一种面齿轮数控滚齿加工装置:CN102248228A[P].2013-02-13.WANG Y Z, HOU L W, HUAN J, et al.A kind of NC hobbing machine for face gear:CN102248228A[P].2013-02-13(in Chinese).