相较于单端面气膜密封,双端面气膜密封用于反转共轴结构中,可有效降低密封界面相对滑动速度;当密封系统受到扰动,双端面浮动式结构提高了密封系统的稳定性。目前,国内外对单端面气膜密封已有一定研究[5-9],针对反转轴间双端面气膜密封,Rolls-Royce公司提出了多种新型结构[10-11]并分析了其受力情况;国内对双端面气膜密封的稳态特性有一定的研究[3],但对反转轴间双端面气膜密封系统动特性的研究甚少。本文针对一种反转轴间双端面气膜密封系统,建立系统轴向力学平衡模型,采用有限元法求解气膜稳态压力分布与气膜反力。在此基础上,构建系统二自由度振动模型,施加瞬时力和持续激振力扰动,采用直接数值模拟法[12-14]耦合求解瞬态雷诺方程和动力学方程,研究双端面气膜密封系统自由振动和受迫振动的动力学响应。
1 密封结构及工作原理 密封系统采用双端面动静压混合止推环式密封结构设计,如图 1所示,图中PH为进口压力;PL为出口压力。主密封环与外转轴通过二次密封环实现密封。主密封环密封端面由两侧节流孔供气,密封端面气膜产生静压承载力,出口设计有浅腔,系统运行时浅腔的阶梯效应形成动静压混合。密封跑道前端面由波形弹簧支承,密封跑道与高压腔之间通过碳石墨环实现二次密封。
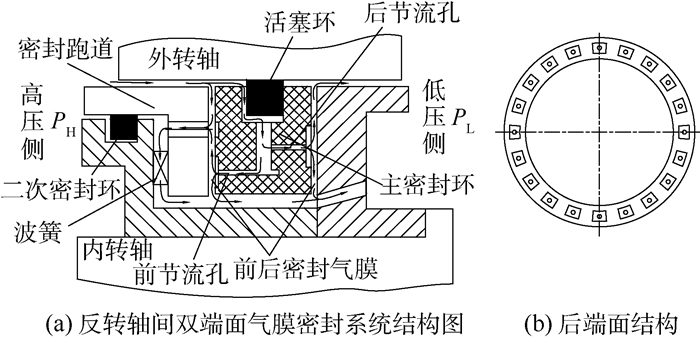 |
| 图 1 反转轴间双端面气膜密封系统 Fig. 1 Double-faced gas film seal system in counter-rotating intershafts |
| 图选项 |
密封系统工作时,高压气体经节流孔进入前后密封腔,气膜压力推动前密封跑道压紧波簧,当密封跑道和主密封环力系平衡后,密封系统达到稳态。
2 密封系统稳态求解 2.1 密封系统受力分析 当密封系统达到稳态时,前后端面气膜厚度为稳态气膜厚度记为hF0、hB0。密封跑道受左侧高低压气体压力FHL、前端面气膜力F(hF0)、弹簧力Fs及二次密封环摩擦力Ff1共同作用;主密封环受前后端面气膜反力F (hB0) 及活塞环与外转轴间的摩擦力Ff2共同作用,密封跑道和主密封环受力如图 2所示,其平衡条件为
 | (1) |
 | (2) |
式中:
 |
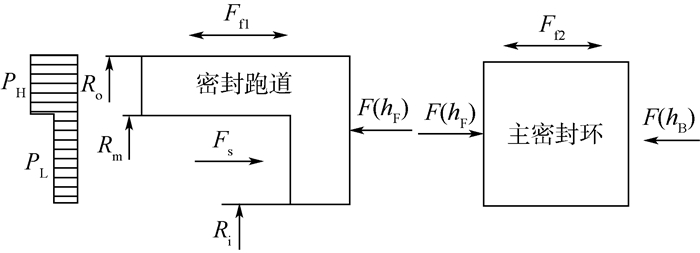 |
| Ro—密封跑道外径;Ri—密封跑道内径;Rm—密封跑道结构尺寸;F(hF)—前端面密封气膜力;F(hB)—后端面密封气膜力。 图 2 密封件受力图 Fig. 2 Force diagram of seal components |
| 图选项 |
其中:Ω为求解区域;R为气体常数;θ为角度。
2.2 端面气膜稳态压场 假设气膜内气体处于层流状态、忽略膜厚方向的速度变化和压力变化,由Navier-Stokes方程、连续性方程和气体状态方程推导得到计算动静压混合、单端面旋转的稳态广义雷诺方程的二维柱坐标无量纲表达形式:
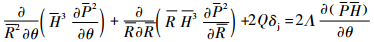 | (3) |
式中:R、H和P1分别为无量纲的密封环半径、膜厚以及压强;

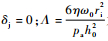
运用伽辽金方法建立变分方程,并令ξ=lnR,得到稳态雷诺方程的变分方程:
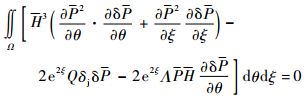 | (4) |
求解的边界条件如下:
1) 已知压力边界:p|r=ri=pi,p|r=ro=po。
2) 周期性边界:p(θ)=p(θ+2π/z),z为节流孔数量。
3) 节流孔边界:在连续性方程中增加了ρ,为节流孔单位面积流入的质量流量,将雷诺方程和节流孔流量方程联立求解得到节流孔出口压力。
2.3 稳态密封性能 1) 气膜反力:
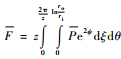
2) 气膜刚度:
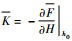
3) 泄漏量:泄漏量由前后端面节流孔质量流量QK1和QK2及前端面环形汇流质量流量QH三部分组成。
节流孔质量流量[15]:
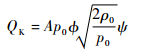 | (5) |
式中:
 |
其中:βk=[2/(k+1)]k/(k-1);pd为节流孔出口压力;?为流量系数;A为节流面积;k为气体常数;p0为供气压力;ρ0供气气体密度。
两圆盘间汇流的流量[16]为
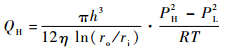 | (6) |
式中:前端面质量流量为Q1=QK1+QH,后端面质量流量为Q2=QK2,总质量流量为Qr=Q1+Q2。
3 密封系统动态求解 密封系统在工作过程中,外界干扰使主密封环和密封跑道偏离平衡位置。良好的密封系统设计,主密封环与密封跑道应具有一定的自适应性,从而避免由于密封端面直接碰撞导致密封端面磨损而造成泄漏量增加、甚至密封失效。
3.1 密封系统动力学方程 基于主密封环与密封跑道轴向受力分析,当瞬时扰动力FT在密封系统上作用t0后撤离,在0~t0内密封系统为受迫振动,当t>t0密封系统作自由振动。密封系统的动力学方程如下。
密封跑道:
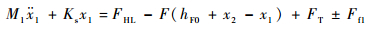 | (7) |
式中:M1为密封跑道质量。
主密封环:
 | (8) |
式中:M2为主密封环质量。
当t>t0,Fs=0,摩擦力的正负号取决于密封件运动方向,式中x1和x2分别表示密封跑道、主密封环偏离平衡位置位移。
当密封系统受到Fmcos (ωt) 的激振力 (ω为激振频率,Fm为激力振幅),密封系统作受迫振动,其动力学方程如下。
密封跑道:
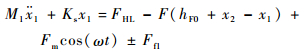 | (9) |
主密封环:
 | (10) |
引入Newmark-β法, 在时间t时,密封系统的加速度与速度可表示为
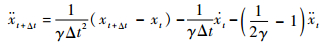 | (11) |
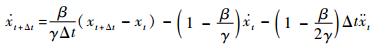 | (12) |
式中:下标t表示当前时刻,t+Δt为下一个时刻;β与γ可按照积分的精度和稳定性进行调整,当β≥0.5, γ≥0.25(0.5+β)2时,Newmark-β法是一种无条件稳定的格式。
3.2 端面气膜动态压场 在与式 (3) 同样的假设前提下推导得到无量纲瞬态雷诺方程:
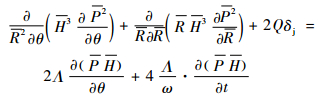 | (13) |
采用与式 (4) 相同方法,得到瞬态雷诺方程的变分方程。运用有限元法离散解域,并向后差分法离散时间项,得到离散瞬态雷诺方程:
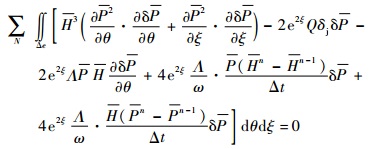 | (14) |
式 (14) 中各参数含义及边界条件与式 (4) 相同。节流孔的存在使其离散方程表现为二次超越非线性,采用分割因子结合Newton-Raphson线性化迭代方法求解。利用直接数值模拟法耦合求解式 (7)、式 (8) 和式 (14),得到密封系统自由振动的响应曲线,耦合求解式 (9)、式 (10) 以及式 (14) 得到密封系统受迫振动的动态响应。
4 计算结果及分析 4.1 结构参数 密封系统结构设计参数和工况条件如表 1所示,利用VC++根据上述算法编写分析软件,计算密封系统的稳态特性,计算结果如表 2所示。
表 1 气膜密封结构参数及工况参数 Table 1 Structure and operating parameters of gas film seal
| 参数 | 密封环外径Do/mm | 密封环内径Ds/mm | 节流孔直径Dk/mm | 节流孔数量z | 弹簧预紧力F/N | 进口压力PH/MPa | 出口压力PL/MPa | 旋转速度n/(r·min-1) |
| 数值 | 170 | 150 | 0.65 | 20 | 30 | 0.6 | 0.1 | 15 000 |
表选项
表 2 气膜密封稳态计算结果 Table 2 Calculation results of gas film seal in steady state
| 参数 | 前端面膜厚hF0/μm | 后端面膜厚hB0/μm | 前端面反力FF/N | 后端面反力FB/N | 前端面刚度KF/(107N·m-1) | 后端面刚度KB/(107N·m-1) | 泄漏量Qr/(kg·s-1) |
| 数值 | 17.27 | 22.93 | 1 480.8 | 1 483.3 | 3.16 | 4.96 | 0.009 4 |
表选项
4.2 动静压混合密封稳态密封性能 该密封系统端面为小孔浅腔动静压混合结构。当节流孔出口为环形均压腔时,为纯静压结构。图 3~图 5分别为动静压混合密封与纯静压密封的气膜支反力、刚度和泄漏量的计算结果。
 |
| 图 3 气膜支反力随膜厚的变化趋势 Fig. 3 Variation trend of gas film reaction force with film thickness |
| 图选项 |
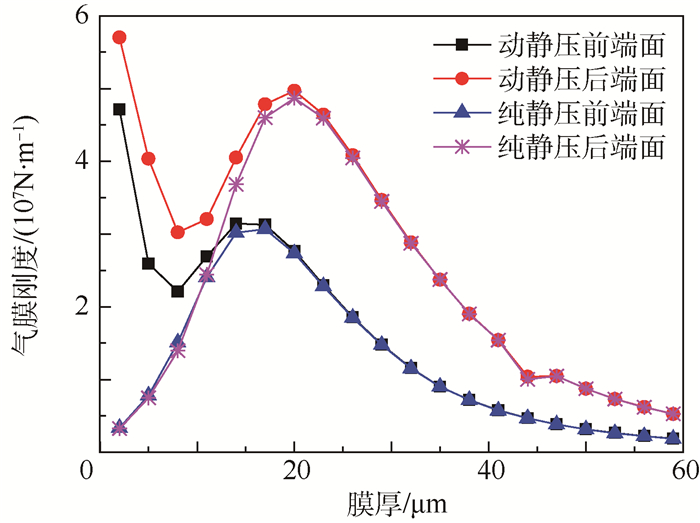 |
| 图 4 气膜刚度随膜厚的变化趋势 Fig. 4 Variation trend of gas film stiffness with film thickness |
| 图选项 |
 |
| 图 5 泄漏量随膜厚的变化趋势 Fig. 5 Variation trend of leakage with film thickness |
| 图选项 |
比较图 3中动静压混合密封和纯静压密封支反力,在膜厚较小时,动静压混合密封支反力明显高于纯静压支反力,动压效应明显,随着膜厚的增加,动压效应逐渐减弱,超过一定膜厚,与纯静压密封基本相同。
分析图 4可得,膜厚较小时,密封端面动压效应明显,其刚度变化趋势与动压密封趋势[17]相同;膜厚增加,动压效应减弱,气膜密封刚度曲线接近静压密封刚度曲线。单纯的动压密封工作膜厚薄,对端面加工精度要求高,当发生轴向窜动或角向摆动时易失效,而纯静压密封在膜厚较小时,刚度较小,对于增加系统稳定性不利。动静压混合密封结合了以上2种密封的优势,能在相对大的膜厚范围内保持较大刚度,有效提高了密封系统的稳定性。
从图 5可以看出,动静压混合密封泄漏量与纯静压密封基本相同,前端面泄漏量随膜厚增加呈非线性增加,后端面流量基本保持不变,主要是由于膜厚较大时,节流孔出口马赫数达到1成为临界状态,在这种情况下流量不变,发生阻塞流[18],流量不再增加,而随着膜厚的增加,前端面平板汇流流量仍不断增加,因此设计时为有效减少泄漏量,应使前端面膜厚保持在较小的范围内。
4.3 密封系统动态性能分析
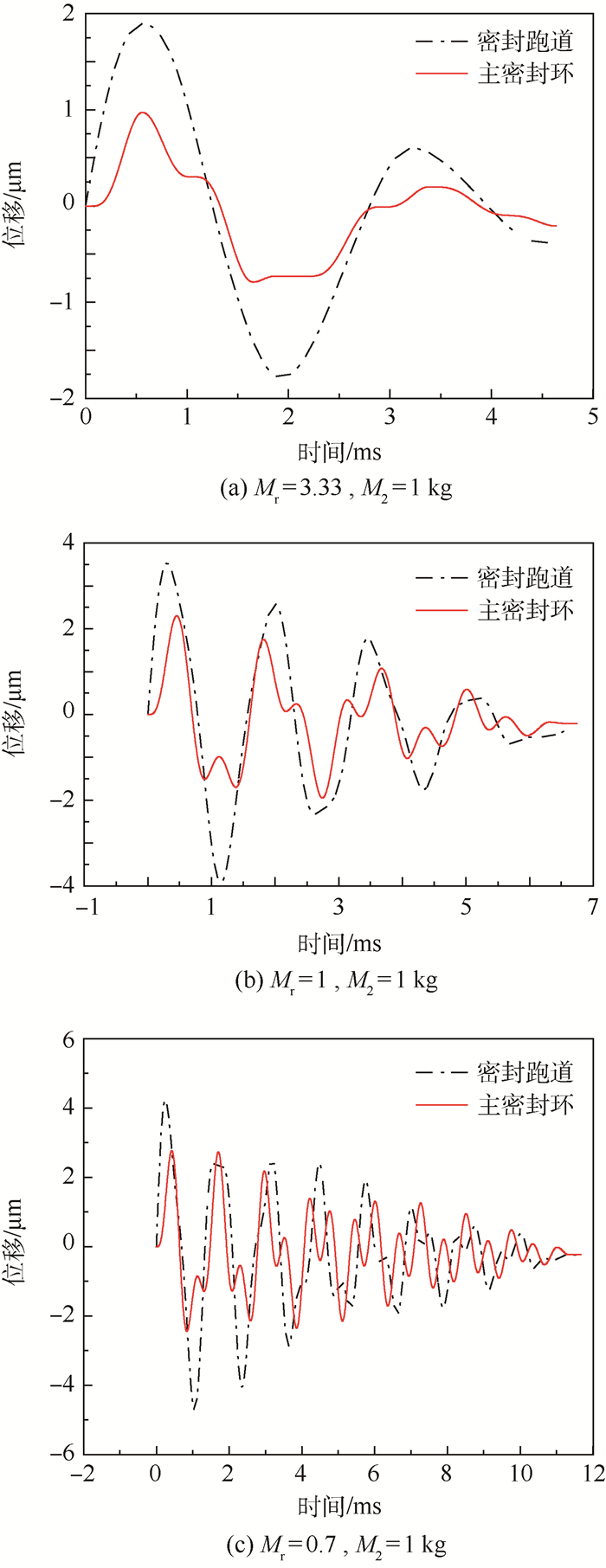
4.3.1 瞬时力扰动下密封系统的动态响应 图 6为在表 2工况条件下,密封跑道质量M1和主密封环质量M2在不同的质量比Mr下的系统自由振动响应曲线。
 |
| 图 6 不同质量比系统动态响应 Fig. 6 System dynamic response of different mass ratio |
| 图选项 |
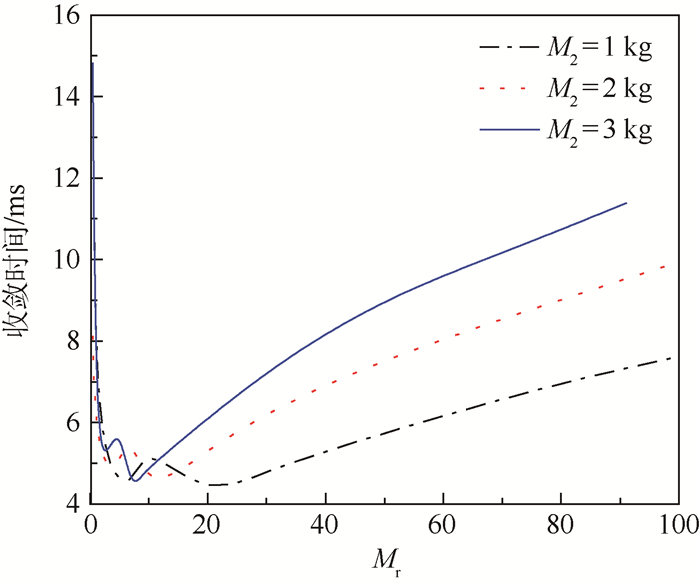
由图 6可知,由于气膜的阻尼、碳石墨环以及二次密封环阻尼的存在,密封跑道以及主密封环作振幅随时间而减小的减幅振动,密封系统逐渐恢复到稳定运行状态,不同的质量比系统的收敛时间不同;振动收敛时间与系统质量比的关系见图 7,由于气膜刚度及阻尼的非线性特征,随质量比增加,密封系统的收敛时间存在一个非线性段,在非线性段左端收敛时间随着质量比的增加而减少;在非线段的右端,随着质量比的增加,系统的收敛时间呈类线性增加,当主密封环与密封跑道的质量接近时,密封系统的收敛时间较短。
 |
| 图 7 振动收敛时间随质量比变化趋势 Fig. 7 Variation trend of vibration convergence time with mass ratio |
| 图选项 |
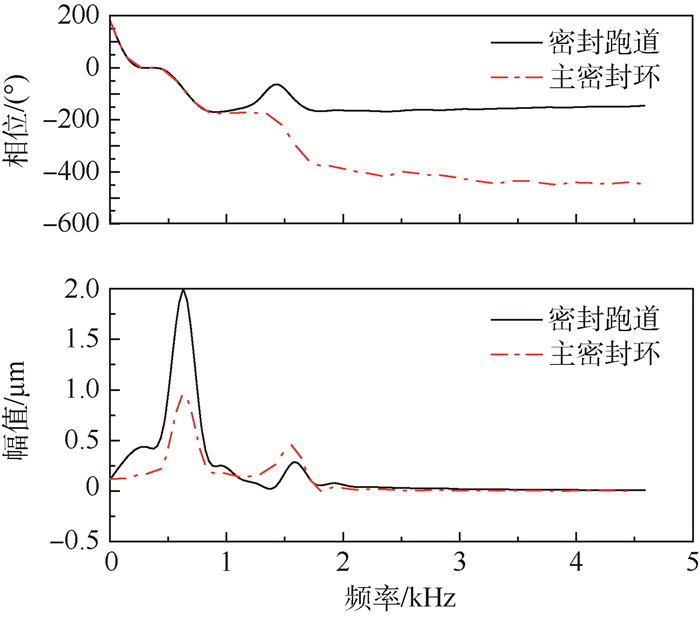
利用快速傅里叶变换 (FFT) 方法对响应信号进行频谱分析[19],提取动态响应中包含的主要频率成分,确定密封系统的固有振动频率。M1=1 kg, M2=1 kg时动态响应 (见图 6(b)) 的幅频曲线,如图 8所示。其第一阶固有频率f1=632.71 Hz,第二阶固有频率f2=1 581 Hz。
 |
| 图 8 系统响应频谱图 Fig. 8 Spectrum of system response |
| 图选项 |
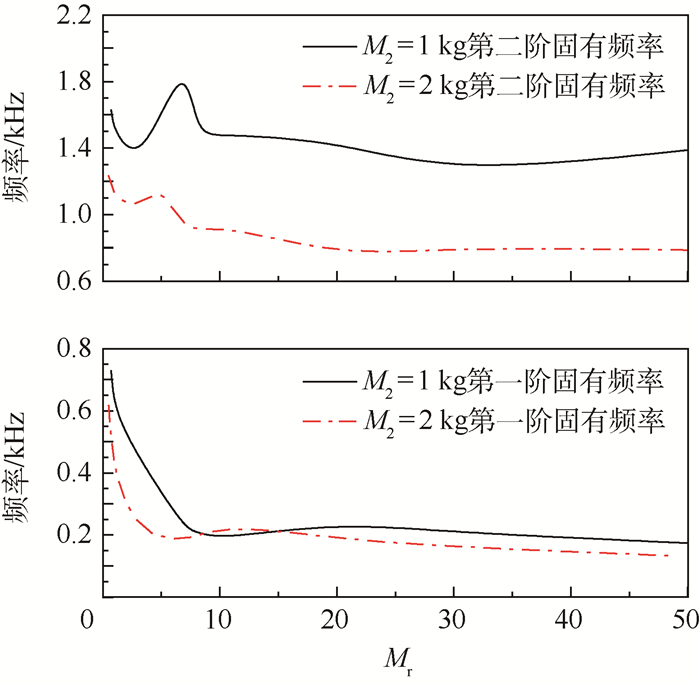
系统固有频率与质量比的关系如图 9所示,当质量比小于10时,固有频率随质量比的变化比较明显;当质量比大于10系统的固有频率变化比较平缓;设计结构要避开密封系统固有频率区间,以免发生共振。
 |
| 图 9 系统固有频率随质量比变化趋势 Fig. 9 Variation trend of natural frequency of system with mass ratio |
| 图选项 |
4.3.2 激振力扰动下密封系统的动态响应 对于具有二自由度振动特征的密封系统,当M1=1 kg,M2=1 kg时,根据频谱分析结果可得系统的第一阶固有频率和第二阶固有频率对应的角速度分别为ω1=3 973.42 rad/s和ω2=9 928.68 rad/s。图 10(a)为ω=1 000 rad/s时密封零件的振动曲线,其振动经过初始振荡后以激振频率振动,且振动幅度较小。图 10(b)和图 10(c)分别为激振频率为第一阶振动频率、第二阶振动频率时的振动响应,初始阶段振动幅度不断增加,由于阻尼的存在,经过一定时间,达到稳定振动的状态。但是其最大振幅达到了30 μm,振幅过大容易导致密封端面产生碰撞,从而造成密封系统不稳定、泄漏量增加。由于发动机转子转动可产生频率固定的激振力,因此设计时要考虑密封系统的两阶共振频率与发动机转速之间的关系,避开密封系统的共振频带。
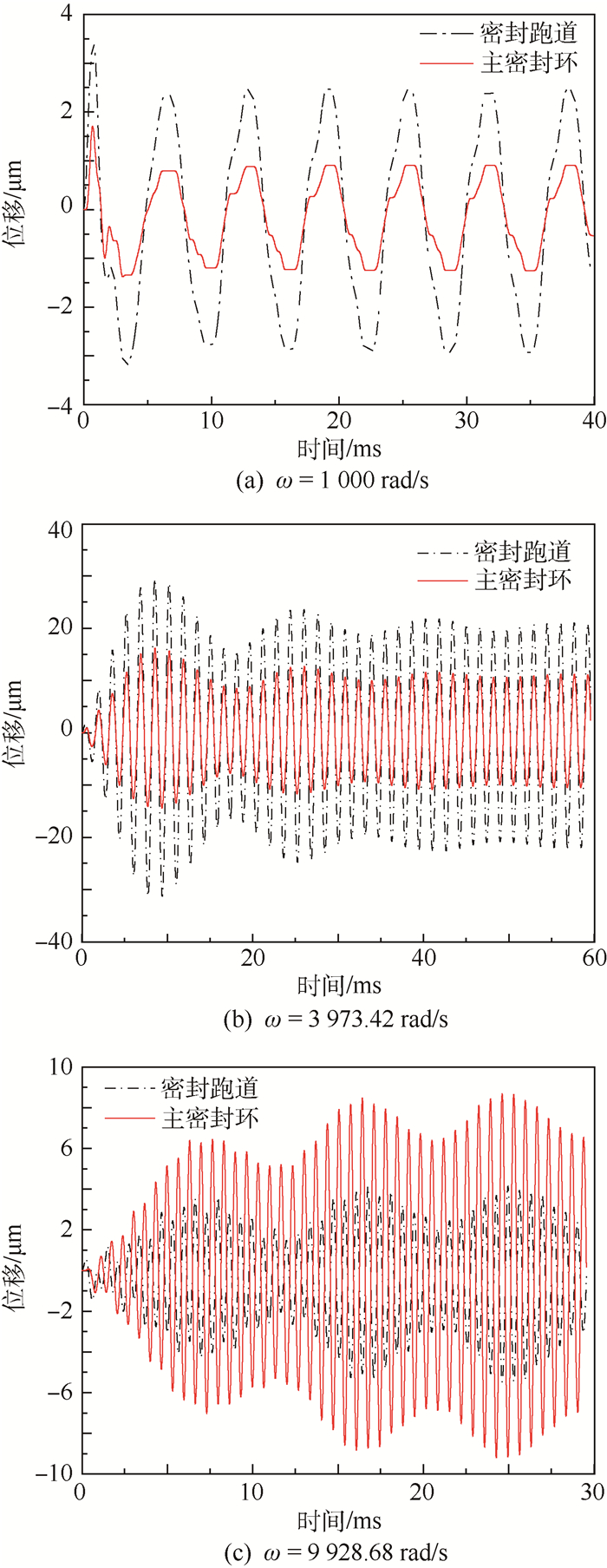 |
| 图 10 不同激振频率密封系统动态响应曲线 Fig. 10 Seal system dynamic response curves of different excitation frequency |
| 图选项 |
5 结论 1) 所述动静压混合气膜密封结构能在较大膜厚范围内保持较高的气膜刚度,气膜的工作范围增加允许系统更大的轴向跳动,且密封系统仍保持良好的稳定性。
2) 双端面气膜密封系统具有二自由度振动系统特征,在相同扰动下,振动收敛时间分布存在非线性区域、类线性增加区域以及类线性减少区域,且主密封环与密封跑道质量差距越大,其收敛时间越长。
3) 分析自由振动信号的频域,系统具有两阶固有频率,当激振频率位于系统固有频率附近时,密封系统振幅显著增加,可能导致系统失稳,在共振频率之外,振幅较小,密封系统稳定性较好。
参考文献
| [1] | GANBLE W L.Counter-rotating intershaft seals for advanced engines:AIAA-1984-1216[R].Reson:AIAA, 1984. |
| [2] | 吴宁兴, 赵宗坚. 反转轴间气膜密封可行性试验研究[J].航空发动机, 2001(4): 20–25.WU N X, ZHAO Z J. Experimental study on the feasibility of gas film seal between the counter shaft[J].Journal of Aerospace Power, 2001(4): 20–25.(in Chinese) |
| [3] | 王之栎, 郭艳丽. 反转轴间气膜密封的结构参数与密封性能分析[J].润滑与密封, 2008, 33(1): 68–72.WANG Z L, GUO Y L. Anti-air film between the shaft seal structure parameters and sealing performance analysis[J].Lubrication Engineering, 2008, 33(1): 68–72.(in Chinese) |
| [4] | 王之栎, 刘国西. 反转轴间气膜密封动特性分析[J].北京航空航天大学学报, 2010, 36(5): 509–512.WANG Z L, LIU G X. Gas seal dynamic analysis between the counter shaft[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(5): 509–512.(in Chinese) |
| [5] | GABRIEL R P. Fundamentals of spiral groove non-contacting face seals[J].Lubrication, 1994, 50(3): 215–224. |
| [6] | LEE S C, ZHENG X L. Analyses of both steady behavior and dynamic tracking of non-contacting spiral-grooved gas face seals[J].Computers & Fluids, 2013, 88(12): 326–333. |
| [7] | MILLER B A, GREEN I. Numerical formulation for the dynamic analysis of spiral-grooved gas face seals[J].Journal of Tribology, 2001, 123(2): 395–403.DOI:10.1115/1.1308015 |
| [8] | ZHANG H J, LANDERS R G, MILLER B A, et al. Adaptive control of mechanical gas face seals with rotor runout and static stator misalignment[J].Journal of Dynamic Systems, Measurement, and Control, 2010, 132(4): 558–564. |
| [9] | 丁雪兴, 张海舟. 螺旋槽干气密封气膜振动测试与稳定性分析[J].振动、测试与诊断, 2013, 33(2): 231–235.DING X X, ZHANG H Z. Spiral groove dry gas seal gas membrane vibration testing and stability analysis[J].Journal of Vibration, Measurement & Diagnosis, 2013, 33(2): 231–235.(in Chinese) |
| [10] | JAHN I H J, ROWNTREE G M.Intershaft seal:US2012/0043725 A1[P].2012-02-23. |
| [11] | JAHN I H J, DAVIES C.Intershaft seal:US2014/0049010 A1[P].2014-02-20. |
| [12] | 李树森, 刘暾. 精密离心机静压气体轴承主轴系统的动力学特性分析[J].机械工程学报, 2005, 41(2): 28–32.LI S S, LIU T. Dynamics of precision centrifuge hydrostatic gas bearing spindle system analysis[J].Journal of Mechanical Engineering, 2005, 41(2): 28–32.DOI:10.3901/JME.2005.02.028(in Chinese) |
| [13] | 魏斌, 郝木明, 陈亮. 非接触式气体端面密封的动力学分析方法概述[J].内蒙古石油化工, 2006, 32(5): 182–184.WEI B, HAO M M, CHEN L. Kinetic analysis of non-contact gas seal overview[J].Inner Mongolia Petrochemical Industry, 2006, 32(5): 182–184.(in Chinese) |
| [14] | 卢宁. 螺旋槽气体端面密封动态特性分析[J].内蒙古石油化工, 2008, 34(6): 81–83.LU N. Spiral groove gas face seals dynamic performance analysis[J].Inner Mongolia Petrochemical Industry, 2008, 34(6): 81–83.(in Chinese) |
| [15] | 刘暾, 刘育华, 陈世杰. 静压气体润滑[M].哈尔滨: 哈尔滨工业大学出版社, 1990: 100-130.LIU T, LIU Y H, CHEN S J. Static pressure gas lubrication[M].Haerbin: Harbin Institute of Technology Press, 1990: 100-130.(in Chinese) |
| [16] | 王云飞. 气体润滑理论与气体轴承设计[M].北京: 机械工业出版社, 1990: 20-50.WANG Y F. Gas gas bearing design and lubrication theory[M].Beijing: China Machine Press, 1990: 20-50.(in Chinese) |
| [17] | 刘雨川, 徐万孚. 端面气膜密封的高性能端面结构[J].航空学报, 2000, 21(2): 187–190.LIU Y C, XU W F. High-performance end structures gas film face seal[J].Acta Aeronautica et Astronautica Sinica, 2000, 21(2): 187–190.(in Chinese) |
| [18] | 江宏俊. 流体力学 (下册)[M].北京: 高等教育出版社, 1985: 50-65.JIANG H J. Fluid dynamics (Volume Ⅱ)[M].Beijing: Higher Education Press, 1985: 50-65.(in Chinese) |
| [19] | 金连文, 韦岗. 现代数字信号处理简明教程[M].北京: 清华大学出版社, 2003: 19-29.JIN L W, WEI G. Modern digital signal processing simple tutorial[M].Beijing: Tsinghua University Press, 2003: 19-29.(in Chinese) |
