经验模态分解(Empirical Mode Decomposition,EMD)[11-12]是一种新型的时频分析方法,能够将信号分解为若干固有模态函数(Intrinsic Mode Function,IMF),具有自适应性、正交性及完备性的特点,已广泛应用于能源、化工、医疗、气象等领域。樊辰阳等[13]采用EMD方法对信号中混杂的干扰噪声进行滤除,提取出真实的涡街成分,通过对在线涡街流量信号进行仿真分析,验证了该方法的有效性。Sun和Zhang[12]结合EMD方法对涡街流量计中原始信号分解的结果,提取各固有模态函数的能量比,分析流动中的扰动对涡街流量计测量性能的影响。Mao等[14]基于EMD方法,通过建立模型,经4步即可模拟非平稳车辆随机信号。Sun等[15]基于EMD方法分解气液两相流复杂信号,识别文丘里管内气液两相流的流型,并通过气水和气油两相流的实验验证了该方法在单相流、泡状流、弹状流和塞状流的准确性。然而,EMD方法也存在模态混淆[16]的缺陷,这削弱了信号的分解效果,影响了EMD方法的使用。为此,文献[16-19]中提出一种改进的EMD方法,即集总经验模态分解(Ensemble Empirical Mode Decomposition,EEMD),通过在待分解信号中加入噪声信号,用以改善EMD方法的模态混淆等不足之处。
EEMD方法通常与Hilbert变换结合使用,Hilbert变换的目的是获得信号的瞬时频率特征。与小波变换、Wigner-Ville分布等方法相比,该变换得到的瞬时频率能够更好的表征信号在局部时间点上特征。张艳霞等[20]利用Hilbert变换得到了实信号幅值函数的特点,提出串联补偿线路故障点位置的识别判据,形成了适用于串联补偿线路的距离保护方案。曾伟等[21]基于Hilbert变换,提出一种新的激光超声波传播图像方法,有效地提取超声波信号在缺陷处传播的信息。范锋等[22]提出一种基于Hilbert变换重建相位的理论和方法,提高了数字全息相位重建精度。
本文通过实验获得不同空气流量下表征涡街流量计尾迹振荡的管壁差压信号,采用EEMD-Hilbert谱方法对该差压信号进行分析,以深入提取和揭示涡街流量计尾迹振荡特性。首先,利用EEMD方法对涡街流量计管壁差压信号进行分解,得到IMF分量,再对IMF分量进行Hilbert变换,观察EEMD-Hilbert方法的去噪效果,进而研究涡街流量计尾迹振荡信号的特征。
1 EEMD-Hilbert谱计算方法 EEMD-Hilbert谱的计算流程如图 1所示。
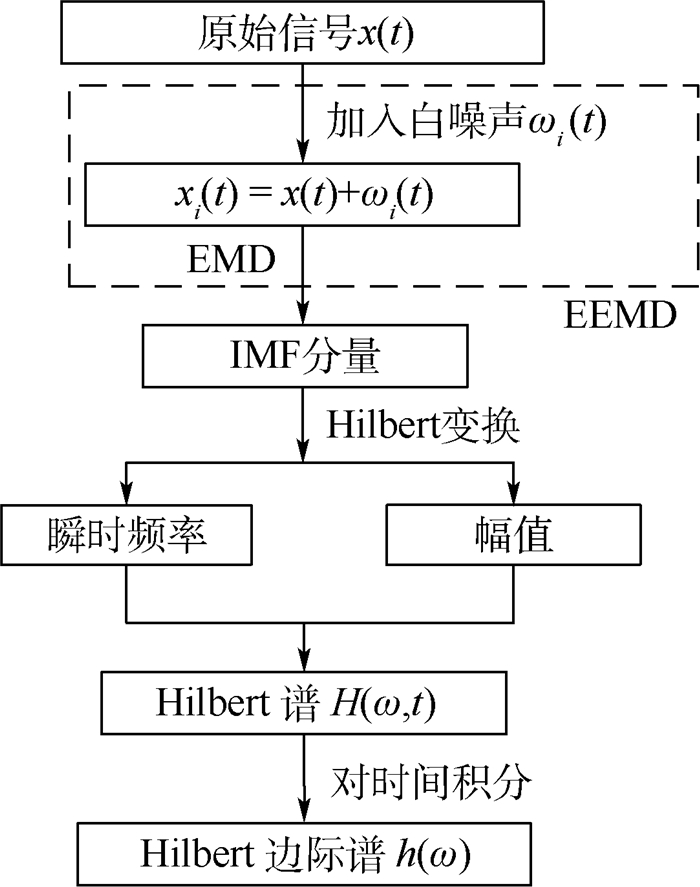 |
| 图 1 EEMD-Hilbert谱的计算流程 Fig. 1 Calculation procedure of EEMD-Hilbert spectrum |
| 图选项 |
EEMD是一种改进的EMD方法,通过在待分解的原始信号中加入白噪声,可将非平稳非线性信号分解成一组稳态线性的序列集。这些序列称为IMF分量,必须满足:在整个数据段内,数据的极值点和过零点的个数必须相等或相差最多不能超过一个;在任意时刻,由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为零,即上、下包络线相对于时间轴局部对称。IMF反映了原始信号的动态特性。
利用EEMD对信号进行处理时,主要分为以下步骤:
步骤1?向原始信号x(t) 加入正态分布的白噪声ωi(t),即
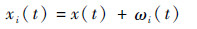 | (1) |
步骤2?利用EMD将加噪信号xi(t) 分解成IMF。
步骤3?重复步骤1和步骤2,每次加入新的白噪声序列。
步骤4?将每次得到的IMF集成均值作为最终结果,即
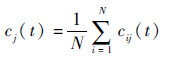 | (2) |
式中:cj(t) 为原始信号x(t) 经EEMD分解得到的第j个IMF;cij(t) 为第i次加入噪声后分解产生的IMF分量;N为加入白噪声的次数。
然后,分别对各IMF进行Hilbert变换
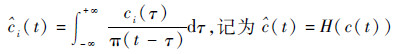 | (3) |
构造解析信号
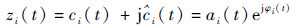 | (4) |
得到幅值函数和相位函数
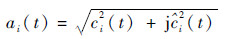 | (5) |
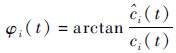 | (6) |
求得瞬时频率
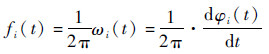 | (7) |
进而得到x(t) 的另一种表示方式
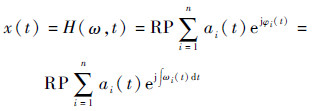 | (8) |
式中:残差rn被省略,RP表示取实部。式(8) 即为原始信号x(t) 的Hilbert谱。则Hilbert边际谱定义为
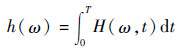 | (9) |
式中:T为信号的采样时间。H(ω, t) 描述了信号幅值在整个频率段上随时间和频率的分布状况,而h(ω) 仅能反映信号幅值在整个频率段上随频率的变化情况。与Fourier谱相比,Hilbert边际谱摆脱了传统Fourier变换的局限,且不能发生能量泄露,能够准确地描述各频率成分的幅值,具有很高的分辨率。
2 实验装置与过程 实验系统主要由钟罩式气体流量标准装置、流量显示装置、实验段和球阀组成,如图 2所示。钟罩式气体流量标准装置用于给出实验的标准体积流量值,其准确度为0.5级,工作压力为5 kPa,标准容积为2 000 L,流量范围为0~220 m3/h。实验在环境温度为20 ℃时进行,通过球阀来调节空气流量,通过流量显示装置读出进入实验段的空气的标准流量值。采用管壁差压法进行测量。
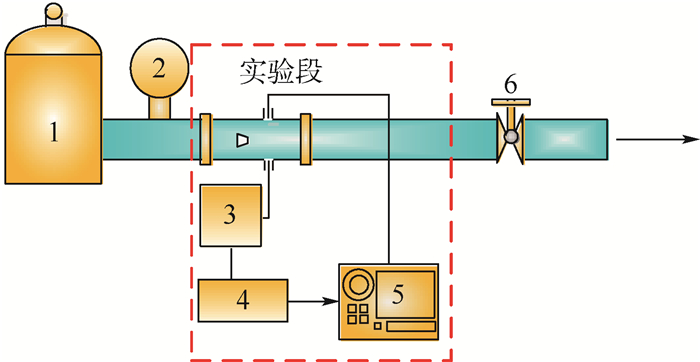 |
| 图 2 实验系统组成 Fig. 2 Experimental system composition |
| 图选项 |
实验段由涡街流量计、差压传感器、信号调理板和数字示波器组成。涡街流量计的测量管径为50 mm,流量系数已知,准确度为1级,梯形旋涡发生体的迎流面宽度为14 mm,在旋涡发生体两侧开有一对取压孔连接差压传感器。实验中,当空气流过涡街流量计时,由于旋涡发生体的存在,管内的空气发生扰动,其尾迹振荡诱发下游流体压力发生变化,差压信号经差压传感器检测、信号调理板进行放大,最终由数字示波器进行记录采样。实验中采用Honeywell公司26PC系列差压传感器作为检测元件,采用Tektronix TDS 430A双通道数字示波器来记录和存储数据。示波器的采样频率为2 500 Hz,每次采样5 000个数据点。采样5 000点能够使得采样结果较好地保留了信号的原有特征,且保证较高的频率分辨率。
3 结果与讨论 3.1 IMF分量 本文以管壁差压信号作为涡街流量计输出的原始信号,对于不同流量Q下涡街流量计的管壁差压信号进行EEMD分解,得到各IMF分量,如图 3所示。x(t) 为原始信号,c1~c6为各原始信号经分解后得到的主要IMF分量,分别表示瞬时频率从大到小的不同频率成分。
 |
| 图 3 EEMD分解结果 Fig. 3 Decomposition results of EEMD |
| 图选项 |
通过观察各IMF分量的波动形式来判断IMF分量是否为涡街成分,将波动具有周期性、波形十分接近正弦波的IMF分量作为涡街成分。观察图 3可知,图 3(a)中c2、图 3(b)中c3、图 3(c)中c2、图 3(d)中c1分量均对应于实际涡街成分,具有规则稳定的波动(波动具有周期性,接近正弦波);而其他分量反映了叠加在涡街成分上的各种噪声。由于c6之后的IMF分量及残差的幅度和频率较小,对后续讨论影响较小,因而图中未给出。
3.2 Hilbert谱分析 按照图 1所示流程,对4种典型流量下的原始信号进行EEMD分解、Hilbert变换后,得到Hilbert谱[23-24],如图 4所示。
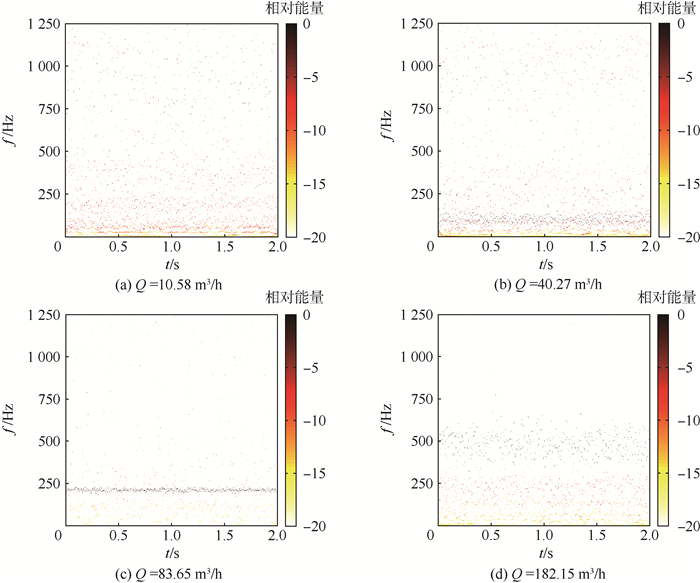 |
| 图 4 不同流量下尾迹的Hilbert谱 Fig. 4 Hilbert spectra of wake at different flow rates |
| 图选项 |
Hilbert谱将IMF的振幅以颜色深浅的形式表现在频率-时间-能量图上,描述了各分量的幅值在整个频率段上随时间和频率的变化规律,图中点的颜色越深,振幅越大,颜色的深浅也反映了能量的相对大小。
如图 4所示,图 4(a)的29 Hz附近,图 4(b)的95 Hz附近,图 4(c)的214 Hz附近,图 4(d)的480 Hz附近,能量较高且集中,其他区域能量较低且杂乱无章地分布。由于涡街流量计的输出信号中涡街成分的能量较大,且频率不变,噪声信号能量较小,因而推断该4处频率附近的信号为涡街成分,其余分散的信号为噪声信号。
对比图 4(a)~图 4(d)可见,随着流量的增大,Hilbert谱中点的颜色越深,这表明能量逐渐增大,且高频区域噪声信号逐渐减弱。信号的能量由分散分布转变为集中分布到一个较窄的频带,进而分散为2个频带,这是由引压管的固有频率引起。
当空气流量较小时,频率较小,涡街成分较弱,能量较小,因而在Hilbert谱中用较浅的点来表示。涡街成分几乎淹没在噪声中,噪声能量也较小,且杂乱无章地分布于Hilbert谱的整个频带,故涡街成分的频率在Hilbert谱中分布不明显。
将Hilbert边际谱在时间上进行积分,得到Hilbert边际谱。Hilbert边际谱能反映信号幅值在整个频率段上随频率的变化情况。能量在某个频率上存在最大值反映了信号的主要成分为该频率成分。
计算过程中,Hilbert边际谱及主峰频率主要受到信号组成成分、终止准则和白噪声幅值大小的影响。
3.3 线性分析 为研究EEMD-Hilbert谱方法下得到的尾迹波动的流量与旋涡脱落频率的线性程度,以空气流量为10.58~182.15 m3/h的涡街流量计管壁差压信号为研究对象,EEMD-Hilbert谱方法进行研究,并以Fourier变换作为对照,其中,Fourier变换通过快速Fourier变换(FFT) 算法来实现。经上述2种方法处理后,分别得到Fourier谱和Hilbert边际谱,根据频谱的主峰频率可得到涡街频率。涡街流量计仪表系数K标定为9 244.73 m-3,由式(10) 计算得到的理论涡街频率。
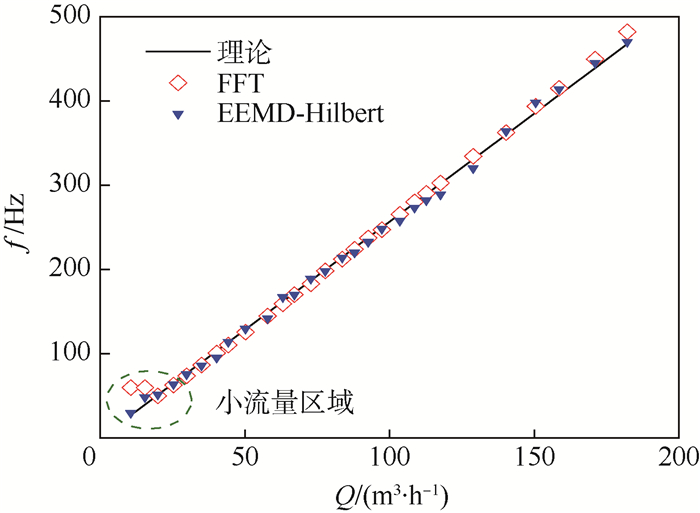
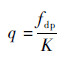 | (10) |
式中:q为介质流量;fdp为管壁差压频率。
图 5给出了利用FFT、EEMD-Hilbert谱方法得到的空气流量值与涡街频率之间的关系,由图可见,在整个流量范围10.58~182.15 m3/h内,2种方法的处理精度不同。当空气流量为30~190 m3/h时,FFT、EEMD-Hilbert处理得到的涡街频率与涡街的理论频率值吻合较好,且涡街频率值与流量成良好的线性关系。
 |
| 图 5 尾迹波动的流量与涡街频率的关系 Fig. 5 Wake fluctuation flow rates versus frequencies |
| 图选项 |
当空气流量为10~30m3/h时,FFT变换所得涡街频率误差较大,即空气流量分别为10.58 m3/h和15.47 m3/h时,FFT方法的误差分别为120%和50%,而EEMD-Hilbert方法误差仅为9%和20%,由此可见,EEMD-Hilbert变换对于涡街频率的检测具有更高的精度。这是由于管壁差压信号为非线性、非稳定信号,在小流量情况下,涡街成分较弱,几乎淹没在噪声信号里,FFT变换基于信号的线性和稳定性假设[25],在分析非线性、非稳定信号时,不可避免地截止长周期(即小频率) 谐波分量,导致部分小频率涡街成分被截止,破坏了涡街成分,此时FFT方法主要分析的成分为噪声信号,因而所求频率并非是涡街成分的频率;而EEMD-Hilbert方法是在时间域内进行滤波,能将涡街成分与噪声信号较好地分离。原始信号经EEMD分解后,所得各IMF分量较好地保留信号的物理特征,因而保留了涡街成分地固有特征,即数据物理空间内的线性和非稳定性特征。
EEMD-Hilbert方法的误差主要来源于仪器设备的噪声,包括管道振动、湍流脉动产生的噪声,引压管的规则振动产生的噪声,以及工业现场其他设备的干扰等。对于小流量情况下,这些噪声对于涡街频率的准确识别有很大的干扰性,因而降低了频率提取的精度。
此外,本文中,对于FFT方法,流量越小,误差越大,而EEMD-Hilbert方法尚无此趋势。通过控制钟罩式气体流量标准装置的调节阀,可拓展测量下限,观察测量误差是否随着流量减小而增大。
3.4 能量比分析 信噪比[26]为信号的能量与噪声能量之比,根据该定义,研究不同流量下原始信号经Fourier变换及EEMD-Hilbert方法处理后的信噪比情况。使用边际谱中峰值点及前后两点幅度之和Amm来表征涡街成分的能量,用边际谱中涡街成分以外的噪声幅度之和(Asu-Amm,Asu为所有点的幅值和) 来表征噪声的能量,因而能量比Ar为信噪比的一种反映。能量比Ar越大则信噪比越大。
利用各边际谱峰值点的幅度,定义峰值点及前后两点的幅度之和为
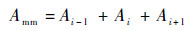 | (11) |
式中:i为峰值点。
按照此定义,求出谱中所有点的幅度总和Asu,得到能量比Ar:
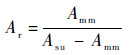 | (12) |
图 6为尾迹波动的流量与能量比的关系,由图可见,随着空气流量的增大,FFT方法及EEMD-Hilbert谱方法所得能量比均先增大至最大值,再减小。同一空气流量下,能量比大小关系为:Ar (EEMD-Hilbert)>Ar (FFT),且在最大值点,EEMD-Hilbert谱方法得到的能量比为0.78,远大于FFT方法达到的能量比0.08。这说明EEMD-Hilbert谱方法能够有效地分离涡街成分和噪声信号,提高信号的信噪比。同时,也从侧面揭示了该方法能够提高频率提取精度的原因。
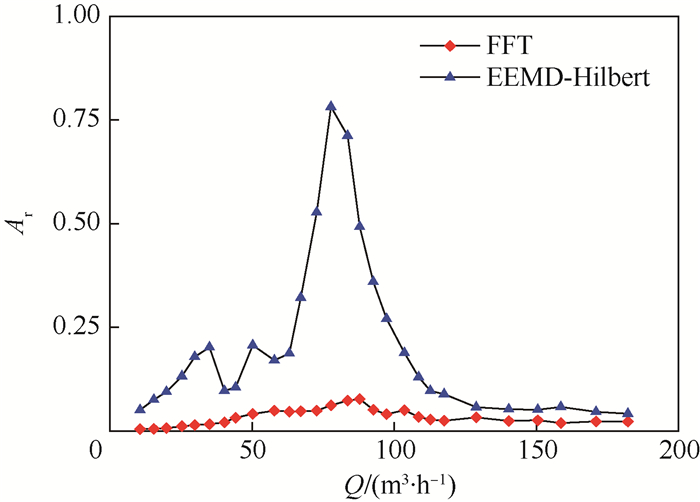 |
| 图 6 尾迹波动的流量与能量比的关系 Fig. 6 Wake fluctuation flow rates versus energy ratio |
| 图选项 |
在不同流量条件下能量比的差异性较大,这主要受到引压管固有频率的影响,能量比先增大是由于空气流量不断增大,涡街成分的能量不断加强,且涡街成分的频率在不断地接近引压管的固有频率,两者能量不断相互叠加,故信噪比增大。能量比在涡街频率与引压管固有频率相同时达到最大值。随后,涡街频率逐渐远离引压管固有频率,能量不再叠加,能量比减小,且随着流量的增大,空气流速增大,导致由管道振动引起的噪声信号逐渐增强,故信噪比降低。因而,在实际测量中,需谨慎选取引压管的型号。
4 结论 本文采用管壁差压法,在不同流量下利用涡街流量计、差压传感器等实验设备测量了空气流过梯形旋涡发生体的两侧差压,基于EEMD-Hilbert谱方法,提取旋涡脱落的频率,进而获得Hilbert谱及Hilbert边际谱、能量比,并与经典FFT方法进行对比。得到以下结论:
1) EEMD-Hilbert谱方法能够有效分解涡街流量计噪声信号,且分解过程几乎无模态混叠现象发生,不会破坏信号的固有成分。
2) EEMD-Hilbert谱方法对小流量下涡街频率的识别精度较高,比FFT方法精度高30%以上,该优势可用于扩展涡街流量计的测量下限,拓宽工业中涡街流量计的适用范围。
3) Hilbert谱图直观给出了频率-时间-能量的三维关系,揭示了涡街成分及其噪声的频率、能量随时间的瞬时分布。
参考文献
| [1] | LI Z, SUN Z Q. Development of the vortex mass flowmeter with wall pressure measurement[J].Measurement Science Review, 2013, 13(1): 20–24. |
| [2] | SUN Z Q. Design and performance of the converging-diverging vortex flowmeter[J].Metrology and Measurement Systems, 2011, 18(1): 129–136. |
| [3] | PENG B H, MIAU J J, BAO F, et al. Performance of vortex shedding from a circular cylinder with a slit normal to the stream[J].Flow Measurement and Instrumentation, 2012, 25(3): 54–62. |
| [4] | 陈洁, 刁品高. 涡街流量计信号处理方法研究与系统设计[J].中国测试, 2015, 41(2): 105–109.CHEN J, DIAO P G. Signal processing method study and system design for vortex flowmeter[J].China Measurement and Test, 2015, 41(2): 105–109.(in Chinese) |
| [5] | 宋佳忆, 李斌, 樊辰阳. 基于双通道的涡街流量计信号处理系统研究[J].工业控制计算机, 2015, 28(6): 108–109.SONG J Y, LI B, FAN C Y. Research on signal processing system of vortex flowmeter based on dual-channel[J].Industrial Control Computer, 2015, 28(6): 108–109.(in Chinese) |
| [6] | 贾德利, 于泳, 陈召, 等. 分层注水工艺中涡街流量计信号处理方法研究[J].传感技术学报, 2015(10): 1513–1519.JIA D L, YU Y, CHEN Z, et al. Research on processing methods of vortex flowmeter signal processing in layered water injection technology[J].Chinese Journal of Sensors and Actuators, 2015(10): 1513–1519.(in Chinese) |
| [7] | 于希宁, 袁素梅, 田亮, 等. 基于递推DFT算法的涡街流量计信号处理系统[J].中国仪器仪表, 2009(3): 76–79.YU X N, YUAN S M, TIAN L, et al. The signal processing system of vortex flowmeter based on recursive DFT algorithm[J].China Instrumentation, 2009(3): 76–79.(in Chinese) |
| [8] | SUN Z Q, SHAO S, GONG H. Gas-liquid flow pattern recognition based on wavelet packet energy entropy of vortex-induced pressure fluctuation[J].Measurement Science Review, 2013, 13(2): 83–88. |
| [9] | 刘红梅, 王少萍, 欧阳平超. 基于小波包和Elman神经网络的液压泵故障诊断[J].北京航空航天大学学报, 2007, 33(1): 67–71.LIU H M, WANG S P, OUYANG P C. Fault diagnosis based on wavelet package and Elman neural network for a hydraulic pump[J].Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(1): 67–71.(in Chinese) |
| [10] | 田琳, 陈颖频, 梁华兰. 平滑伪Wigner-Ville分布在地震信号处理中的应用[J].新疆师范大学学报(自然科学版), 2013, 32(3): 1–4.TIAN L, CHEN Y P, LIANG H L. The application of smoothing pseudo Wigner-Ville distribution in seismic signal processing[J].Journal of Xinjiang Normal University (Natural Sciences Edition), 2013, 32(3): 1–4.(in Chinese) |
| [11] | SUN Z Q, ZHOU J M, ZHOU P. Application of Hilbert-Huang transform to denoising in vortex flowmeter[J].Journal of Central South University of Technology, 2006, 13(5): 501–505.DOI:10.1007/s11771-006-0076-7 |
| [12] | SUN Z Q, ZHANG H J. Application of empirical mode decomposition based energy ratio to vortex flowmeter state diagnosis[J].Journal of Central South University of Technology, 2009, 16(1): 154–159.DOI:10.1007/s11771-009-0026-2 |
| [13] | 樊辰阳, 陈洁, 刘晓佳, 等. 基于EMD的幅值归一化涡街流量计信号处理[J].工业控制计算机, 2015, 28(3): 125–126.FAN C Y, CHEN J, LIU X J, et al. De-noising method of vortex signal with normalized amplitude based on EMD[J].Industrial Control Computer, 2015, 28(3): 125–126.(in Chinese) |
| [14] | MAO C, JIANG Y, WANG D, et al. Modeling and simulation of non-stationary vehicle vibration signals based on Hilbert spectrum[J].Mechanical Systems and Signal Processing, 2015, 50-51: 56–69.DOI:10.1016/j.ymssp.2014.05.005 |
| [15] | SUN B, ZHANG H, CHENG L, et al. Flow regime identification of gas-liquid two-phase flow based on HHT[J].Chinese Journal of Chemical Engineering, 2006, 14(1): 24–30.DOI:10.1016/S1004-9541(06)60033-5 |
| [16] | WU Z, HUANG N E. Ensemble empirical mode decomposition:A noise assisted data analysis method[J].Advances in Adaptive Data Analysis, 2009, 1(1): 1–41.DOI:10.1142/S1793536909000047 |
| [17] | LI X, CHEN W, ZHOU Y. A robust method for analyzing the instantaneous attributes of seismic data:The instantaneous frequency estimation based on ensemble empirical mode decomposition[J].Journal of Applied Geophysics, 2014, 111: 102–109.DOI:10.1016/j.jappgeo.2014.09.017 |
| [18] | WU Z, HUANG N E, CHEN X. The multi-dimensional ensemble empirical mode decomposition method[J].Advances in Adaptive Data Analysis, 2009, 1(3): 339–372.DOI:10.1142/S1793536909000187 |
| [19] | 李银勇, 行鸿彦, 易秀成. 基于EEMD分解的电场时序差分在雷电预警中的可行性分析[J].科学技术与工程, 2015, 15(29): 15–20.LI Y Y, XING H Y, YI X C. Feasibility analysis on electric field second order difference based on EEMD decomposition in thunderstorm warning[J].Science Technology and Engineering, 2015, 15(29): 15–20.(in Chinese) |
| [20] | 张艳霞, 宣文博, 田斌宾, 等. 基于Hilbert变换的串联电容补偿线路距离保护[J].电力系统自动化, 2014, 38(7): 77–82.ZHANG Y X, XUAN W B, TIAN B B, et al. Distance protection for series capacitor compensated lines based on Hilbert transform[J].Automation of Electric Power Systems, 2014, 38(7): 77–82.(in Chinese) |
| [21] | 曾伟, 王海涛, 田贵云, 等. 基于Hilbert变换的激光超声波成像技术在缺陷检测中的应用[J].中国激光, 2014, 41(5): 188–194.ZENG W, WANG H T, TIAN G Y, et al. Application laser ultrasound imageing technology for detectingdefect based on Hilbert transform[J].Chinese Journal of Lasers, 2014, 41(5): 188–194.(in Chinese) |
| [22] | 范锋, 栗军香, 宋修法, 等. 基于Hilbert变换实现数字全息高精度相位重建[J].物理学报, 2014, 63(19): 140–147.FAN F, LI J X, SONG X F, et al. High accuracy phase reconstruction of digital hologram by Hilbert transform[J].Acta Physica Sinica, 2014, 63(19): 140–147.(in Chinese) |
| [23] | HUANG N E, CHEN X, LO M, et al. On Hilbert spectral representation:A true time-frequency representation for nonlinear and nonstationary data[J].Advances in Adaptive Data Analysis, 2011, 3(1): 63–93. |
| [24] | HUANG N E, CHEN X, LO M, et al. A review on Hilbert-Huang transform:Method and its applications to geophysical studies[J].Reviews of Geophysics, 2008, 46(2): 3043–3061. |
| [25] | HUANG N E, WU Z, ON J E P, et al. Reductions of noise and uncertainty in annual global surface temperature anomaly data[J].Advances in Adaptive Data Analysis, 2009, 1(3): 447–460.DOI:10.1142/S1793536909000151 |
| [26] | PENG J, WANG W, FANG M. Hilbert-Huang transform (HHT) based analysis of signal characteristics of vortex flowmeter in oscillatory flow[J].Flow Measurement and Instrumentation, 2012, 26(4): 37–45. |
