车间调度是生产加工的重要环节，基本任务之一是合理安排各机器上的待加工工件的顺序，使得最大完工时间最短。作为流水车间调度问题的扩展，作业车间调度问题(Job shop Scheduling Problem, JSP) 中每个工件可以有特定的工序安排，1976年Garey等^[1]证明了它是一个非确定性多项式(Non-deterministic Polynomial, NP) 难题。对于JSP，早期研究中大多采用的方法可分为近似方法和精确方法。其中近似方法以优先规则法^[2]和瓶颈移动法^[3]为代表，其求解过程较为复杂且计算量很大；而对于基准测试库^[4]中10工件10机器的问题，Applegate与Cook^[5]采用的分支定界法是非常有效的精确方法，但对规模更大的情形却不太适用。近年来许多元启发式算法相继提出，用于求解JSP的有遗传算法^[6]、模拟退火算法^[7]、粒子群算法^[8]、生物地理学优化算法^[9]等。遗传算法的主要优点是通用性强，它适用于各类优化问题^[10-13]，但在求解离散空间且具有NP特性的优化问题时容易陷入局部最优。通过引入多智能体协同理论，Zhong等^[14]提出了用于连续空间优化的多智能体遗传算法(Multiagent Genetic Algorithm, MAGA)，Sivasubramani和Swarup^[15]将多智能体差分算法用于电力系统的无功优化，改进后的算法不仅有良好的全局和局部寻优能力，且具有快速收敛性和较好的鲁棒性。
对于复杂的组合优化问题, 一般来说没有通用的算法框架，特别是对于解空间分布类似大山谷结构的JSP，采用单一算法往往难以找到问题的最优解，研究的趋势是将具有良好全局搜索能力的算法和局部搜索算法相结合^[16]。例如，Gao等^[17]结合遗传算法与变邻域算法求解JSP，Xia和Wu^[18]运用粒子群算法与模拟退火算法混合寻优。模拟退火算法是一种广泛应用的局部搜索算法，通过以一定概率接受劣解使得算法具有跳出局部最优的能力，寻优结果的好坏取决于退火进度表的选择和邻域解的产生机制。精细的退火进度表能够使寻优的效果更好，利用在马尔可夫链平稳分布下的目标函数均方差表达式，Romeo等^[19]成功推导出一种自适应退火策略。对于JSP的局部寻优而言，最早被提出且较为成功的邻域结构是由van Laarhoven等^[7]提出的N2结构，即通过交换关键路径上的任意2个相邻工序产生新解，他们证明了该结构与全局最优解的连通性，不足的是邻域解规模太大，实际操作中难以寻找到最优解。随后，Potts^[20]指出，要使得交换2个关键路径上的工序能够缩短加工时间，必要条件是待交换的2个工序中，满足前工序的工件紧前工序或者后工序的工件紧后工序在关键路径上。Balas和Vazacopoulos^[21]在此基础上提出了N6结构，该结构在操作过程中能翻转更多的析取弧，不仅能探索更大的空间而且限制了很多无效移动。
本文一方面针对JSP的NP特性，提出将MAGA用于问题的全局搜索，将所有染色体视作独立的智能体(agent) 并定义其相应的邻居环境，综合考虑编码的空间特性与解码的复杂性后采用基于工序的方式对染色体agent进行编码，并设计了邻居交互算子用于染色体agent之间的协同寻优以获得多个适应度较高的个体。另一方面，由于在工序编码下不同的染色体序列可能会被解码为同一调度以及解空间的大山谷特性，导致实现邻居交互操作过程中不仅会产生大量无效的操作也可能使得算法陷入局部最优，因此在全局搜索后，将每个染色体agent映射为一个JSP的非循环有向图，在N6邻域解生成机制的基础上引入自适应模拟退火算法(Adaptive Simulated annealing Algorithm, ASA) 进行局部优化。
1 JSP的析取图模型 JSP定义：N个工件在M台机器上加工，分别记作集合{J_i|i=1, 2, …, N}、{M_i|i=1, 2, …, M}，其中J_i为工件代号，M_i为机器代号。每个工件有特定的工艺，并给定每个工件使用机器的顺序及它在对应机器上的工序所需的加工时间，调度的具体内容就是确定每台机器上工件的加工顺序和每个工序的开工时间，使得最大完工时间(记作C_max) 最短，并假定：
1) 不同工件的工序之间没有顺序约束。
2) 某一工序一旦开始加工就不能中断，每台机器同一时刻只能加工一个工件，且机器不发生故障。
3) 所有零件均在零时刻到达，且在加工过程中经过每台机器且只经过一次。
常用的JSP模型有3种：Baker^[22]提出的整数规划模型、Adams等^[3]提出的线性规划模型以及Balas^[23]提出的析取图模型。本文通过交换关键工序块内的工序生成局部搜索的邻域解，因此采用析取图模型对JSP建模。以3×3的JSP为例(见表 1)，所对应的JSP析取图模型如图 1所示。表 1中的加工时间“2-3-6”表示工件J₁在机器序列“M₃-M₂-M₁”上分别所需的加工时间。
表 1 3工件3机器JSP Table 1 3-job 3-machine job shop scheduling problem

工件	机器序列	加工时间
J1	M3-M2-M1	2-3-6
J2	M1-M3-M2	4-5-2
J3	M2-M1-M3	3-5-4

表选项

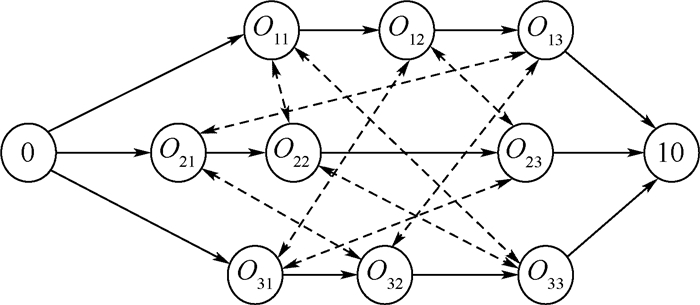图 1 析取图模型 Fig. 1 Disjunctive graph model

图选项

图 1中O_ik表示工件J_i的第k个工序，0和10是2个虚工序且加工时间为零，实线指向表示同一个工件的工序顺序关系；虚线即析取弧两端的工序表示在同一台机器上加工的工序，例如O₁₁、O₂₂、O₃₃都是在机器M₃上加工的。一个可行调度意味着确定每条析取弧指向(即每台机器上的工件排序)，形成一个非循环有向图，每条有向弧的弧长等于起点工序的加工时间，对应的关键路径(最长路径) 长度即为一个可行调度的最大完工时间。在进行JSP问题局部优化时，即寻找到合理的析取弧的指向，使得形成的非循环有向图的关键路径最短。
2 基于MAGA与ASA混合算法的JSP寻优 首先，结合多智能体协同理论对经典遗传算法进行改进，构建用于JSP全局搜索的MAGA，主要包括两部分内容：定义染色体agent的邻居环境，设计用于实现染色体agent间的竞争与合作的邻居交互算子。其次，考虑到MAGA局部寻优性能的不足，采用ASA对每个染色体agent开展局部搜索，从而得到一种新的混合算法框架。
2.1 定义染色体agent邻居环境 把每个染色体看作一个独立的agent，然后将其固定在一个网格环境中从而形成了每个染色体agent的邻居环境，如图 2所示^[14]。假设A_{i, j}代表格子坐标为(i，j) 的染色agent，则它的邻居集N_{i, j}被定义为

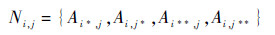(1)

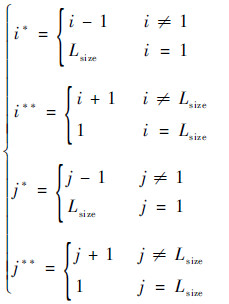(2)

式中：L_size为网格的维数。通过式(1) 与式(2) 可以找到每个染色体agent对应的4个邻居。例如处于网格中间的A_{2, 2}对应的邻居坐标为(1，2)、(2，1)、(2，3)、(3，2)，角点A_{1, 1}的邻居坐标为(L_size，1)、(1，L_size)、(2，L_size)、(L_size，2)。

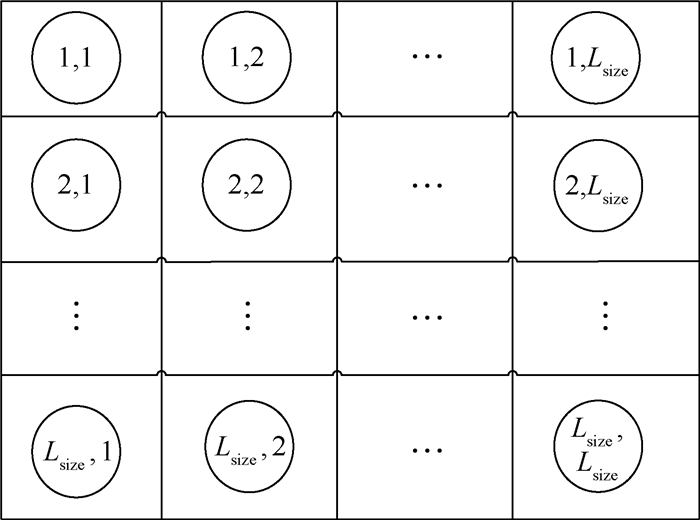图 2 多智能体网格系统[14] Fig. 2 Multiagent lattice system[14]

图选项

2.2 设计邻居交互算子 定义染色体agent邻居环境后，限定每个染色体agent只与它周围的4个邻居发生交互关系。为了避免邻居交互操作过程产生不可行解，同时又能够较好地保留父代的优良信息，采用基于工序的编码方式设计邻居交互算子，设计准则为以下两点：
1) 当个体与其4个邻居进行比较后，其适应度比邻居都要高，则它为一个赢家，相应的内容保持不变。
2) 当个体的适应度比4个邻居中最高适应度的个体要低，那么它便是一个输家，于是它将被适应度最高的邻居占领。
占领机制存在2种策略：一种认为个体虽然是输家，但它的信息还有用，于是执行合作策略，将其与最优邻居个体的信息进行融合得到的后代用于替代输家；另一种则为竞争策略即直接用最优邻居将其占领，再通过基本倒位变异产生新的后代。依概率P_c接受策略1，依概率1-P_c接受策略2。其中，策略1侧重于搜索的集中性，策略2侧重于搜索的分散性。
对于策略1，采用轮流交叉算子产生一个新的后代。假设失败个体A_{i, j}，并设最优邻居个体为B_{i, j}，交叉的步骤为：轮流从2个父代个体中选择基因，子代中第1个基因来自B_{i, j}，第2个基因来自A_{i, j}，这样依次进行下去，但若某个工件序号已经在子代出现了M次则后续不再选择该序号。例如，设失败个体为[4 2 1 2 3 4 2 3 1 1 1]，邻居最优个体为[2 1 4 1 2 4 3 2 1 3 4 3]，则执行策略1后的结果见图 3。

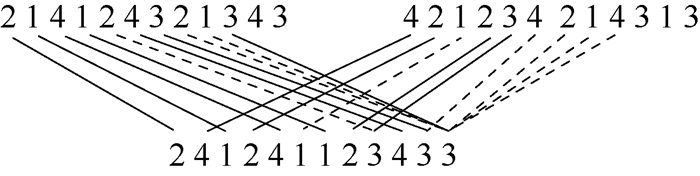图 3 轮流交叉算子 Fig. 3 Alternating position crossover operator

图选项

对于策略2，假设个体为[4 2 1 2 3 4 2 1 4 3 1 3]，采用基本倒位变异算子产生新的后代，则首先随机选择染色体中2个基因点位，随后将这2个基因点位内部的基因倒序，其他基因保持不变，产生的后代如图 4所示。

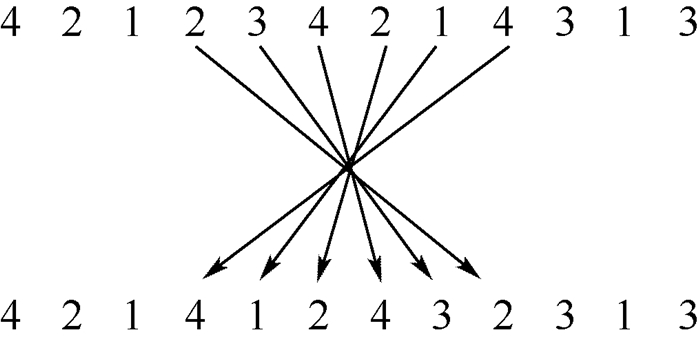图 4 基本倒位变异算子 Fig. 4 Simple inversion mutation operator

图选项

为了保持种群的多样性，在执行agent竞争与合作操作后，将移位变异算子引入agent交互算子的设计中，即依变异概率P_m随机选定的一个基因段进行整体移位来获取新的个体。例如给定染色体为[2 4 1 2 4 1 1 2 3 4 3 3]，由移位变异得到后代见图 5。

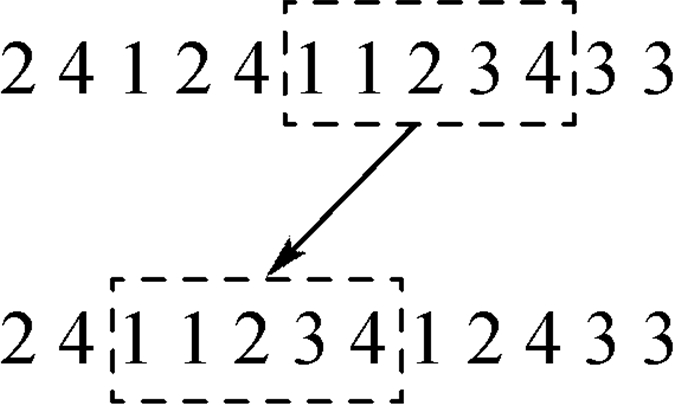图 5 移位变异算子 Fig. 5 Displacement mutation operator

图选项

邻居交互算子的核心在于利用少量个体进行协同寻优，通过赢家机制将优良个体保留，在占领机制中引入协作准则使得输家也可与最优个体交叉从而获得好的信息。
2.3 混合算法流程 通过构建MAGA框架用于JSP的全局搜索，并结合ASA用于局部寻优提出混合算法框架如图 6所示，其中C_hyb代表混合算法迭代次数，C_int代表agent交互操作次数。

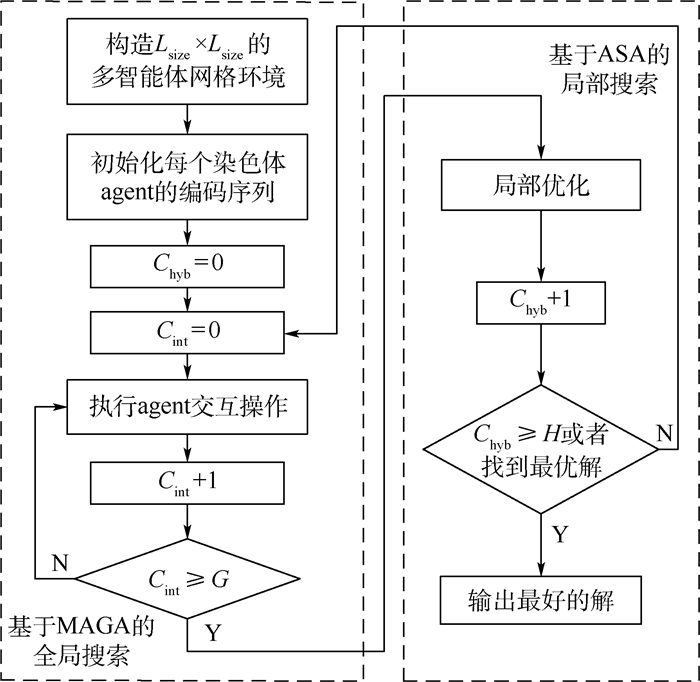图 6 混合多智能体遗传算法流程图 Fig. 6 Flowchart of hybrid MAGA

图选项

JSP寻优的具体步骤流程如下：
1) 构造多智能体网格环境
构造如图 2所示的多智能体的网格，形成所有染色体agent的邻居环境，其中L_size×L_size是指网格中的染色体agent的数目，将L_size的取值范围限定于5~10, 即群体的规模在25~100之间。
2) 初始化每个agent的编码序列
采用基于工序编码的方式初始化所有染色体agent。以表 1为例，可用序列[2 2 3 3 1 2 1 1 3]及其随机排列作为编码，序列中每个数字序号代表一个工件，同一个数字在染色体中数目为即该数字对应工件的工序数，从左到右遍历染色体时同一数字第几次出现则代表该工件第几道工序；另外为了使得解码空间更加贴近最优解，采用插入式策略^[10]进行主动解码，即依次取序列中的工序安排到相应的机器上，在满足约束的情况下尽可能地将每个工序提前开工。对于序列[2 2 3 3 1 2 1 1 3]的主动解码，在第2次取到1即安排工件J₁的第2个工序时，对应的机器M₂已经安排了工件J₃和J₂，可将其插入到工件J₂的前面，最后可解码得到C_max为15。
3) 执行agent交互操作
完成第1) 步和第2) 步的初始化后，计C_hyb为0，开始执行染色体agent交互操作循环，使网格中的每个染色体agent根据邻居交互算子与其4个邻居合作或者竞争来获取更优的信息，实现混合算法的全局搜索。
4) 判断agent交互操作次数C_int是否达到它的最大迭代次数G，若不满足则C_int增加1并回到第3) 步，否则执行第5) 步。
5) 对每个染色体agent进行局部搜索
针对基于工序编码下的遗传操作对于JSP局部搜索能力上不足，采用ASA进入局部搜索：首先通过N6结构产生新解，即依据Potts^[20]提出的准则并确保不会产生循环图，随机交换非循环有向图中的关键工序块内的工序(即处在关键路径上且在同一机器上加工的工序)，然后基于自适应降温策略展开局部寻优。获取局部优化初始解的过程为：先将染色体agent主动解码为一个可行调度，进而确立析取图模型中析取弧的方向后得到一个非循环有向图。
6) 判断是否满足混合算法的停机准则
停机准则设定为满足以下2个条件之一：混合算法迭代次数C_hyb达到它的最大迭代次数H；经过局部优化后的最优agent解码得到的最大完工时间等于已知最优解。若不满足停机准则C_hyb增加1并回到第3) 步(染色体agent编码序列由局部优化后的非循环有向图通过拓扑排序获得)；否则输出所有agent中最好的解，并结束算法。
3 实例验证 3.1 算法实现 算法采用VC++编程实现，主要的参数如下：
1) 全局搜索参数
为了使算法具有更好的全局搜索能力，应使策略1接受概率P_c取较小的值, 因此将P_c取为0.2。此外，染色体规模L_size×L_size=8×8=64，变异概率P_m=0.1，agent交互操作最大迭代次数G=20，混合算法最大迭代次数H=100。
2) 基于ASA局部搜索的参数
精细的冷却进度表能够使模拟退火算法在有限次的迭代过程中逼近问题的最优解，为此采用文献[19]提出的退火策略作为自适应降温函数:

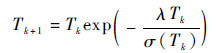(3)

式中：λ为固定的常数，取值于(0.5, 1.0]；σ(T_k) 为上一步迭代过程中适应度的样本标准差。将初始温度T₀设置为常数，取值范围在[10, 100]之间。ASA停止准则设定为在连续1个马尔可夫链中的目标函数值不再有变化。对于马尔可夫链的链长L，通常可取所有可行解的最大邻域解数目，且链长越大寻优结果越好，因此取之为相应实例的工序总数。
3.2 计算结果分析 选取基准测试库中的43个实例^[4]，包括Ft06、Ft10、Ft20以及La01~La40进行仿真计算，将算法运行20次后得到的最好结果与文献[6, 8, 17]对比，见表 2。实例规模中乘号前面是工件数，乘号后面是机器数。
表 2 计算结果对比 Table 2 Comparison of computational results

实例 代号	实例 规模	已知 最优解	最好结果
			新算法	文献[6]	文献[8]	文献[17]
Ft06	6×6	55	55	55	55	55
Ft10	10×10	930	930	930	930	930
Ft20	20×5	1 165	1 165	1 165	1 165	1165
La01	10×5	666	666	666	666	666
La02	10×5	655	655	655	655	655
La03	10×5	597	597	597	597	597
La04	10×5	590	590	590	590	590
La05	10×5	593	593	593	593	593
La06	15×5	926	926	926	926	926
La07	15×5	890	890	890	890	890
La08	15×5	863	863	863	863	863
La09	15×5	951	951	951	951	951
La10	15×5	958	958	958	958	958
La11	20×5	1 222	1 222	1 222	1 222	1 222
La12	20×5	1 039	1 039	1 039	1 039	1 039
La13	20×5	1 150	1 150	1 150	1 150	1 150
La14	20×5	1 292	1 292	1 292	1 292	1 292
La15	20×5	1 207	1 207	1 207	1 207	1 207
La16	10×10	945	945	945	945	945
La17	10×10	784	784	784	784	784
La18	10×10	848	848	848	848	848
La19	10×10	842	842	842	842	842
La20	10×10	902	902	907	902	902
La21	15×10	1 046	1 046	1 052	1 046	1 046
La22	15×10	927	927	930	927	927
La23	15×10	1 032	1 032	1 032	1 032	1 032
La24	15×10	935	938	941	941	940
La25	15×10	977	977	977	977	984
La26	20×10	1 218	1 218	1 218	1 218	1 218
La27	20×10	1 235	1 235	1 246	1 239	1 261
La28	20×10	1 216	1 216	1 216	1 216	1 216
La29	20×10	1 152	1 175	1 165	1 173	1 190
La30	20×10	1 355	1 355	1 355	1 355	1 355
La31	30×10	1 784	1 784	1 784	1 784	1 784
La32	30×10	1 850	1 850	1 850	1 850	1 850
La33	30×10	1 719	1 719	1 719	1 719	1 719
La34	30×10	1 271	1 271	1 271	1 271	1 271
La35	30×10	1 888	1 888	1 888	1 888	1 888
La36	15×15	1 268	1 285	1 279	1 278	1 281
La37	15×15	1 397	1 397	1 407	1 397	1 431
La38	15×15	1 196	1 196	1 213	1 208	1 196
La39	15×15	1 233	1 240	1 244	1 233	1 241
La40	15×15	1 222	1 224	1 233	1 225	1 233

表选项






由表 2可知，在所有43个实例中，新算法有5个实例未找到最优解，文献[6]分别有11、6、88个实例未找到最优解。进一步定义43个实例的平均寻优偏差δ计算式为

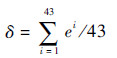(4)

式中：eⁱ为第i行实例寻优偏差，计算式如下：

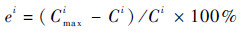(5)

其中：C_maxⁱ为对应算法找到的最好结果; Cⁱ为相应实例的已知最优解。
计算结果表明，新算法与文献[6]的平均寻优偏差分别为0.102 1%、0.207 2%、0.114 8%、0.256 1%，新算法的整体寻优效果更好。并且：
1) 与文献[6]相比，对于Ft06、Ft10、Ft20与La01~La19、La23、La25、La26、La28、La30~La35共32个实例，新算法与之均能找到最优解。对于剩下11个实例，新算法能找到9个更好的解，并且La20、La21、La22、La27、La37、La38为最优解。
2) 与文献[8]相比，对于Ft06、Ft10、Ft20与La01~La23、La25、La26、La28、La30~La35、La37共36个实例，新算法与之均能找到最优解。对于剩下7个实例，新算法能找到4个更好的解，并且La27、La38为最优解。
3) 与文献[17]相比，对于Ft06、Ft10、Ft20与La01~La23、La26、La28、La30~La35、La38共35个实例新算法与之均能找到最优解。对于剩下8个实例，新算法能找到7个更好的解，并且La25、La27、La37为最优解。
为了进一步说明新算法寻优效果，以La27为例，绘制找到的最优调度甘特图如图 7所示。图 7中每个方框代表一个工件的相应工序，方框长度代表其加工时间，并标明其所属工件。由图 7可见，对应的最后完工的工序是在机器M₂上的工件J₅，最大完工时间为1 235，比文献[6]更优。

图 7 La27的调度甘特图 Fig. 7 Gantt chart of La27

图选项

4 结论 作业车间调度是实施生产计划的重要环节，作为经典的组合优化难题，一直以来受到学术界的广泛关注。本文针对作业车间调度问题的非确定性多项式特性与解空间分布的大山谷属性，提出了一种多智能体遗传算法与自适应模拟退火算法融合的混合优化算法，并结合实例分析得出以下结论：
1) 新算法融入多智能体协同理论将每一个染色体视作独立的智能体，在邻居交互算子的设计中，采用赢家机制保留优良的个体，在占领机制中引入协作准则使得适应度较低的个体也能够提供有用的信息，提高了算法的收敛速率，能够快速地找到多个适应度较高的可行解，具有更好的全局搜索效率。
2) 采用插入式解码方式对智能体解码获得主动调度，保证了最优调度的存在，并进一步考虑到工序编码方式下的遗传操作的局限性，将其映射到一个非循环有向图作为局部优化的初始解，结合自适应模拟退火算法对每个智能体进一步优化，避免了算法陷入局部最优。
3) 通过选取基准测试库中的43个实例进行算法对比，计算结果验证了新算法的有效性和优越性。

参考文献

[1]	GAREY M R, JOHNSON D S, SETHI R. The complexity of flowshop and job shop scheduling[J].Mathematics of Operations Research, 1976, 1(2): 117–129.DOI:10.1287/moor.1.2.117
[2]	GIFFLER B, THOMPSON G L. Algorithms for solving productionscheduling problems[J].Operations Research, 1960, 8(4): 487–503.DOI:10.1287/opre.8.4.487
[3]	ADAMS J, BALAS E, ZAWACK D. The shifting bottleneck procedure for job shop scheduling[J].Management Science, 1988, 34(3): 391–401.DOI:10.1287/mnsc.34.3.391
[4]	BEASLEY J E. OR-library:Distributing test problems by electronic mails[J].Journal of Operation Research Society, 1990, 41(11): 1069–1072.DOI:10.1057/jors.1990.166
[5]	APPLEGATE D, COOK W. A computational study of the job shop scheduling problem[J].ORSA Journal on Computing, 1991, 3(2): 149–156.DOI:10.1287/ijoc.3.2.149
[6]	赵诗奎, 方水良, 顾新建. 作业车间调度的空闲时间邻域搜索遗传算法[J].计算机集成制造系统, 2014, 20(8): 1930–1940.ZHAO S K, FANG S L, GU X J. Idle time neighborhood search genetic algorithm for job shop scheduling[J].Computer Integrated Manufacturing Systems, 2014, 20(8): 1930–1940.(in Chinese)
[7]	VAN LAARHOVEN P J M, AARTS E H L, LENSTRA J K. Job shop scheduling by simulated annealing[J].Operations Research, 1992, 40(1): 113–125.DOI:10.1287/opre.40.1.113
[8]	LIN T L, HORNG S J, KAO T W, et al. An efficient job-shop scheduling algorithm based on particle swarm optimization[J].Expert Systems with Applications, 2010, 37(3): 2629–2636.DOI:10.1016/j.eswa.2009.08.015
[9]	WANG X, DUAN H B. A hybrid biogeography-based optimization algorithm for job shop scheduling problem[J].Computers & Industrial Engineering, 2014, 73: 96–114.
[10]	CHENG R, GEN M, TSUJIMURA Y. A tutorial survey of job shop scheduling problems using genetic algorithms-I.Representation[J].Computers & Industrial Engineering, 1996, 30(4): 983–997.
[11]	GORDINI N. A genetic algorithm approach for SMEs bankruptcy prediction:Empirical evidence from Italy[J].Expert Systems with Applications, 2014, 41(14): 6433–6445.DOI:10.1016/j.eswa.2014.04.026
[12]	KUMAR K S, PAULRAJ G. Genetic algorithm based deformation control and clamping force optimisation of workpiece fixture system[J].International Journal of Production Research, 2011, 49(7): 1903–1935.DOI:10.1080/00207540903499438
[13]	陶杨, 韩维. 基于改进多目标遗传算法的舰尾紊流模拟方法[J].北京航空航天大学学报, 2015, 41(3): 443–448.TAO Y, HAN W. Carrier airwake simulation methods based on improved multi-objective genetic algorithm[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(3): 443–448.(in Chinese)
[14]	ZHONG W C, LIU J, XUE M Z, et al. A multiagent genetic algorithm for global numerical optimization[J].IEEE Transactions on Systems, Man, and Cybernetics, Part B:Cybernetics, 2004, 34(2): 1128–1141.DOI:10.1109/TSMCB.2003.821456
[15]	SIVASUBRAMANI S, SWARUP K S. Multiagent based differential evolution approach to optimal power flow[J].Applied Soft Computing, 2012, 12(2): 735–740.DOI:10.1016/j.asoc.2011.09.016
[16]	BLUM C, ROLI A. Metaheuristics in combinatorial optimization:Overview and conceptual comparison[J].ACM Computing Surveys (CSUR), 2003, 35(3): 268–308.DOI:10.1145/937503
[17]	GAO L, ZHANG G H, ZHANG L P, et al. An efficient memetic algorithm for solving the job shop scheduling problem[J].Computers & Industrial Engineering, 2011, 60(4): 699–705.
[18]	XIA W, WU Z. An effective hybrid optimization approach for multi-objective flexible job-shop scheduling problems[J].Computers & Industrial Engineering, 2005, 48(2): 409–425.
[19]	HUANG M D, ROMEO F, SANGIOVANNI V A K.Efficient general cooling schedule for simulated annealing[C]//Proceeding of IEEE International Conference on Computer Aided Design.Piscataway, NJ:IEEE Press, 1986:381-384.
[20]	POTTS C N. Analysis of a heuristic for one machine sequencing with release dates and delivery times[J].Operations Research, 1980, 28(6): 1436–1441.DOI:10.1287/opre.28.6.1436
[21]	BALAS E, VAZACOPOULOS A. Guided local search with shifting bottleneck for job shop scheduling[J].Management Science, 1998, 44(2): 262–275.DOI:10.1287/mnsc.44.2.262
[22]	BAKER K R. Introduction to sequencing and scheduling[M].New York: John Wiley & Sons, 1974.
[23]	BALAS E. Machine scheduling via disjunctive graphs:An implicit enumeration algorithm[J].Operation Research, 1969, 17(6): 941–957.DOI:10.1287/opre.17.6.941