可满足性问题(Satisfiability Problem, SAT)是一种特殊的约束满足问题(Constraint Satisfaction Problem, CSP)，它是计算机和数理学界众多****关注的一个重大问题。现实世界中，很多重要且难以解决的验证和组合优化问题都可以转化为SAT问题。研究者已从计算复杂性、相变现象、难解实例产生模型和判定算法等方面对该问题开展了大量的研究，并为进一步认识SAT问题的难解本质、构造SAT难解实例、设计及测试高效的SAT判定算法奠定了一定的基础。
在SAT问题中，子句长度为k的SAT判定问题称为k-SAT问题。当k≥3时，k-SAT问题是第一个被证明了的NP完全问题^[1]。众多****以SAT问题的NP完全性为种子，借助于多项式规约转换技术，发现了许多组合优化问题都是NP完全问题，而将这类组合优化问题转化为SAT判定问题，然后再利用现有的SAT判定工具来求解，往往比求解原问题更为简单^[2]。当前，SAT问题特别是3-SAT问题仍然是计算复杂性中的一个核心问题。
在随机k-SAT问题中，子句个数M与变元个数N的比值α(也称约束密度)是一个重要的结构参数，该参数不仅会影响到公式的可满足性，还会影响到公式的判定难度^[3-4]。具体地说，对于给定的较大规模的变元数N，随着子句变元比α的不断增大，存在某个临界值点α_s(k)，当α < α_s(k)时，几乎所有的随机k-SAT实例都是可满足的，而当α > α_s(k)时，几乎所有的随机k-SAT实例都是不可满足的。这种现象被称为随机k-SAT问题的相变(phase transition)现象。另外，从算法角度来看，在远离临界值点α_s(k)的两侧，绝大部分实例都是易解的，而在临界值点α_s(k)附近，从统计物理学的角度来看，由于随机k-SAT公式的解空间被分解成许多较小的解集簇，且这些解集簇之间相互分离，在每个解集簇内，存在着大量的冻结变元^[5-7]，不可能通过翻转这个解集簇中的某个可满足指派的少量变元赋值而使其转化为另一个解集簇中的可满足指派。因此，在临界值点α_s(k)附近，几乎所有的k-SAT求解算法都表现出了较差的性能，即便是采用当前求解k-SAT问题最为有效的调查传播(Survey Propagation, SP)算法^[8-9]，其在求解α_s(k)附近的k-SAT实例时，也往往会失效。因此，研究k-SAT问题的相变现象不仅有助于进一步理解NP完全问题的难解本质，还有助于激发人们设计更为有效的SAT求解算法。然而，要找出k-SAT问题的确切相变点却是非常困难的。
当前，在SAT问题相变性质的研究方面，仅知道2-SAT^[10]、k-NAESAT^[11]、Regular 2-SAT^[12]、Regular NAE-SAT^[13]以及k-XORSAT^[14]等几种具有特殊规则结构的SAT问题的精确相变点。Mertens等^[15]运用统计物理中的一阶复本对称破缺理论，预测随机k-SAT问题可满足的临界值点α_s(k)=2^kln 2-(ln 2+1)/2+o_k(1)。在此基础上，Coja-Oghlan^[16]与Ding等^[17]通过寻找随机k-SAT问题中解的聚类，分别证明了当k足够大时α_s(k)的渐近值，即α_s(k)~2^kln 2-(ln 2+1)/2+o_k(1)，这与文献[16]的预测几乎吻合。
在一般的随机3-SAT问题中，尽管人们不知道α_s的确切值，但研究表明，α_s至少为3.520^[18]，至多为4.506^[19]。Mézard等^[8-9]预测α_s的值为4.267，且存在阈值α_c?3.921，并称α < α_c的区域为易解SAT区域，而α_c < α < α_s的区域被称为难解SAT区域。
难解区域中的难解实例不仅能被广泛应用于各种NP完全问题的算法性能测试，还与密码学领域中的单向函数(one-way function)等密切相关^{[3, 20]}。因此，众多****对如何构造CSP中的难解实例开展了大量的研究。北京航空航天大学的许可教授等^[21-22]分别在B模型和D模型的基础上提出的具有精确相变点的RB模型及RD模型，解决了经典CSP模型的平凡无解性问题，已被广泛应用于构造CSP、SAT和最大团等问题的难解实例^[23]。
此外，在SAT问题的研究中，研究者常常通过对公式结构中的子句长度、变元出现次数等加以限制，从而得到某种规则结构的SAT问题，使得在保留NP完全性的公式子类中SAT问题的研究更为具体。如限制子句长度为k的k-SAT问题，Tovey^[24]提出的变元出现次数受界的SAT判定问题；Dubois^[25]提出的每个子句恰有r个不同文字，每个变元至多出现s次的r, s-SAT问题；许道云教授^[26]提出的利用极小不可满足公式的临界特性，将任意一个3-SAT问题多项式时间规约到每个变元恰好出现4次的规则3-SAT问题；特别地，Boufkhad等^[12]提出的随机正则k-SAT问题，受到了广泛的关注^{[16, 27-31]}。
在随机正则3-SAT问题的相变性质方面，Boufkhad等^[12]首先证明了随机正则3-SAT问题可满足的临界值点α_3r位于2.46~3.78之间，即该相变点在均匀随机3-SAT问题相变点的左侧，也就是说，相对于一般的均匀随机3-SAT实例，随机正则3-SAT实例更难满足。此外，Rathi等^[27]利用一阶矩方法和二阶矩方法证明了随机正则k-SAT问题可满足临界值点α_kr的上界和下界，即2^kln2-(k+1) ln 2/2-1≤α_kr≤2^kln 2。
本文重点研究随机正则3-SAT问题的一个子问题--严格随机正则(3, s)-SAT问题。给出严格随机正则(3, s)-SAT问题的实例产生模型--SRR模型，并证明严格随机正则(3, s)-SAT问题在s>11时是高概率不可满足的。实验结果表明：严格随机正则(3, s)-SAT实例的相变点位于s=11处，且当s=11时，SRR模型所产生的随机实例比在相变点α_s?4.267处同规模的均匀随机3-SAT实例更难求解，因此，本文所提出的SRR模型能够较容易地构造s=11处的随机3-SAT难解实例。
1 严格随机正则(3, s)-SAT问题 1.1 基本概念 令{x₁, x₂, …, x_N}为含有N个布尔变元的集合，一个文字?_i是一个变元x_i或其否定?x_i，一个子句C是若干个文字的析取(?₁∨?₂∨…∨?_k)。一个CNF (Conjunctive Normal Form)公式F是若干个子句的合取(C₁∧C₂∧…∧C_M)。一个k-CNF公式是由N个变元和M个长度恰好为k的子句构成的CNF公式。给定一个CNF公式F，SAT问题指：是否存在一组变元{x₁, x₂, …, x_N}的赋值，使得公式F为真，其中k-CNF公式的判定问题称为k-SAT问题。一个正则3-SAT问题^[12]是一个具有N个变元，M个子句并满足如下限制的3-CNF公式的判定问题：每个子句的长度恰有3个不同文字，每个变元恰好出现s次，且其正负文字出现的期望次数相等。
定义1??严格正则(3, s)-SAT问题
严格正则(3, s)-SAT问题是正则3-SAT问题的子问题，在这类公式中，每个子句恰有3个不同文字，每个变元恰好出现s(s∈Z⁺)次且其正负文字出现至多相差1次。
一个严格随机正则(3, s)-SAT公式是指均匀地从所有严格正则(3, s)-SAT公式上选取的一个随机实例，其对应的因子图^[32]是一个双正则二部图，其中，二部图中的一侧由变元集构成，另一侧由子句集构成。通常用实心圆点来表示变元节点，用矩形框来表示子句节点，若变元x_i在子句C_i中正出现，则用实边连接x_i与C_i，否则就用虚边连接x_i与C_i。例如，严格正则(3, 4)-SAT公式F=(?x₁∨?x₂∨x₃)∧(?x₁∨x₂∨?x₃)∧(x₁∨?x₂∨x₃)∧(x₁∨x₂∨?x₃)的因子图为图 1所示的双正则二部图。图中：C₁=(?x₁∨?x₂∨x₃)，C₂=(?x₁∨x₂∨?x₃)，C₃=(x₁∨?x₂∨x₃)，C₄=(x₁∨x₂∨?x₃)，且每个变元恰好出现4次，每个文字恰好出现2次。

图 1 严格正则(3, 4)-SAT公式F的双正则二部图表示 Fig. 1 Biregular bigraph representation of strictly regular (3, 4)-SAT formula F

图选项

1.2 随机k-SAT的相变现象 大量的理论研究和实验结果表明，在通过某种随机过程产生的某些NP完全问题实例中，往往会存在某个控制参数μ，使得当随机实例中变元规模较大时，存在某个临界值点μ^*，当μ>μ^*时，几乎所有的实例都是无解的，而当μ < μ^*时，几乎所有的实例都是有解的，这种现象被称为相变现象，临界值点μ^*被称为相变点。此外，实验结果还表明，此类问题中，最难解的实例往往位于相变点附近的区域。
在随机k-SAT问题中，当变元规模N→∞时，对于给定的变元规模N和子句长度k，随机选择一个k-SAT式F，其可满足的概率Pr (F is SAT)是子句变元比α的减函数。实验研究表明^[33]，存在一个临界值点α_s(k)，当α < α_s(k)时，几乎所有随机k-SAT实例都是可满足的，而当α_s(k)时，几乎所有的随机k-SAT实例都是不可满足的，其形式化为

(1)

尽管人们普遍相信式(1)对于任意的k≥2都是成立的，然而在求解精确的临界值点α_s(k)方面，经过众多研究者的努力，虽然已取得了很大的进步，但当前，式(1)仅在k=2^[10]时得到了严格的证明，在k足够大时，得到了α_s(k)的渐近值^[16-17]。因此，研究某种更为具体的规则结构的随机k-SAT子问题，例如严格随机正则(3, s)-SAT问题是比较有意义的。
2 严格随机正则(3, s)-SAT实例产生模型 通常的均匀随机3-SAT问题的实例产生模型是指：独立并且均匀地从所有2³C_N³个长度为3的子句中随机选取M=αN个可能子句，从而构成一个随机3-SAT公式。下面我们介绍严格随机正则(3, s)-SAT问题的实例产生模型--SRR模型。该模型包含变元规模N和变元出现次数s 2个参数，在SRR模型产生的子句中，每个子句恰有3个不同文字，每个变元都恰好出现s次且其正负文字出现次数r至多相差1次，不难发现，在严格随机正则(3, s)-SAT问题实例中，变元总数N为3的整数倍，子句总数M恰为Ns/3个，且子句变元比α=M/N=s/3。令r_i1表示文字正出现的次数，r_i2表示文字负出现的次数。下面给出SRR模型生成严格随机正则(3, s)-SAT问题实例的具体过程。
Step 1??置j=0，C=?。
Step 2??对每个变元x_i，i∈(1，2，…，N)：
Step 2.1??若s为偶数，则置r_i1=r_i2=s/2；
Step 2.2??若s为奇数，等概率地置r_i1=└s/2┘或r_i1=└s/2┘+1，并置r_i2=s-r_i1；
Step 2.3??产生r_i1个正文字的拷贝、r_i2个负文字的拷贝放置于盒子A中。
Step 3??从A中不放回地随机选取3个文字?_j1，?_j2，?_j3：
Step 3.1??若?_j1, ?_j2, ?_j3对应的变元互不相同(可以构成一个合法的子句)且?_j1, ?_j2, ?_j3不同时出现在已有的某个子句C_k(k=1，2，…，j)中(不是重复子句)，则置C_j=?_j1∨?_j2∨?_j3，并将子句C_j以合取的方式连接到C中；
Step 3.2??否则将?_j1, ?_j2, ?_j3放回A中，返回Step 3；
Step 3.3??置A=A{?_j1, ?_j2, ?_j3}，j=j+1。
Step 4??若j < Ns/3，返回Step 3，否则输出C并结束处理。
3 严格随机正则(3, s)-SAT问题相变点上界 本节结合一阶矩方法和生成函数展开项系数的渐近近似技术，证明严格随机正则(3, s)-SAT问题相变点的上界。
令Z为一个非负随机变元且其期望为E(Z)，则由一阶矩方法有

(2)

若表示一个严格随机正则(3, s)-SAT公式F可满足的解的个数，那么由式(2)有

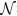
(3)

对于F中的任意一个指派σ(x₁, x₂, …, x_N)，令表示事件：指派σ(x₁, x₂, …, x_N)满足公式F；令表示事件：指派σ(1，1，…，1)满足公式F。由SRR模型的生成机制知，对变元集{x₁, x₂, …, x_N}中的任何指派，其能成为一个可满足解的概率是相同的，因此有成立。由于N个变元的所有指派数共有2^N个，所以结合式(3)有

(4)

下面计算σ(1，1，…，1)满足一个严格随机正则(3, s)-SAT公式F的概率。由生成函数的性质知，每个子句中至少含有1个正文字的生成函数为

(5)

由SRR模型的产生机制知，其所产生的公式中正文字的总数和负文字的总数均为Ns/2个，由于所有M=Ns/3个子句中每个子句都至少含有1个正文字的生成函数为p(x)^M，即

(6)

令λ表示公式中M个子句均能被满足的公式总数，则由生成函数的性质知，λ为p(x)^M的展开项中x^Ns/2项的系数。记：λ=[x^Ns/2]{p(x)^M}。令f(x)=p(x)/x=3+3x+x²，由M=Ns/3知

(7)

下面采用文献[34]中关于生成函数展开项系数的渐近近似技术，来求解f(x)^M的展开项中x^M/2项的系数，即计算式(7)中λ的值。
引理1^[34] ??令f(x)=f₀+f₁x+f₂x²+…，其是一个满足f₀≠0，f₁≠0且f_i≥0(i≥2)的生成函数，定义Δf(x)和δf(x)为f(x)上的2个操作算子，且Δf(x)=xf′(x)/f(x)，δf(x)=Δf′(x)/x，假设γ, η→∞且γ/η是区间[a, b](0 < a < b)上的常数，定义ρ和σ²分别满足Δf(ρ)=γ/η，σ²=ρ²δf(ρ)，若ρ>0，则

(8)

定理1 ??若s>11，则SRR模型所生成的严格随机正则(3, s)-SAT实例是高概率不可满足的。
证明 ??由f(x)=3+3x+x²，γ=M/2，η=M，由引理1有

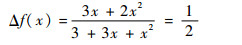(9)

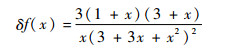(10)

则由式(7)和式(8)有

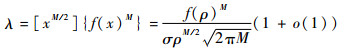(11)

由于严格随机正则(3, s)-SAT公式中所有正文字的排列和负文字的排列均有(Ns/2)!个，且总的公式数为(Ns)!个，则σ(1，1，…，1)满足一个随机公式F的概率为

(12)

进一步计算一个随机公式可满足的解的个数的期望值，由式(4)和式(12)有

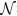
(13)

由Stirling公式^[35]有

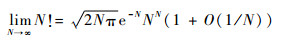(14)

则由式(13)和式(14)有

定义E()的熵密度为，则

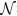
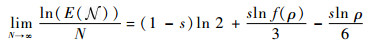(15)

由式(9)得ρ=(5-1)/2，则f(ρ)=5+3。由式(10)知δf(ρ)=(15+95)/(2+25)。另外，由σ²=ρ²δf(ρ)知σ=35/2。
令函数，有

(16)

则，由g′(s) < 0知g(s)是关于s的单调递减函数，又因为g(11)≈0.021 2>0，g(12)≈-0.039 9 < 0，因此，由s∈Z⁺知当s>11时，，结合式(3)知，SRR模型所生成的严格随机正则(3, s)-SAT实例是高概率不可满足的。
证毕
4 实验分析 本节通过实验观察严格随机正则(3, s)-SAT问题的相变点，并比较求解该问题在相变点处的实例与求解均匀随机3-SAT问题在相变点处的实例难度，以说明SRR模型所构造的在相变点处的3-SAT实例比均匀随机3-SAT模型构造的相变点处的实例更难解。
由于SAT问题的树型归结证明长度与基于归结的算法的运行时间有密切关系，Chvátal和Szemerédi^[36]已经证明了随机k-SAT问题在k≥3时具有指数级的树型归结证明，即基于归结的算法在求解随机3-SAT问题中的时间开销呈指数增长。此外，由于当前求解SAT问题的较好的完备算法如DPLL^[37]及其改进版本ZChaff^[38]都是基于归结的算法，因此，在实验中选用ZChaff算法来求解这2种随机3-SAT实例，用以比较这2种实例的求解难度。
1)针对严格随机正则(3, s)-SAT问题，选取变元规模N分别为60，90，…，210，各变元出现次数s分别取7，8，…，15，并用SRR模型对每个变元规模中的每个s产生100个随机实例(共6×9×100个实例)。然后采用ZChaff算法计算各变元规模下的9×100个实例，同时记录下求解每个实例的运行时间和可满足情况。表 1列出了不同变元规模下，s取不同值时每100个随机实例中可满足的实例总数。表 2列出了不同变元规模下，s取不同值时每个随机实例的平均求解时间。
表 1 各变元规模下，不同s时每100个严格随机正则(3, s)-SAT实例中可满足的实例总数 Table 1 Total number of satisfied instances for each s in every 100 strictly regular random (3, s)-SAT instances with different-sized variables

s	7	8	9	10	11	12	13	14	15
N=60	100	100	100	84	43	0	0	0	0
N=90	100	100	100	94	33	0	0	0	0
N=120	100	100	100	95	30	0	0	0	0
N=150	100	100	100	100	17	0	0	0	0
N=180	100	100	100	100	14	0	0	0	0
N=210	100	100	100	100	13	0	0	0	0

表选项






表 2 各变元规模下，不同s时每100个严格随机正则(3, s)-SAT实例中各实例的平均求解时间 Table 2 Average solution time for each s in every 100 strictly regular random (3, s)-SAT instances with different-sized variabless

s	9	10	11	12	13
N=60	0.002 4	0.031 5	0.029 2	0.028 6	0.017 6
N=90	0.004 5	0.206 7	0.438 4	0.167 3	0.107 9
N=120	0.008 8	2.493 7	4.854 1	1.436 4	0.595 1
N=150	0.045 0	10.943 7	109.409 0	15.267 6	5.454 7
N=180	0.090 4	124.586 9	1 760.378 0	219.243 4	30.070 8
N=210	0.150 6	747.547 3	57 679.600 0	4 080.987 0	485.358 0

表选项






从表 1可以看出，当变元规模N≥60且各变元出现次数s≥12时，在所有随机生成的严格随机正则(3, s)-SAT实例中，均未发现可满足的实例，这与定理1中的结论完全吻合。
此外，当变元规模N≥60且各变元出现次数s≤9时，在所有随机生成的严格随机正则(3, s)-SAT实例中都未发现不可满足的实例，并且在s=10时，随着变元规模N的增大，随机生成的严格正则(3, 10)-SAT实例中可满足实例的数目也逐渐增多，且当变元规模N达到150以后，所有的严格随机严格正则(3, 10)-SAT实例都是可满足的，而在s=11时，实验中发现，既有不可满足的实例，也有可满足的实例。
因此，由实验可以看出，当变元规模N较大时，严格随机正则(3, s)-SAT问题在s>11时，所有随机生成的实例都是高概率不可满足的，而当s < 11时，所有严格随机正则(3, s)-SAT问题都是高概率可满足的，即严格随机正则(3, s)-SAT问题的精确相变点位于s=11处。
图 2给出了不同变元规模下严格随机正则(3, s)-SAT实例在不同变元出现次数下，其可满足的概率。可以看出，随着变元规模N的逐渐增大，(3, 10)-SAT实例逐渐变为全部可满足，而当变元规模N≥60时，(3, 12)-SAT实例全部变为不可满足，即严格随机正则(3, s)-SAT问题的精确相变点位于s=11处。

图 2 不同变元规模下严格随机正则公式的相变 Fig. 2 Phase transition for strictly regular random formulas with different-sized variables

图选项

记s=11处求解单个实例的平均求解时间为t，由表 2知，当问题规模N≤120时，即使是在相变点s=11处的严格随机正则(3, s)-SAT实例，其单个实例的平均求解也可以在5 s内完成，而当N=150时，t=109.409 0s，当N=180时，t=1 760.378 0 s，随着问题规模的进一步增大，求解s=11处单个实例的平均求解时间也迅速增加，当N=210时，求解s=11处单个实例的平均求解时间已高达57 679.600 0 s。
图 3给出了变元规模N=150，180，210时，s分别取9，10，…，13时每100个随机实例中各实例的平均求解时间。可以看出，当s≤9和s≥13时，严格随机正则(3, s)-SAT问题实例相对较易求解。另一方面，从图 3还可以看出，求解严格随机正则(3, s)-SAT问题实例的难度与求解均匀随机3-SAT问题实例的情形类似，也呈现出典型的“Easy-Hard-Easy”模式，且在相变点右侧区域的实例相对于相变点左侧区域的实例而言，求解难度要更大一些。

图 3 不同变元规模下严格随机正则(3, s)-SAT实例的平均求解时间 Fig. 3 Average solution time for strictly regular random (3, s)-SAT instances with different-sized variables

图选项

2)针对通常的均匀随机3-SAT问题，分别选取变元规模N为60，90，…，270，对子句变元比α，选取其初始值α_start=2，步长Δα=0.05且α_end=6，然后采用均匀随机3-SAT实例产生模型，对不同变元规模下的每个α，各生成100个随机实例。实验过程中，仍采用ZChaff算法对每种变元规模下的100(α_end-α_start)/Δα=8 000个实例(共计8×8 000个实例)进行求解，并记录求解每个实例的运行时间和可满足情况。
由于α < 3.95时，绝大多数的随机3-SAT实例都是可满足的，而α>4.55时绝大多数的实例都是不可满足的，因此，在表 3中只给出了不同变元规模下，α取3.95~4.55时每100个随机实例中可满足的实例总数。另外，当变元规模N≤120时，随机3-SAT实例在相变点附近也较易求解，所以在表 4中只给出了变元规模N取150，180，…，270且α?4.267下每100个随机3-SAT实例中每个实例的平均求解时间。
表 3 各变元规模下，相变点附近每100个均匀随机3-SAT实例中可满足的实例总数 Table 3 Total number of satisfied instances near phase transition point in every 100 uniform random 3-SAT instances with different-sized variables

α	3.95	4.05	4.15	4.20	4.25	4.30	4.35	4.45	4.55
N=60	91	84	68	67	62	55	42	35	19
N=90	94	89	72	61	61	45	40	35	8
N=120	94	90	74	64	61	40	37	21	6
N=150	95	91	78	64	57	52	46	18	8
N=180	100	91	76	64	48	44	33	19	5
N=210	100	93	81	70	50	47	30	12	0
N=240	99	99	78	73	50	35	25	12	2
N=270	100	98	88	69	61	48	23	13	0

表选项






表 4 各变元规模下，α?4.267时每100个均匀随机3-SAT实例中各实例的平均求解时间 Table 4 Average solution time for α?4.267 in every 100 uniform random 3-SAT instances with different-sized variables

N	150	180	210	240	270
平均求解时间/s	1.341 7	8.293 5	76.859 0	361.543 4	2 548.435 0

表选项






由于严格随机正则(3, s)-SAT公式的子句变元比α=s/3，将图 2中s用对应的子句变元比来表示，结合实验中所有随机生成的均匀随机3-SAT实例的求解结果，得到了如图 4所示的随机3-SAT与严格随机正则(3, s)-SAT问题的相变。图中：N_R为正则公式的变元数。可以看出，相对于一般的3-SAT问题，严格随机正则(3, s)-SAT问题的相变点有明显的前移现象，也就是说，严格随机正则(3, s)-SAT问题实例比一般的均匀随机3-SAT问题实例更难满足。

图 4 不同变元规模下均匀随机3-SAT实例和严格随机正则(3, s)-SAT实例的相变 Fig. 4 Phase transitions for uniform random 3-SAT instances and strictly regular random (3, s)-SAT instances with different-sized variables

图选项

通过比较表 2和表 4中同规模下，在相变点s=11处的严格随机正则(3, s)-SAT和在相变点α?4.267处的均匀随机3-SAT的实例的平均求解时间，可以看出，在变元规模N=150时，求解相变点s=11处的严格随机正则(3, s)-SAT问题实例的平均时间t₁=109.409 0 s，而求解同规模的均匀随机3-SAT问题实例仅需要t₂=1.341 7 s，当N=180，t₁=1 760.378 0 s，t₂=8.293 5 s，当N=210时，t₁=57 679.600 0 s，t₂=76.859 0 s。特别地，即使求解规模N=270时的相变点处的均匀随机3-SAT问题实例，其平均求解时间t₂也仅仅为2 548.435 0 s，这个平均求解时间甚至远小于求解规模N仅为210的严格随机正则(3, s)-SAT实例的平均求解时间。因此，在基于归结的算法上，求解严格随机正则(3, s)-SAT问题实例要远比求解一般的均匀随机3-SAT问题实例难。
5 结论 本文考虑了一种严格随机正则(3, s)-SAT问题，并给出了该问题的实例产生模型--SRR模型。
1)证明了严格随机正则(3, s)-SAT问题可满足临界点的上界，即当变元规模N较大且s>11时，严格随机正则(3, s)-SAT公式是高概率不可满足的。
2)实验结果表明，SRR模型所产生的严格随机正则(3, s)-SAT问题实例的相变点位于s=11处。
3)严格随机正则(3, s)-SAT实例在相变点s=11处，比在相变点α?4.267处同规模的均匀随机3-SAT实例更难于求解。
4)本文所提出的严格随机正则(3, s)-SAT实例产生模型可以很方便地构造在相变点s=11处的随机3-SAT难解实例，这将有助于人们进一步理解3-SAT问题的难解本质，激发人们针对难解问题设计更好的求解算法。

参考文献

[1]	COOK S A.The complexity of theorem-proving procedures[C]//Proceedings of the 3rd Annual ACM Symposium on Theory of Computing.New York:ACM, 1971:151-158.
[2]	JOHNSON D S. The NP-completeness column:An ongoing guide[J].Journal of Algorithms, 1984, 5(3): 433–447.DOI:10.1016/0196-6774(84)90022-1
[3]	COOK S A, MITCHELL D G.Finding hard instances of the satisfiability problem:A survey[C]//Satisfiability Problem:Theory and Applications, DIMACS Series in Discrete Mathematics and Theoretical Computer Science.Piscataway, NJ:American Mathematical Society, 1997:1-17.
[4]	FRIEDGUT E, BOURGAIN J. Sharp thresholds of graph properties, and the k-SAT problem[J].Journal of the American Mathematical Society, 1999, 12(4): 1017–1054.DOI:10.1090/S0894-0347-99-00305-7
[5]	ACHLIOPTAS D, RICCI-TERSENGHI F.On the solution-space geometry of random constraint satisfaction problems[C]//Proceedings of the 38th Annual ACM Symposium on Theory of Computing.New York:ACM, 2006:130-139.
[6]	SEMERJIAN G. On the freezing of variables in random constraint satisfaction problems[J].Journal of Statistical Physics, 2008, 130(2): 251–293.
[7]	ACHLIOPTAS D, RICCI-TERSENGHI F. Random formulas have frozen variables[J].SIAM Journal on Computing, 2009, 39(1): 260–280.DOI:10.1137/070680382
[8]	MéZARD M, PARISI G, ZECCHINA R. Analytic and algorithmic solution of random satisfiability problems[J].Science, 2002, 297(5582): 812–815.DOI:10.1126/science.1073287
[9]	MéZARD M, ZECCHINA R. Random k-satisfiability problem:From an analytic solution to an efficient algorithm[J].Physical Review E, 2002, 66(5): 056126.DOI:10.1103/PhysRevE.66.056126
[10]	CHVáTAL V, REED B.Mick gets some (the odds are on his side)[satisfiability] [C]//Proceedings of 33rd Annual Symposium on Foundations of Computer Science.Piscataway, NJ:IEEE Press, 1992:620-627.
[11]	COJA-OGLAN A, PANAGIOTOU K.Catching the k-NAESAT threshold[C]//Proceedings of the 44th Annual ACM Symposium on Theory of computing.New York:ACM, 2012:899-908.
[12]	BOUFKHAD Y, DUBOIS O, INTERIAN Y, et al. Regular random k-SAT:Properties of balanced formulas[J].Journal of Automated Reasoning, 2005, 35(1): 181–200.
[13]	DING J, SLY A, SUN N.Satisfiability threshold for random regular NAE-SAT[C]//Proceedings of the 46th Annual ACM Symposium on Theory of Computing.New York:ACM, 2014:814-822.
[14]	RICCI-TERSENGHI F, WEIGT M, ZECCHINA R. Simplest random k-satisfiability problem[J].Physical Review E, 2001, 63(2): 026702.DOI:10.1103/PhysRevE.63.026702
[15]	MERTENS S, MéZARD M, ZECCHINA R. Threshold values of random k-SAT from the cavity method[J].Random Structures & Algorithms, 2006, 28(3): 340–373.
[16]	COJA-OGHLAN A.The asymptotic k-SAT threshold[C]//Proceedings of the 46th Annual ACM Symposium on Theory of Computing.New York:ACM, 2014:804-813.
[17]	DING J, SLY A, SUN N.Proof of the satisfiability conjecture for large k[C]//Proceedings of the 47th Annual ACM on Symposium on Theory of Computing.New York:ACM, 2015:59-68.
[18]	HAJIAGHAYI M T, SORKIN G B.The satisfiability threshold of random 3-SAT is at least 3.52[EB/OL].Ithaca, New York:Cornell University Library, 2003(2003-10-22)[2015-12-24].http://arxiv.org/abs/math/0310193v2.
[19]	KAPORIS A C, KIROUSIS L M, LALAS E G. The probabilistic analysis of a greedy satisfiability algorithm[J].Random Structures & Algorithms, 2006, 28(4): 444–480.
[20]	IMPAGLIAZZO R, LEVIN L A, LUBY M.Pseudo-random generation from one-way functions[C]//Proceedings of the 21st Annual ACM Symposium on Theory of Computing.New York:ACM, 1989:12-24.
[21]	XU K, LI W. Exact phase transitions in random constraint satisfaction problems[J].Journal of Artificial Intelligence Research, 2000, 12(1): 93–103.
[22]	XU K, LI W. Many hard examples in exact phase transitions[J].Theoretical Computer Science, 2006, 355(3): 291–302.DOI:10.1016/j.tcs.2006.01.001
[23]	XU K, BOUSSEMART F, HEMERY F, et al. Random constraint satisfaction:Easy generation of hard (satisfiable) instances[J].Artificial Intelligence, 2007, 171(8): 514–534.
[24]	TOVEY C A. A simplified NP-complete satisfiability problem[J].Discrete Applied Mathematics, 1984, 8(1): 85–89.DOI:10.1016/0166-218X(84)90081-7
[25]	DUBOIS O. On the r, s-SAT satisfiability problem and a conjecture of Tovey[J].Discrete Applied Mathematics, 1990, 26(1): 51–60.DOI:10.1016/0166-218X(90)90020-D
[26]	许道云. 极小不可满足公式在多项式归约中的应用[J].软件学报, 2006, 17(5): 1204–1212.XU D Y. Applications of minimal unsatisfiable formulas to polynomially reduction for formulas[J].Journal of Software, 2006, 17(5): 1204–1212.DOI:10.1360/jos171204(in Chinese)
[27]	RATHI V, AURELL E, RASMUSSEN L, et al.Bounds on threshold of regular random k-SAT[C]//13th International Conference on Theory and Applications of Satisfiability Testing.Berlin:Springer, 2010:264-277.
[28]	CASTELLANA M, ZDEBOROVá L. Adversarial satisfiability problem[J].Journal of Statistical Mechanics:Theory and Experiment, 2011, 2011(3): P03023.
[29]	SUMEDHA S, KRISHNAMURTHY S, SAHOO S. Balanced K-satisfiability and biased random K-satisfiability on trees[J].Physical Review E, 2013, 87(4): 042130.DOI:10.1103/PhysRevE.87.042130
[30]	KRISHNAMURTHY S. Exact satisfiability threshold for k-satisfiability problems on a Bethe lattice[J].Physical Review E, 2015, 92(4): 042144.DOI:10.1103/PhysRevE.92.042144
[31]	BAPST V, COJA-OGHLAN A.The condensation phase transition in the regular k-SAT model[EB/OL].Ithaca, New York:Cornell University Library, 2015(2015-10-07)[2015-12-24].http://arxiv.org/pdf/1507.03512v3.
[32]	KSCHISCHANG F R, FREY B J, LOELIGER H A. Factor graphs and the sum-product algorithm[J].IEEE Transactions on Information Theory, 2001, 47(2): 498–519.DOI:10.1109/18.910572
[33]	KIRKPATRICK S, SELMAN B. Critical behavior in the satisfiability of random Boolean expressions[J].Science, 1994, 264(5163): 1297–1301.DOI:10.1126/science.264.5163.1297
[34]	FLAJOLET P, SEDGEWICK R. Analytic combinatorics[M].Oxford: Cambridge University Press, 2009.
[35]	ROBBINS H. A remark on Stirling's formula[J].The American Mathematical Monthly, 1955, 62(1): 26–29.DOI:10.2307/2308012
[36]	CHVáTAL V, SZEMERéDI E. Many hard examples for resolution[J].Journal of the ACM, 1988, 35(4): 759–768.DOI:10.1145/48014.48016
[37]	DAVIS M, LOGEMANN G, LOVELAND D. A machine program for theorem-proving[J].Communications of the ACM, 1962, 5(7): 394–397.DOI:10.1145/368273.368557
[38]	MOSKEWICZ M W, MADIGAN C F, ZHAO Y, et al.Chaff:Engineering an efficient SAT solver[C]//Proceedings of the 38th Annual Design Automation Conference.New York:ACM, 2001:530-535.