即便采用传统的加速寿命试验方法,对于弹用电磁继电器这类长寿命高可靠的电子产品来说,也可能较少出现失效,甚至零失效,因此,很难利用失效数据在短期内对其贮存寿命进行评估[3]。而近年出现的基于退化参数数据的加速试验方法,相对于传统的加速寿命试验方法具有试验时间短、可靠性信息量大等优点,并得到了广泛的应用[4]。目前,针对工作条件下动态接触失效机理[5-7]、电弧侵蚀[8]、触点材料的接触特性研究,以及直流触点分断过程中的动熔焊、接触材料质量转移等方面的研究很多[9],但继电器贮存接触失效等方面的研究开展的并不多。有****对长期贮存后电磁继电器触点间的膜状腐蚀产物进行了化学、物理等特性分析,指出继电器触点间的腐蚀膜是由触点近表面区域或接触区域内部的扩散作用产生的[10-11], 文献[12]对电磁继电器的触点腐蚀膜进行了分析,并指出真空胶、松香与ZnCl2是导致触点表面腐蚀膜增长的关键因素。
分析继电器接触失效机理的通常做法一般只测量接触电阻,并在触点失效后借助光学显微镜、扫描电子显微镜(SEM)等设备对触点表面进行理化分析[13],该方法优点是可以用直观的方法全面地获取触点失效信息,但缺点是对于弹用电磁继电器这类密封产品来说,进行开壳观测费时、费力,甚至有时根本无法操作。动态接触电阻测量的触点失效方法实现了继电器触点失效的在线监测和预测[14], 但在不同继电器类型间的通用性方面尚存不足。对触点的腐蚀量进行数学建模也是进行接触失效分析的一种方法[15],但由触点侵蚀机理本身的复杂性,并且触点所处环境应力条件、触点材料等诸多因素影响,很难建立通用的数学模型。
研发了弹用电磁继电器的加速贮存退化试验综合分析系统,可同时对多达40支的弹用电磁继电器开展加速退化贮存试验。在贮存退化试验中除对接触电阻进行监测之外,还可对继电器的时间参数同时进行自动化检测。并以降低预测参数中随机信号对精度的影响为出发点,提出了时间序列与一维小波变换相结合的继电器贮存预测参数预处理方法,通过回归理论对贮存退化模型的参数进行了估计,最后,用所建模型对弹用电磁继电器正常温度应力下的贮存寿命进行了预测。
1 触点的接触退化机理 本文以某型转换型触点弹用电磁继电器为例,其结构示意图如图 1所示,为2组转换型电磁继电器,每组3个触点,分别是1个动触点(转换触点)和2个静触点(动合静触点和静合静触点)。具体动作过程可分为吸合和释放2个过程,继电器线圈通电时,衔铁在电磁吸力的作用运动,带动推动器并触动动簧片运动,动触点与动合静触点闭合,完成吸合过程。释放过程为:继电器线圈断电时,在机械反力(返簧系统与接触系统提供)作用下,动触点和动合静触点断开,并与静合静触点重新闭合。
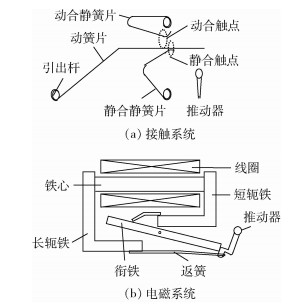 |
| 图 1 某型弹用电磁继电器结构示意图 Fig. 1 Structure schematic of missile electromagnetic relay |
| 图选项 |
弹用电磁继电器贮存期长,贮存过程中环境应力复杂,在长期温度、湿度、振动、腐蚀等环境因素综合作用下,会引起继电器相关特性参数的退化,直至失效。弹用电磁继电器结构紧凑,装配复杂,各零件尺寸很小,加工、装配的分散性大,产品的一致性不高,因此在长期贮存中失效模式与失效机理多样,且性能退化的随机性也较强。Takano和Mano[16]给出了触点的细微接触模型,具体研究了金属触点间腐蚀膜增长的数学模型建立方法。
金属表面腐蚀膜的生成与近表面区域或表面接触区域内部的扩散作用有关[16],具体过程如图 2所示,触点间真正接触的斑点周围形成了腐蚀环或氧化环。斑点处的离子被氧化,阴离子(O2-、Cl-和S2-等)通过氧化膜,由环的外部逐渐扩散到环的内部,而表面腐蚀膜的增长,发生在金属与腐蚀层的内部,当氧化反应与扩散作用同时发生时,接触区的表面腐蚀膜会发生向心式的增长,直到整个接触区域均被表面腐蚀膜覆盖。
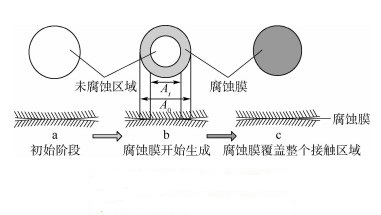 |
| A0-初始时刻的导电斑点平均直径;At-t时刻时导电斑点的平均直径。 图 2 触点间表面腐蚀膜向心渗入示意图 Fig. 2 Schematic of ingress inward of surface corrosion film in static contact |
| 图选项 |
图 3为某弹用电磁继电器静合触点长期贮存过程中,腐蚀前后的形貌对比图。
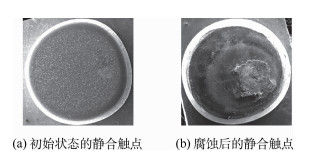 |
| 图 3 继电器静合触点形貌 Fig. 3 Normal closed static contact morphology of relay |
| 图选项 |
2 贮存退化试验 恒定应力加速退化试验的基本原理是将同一批次、一定数量的试品分成若干组,分别在某一恒定应力水平下进行加速性能试验,产品特性参数的退化量与施加应力的大小相关,应力越大的性能退化相对明显,然后可根据加速退化试验的性能退化轨迹外推出产品在正常应力下的寿命。
弹用电磁继电器体积小、组成零件复杂,并且在长贮期间会受到很多环境因素的影响,因此失效机理也较为复杂。在衡量电磁继电器的工作可靠性方面,振动是很关键的环境因素,但在继电器的整个贮存剖面中,振动对继电器贮存可靠性影响很小,可以忽略不计。通过前期摸底试验,湿度因素主要会导致绝缘电阻下降,但由于本文研究对象为密封结构,湿度也很难对继电器接触电阻产生较大影响。试验中施加综合应力比施加单一应力更能真实地模拟实际的贮存环境,暴露产品更多的缺陷,但同时也大幅提高了试验过程的复杂性,带来更多的随机干扰因素,最终可能会使得试验数据无法处理,而达不到试验最初预计的目的。文献[3]中指出,温度因素是影响继电器失效的主要环境因素。温度升高会加速继电器触点、簧片等部件发生物理、化学变化的过程,从而加速其失效过程。因此本文在探索研究阶段首先选取温度作为退化试验的加速应力,采用恒定应力加速退化贮存试验的方法对弹用电磁继电器进行贮存可靠性研究。贮存试验具有退化慢、耗时长的特点,本文拟将40支弹用电磁继电器空载,并平均分为4组分别置于4个温度箱中进行试验,定时对继电器的性能退化参数进行检测分析。
弹用电磁继电器贮存性能退化参数应能反应其贮存寿命与可靠性变化过程且应有明确的物理意义,并应易于测量。加速贮存试验的时间越长,退化趋势也应该越明显。贮存退化试验中除对接触电阻进行监测外,还对继电器时间参数(吸合时间、释放时间和回跳时间等)进行检测和分析,以获得更加丰富的触点退化状态可靠性信息。
在某一应力水平条件下,弹用电磁继电器失效具有随机性且应服从某种分布,因此在确定贮存退化应力水平时,应满足同分布且失效机理相同这一前提假设。并且由于通常在试验前加速系数未知,应力水平个数不宜太小或太大,但不应少于4个。
最大、最小环境应力间要有较大的间隔,最低应力应接近正常额定应力水平的加速额定值,但又不能与正常贮存条件过于接近,从而影响试验的加速性。本文所研究的某型转换型弹用电磁继电器的工作温度范围为-55~+125℃,考虑到其贮存环境的复杂多样(如移动阵地中,沙漠大气暴晒条件下环境温度可到70℃左右),并尽可能加快试验进程,拟将最低环境应力确定为80℃。弹用电磁继电器的结构复杂,构成材料品种繁多,其中绝缘垫片及线圈漆包线等相关构成部件的耐热等级如表 1所示。最高环境应力的选取要充分考虑试品材料、工艺、结构所能承受的应力设计极限,在保证失效机理一致的前提条件下,应尽可能提高最高应力水平。综合考虑其构成材料的耐温能力以及退化试验的加速性,并通过前期摸底试验在180℃以下,一般不出现绝缘失效,失效模式均为接触失效,以及考虑其他随机因素可能带来的温度波动,留出一定的温度应力余量,将最高试验温度应力确定为170℃。
表 1 弹用电磁继电器相关部件耐热等级 Table 1 Heat-resistant levels of relevant components for missile EMR
| 部件名称 | 构成材料 | 耐热等级 |
| 底板绝缘垫片 | 6050聚酰亚胺薄膜 | H级(180℃) |
| 润滑垫片 | 6050聚酰亚胺薄膜 | H级(180℃) |
| 线圈挡板 | 聚四氟乙烯棒 | C级(220℃) |
| 线圈组漆包线 | 改良聚酯亚胺漆包线(E180) | H级(180℃) |
| 线圈组漆包线 | 聚酰亚胺漆包线(QY-1) | C级(220℃) |
表选项
为了使中间各应力尽量分散。中间应力按倒数等间隔选取,具体计算公式为
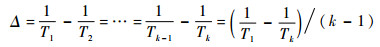 | (1) |
式中:Δ为温度应力间隔;Tk为第k个应力的温度。k值取4时,可确定加速应力从低到高依次为80、106、135和170℃。退化试验的具体条件见表 2。
表 2 加速退化试验条件 Table 2 Conditions of accelerated degradation test
| 参数 | 数值 |
| 试验温度应力/℃ | 80,106,135,170 |
| 试样数量 | 每个温度取10支 |
| 测试频率/d | 2 |
| 负载电流/mA | 10(防止产生电弧破坏触点形貌) |
| 其他要求 | 冷却至室温后再进行参数测试 |
表选项
弹用电磁继电器贮存退化试验综合测试系统整体结构与照片如图 4所示。
 |
| 图 4 弹用电磁继电器贮存退化试验系统整体结构及照片 Fig. 4 Major structure and photo of storage degradation testing system for missile EMR |
| 图选项 |
该测试系统可对多个温度应力下的多支弹用电磁继电器的时间参数及接触电阻进行轮流检测,并对试验数据进行分析处理。
3 试验结果分析 图 5为全部样品在一年贮存试验中4个温度下的接触电阻退化量平均值对比图。
 |
| 图 5 不同温度下接触电阻退化量平均值的对比图 Fig. 5 Comparison diagram of average degradation contact resistances at different temperatures |
| 图选项 |
图 6为4个温度下贮存退化试验中接触电阻实测值的散点连线图。通过图 6可分析出接触电阻在上述各温度应力下都存在较为明显的上升趋势。接触电阻平均值从初始的8 mΩ逐渐上升到12 mΩ左右。还可看出,温度对接触电阻的退化起到了促进作用,温度越高,接触电阻增长速度越快,且值也越大。
 |
| 图 6 不同温度下接触电阻实测值的散点连线图 Fig. 6 Scatter plots of real test data for contact resistances at different temperatures |
| 图选项 |
贮存试验中接触电阻的逐渐变大也体现了继电器触点在贮存期内的累积退化状况,触头表面逐渐出现氧化腐蚀物的堆积。温度与触头表面的腐蚀膜扩散增长速度正相关,也验证了温度是影响其贮存可靠性的最主要环境因素,环境温度越高,氧化腐蚀物的增长速度越快。从而接触电阻在不同温度应力下表现出不同的增长趋势。
4 贮存回归退化模型及寿命预测 在继电器长贮期间,其主要的失效形式是触点的接触退化失效,因此弹用电磁继电器的贮存退化过程,可以通过敏感退化参数的变化来表征。
4.1 贮存退化敏感参数预处理 弹用电磁继电器贮存环境复杂,其贮存失效过程也存在干扰等随机因素,且试验测试仪器也存在测量误差,因此通过贮存退化试验得到的监测数据通常包含噪声与干扰信号。为了预测得到较高精度的贮存寿命,对试验所测数据进行预处理,减少干扰和噪声带来的误差就显得尤为重要。目前常见的试验数据预处理方法主要有异常值剔除、趋势项提取及均值归一化处理、信号变换等。
弹用电磁继电器的退化贮存试验中得到的监测参数视为一非平稳时间序列。作为贮存敏感退化参数之一的接触电阻也由随机项与趋势项2种时间序列叠加而成。
随机项体现贮存中接触电阻的随机性,可看作平稳零均值时间序列。趋势项则体现弹用电磁继电器贮存过程中接触电阻的整体退化趋势,是建立贮存退化模型的关键。拟通过时间序列分析与一维小波变换相结合的方法对试验敏感退化参数进行分解和重构,使得趋势项得以保留,随机成分得以去除,从而建立弹用电磁继电器的贮存退化回归模型,完成贮存寿命的预测和评估。
4.1.1 一维小波变换 一维小波变换的实质是通过某种基函数(分析宽度逐渐变化)对信号进行分析,来实现不同频率范围中具有不同分辨率的功能。一维小波变换的过程可分为小波分解和小波重构。根据多分辨率理论和滤波器组原理,一维小波分解是指把原始信号M通过一个由高通滤波器和低通滤波器组组成的二维滤波器组,分别提取出高频细节信号和低频尺度信号。低频尺度信号再通过一个双通道滤波器组做进一步的分解,不断循环这个过程直到对低频尺度信号分解到第n层。然后对最终分解获得的信号进行小波重构,则原始信号可最终表示为
 | (2) |
式中:Ln为第n层低频尺度信号重构结果;Hk为第k层高频细节信号重构结果,k=1, 2, …,n。
在弹用电磁继电器贮存退化敏感参数的时间序列分析中,低频尺度信号的重构结果Ln作为趋势项,体现了原始信号M的整体变化趋势;高频细节信号的重构结果H1+H2+…+Hn作为随机项,体现了原始信号M中的受干扰情况。
4.1.2 时间序列分析 时间序列是随机过程的一种特殊存在形式,可看作一个随机过程产生的结果。此处把随机项作为时间序列进行分析,把高频细节成分视为干扰部分,则一定要对其进行平稳性和零均值检验,来确保随机项中不存在任何趋势项信息。
对于平稳性检验,目前的检验方法有参数法、偏相关法、自相关法和单位根法等众多检验方法。本文选用单位根法,该方法相对客观,其基本流程包含:①建立时间序列模型;②对该模型特征参数构成的特征方程和特征根进行求解;③以特征根是否在单位圆内来对其平稳性进行检验(全部特征根λ < 1,即单位圆内,则可判断该序列为非平稳)。此方法多用于自回归滑动平均(ARMA)模型来表示平稳时间序列。
而对于零均值检验,实质就是对原始序列的均值μ是否为0进行假设检验,即原假设H0:μ=0。定义统计变量为
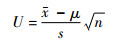 | (3) |
式中:x为序列样本均值;s为序列样本标准方差;n为序列样本长度。
由中心极限定理与大数定率可知,当原假设H0为真时,U应该服从标准正态分布。对于置信水平α(α取0.05),可通过查表得到临界值μα/2。若|x-μ|≤μα/2,则接受序列为零均值的假设H0,否则拒绝原假设H0。
4.1.3 时间序列的趋势项提取算法 首先对弹用电磁继电器贮存退化试验得到的原始试验数据进行野值剔除,得到参数Mr(接触电阻、时间参数等贮存退化敏感参数),趋势项提取的最终目的是保证既不损失趋势信息,又实现了其中随机成分的最大去除。本文用n层一维小波变换对Mr进行分解,利用高频细节信号与低频尺度信号的平均值检验确定小波的层数,确定n值。具体退化试验敏感参数的趋势项提取预处理算法流程如图 7所示,图中:Y为线性回归方程的一般化形式表达式。
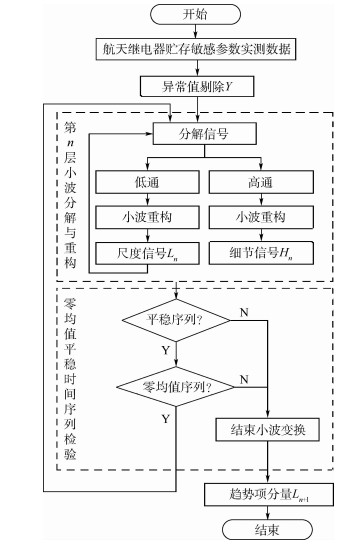 |
| 图 7 趋势项提取的算法流程图 Fig. 7 Flowchart of trend extraction algorithm |
| 图选项 |
对Mr进行第1层小波分解,得到高频细节信号与低频尺度信号,对高频细节信号进行平稳零均值检验,若该高频细节信号通过检验,则继续对低频尺度信号进行第2层小波分解,据此类推,直到高频细节信号不满足平稳零均值检验,把此时的小波分解层数记做n,则第n-1次小波分解所获得的低频尺度信号就是最终要提取的趋势项信息。
4.2 回归预测方程与参数估计 通常回归方程包括非线性回归方程与线性回归方程,且非线性回归方程大都可由某种变换方式转换成线性回归方程的形式。因此本文主要关注线性回归方程的构建和方程的参数估计方法。
线性回归方程的一般化形式为
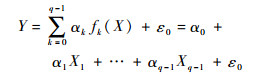 | (4) |
式中:fk(X)为k个线性无关的确定函数,X为测试k次的函数,k=0, 1, …, q-1;Xq-1为第q-1次测试值的趋势项大小;αk为回归参数;ε0为随机误差,假设有∑ε0=0。
由此可见,线性回归方程只要满足回归方程的参数αk与Y满足线性关系即可,并不要求Y与X必须为线性。
可用继电器贮存退化试验得到的监测参数实测数据对线性回归方程进行参数估计。若贮存试验中共进行了k次检测,第q次的退化敏感参数趋势项的值为yk,则满足:
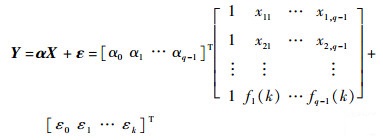 | (5) |
式中:fk(X)构成矩阵;Y为k次敏感退化参数之实测值趋势项;α为待估计回归参数;ε为随机测试误差量,设满足标准正态分布。
可由最小二乘法求出α和ε的估计值α′和ε′:
 | (6) |
式中:
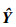
再将估计值α′代入式(4),可得到所构建的回归退化方程如下:
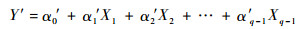 | (7) |
式中:Y′为实测值Y的估计值(预测值)。
由退化试验果分析可知,随着贮存时间的延长,弹用电磁继电器的贮存敏感退化参数的退化趋势呈现递增或递减的规律,而回归方程的结构形式影响着最终的预测精度,因此第1步应确定回归模型的结构形式,第2步再进行回归预测方程的参数估计。拟把表 3中的几种回归模型作为最优回归预测方程的备选库。
表 3 最优回归贮存退化模型函数备选库 Table 3 Alternative function library of the best storage regress degradation model
| 初始回归函数形式 | 变换过程 | 变换后的 线性回归方程 |
线性函数: 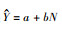 |  | Y=α0+α1X1 |
指数函数:  |  | Y=α0+α1X1 |
幂函数: 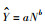 | 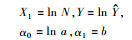 | Y=α0+α1X1 |
表选项
如式(8)所示,一般由残差平方和法(SSE)来评价实测数据回归退化模型的拟合优度。
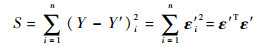 | (8) |
式中:S为残差平方合法拟合优度值。SSE法中,S的值越小说明回归函数的拟合值与实测值偏差越小,拟合效果越好。因此各回归函数中,S值最小的函数即为最优回归函数。
4.3 贮存寿命预测及评价 建立弹用电磁继电器的贮存退化回归模型,主要是通过模型曲线的外推,在其失效前,对弹用电磁继电器的贮存寿命进行预测。也为比较分析其在不同环境应力下的退化过程提供了技术方法。
当弹用电磁继电器的贮存退化预测参数值达到失效阈值D,则可认定其贮存失效,此时对应的时间即为弹用电磁继电器贮存寿命的预测值。通过贮存退化方程式(7)及表 3中的回归函数变换形式,将失效阈值D作为预测值Y′,得
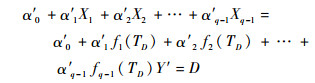 | (9) |
式中:TD为继电器的贮存寿命预测值。
求解式(9)就可以得出弹用电磁继电器贮存寿命的预测值TD,该值可视为其真实贮存寿命的一个点估计值。一般工程应用中,除对TD进行点估计之外,还需进行区间估计。区间估计也可间接评价点估计的精度和可靠度,其中置信区间用来刻画估计精度,显著性水平用来刻画可靠性。
对于线性回归模型,预测值具有如下性质:
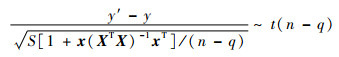 | (10) |
式中:x为时间数据;y为实测值;y′为y的估计值;t(n-q)为变量t服从自由度为n-q的t分布。
对于显著性水平α(α取0.05),由式(10)可知,Y在x=[1, x1, …, xq-1]处的值y的置信区间为
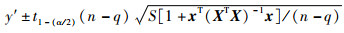
 | (11) |
式中:xX为TDX由表 3变换后得到的向量解;xS为TDS由表 3变换后得到的向量解。
最后用回归方程式(11)即可求得TDX与TDS的具体数值解。本文仅以弹用电磁继电器贮存敏感退化参数中的接触电阻为例,将接触电阻作为贮存寿命的预测变量,根据该型弹用电磁继电器产品手册[17]中的规定,接触电阻的贮存失效阈值设为50 mΩ。
选择试验中4个温度应力的继电器实测数据,首先用4.1.1节中数据预处理方法进行一维小波分解和重构,然后用时间序列方法得到的数据预处理结果, 如图 8所示,最后在利用表 3中所列的回归函数对趋势项进行依次拟合。
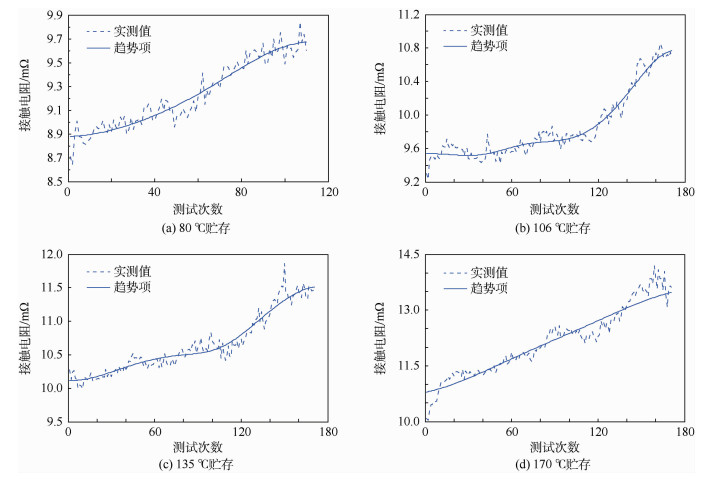 |
| 图 8 不同温度应力下接触电阻的预处理结果 Fig. 8 Results of pretreatment for contact resistances with different temperature stresses |
| 图选项 |
根据残差平方和法中S最小原则,可确定弹用电磁继电器接触电阻的最优贮存回归退化预测模型的函数结构形式为指数函数。贮存寿命预测结果(伪贮存寿命)的点估计及区间估计值如表 4所示。
表 4 贮存试验样品的最优回归退化模型及贮存寿命预测结果 Table 4 Best regress degradation model and storage life prediction results for storage test samples
| 温度/℃ | S值 | 最优回归 退化模型 | 预测参数 失效阈值D/mΩ | 预测寿命 点估计TD/d | 区间估计 (TDX, TDS)/d | ||
| 线性函数 | 指数函数 | 幂函数 | |||||
| 80 | 2.408 | 2.297 | 7.150 | 指数函数 | 50 | 6012 | (5746, 6548) |
| 106 | 0.315 | 0.259 | 4.677 | 指数函数 | 50 | 5424 | (5356, 5566) |
| 135 | 5.246 | 4.877 | 15.637 | 指数函数 | 50 | 4136 | (3988, 4550) |
| 170 | 0.219 | 0.099 | 21.712 | 指数函数 | 50 | 2234 | (2218, 2242) |
表选项
由于弹用电磁继电器属于长寿命高可靠机电元件,其贮存退化相当缓慢,在退化试验过程中,未有试样失效,即未获得其实际的贮存寿命,因此对各温度下贮存寿命的预测精度,只能采用区间估计的方式对其贮存寿命预测结果进行分析与评价。
弹用电磁继电器的贮存环境温度范围一般为25~32℃,即使野外露天库房贮存或阵地转运,环境温度通常也不会超过45℃。为了预测其实际贮存温度下的贮存寿命,可通过表 4中的4个预测寿命区间估计值及文献[18]中建立的弹用电磁继电器贮存退化物理方程联立求得。
文献[18]中已通过贮存失效机理分析,并得出其贮存失效物理方程符合Arrhenius模型的结构,即
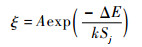 | (12) |
式中:ξ为应力Sj下的贮存寿命特征量,如平均寿命、中位寿命;A为常数;ΔE为失效机理激活能;k为玻尔兹曼常数;Sj为第j个开氏温度加速应力水平。
为了方便求解,可将式(12)两边取对数,将其进行线性化。
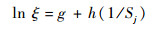 | (13) |
式中:g=lnA为待定参数;
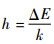
为求解待定参数g、h,可通过表 4中对应温度下的预测寿命值代入式(13)中求得。此处选择区间估计的下限值来求解方程待定参数的估计值
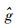

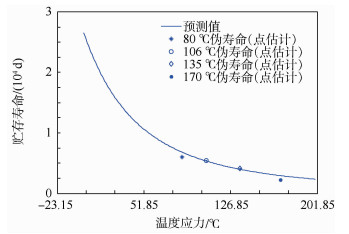 |
| 图 9 不同温度应力下弹用电磁继电器贮存寿命预测曲线 Fig. 9 Prediction curve of storage life for missile EMR with different temperature stresses |
| 图选项 |
取显著性水平α=0.05时,计算得出的正常温度应力下贮存寿命预测值如表 5所示。
表 5 弹用电磁继电器常温下的贮存寿命预测值 Table 5 Storage life prediction results of missile EMR in normal temperature stress levels
| 正常温度应力条件/℃ | 25 | 32 | 45 |
| 贮存寿命预测值/d | 16388 | 14531 | 11785 |
表选项
5 结论 1) ?提出了平稳时间序列和小波分析相结合的弹用电磁继电器贮存敏感参数预处理方法。通过趋势项提取预处理算法,将原始试验数据中的随机成分最大程度去除,以保证所建模型的预测精度。
2) ?建立了以弹用电磁继电器接触电阻为敏感退化参数的贮存回归预测方程,对正常温度应力下的贮存寿命进行了预测。通过线性回归分析法,对实测数据预处理后的趋势项数据进行了回归退化分析建模,确定指数形式为最优回归预测函数形式,并对其参数进行了估计。通过回归预测方程,对各温度应力下的伪贮存寿命进行了预测,并结合已建立的贮存失效物理方程对常温下的弹用电磁继电器贮存寿命进行了预测。
参考文献
| [1] | 郭凤仪, 陈中华. 电接触理论及其应用技术[M].北京: 中国电力出版社, 2008: 1-18.GUO F Y, CHEN Z H. Electrical contacts theory applications and technology[M].Beijing: China Electric Power Press, 2008: 1-18.(in Chinese) |
| [2] | 尚爱聪.军用密封继电器非工作状态贮存可靠性研究[C]//第八届全国可靠性物理学术讨论会论文集.北京:中国电子学会, 1999:263-270.SHANG A C.Military sealed relays non-work storage reliability research[C]//Proceedings of the 8th National Reliability Physical Seminar.Beijing:Chinese Institute of Electronics Press, 1999:263-270(in Chinese). |
| [3] | 陆俭国, 骆燕燕, 李文华, 等. 航天继电器贮存寿命试验及失效分析[J].电工技术学报, 2009, 24(2): 54–59.LU J G, LUO Y Y, LI W H, et al. Storage life test and failure analysis of aerospace relays[J].Transactions of China Electrotechnical Society, 2009, 24(2): 54–59.(in Chinese) |
| [4] | CHEN Z H, ZHENG S R. Lifetime distribution based degradation analysis[J].IEEE Transactions on Reliability, 2005, 54(1): 3–10.DOI:10.1109/TR.2004.837519 |
| [5] | NEUHAUS A R, RIEDER W F, HAMMERSCHMIDT M. Influence of electrical and mechanical parameters on contact welding in low power switches[J].IEEE Transactions on Components and Packaging Technologies, 2004, 27(1): 4–11.DOI:10.1109/TCAPT.2004.825777 |
| [6] | CHEN Z K, WITTER G.Dynamic welding of silver contacts under different mechanical bounce conditions[C]//Proceedings of the 45th IEEE Holm Conference on Electrical Contacts. Piscataway, NJ:IEEE Press, 1999:1-8. |
| [7] | MCRBRIDE J W, SHARKH S M. Electrical contact phenomena during impact[J].IEEE Transactions on Components Hybrids, Manufacture Technologies, 1992, 15(1): 184–192. |
| [8] | RIEDER W F, NEUHAUS A R. Short arc modes determining both contact welding and material transfer[J].IEEE Transactions on Components and Packaging Technologies, 2007, 30(1): 9–14.DOI:10.1109/TCAPT.2007.892056 |
| [9] | CHEN Z K, WITTER G.Comparison in performance for silver-tin-indium oxide materials made by internal oxidation and power metallurgy[C]//Proceedings of the 55th IEEE Holm Conference on Electrical Contacts.Piscataway, NJ:IEEE Press, 2009:180-186. |
| [10] | TAMAI T. Effect of humidity on growth of oxide film on surface of copper contacts[J].IEICE Transactions on Electron, 2007, E90-C(7): 1391–1397.DOI:10.1093/ietele/e90-c.7.1391 |
| [11] | READ M B, LANG J H, SLOCUM A H.Contact resistance in flat thin films[C]//Proceedings of the 55th IEEE Holm Conference on Electrical Contacts.Piscataway, NJ:IEEE Press, 2009:300-306. |
| [12] | 臧春艳, 何俊佳, 李劲, 等. 密封继电器接触电阻与表面膜研究[J].中国电机工程学报, 2008, 28(31): 125–130.ZANG C Y, HE J J, LI J, et al. Contact resistance and surface film of saealed relay contacts[J].Proceedings of the CSEE, 2008, 28(31): 125–130.(in Chinese) |
| [13] | 郭凤仪, 王国强, 董讷. 银基触头材料电弧侵蚀特性及裂纹形成机理分析[J].中国电机工程学报, 2004, 24(9): 209–217.GUO F Y, WANG G Q, DONG N. The arc erosion characteristics and crack formation mechanisms analysis of silver-based contact materials[J].Proceedings of the CSEE, 2004, 24(9): 209–217.(in Chinese) |
| [14] | 陈鹏, 陆俭国, 姚芳, 等. 动态接触电阻测量及触点失效预测研究[J].电工电能新技术, 2005, 27(3): 27–30.CHEN P, LU J G, YAO F, et al. Research on dynamic contact resistance measurement and failure prediction of relay contacts[J].Advanced Technology of Electrical Engineering and Energy, 2005, 27(3): 27–30.(in Chinese) |
| [15] | 吴细秀, 李震彪. 电器电极材料喷溅侵蚀的理论计算[J].中国电机工程学报, 2003, 23(6): 96–101.WU X X, LI Z B. Theoretic analysis on sputtering erosion of electrode[J].Proceedings of the CSEE, 2003, 23(6): 96–101.(in Chinese) |
| [16] | TAKANO E, MANO K. The failure mode and lifetime of static contacts[J].IEEE Transactions on Component, Packaging, and Manufacturing, 1968, 4(2): 51–55. |
| [17] | 张增照.电子设备非工作状态可靠性预计手册:GJB/Z 108A-2006[S].北京:总装备部军标出版发行部, 2007:52-54.ZHANG Z Z.Nonoperating reliability prediction handbook for electronic equipment:GJB/Z 108A-2006[S].Beijing:Department of General Equipment Department of Military Standard Publishing, 2007:52-54(in Chinese). |
| [18] | WANG Z B, ZHAI G F, HUANG X Y, et al.Study on feasibility of storage accelerated testing based on parameter degradation for aerospace relays[C]//Proceedings of the 3rd Annual IEEE Conference on Prognostics and System Health Management.Piscataway, NJ:IEEE Press, 2012:1-5. |
