在以往的研究中, 模型迁移理论主要应用在建立过程模型上[1-3], 它需要一个成熟的具有明确可信度的过程模型作为基模型, 当需要建立的新过程模型与基模型具有明确相似性时, 可以使用模型迁移方法基于基模型对新过程建模。根据高超声速相似律[4-5], 具有尖头薄体或尖头旋转体的高超声速飞行器, 当它们具有仿射相似构型时, 对应的气动参数间在特定的飞行环境下满足一定的线性关系[4-6]; 此时可以基于模型迁移方法对飞行器建模。
以薄体尖头飞行器为主要研究对象, 首先设计了一种评价飞行器气动外形间相似度的方法, 进而基于高超声速相似律使用模型迁移方法对高超声速飞行器建模。模型迁移方法需要一个成熟并且具有明确可信度的飞行器的气动参数模型作为基模型, 对应的飞行器作为基飞行器。当需要对一个与基飞行器具有一定相似度的飞行器进行建模时, 需要通过求解2个飞行器气动外形间的线性关系, 计算相似度。当2个飞行器的相似度满足一定指标时, 可以基于高超声速相似律迁移得到新飞行器的气动参数。为了评估迁移得到的气动参数的精度,本文使用CFD获取部分新飞行器的气动参数与前面迁移得到的气动参数对比, 当迁移得到气动参数精度满足建模要求时认为建模完成; 当不满足要求时使用已有的新飞行器的气动参数对迁移过程修正。利用气动参数随高度变化的规律计算整个空域的高超声速飞行器的气动参数。最后通过仿真验证了本文给出的建模方法的有效性。
1 飞行器仿射相似度评估 飞行器气动外形间相似度评估的目的是为了验证不同飞行器间是否可以使用模型迁移方法建模。本文用到的飞行器机体坐标系以飞行器头部顶点为坐标原点O, X轴在飞行器对称平面内平行于飞行器的设计轴线指向机尾, Z轴在飞行器对称平面内与X轴垂直并指向机体上方, Y轴可通过右手定则确定。假设具有完整的气动参数的飞行器为基飞行器,需要计算气动参数的飞行器为新飞行器。本文用LXb和LXn分别无量纲基飞行器X轴方向上和新飞行器X轴方向上变量,以Lb和Ln分别无量纲基飞行器和新飞行器Y轴和Z轴方向上的变量。
对于具有仿射相似性的2个飞行器, 将1个飞行器表面上任意一点通过统一的线性变换, 得到的点都可以在另外1个飞行器表面找到, 并且这种转换关系是可逆的, 即
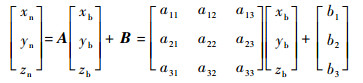 | (1) |
式中:Pb=[xb?yb?zb]T为基飞行器表面的点; Pn=[xn?yn?zn]T为对应的新飞行器表面的点; 矩阵A和B为需要求解的2个线性常量矩阵。由于高超声速飞行器都是面对称的流线体, 所以矩阵A应是一个满秩且主对角线按行占优阵。
由于飞行器都是面对称构型, 并且对称面对飞行器的气动特性影响很大, 所以这里先对2个飞行器对称平面进行线性拟合, 此时式(1)变为
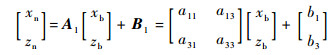 | (2) |
如图 1所示,在基飞行器X轴上均匀地取点, 经过这些点做平行于Z轴的直线交飞行器上下表面于2个点。当在X轴上选取n个点时, 得基飞行器表面2n个点。取无量纲的xn=xb时,可得a11=1, a13=b1=0, 可以得到新飞行器表面对应的2n个点。由这2n组对应点, 通过式(3)可以计算矩阵A1和B1中余下变量的最优解:
 |
| 图 1 基飞行器表面取点示意图 Fig. 1 Schematic diagram of selected points on surface of base vehicle |
| 图选项 |
 | (3) |
式中:
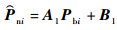
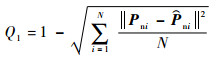 | (4) |
沿基飞行器X轴上的n个点做平行于Z轴的直线相交于飞行器表面成为n条线段。如图 1中飞行器尾部的线段所示, 对每个线段均匀选取n1个点, 并经过这些点做平行于Y轴的直线, 相交于飞行器Y轴正方向的表面得到nn1个点。同理可以得到新飞行器表面Y轴正方向对应的nn1个点。基于这nn1组点通过式(3)计算得到矩阵A与B中的余下变量的最优解。使用式(4)计算2个飞行器Y轴方向上的相似度Q2。
为了突出飞行器对称面的相似度对飞行器构型相似度的贡献度, 2个飞行器的相似度计算公式为
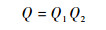 | (5) |
2 模型迁移 模型迁移的方法(PMBPS)是通过获取相似过程行为的共同点, 在已建立的模型基础上, 利用较少的实验数据建立和开发具有相似过程的新模型。由高超声速相似律可知:对于绕仿射相似的薄体高超声速流动, 当2个飞行器的γ、Ma∞、τ和α/τ分别相等时, 则它们的无因次解也相等[5, 7-8](γ为比热比, Ma∞为飞行器所处远场马赫数, τ为飞行器的相对厚度,α为攻角)。
由高超声速相似律, 可以得到本文给出的模型迁移建模方法适用于具有强仿射相似外形的高超声速飞行器。本文用到的模型迁移方法的基本流程如图 2所示。可以得到使用模型迁移方法要求:①有一个与新飞行器具有强仿射相似度的飞行器作为基飞行器; ②基飞行器的气动参数足够反应它的气动特性, 能支持新飞行器迁移建模; ③能够对新飞行器做少量的实验。
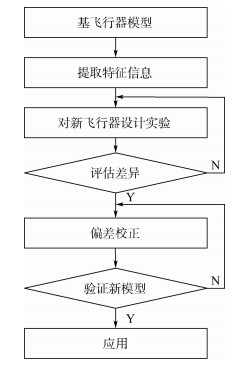 |
| 图 2 模型迁移流程 Fig. 2 Flowchart of model migration |
| 图选项 |
只有满足以上3个条件时才能够使用本文给出的建模方法迁移得到新飞行器的气动模型, 从而降低飞行器建模周期与实验成本。
2.1 提取特征信息 研究发现无黏流的条件下, 对于满足仿射相似理论的薄体飞行器的升力系数CL与τ2或α2成正比, 与马赫数的平方Ma2成反比; 阻力系数CD与τ3或α3成正比, 与Ma3成反比[9]。由于飞行器飞行过程中要求侧滑角保持在0°附近,可认为侧滑角β=0, 因此本文主要研究阻力系数和升力系数。
在无黏流的条件下, 由高超声速相似律可以得到2个飞行器的升力系数存在如下关系:
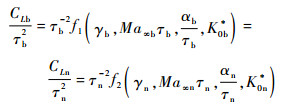 | (6) |
式中:带下标b和n的变量分别为基飞行器和新飞行器的对应变量;τ取对应飞行器迎风面的最大相对厚度τmax; K0*=R0CX0/(lτ3)为反映飞行器钝头影响的相似参数[10], R0为飞行器头部半径, CX0为头部引起的轴向力系数, l为飞行器长度。同理2个飞行器间的阻力系数存在式(7)的关系:
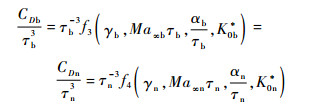 | (7) |
通过式(6)和式(7)可以迁移得到新飞行器的升力系数和阻力系数。
对于高超声速飞行器, 激波层与边界层的相互作用主要发生在大马赫数、小雷诺数的场合[11], 而高超声速飞行器正是主要处在这样的飞行环境中。在高超声速条件下, 当气流角一定时, 由黏性引起的压强系数Cp与雷诺数Re和马赫数Ma存在如式(8)的关系[12-14]。
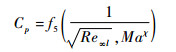 | (8) |
式中: χ会因边界层与激波作用强度不同而变化; Re∞l=ρ∞V∞l/μ∞, ρ∞、V∞和μ∞分别为自由流中气体的密度、速度和黏性系数。当马赫数与气流角确定时,
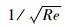
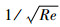
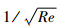
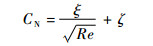 | (9) |
式中: CN为轴向力系数和法向力系数的任一量;ξ与ζ为常量。由于雷诺数与飞行器所处的高度存在对应关系, 所以可根据黏性力的这种特性计算不同高度上的气动参数。
2.2 设计实验 设计实验的目的是为了评估模型迁移结果的精度, 并支持部分迁移变量的计算。飞行器在不同飞行环境下所表现出来的气动性能具有很大不同, 所以在设计实验时应尽量体现出新飞行器所需的飞行环境的气动参数。
由于攻角与马赫数是式(6)和式(7)迁移用到的变量, 而高度对黏性力的影响很大且不能忽略, 所以使用式(6)和式(7)迁移时应在相同高度条件下。在相同高度下设计实验时只需体现出高度和气流角对气动参数的影响。为了迁移获得变量高度上的气动参数, 需要通过实验获得2个或更多高度下的气动参数来支持式(9)的计算。
2.3 评估差异 假设2个飞行器的比热比γ保持不变, 而飞行器间的头部半径影响可通过修正量修正; 由式(6)和式(7)可以得到2个具有薄体仿射相似构型的飞行器满足式(10)时, 飞行器间的气动参数满足线性关系。
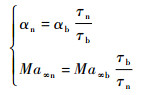 | (10) |
实验得到的新飞行器的气动参数Cn(Cn可以是升力系数和阻力系数的任一量), 在相同高度条件下通过式(10)查找对应基飞行器的气动参数Cb,则有
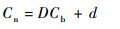 | (11) |
式中:D与d为常数。通过式(12)获得2个飞行器对应气动参数间的线性度R[1]
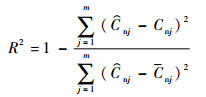 | (12) |
式中: Cn为这些气动参数的平均值;
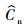
2.4 偏差校正 当具有复杂气动外形的2个高超声速飞行器满足高超声速相似律时, 依据高超声速相似律两者对应表面的压强系数依然满足比例关系, 所以当忽略摩擦阻力时, 2个飞行器的气动参数间依然存在比例关系[15-16]。但是当τ值不等于飞行器最大相对厚度, 即迁移用到的τ≤τmax; 此时需要重新计算τ, 相应地气动参数之间的比例关系需要重新修正。由于高超声速飞行器的激波层较薄, 这样使得边界层厚度与激波层相比不能略去, 甚至还会出现整个激波层都具有黏性的情况,所以高超声速飞行器所受的黏性效应是不能被忽略的, 此时2个飞行器气动参数间的关系式需要修正。
假设飞行器最小相对厚度设定为τmin, 定义K=τn/τb, 则有Kmin=τn?min/τb?max以及Kmax=τn?max/τb?min。在相同高度下新飞行器的升力系数与基飞行器的升力系数间存在:
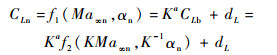 | (13) |
式(13)中存在3个未知量需要计算, 可以通过求解式(14)获得K、a与dL的最优解:
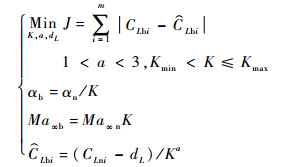 | (14) |
在相同高度下, 新飞行器的阻力系数与基飞行器的阻力系数间存在如下关系:
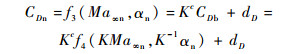 | (15) |
式(15)中有2个未知量需要计算,可以通过求解式(16)获得c与dD的最优解:
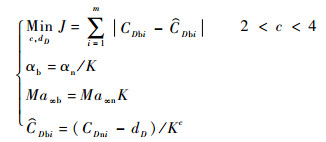 | (16) |
飞行器气动参数随高度的变化可以通过线性拟合获得, 即已知新飞行器2个或以上高度下的气动参数时, 在相同马赫数和攻角条件下, 利用式(9)可以计算得到新飞行器的气动参数在其他高度的值。当迁移完成时, 可以利用实验获得的新飞行器气动参数的真实值与迁移值对比, 评估迁移误差。
3 仿真 为了验证本文给出的建模方法的正确性, 本文使用文献[17]中给出的2种高超声速飞行器(如图 3和图 4所示)进行迁移仿真验证。使用CFD可以得到基飞行器的气动参数, 使其能满足迁移新飞行器气动参数所需要的条件, 并且可以对新飞行器迁移过程中需要的气动参数进行计算。
 |
| 图 3 基飞行器 Fig. 3 Base vehicle |
| 图选项 |
 |
| 图 4 新飞行器 Fig. 4 New vehicle |
| 图选项 |
计算2个飞行器的仿射相似度, 设定2个飞行器的相似度Q>0.8时,2个飞行器可以使用本文给出的建模方法, 当2个飞行器的Ma≥8时飞行器外流场达到高超声速流。并且2个飞行器的参考面积都取其在攻角为零时机体在水平面的投影面积。
由于飞行器迎风面对整个飞行器的气动特性影响很大, 所以本文定义的LXb如图 5所示。为了保证新飞行器机尾处无量纲值与基飞行器相同, 可以计算得到LXn=lnLXb/lb, 其中ln与lb分别为新飞行器和基飞行器机体长度。Lb和Ln分别选择对应飞行器机体的高度。分析图 3和图 4可得2个飞行器的相似度可以通过评估2个飞行器上表面Y轴正方向的相似度得到。
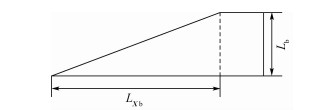 |
| 图 5 基飞行器侧视图 Fig. 5 Side view of base vehicle |
| 图选项 |
在基飞行器X轴上均匀的选取20个点, 使用本文给出取点方式可以得到飞行器上表面20组点, 此时可以通过式(2)和式(3)计算得到矩阵A1和B1:
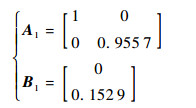 | (17) |
通过式(4)计算得到2个面的相似度Q1=0.8909。
取n1=12, 则可以得到飞行器表面Y轴正方向上240组点。通过式(3)可以得到矩阵A与B:
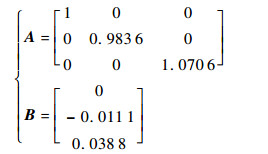 | (18) |
计算可以得到飞行器Y轴方向的相似度Q2=0.9209。此时可以计算得到2个飞行器的相似度Q=Q1Q2=0.8204。由于Q>0.8, 所以2个飞行器可以进行模型迁移。由于2个飞行器的相似度不等于1, 这样会对新飞行器的建模精度产生一定的影响。
通过测量2个飞行器的外形, 可以得到基飞行器的τb?max=0.8333, 新飞行器的τn?max=1.2500。本文选取飞行器机体高度和长度的比值为最小相对厚度τb?min=τn?min=0.6667, 可以得到Kmax=1.8750、Kmin=0.8000。使用式(6)和式(7)可以迁移得到新飞行器高超声速流下的气动参数。
Ma=13、h=40 km时的升力系数和阻力系数随攻角变化的曲线如图 6所示。此时新飞行器的气动参数是由基飞行器Ma=19.5时迁移得到的, 由于基飞行器的气动参数是考虑高超声速粘性效应的, 使得无黏流假设下得到的式(6)和式(7)迁移得到的新飞行器的气动参数产生较大误差, 所以需要对迁移过程进行偏差修正。
 |
| 图 6 实验和模型迁移得到的新飞行器升力系数与阻力系数随攻角变化的曲线 Fig. 6 Curves of lift coefficient and drag coefficient of new vehicle from experiment and model migration changing with attack angle |
| 图选项 |
本文选取的对新飞行器的特征实验点及其气动参数如表 1所示。使用表 1中的气动参数通过式(13)、式(14)可以得到K=1.4950、a=1.7340、dL=0.0704。迁移可以得到新飞行器的在40 km处的升力系数。马赫数为13、高度h为40 km处的升力系数如图 7(a)所示。此时迁移用到的是基飞行器Ma=19.4356时的气动参数迁移得到的。由于迁移公式得到了修正,使迁移精度进一步提高到在α < 18°时最大误差控制2%以内。
表 1 新飞行器的实验数据 Table 1 Experiment data of new vehicle
| 编号 | α/(°) | Ma | h/km | CDn | CLn |
| 1 | 0 | 10 | 40 | 0.107 9 | -0.2170 |
| 2 | 7 | 10 | 40 | 0.1336 | 0.4424 |
| 3 | 14 | 10 | 40 | 0.4410 | 1.4230 |
| 4 | 0 | 12 | 40 | 0.1015 | -0.2195 |
表选项
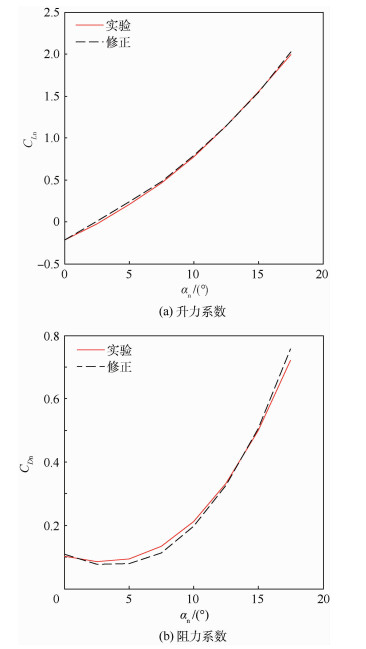 |
| 图 7 实验和修正得到的新飞行器升力系统与阻力系数随攻角变化的曲线 Fig. 7 Curves of lift coefficient and drag coefficient of new vehicle from experiment and offset correction changing with attack angle |
| 图选项 |
同理使用式(15)、式(16)可以得到c=2.9908、dD=-0.1400, 迁移可以得到Ma=13,h=40 km处的阻力力系数如图 7(b)所示。由于增加了修正参数使得迁移误差在α < 18°时最大误差控制5%以内。由于这里迁移用到的新飞行器的气动参数仅为表 1中的4个特征点,如果需要进一步提高迁移精度, 可以增加新飞行器特征点的个数来实现。
为了对新飞行器高度方向建模, 需要使用前面给出的建模方法获得新飞行器其他高度的气动参数。采用本文给出的建模方法对新飞行器70 km处建模, 可以得到整个70 km空域中新飞行器高超声速下的气动参数。Ma=13、α=7.5°时不同高度下的轴向力系数CX和法向力系数CY如图 8所示; Ma=11、α=12°时不同高度下的轴向力系数和法向力系数如图 9所示。由于这里拟合用到的气动参数是通过迁移得到的, 容易造成误差的累加, 使得高度上的建模误差达到了10%。需要提高建模精度时, 可以通过式(13)和式(15)迁移得到更多高度上的气动参数来拟合式(9)中的2个未知量。
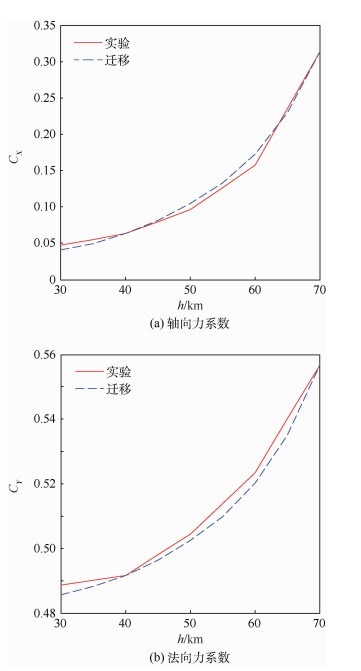 |
| 图 8 Ma=13、α=7.5°时新飞行器气动参数随高度变化的曲线 Fig. 8 Curves of aerodynamic parameters of new vehicle changing with altitude when Ma=13, α=7.5° |
| 图选项 |
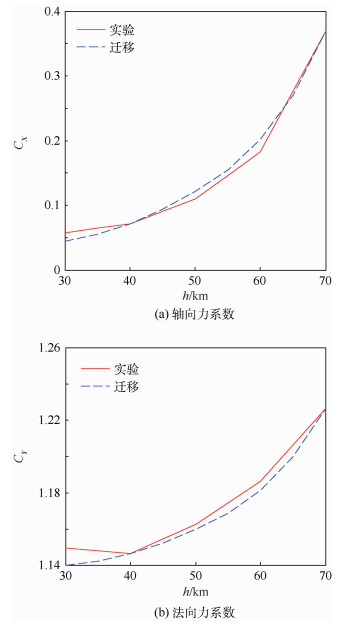 |
| 图 9 Ma=11、α=12°时新飞行器气动参数随高度变化的曲线 Fig. 9 Curves of aerodynamic parameters of new vehicle changing with altitude when Ma=11, α=12° |
| 图选项 |
4 结论 1)?利用仿射相似理论提供了评估飞行器气动外形相似度的方法, 有利于评估计算三维飞行器模型仿射相似度的值。
2)?研究了模型迁移理论在高超声速飞行器建模中的应用方法, 通过充分利用不同飞行器间的相似性,能有效减少新飞行器建模过程中的实验量,从而达到减小实验成本缩短建模周期的目的。仿真表明, 使用模型迁移方法对新飞行器进行建模, 能取得满意的建模效果。
参考文献
| [1] | LU J, GAO F. Process modeling based on process similarity[J].Industrial & Engineering Chemistry Research, 2008, 47(6): 1967–1974. |
| [2] | LU J, YAO Y, GAO F. Model migration for development of a new process model[J].Industrial & Engineering Chemistry Research, 2008, 48(21): 9603–9610. |
| [3] | LU J, GAO F. Model migration with inclusive similarity for development of a new process model[J].Industrial & Engineering Chemistry Research, 2008, 47(23): 9508–9516. |
| [4] | COX R N, CRABTREE L F. Elements of hypersonic aerodynamics[M]..London: The English Universities Press LTD., 1965: 18-55. |
| [5] | HAYES W. Hypersonic flow theory[M].New York: Academic Press, 2012: 36-67. |
| [6] | 瞿章华, 刘伟, 曾明, 等. 高超声速空气动力学[M].长沙: 国防科技大学出版社, 2001: 40-47.QU Z H, LIU W, ZENG M, et al. Hypersonic aerodynamics[M].Changsha: National University of Defense Technology Publishing, 2001: 40-47.(in Chinese) |
| [7] | NEICE S E, EHRET D M. Similarity laws for slender bodies of revolution in hypersonic flow[J].Journal of the Aeronautical Science, 1951, 18(8): 527–538.DOI:10.2514/8.2029 |
| [8] | VANDYKE M D. The combined supersonic-hypersonic similarity rule[J].Journal of the Aeronautical Sciences, 2012, 18(7): 499–500. |
| [9] | HAMAKER F M, NEICE S E, EGGERS JR A J.The similarity law for hypersonic flow about slender three-dimensional shapes:NO.NACA-TN-2443[R].Washington, D.C.:National Aeronautics and Space Administration Moffett Field Caames Research Center, 1951:1-22. |
| [10] | 张涵信. 高超声速空气动力学[M].长沙: 国防科技大学出版社, 1982: 32-50.ZHANG H X. Hypersonic aerodynamics[M].Changsha: National University of Defense Technology Publishing, 1982: 32-50.(in Chinese) |
| [11] | ANDERSON J D. Hypersonic and high temperature gas dynamics[M].New York: Mc Graw-Hill Book Company, 1989: 2-12. |
| [12] | SCHLICHTING H, GERSTEN K. Boundary-layer theory[M].London: Springer, 2000: 23-57. |
| [13] | MORGAN B, DURAIAMY K, NGUYEN N, et al. Flow physics and RANS modeling of oblique shock/turbulent boundary layer interaction[J].Journal of Fluid Mechanics, 2013, 729: 231–284.DOI:10.1017/jfm.2013.301 |
| [14] | JAUNET V, DEBIEVE J F, DUPONT P. Length scales and time scales of a heated shock-wave/boundary-layer interaction[J].AIAA Journal, 2014, 52(11): 2524–2532.DOI:10.2514/1.J052869 |
| [15] | FEDOROV A V, MALMUTH N D. Application of similarity in hypersonic transition prediction[J].AIAA Journal, 1995, 33(8): 1523–1525.DOI:10.2514/3.12578 |
| [16] | HERMES V, OLIVIER H. On the transformation of the angle of attack for supersonic similarity rules[J].Journal of Aircraft, 2013, 50(1): 302–304.DOI:10.2514/1.C031708 |
| [17] | 叶友达. 高空高速飞行器气动特性研究[J].力学进展, 2009, 39(4): 387–397.YE Y D. Study on aerodynamic characteristics of high velocity vehicle flying at high altitede[J].Advances in Mechanics, 2009, 39(4): 387–397.(in Chinese) |
