目前,针对太赫兹SAR成像已有一些研究和应用。文献[6]介绍了基于逆合成孔径雷达(ISAR)技术且采用线性调频连续波(FMCW)的太赫兹雷达成像系统,通过二维傅里叶变换法和反向投影(BP)算法实现二维高分辨率成像。文献[7]则在太赫兹时域雷达基础上,采用改进的BP算法对多种模型进行了系统的成像研究,验证了散射太赫兹时域信号的成像机制。文献[8]研究了140 GHz的ISAR实时成像系统,采用距离-多普勒(RD)算法等实现快速成像。
然而,随着载波频率的升高,成像结果对平台运动误差越敏感,运动补偿难度也越大。对于气流干扰、飞行操作等因素造成的载机偏离航线等低频运动误差,SAR系统通常可基于运动传感器数据进行补偿,但对于机载平台高频振动,尽管其幅度微小不足以影响飞行航迹,却会对太赫兹频段回波的相位发生调制而恶化成像质量[9-12]。高精度振动补偿是实现ViSAR功能的关键。直升机是未来ViSAR应用的主要平台之一,其飞行速度较快时振动幅度可达到数毫米[13-14]。由于现有的运动传感器系统一般无法精确测量毫米量级的位置偏移,因此实现ViSAR振动补偿需要基于回波数据对振动相位误差进行估计。
相较于正侧视,工作在斜视模式的ViSAR波束指向更灵活,能对平台侧前方和侧后方进行多次成像,重访敏感区域;且能保证载机的隐蔽性和安全性等。因此斜视ViSAR在敌情侦查、战场打击等军事应用中具有明显优势[15]。文献[16]讨论了一种基于回波数据的直升机载SAR振动补偿成像方法,本文基于此,针对斜视模式,提出了一种改进的平台高频振动补偿成像算法。该算法首先根据运动补偿原理在时域校正回波信号的大距离走动,并补偿距离模型三次项相位以提高方位向聚焦精度,接下来在二维频域进行多普勒Keystone变换以校正斜视时成对回波引起的距离走动,最终构造补偿函数从而在多普勒域对平台振动引起的正弦调制相位误差实现统一补偿。通过在点目标、场景回波仿真中加入直升机随机振动误差,进行仿真验证,补偿结果表明了该算法的有效性。
1 斜视ViSAR信号模型 图 1给出了直升机载平台振动情况下对地面某静止点目标T(x0, y0)的斜视振动成像几何模型。图中:斜视角θ为雷达天线波束中心方向与飞行方向的夹角;C为场景中心;rC为场景中心斜距。直升机在高度H处沿OX轴方向飞行,速度为v,在方位向t=0时刻由点P1出发经过t0后达到点P2,此时飞机与点目标T之间的距离为r(t)。机身振动导致雷达设备振动,假设设备振动方向与OZ轴的夹角为?0,振动方向和OZ轴构成的平面与OY的夹角为θ0,则可得图右上雷达天线相位中心坐标系x′y′z′e,其中点e表示不存在振动情况下相位中心的位置,点e′表示受到振动影响下的瞬时相位中心,相位中心在y′ez′坐标平面内的线段ee′上以点e为中心做简谐振动。简谐振动公式如下:
 | (1) |
 | (2) |
 |
| 图 1 斜视ViSAR平台振动几何 Fig. 1 Squint ViSAR platform vibration geometry |
| 图选项 |
式中:Am为振动幅度;fm为振动频率;φm为振动初相。当|fm·Ta|≥1时,平台的振动为高频振动,Ta为合成孔径时间。根据图 1,推导可得平台振动影响下的斜距:
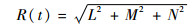 | (3) |
式中:
 |
最终可得
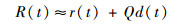 | (4) |
式中:Q=cosαcos?0-cos (β+θ0) sinαsin?0,α为天线相位中心下视角,由于太赫兹频段合成孔径时间极短,α近似保持不变,β=arctan[(x0-vt)/y0],变化范围通常小于1°,因而Q可看作常数。令A=AmQ,表示等效振动幅值,则式(4)写作
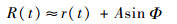 | (5) |
对于斜距r(t),定义斜视ViSAR数据采集平面成像几何如图 2所示,以照射区域中心点C为原点重新定义场景坐标系,距离方向y与rC相同,方位方向x与之垂直,设r0为波束中心扫过点目标时的斜距,则任意时刻点目标T(x0, y0)与天线相位中心之间的距离r(t)可表示为
 | (6) |
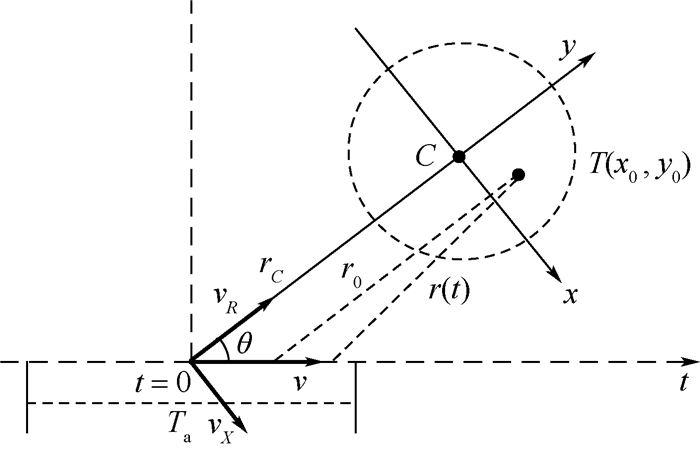 |
| 图 2 斜视ViSAR数据采集平面成像几何 Fig. 2 Squint ViSAR data acquisition plane imaging geometry |
| 图选项 |
将r(t)在t=0处做Taylor展开,则有
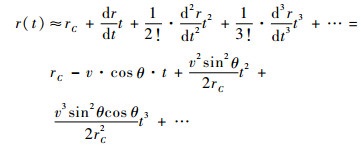 | (7) |
若发射信号采用线性调频连续波,则接收端回波信号表达式为
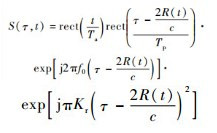 | (8) |
式中:f0为载波频率;τ为距离向时刻;Kr为距离向脉冲调频率;rect (·)为矩形窗函数;Tp为脉冲时宽;c为光速。
2 大斜视太赫兹ViSAR平台振动补偿 对于图 2所示斜视成像几何,将平台速度矢量在孔径中心时刻做如图所示的分解,即分解为正侧视速度分量vX=vsinθ和与之垂直的径向速度分量vR=vcosθ。等效平台工作在速度为vX的正侧视模式,而vR分量引起的平台运动视作是垂直航迹向的运动误差,则可将斜视成像当作加入运动补偿的正侧视成像来处理[17-19]。
平台偏离假想正侧视航迹的大小为Δr(t)=vRt,按运动补偿的处理方式,对每个方位时刻t应当补偿相位4πΔr(t)/λ。对于等效正侧视航迹模型,雷达与目标间的距离为
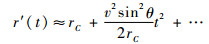 | (9) |
与式(7)相比,式(9)少了一次项,即偏离等效正侧视航迹的距离走动项,首先应对该相位进行补偿。将去调频及RVP消除后的回波信号乘以时域走动校正因子
 | (10) |
式中:fr为距离向频率。与式(7)相比,式(9)还少了三次项,该项在合成孔径时间内所产生的距离弯曲量为
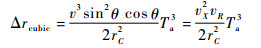 | (11) |
对于太赫兹系统,以表 1参数为例,斜视角为30°时可得|Δrcubic|=1.73mm,小于距离分辨率0.09m,但又远超过了λ/16=0.09mm,也就是说不会影响距离徙动的校正,但会影响方位向的聚焦,因此对该相位进行补偿,三次相位补偿因子表达式为
 | (12) |
表 1 仿真参数 Table 1 Simulation parameters
| 参数 | 数值 |
| 载波频率f0/GHz | 200 |
| 场景中心斜距rC/km | 2 |
| 直升机飞行速度v/(m·s-1) | 50 |
| 脉冲重复频率PRF/kHz | 3 |
| 脉冲带宽Tp/GHz | 1.5 |
| 距离向采样频率Fs/GHz | 1.8 |
表选项
至此,对回波信号已完成“运动补偿”的预处理。接下来采用改进的基于多普勒Keystone变换的方法继续对回波信号进行处理。对信号进行方位向傅里叶变换,可得其二维频域表达式为
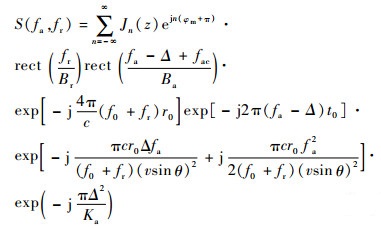 | (13) |
式中:fa为方位向频率;fac为多普勒中心频率或方位向中心频率;Br和Ba分别为距离向和方位向信号带宽;Jn(z)为n阶贝塞尔级数;z=4π(f0+fr)A/c,Δ=nfm;斜视模式下方位向调频率Ka=-2v2sin2θ/λr0。式(13)中,第3个相位表达式的第1项为斜视模式下平台振动引起的距离走动相位,第2项为斜视模式下距离频率和方位频率二次项的耦合相位,最后一个相位是成对回波引起的残余视频相位。
为消除平台振动引起的距离徙动,对式(13)进行第1次Keystone变换,即令
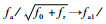
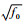
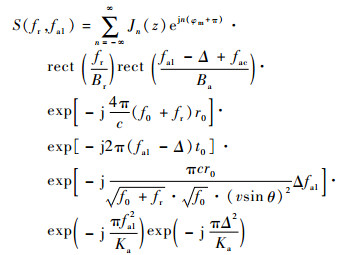 | (14) |
对信号在距离向做逆傅里叶变换(IFFT),即变换到距离多普勒域,使用如下因子表达式对其进行补偿,从而消除式(14)中的方位向二次项相位。
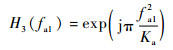 | (15) |
接下来将信号再次变换到二维频域,进行第2次Keystone变换,令
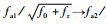
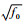
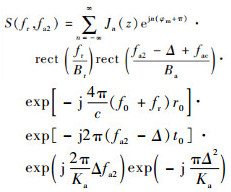 | (16) |
对比式(13)可知,此时由平台振动引起的距离徙动得到校正。但回波信号仍存在由成对回波引起的残余视频相位。为消除此残余视频相位,将信号变换到二维时域,乘以如下的相位补偿因子:
 | (17) |
最后,将信号变换到距离多普勒域,其表达式如下:
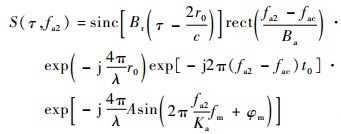 | (18) |
至此,成对回波的频域历程一致,式(18)中包含的最后一项即为平台振动相位误差的解析式。通过采用文献[20]中的参数化自聚焦方法估计,可以得到直升机振动参数,即振动幅度、频率和初相等,再按照式(18)构造补偿函数,实现振动相位误差补偿,补偿因子表达式为
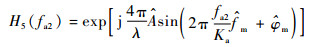 | (19) |
完整的算法流程如图 3所示。
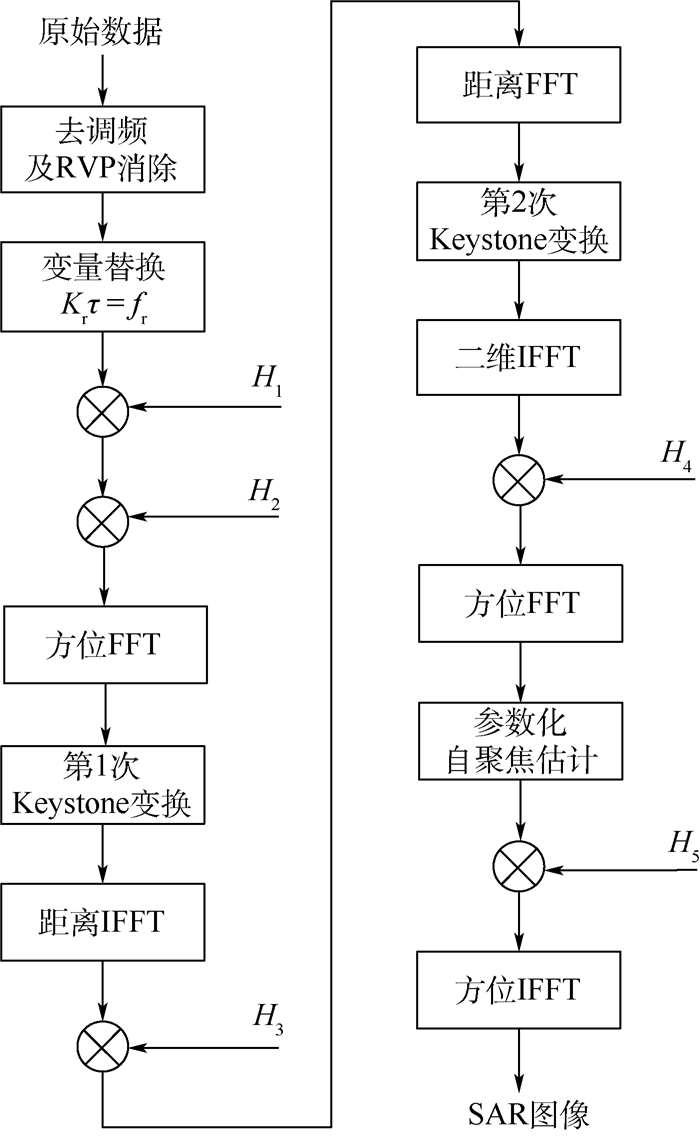 |
| 图 3 斜视太赫兹ViSAR振动补偿成像算法流程 Fig. 3 Flow of squint terahertz ViSAR vibration compensation imaging algorithm |
| 图选项 |
3 仿真实验 根据直升机载平台振动特点,设置平台振动频率为20Hz,振动幅度为1mm,在仿真中加入直升机平台振动误差,其他系统参数如表 1所示,进行如下实验。
设置斜视角θ=60°,在图 2所示场景坐标系中布置3个点目标,其位置分别为:[0,0]m,[-3,6]m,[3,6]m。分别采用传统的波数域Omega-K算法和本文的斜视太赫兹ViSAR振动补偿算法进行成像,结果如图 4所示。显然,传统斜视成像算法不能抑制成对回波,点目标散焦严重(见图 4(a)),而本文算法能有效地消除成对回波,实现点目标的聚焦成像(见图 4(b))。对振动补偿后的坐标为[3,6]m的点目标进行成像质量分析,结果见图 5。其方位向和距离向的输出分辨率分别为0.072m和0.091m,峰值旁瓣比分别为-13.10dB和-13.23dB,积分旁瓣比分别为-9.72dB和-9.81dB。已知方位向和距离向的名义分辨率为0.07m和0.09m,可见,斜视模式下点目标聚焦良好。
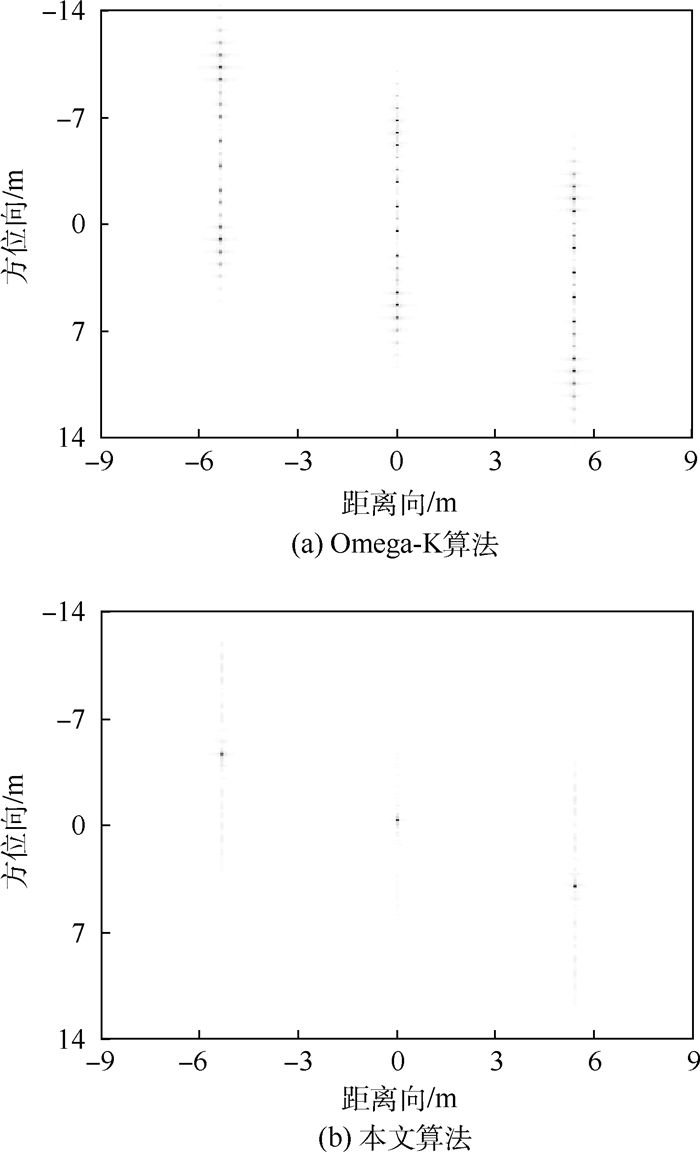 |
| 图 4 点目标成像仿真结果对比 Fig. 4 Comparison of point target imaging simulation results |
| 图选项 |
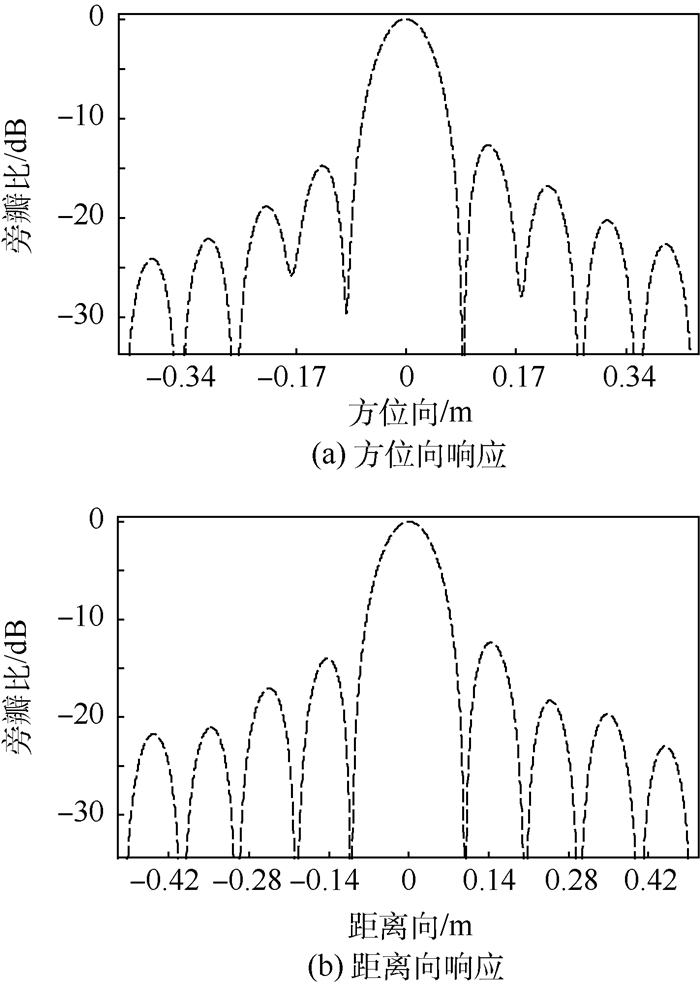 |
| 图 5 点目标成像质量分析 Fig. 5 Point target imaging quality analysis |
| 图选项 |
此外,利用多点目标仿真坦克模型,斜视角θ=30°时的结果见图 6。其中,图 6(b)为成对回波聚焦结果,即振动引起的“鬼影”;图 6(c)为振动相位误差补偿后结果,此时“鬼影”已被消除,坦克的轮廓清晰可见,大斜视时成像效果良好。
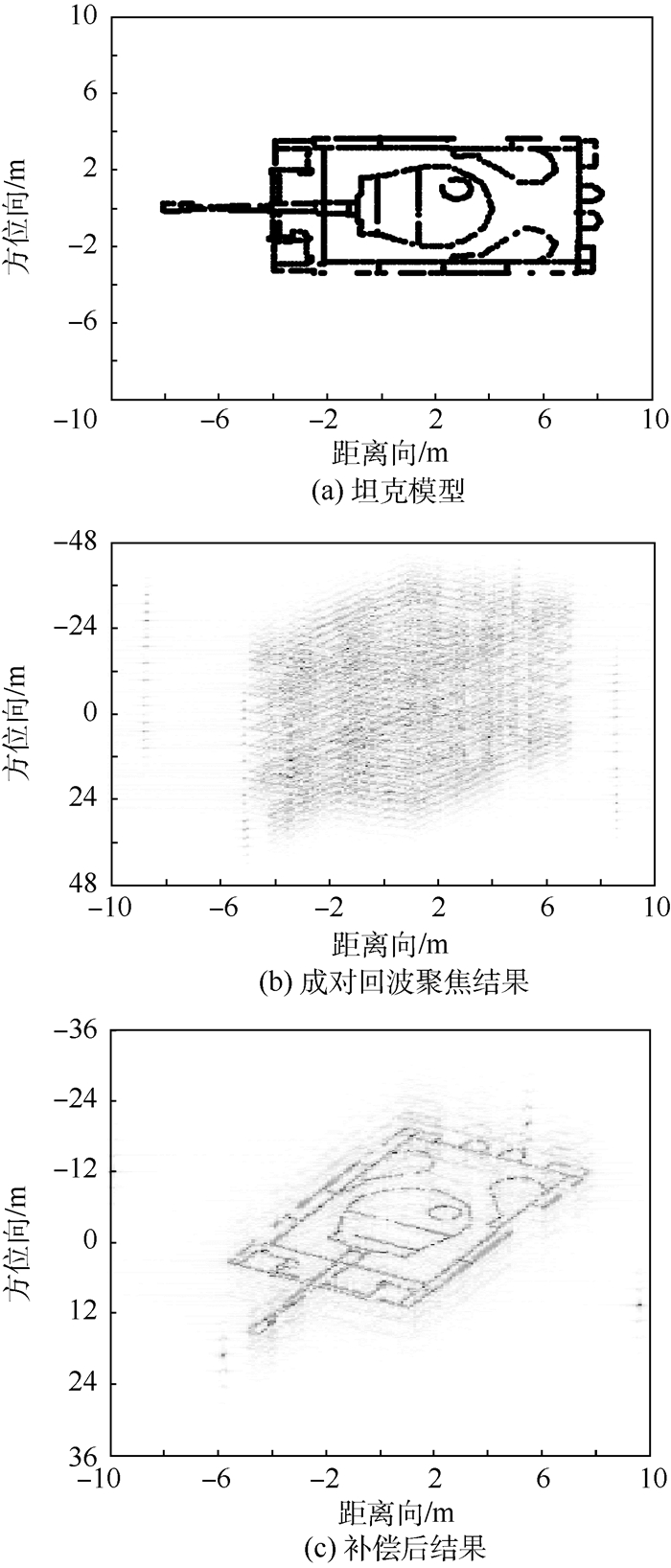 |
| 图 6 多点目标成像仿真结果 Fig. 6 Multi-point target imaging simulation results |
| 图选项 |
最后给出分布场景仿真实验,首先利用斜视逆成像算法产生回波数据,然后采用本文提出的算法进行处理,斜视角θ=30°时的仿真结果如图 7所示。图 7(b)为成对回波聚焦结果,图 7(c)为振动补偿后结果。
 |
| 图 7 分布场景成像仿真结果 Fig. 7 Distributed scene imaging simulation results |
| 图选项 |
4 结论 对于工作在太赫兹频段的ViSAR系统,直升机平台高频振动会造成ViSAR散焦,针对这一问题,本文提出了一种斜视模式下的太赫兹ViSAR振动相位误差补偿算法。仿真实验表明:
1)在正侧视等效模型的基础上,采用三次相位误差补偿,可以有效实现大斜视ViSAR的聚焦成像处理,且具有成像处理流程简洁、与正侧视模式成像算法兼容度高的优点。
2)针对直升机平台高频振动引起的成对回波散焦问题,采用多普勒Keystone变换能够实现成对回波虚像的聚焦,进而可用自聚焦方法实现成对回波的抑制处理。
3)大斜视(例如斜视角为30°)时,该算法亦能实现对点目标或分布场景回波信号的振动相位误差补偿,且成像质量良好。
参考文献
| [1] | MILLER J, BISHOP E, DOERRY A.An application of backprojection for Video SAR image formation exploiting a subaperture circular shift register[C]//Proceedings of Society of Photo-Optical Instrumentation Engineers.Bellingham, WA:SPIE, 2013, 4:1-14. |
| [2] | DAMINI A, MANTLE V, DAVIDSON G.A new approach to coherent change detection in VideoSAR imagery using stack averaged coherence[C]//2013 IEEE Radar Conference.Piscataway, NJ:IEEE Press, 2013, 4:1-5. |
| [3] | CHENG B B, JIANG G, WANG C. Real-time imaging with a 140 GHz inverse synthetic aperture radar[J].IEEE Transactions on Terahertz Science and Technology, 2013, 3(5): 594–605.DOI:10.1109/TTHZ.2013.2268317 |
| [4] | 梁美彦, 邓朝, 张存林. 太赫兹雷达成像技术[J].太赫兹科学与电子信息学报, 2013, 11(2): 189–196.LIANG M Y, DENG Z, ZHANG C L. Terahertz radar imaging technology[J].Journal of Terahertz Science and Electronic Information, 2013, 11(2): 189–196.(in Chinese) |
| [5] | HEREMANS R, VANDEWAL M, ACHEROY M.Synthetic aperture imaging extended towards novel THz sensors[C]//2008 IEEE Sensors, SENSORS 2008.Piscataway, NJ:IEEE Press, 2008:438-441. |
| [6] | ZHANG B, PI Y M, LI J. Terahertz imaging radar with inverse aperture synthesis techniques:System structure, signal processing, and experiment results[J].IEEE Sensors Journal, 2015, 15(1): 290–299.DOI:10.1109/JSEN.2014.2342495 |
| [7] | 魏明贵, 梁达川, 谷建强, 等. 太赫兹时域雷达成像研究[J].雷达学报, 2015, 4(2): 222–229.WEI M G, LIANG D C, GU J Q. Terahertz radar imaging based on time-domain spectroscopy[J].Journal of Radars, 2015, 4(2): 222–229.(in Chinese) |
| [8] | CHENG B B, JIANG G, WANG C. Real-time imaging with a 140 GHz inverse synthetic aperture radar[J].IEEE Transactions on Terahertz Science and Technology, 2013, 3(5): 594–604.DOI:10.1109/TTHZ.2013.2268317 |
| [9] | 林华. 无人机载太赫兹合成孔径雷达成像分析与仿真[J].信息与电子工程, 2010, 8(4): 373–377.LIN H. Analysis and simulation of UAV terahertz wave synthetic aperture radar imaging[J].Information and Electronic Engineering, 2010, 8(4): 373–377.(in Chinese) |
| [10] | 沈斌.THz频段SAR成像及微多普勒目标检测与分离技术研究[D].成都:电子科技大学, 2008:27-28.SHEN B.THz-SAR imaging and micro-Doppler target detection and separation[D].Chengdu:University of Electronic Science and Technology of China, 2008:27-28(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10614-2008122099.htm |
| [11] | KIRK J. Motion compensation for synthetic aperture radar[J].IEEE Transactions on Aerospace and Electronic Systems, 1975, 11(3): 338–348. |
| [12] | 赵雨露, 张群英, 李超. 视频合成孔径雷达振动误差分析及补偿方案研究[J].雷达学报, 2015, 4(2): 230–239.ZHAO Y L, ZHANG Q Y, LI C. Vibration error analysis and motion compensation of video synthetic aperture radar[J].Journal of Radars, 2015, 4(2): 230–239.(in Chinese) |
| [13] | HONG X R, ZHANG T, DU Z C.Helicopter-borne SAR imaging processing of chirp-stepped signal[C]//2006 CIE International Conference on Radar.Piscataway, NJ:IEEE Press, 2006:1-5. |
| [14] | CERUTI A, LIVERANI A, RECANATESI L.Improving helicopter flight simulation with rotor vibrations[C]//Proceedings of International Conference on Innovative Methods in Product Design, 2011:636-645. |
| [15] | 梁毅, 王虹现, 邢孟道. 基于FMCW的大斜视SAR成像研究[J].电子与信息学报, 2009, 31(4): 776–780.LIANG Y, WANG H X, XING M D. Imaging study of high squint SAR based on FMCW[J].Journal of Electronics and Information, 2009, 31(4): 776–780.(in Chinese) |
| [16] | WANG H, ZHANG Y, WANG B B.A novel helicopter-borne terahertz SAR imaging algorithm based on Keystone transform[C]//International Conference on Signal Processing.Piscataway, NJ:IEEE Press, 2014:1958-1962. |
| [17] | 周峰, 王琦, 邢孟道. 一种机载大斜视SAR运动补偿方法[J].电子学报, 2007, 35(3): 463–468.ZHOU F, WANG Q, XING M D. A squint airborne SAR motion compensation method[J].Chinese Journal of Electronics, 2007, 35(3): 463–468.(in Chinese) |
| [18] | 吴勇, 宋红军, 彭靳. 基于时域去走动的SAR大斜视CS成像算法[J].电子与信息学报, 2010, 32(3): 593–598.WU Y, SONG H J, PENG J. Chirp scaling imaging algorithm of SAR in high squint mode based on range walk removal[J].Journal of Electronics and Information, 2010, 32(3): 593–598.DOI:10.3724/SP.J.1146.2009.00472(in Chinese) |
| [19] | MOREIRA A, HUANG Y. Airborne SAR processing of highly squinted data using a chirp scaling approach with integrated motion compensation[J].IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(5): 1029–1040.DOI:10.1109/36.312891 |
| [20] | ZHANG Y, SUN J P, LEI P, et al. SAR-based paired echo focusing and suppression of vibrating targets[J].IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(12): 7593–7605.DOI:10.1109/TGRS.2014.2314681 |
