多输入多输出(Multiple-Input Multiple-Output,MIMO)系统可以在不增加系统带宽和传输功率的前提下，利用空间自由度(Degrees of Freedom，DOF)来成倍地提高无线信道的容量。然而，即使将MIMO技术应用到多网络系统中，由于网络之间消息相互干扰，系统性能受到干扰的影响还是很严重。因为研究无线网络容量一般较为困难，可以用空间自由度进行近似。关于MIMO无线网络现有研究中，已经有对点对点(Point to Point,PTP)信道、广播信道(Broadcast Channel，BC)、多址接入信道(Multiple Access Channel,MAC)、干扰信道(Interference Channel,IC)和X信道(X Channel，XC)等单个信道的自由度研究。多用户信道并存网络模型的自由度研究却很少。在无线网络中，干扰是限制信道自由度的一个主要因素。尤其是多个网络并存时，网络内部和网络之间都会有干扰，那么对干扰进行处理在研究信道的自由度中就显得尤为重要。干扰处理的方法主要有干扰回避、干扰正交化、干扰对齐和干扰中和等，本文主要用到干扰对齐。干扰对齐^[1]的基本思想是：通过收发端的联合设计，使得在每个接收端其收到的干扰可以尽量地对齐到信号空间的某些维度，达到压缩干扰占用空间、增大期望信号可用空间的目的；同时还要保持期望信号与干扰信号相互独立，期望信号处于零干扰的空间中，这样期望信号才能够被解析出来。由于干扰对齐的重要性，干扰对齐技术在很多模型中被得到广泛应用。干扰对齐的具体实现方法有很多，比如线性干扰对齐、渐近干扰对齐和盲干扰对齐等。其中，线性干扰对齐的方案是最容易实现也是最常用的一种方法，主要基于线性预编码(波束成形)机制的信号空间对齐方法。波束成型方案在现存的MIMOPTP信道、BC和MAC中应用非常普遍，例如K用户的IC中，通过线性干扰对齐，每个用户可以得到1/2的自由度^[1]；在M×N用户的XC^[2]中，通过线性干扰对齐方案^[3]能达到MN/(M+N-1) 的自由度。
过去的研究中已经通过干扰对齐和干扰中和方法获知了PTP信道、BC、MAC、IC和XC等简单信道的自由度^[4-9]。对于更加复杂的信道，如2个或多个简单信道共存构成的复合信道，这些复合信道的自由度研究仅有少量的进展。文献^[6]推导了2个PTP信道并存时的网络模型的自由度。在2个BC并存时的自由度研究^[7-8]中，比较发现，使用干扰对齐的方法比使用迫零方法得到的自由度要大。同样，使用干扰对齐方法也研究得出了2个MAC共存的网络模型的自由度^[9]。所以，干扰对齐在复杂网络中的应用越来越广泛。
本文中研究的是2×2 XC与PTP 信道2种信道共存时网络整体的自由度，这是一种新的并存模型。不同于认知无线电^[10]中主次网络次序不同的假设，本文模型中2个信道的次序可以无关；尽管如此，依然借用了主网与次网的概念来描述与区分所涉及的2个信道。使用渐近干扰对齐方法，证明其可达自由度为5/3；另一方面，目前找到的自由度上界为2。
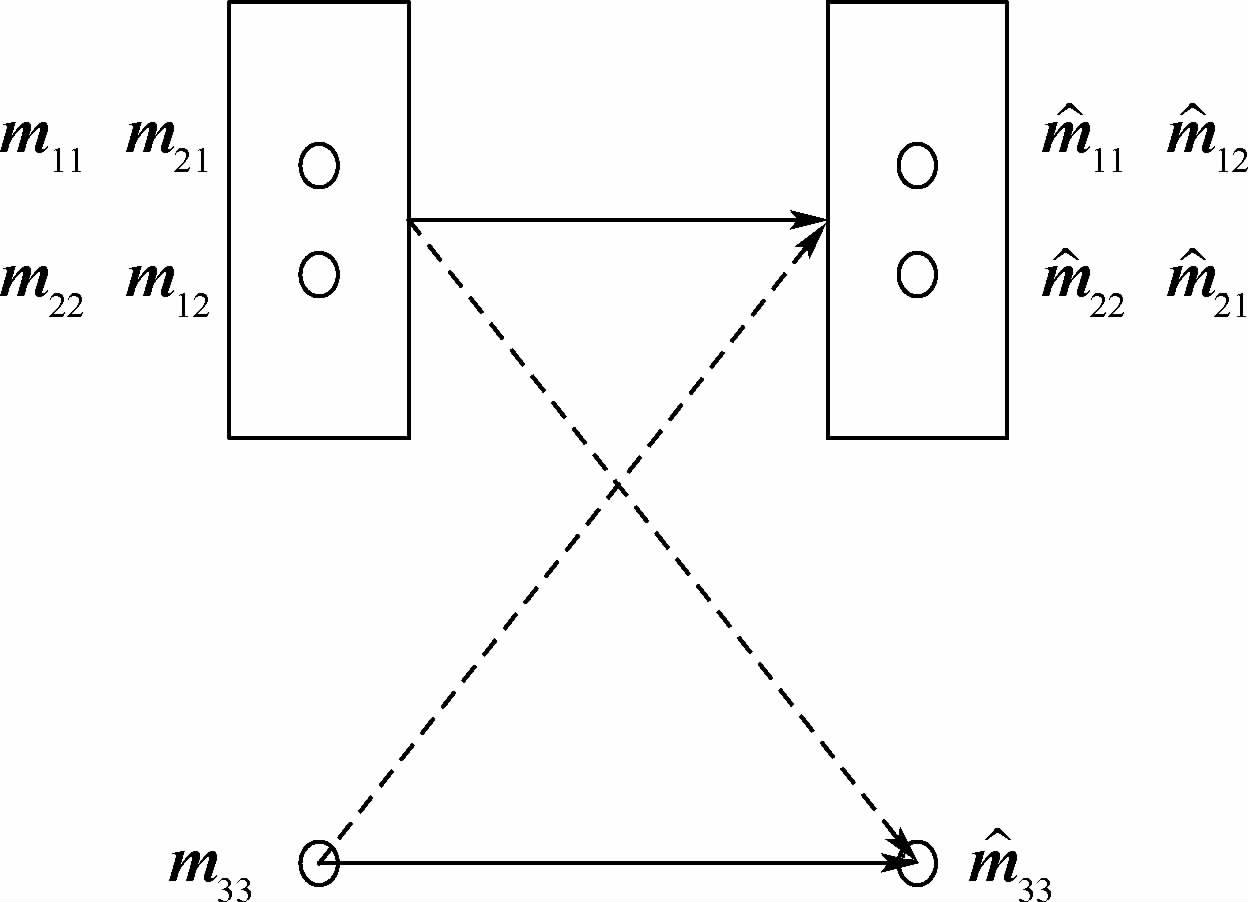
符号说明：本文中的m_ij为发送端j发送到接收端i相应的消息；$\hat{m}$_ij为接收端i的期望信号； diag(a₁,a₂,…,a_N)为对角元素为a₁,a₂,…,a_N的对角阵；(·)^T为向量或矩阵的转置；C_ij为矩阵第i行第j列元素的代数余子式。
1 系统模型 本文研究的2×2 XC与PTP信道并存系统模型如图 1所示，上方虚线框图内的2×2 XC代表主网络，下方虚线框图内的PTP信道代表次网络(图 2和图 3中的图形均适用)。

图 1 2×2 XC和PTP信道共存模型 Fig. 1 Coexistence model of 2×2 XC and PTP channel

图选项

图 2 基于传播时延对自由度的分析图 Fig. 2 Analysis diagram of DOF based on propagation delay

图选项

图 3 自由度上界分析图 Fig. 3 Analysis of upper bound on DOF

图选项

主网络是2×2 XC，次网络是PTP信道，考虑每个节点仅有一根天线的基本情况。由于单天线导致信号空间不足以进行信号处理，采用符号扩展^[11-14]的方法来进行分析，这样收发端才有足够的空间可以信号检测与干扰处理。注意：得到的自由度结论需要除以所用的符号扩展数目，即进行归一化处理^[15-16]才能与原模型相对应。
消息与干扰情况说明如下：m₁₁、m₂₁为发送端1要发送的2个消息，m₂₂、m₁₂为发送端2要发送的2个消息，m₃₃为发送端3要发送的消息，则发送端总共发送5个消息。为了不失一般性，假设各发送端信号满足功率约束关系：E{X_i²}≤P，其中：X_i为发送信号；E为数学期望，P为功率。图 1中实线代表的是发送端向对应接收端发送的期望信号，虚线代表的是对此接收端的干扰信号。接收端1的期望消息是m₁₁、m₁₂，其他3个消息是干扰消息；接收端2的期望消息是m₂₁、m₂₂，其他3个消息是干扰消息；接收端3的期望消息是m₃₃，其余4个消息是干扰消息。设所用符号扩展数目为M_n。输入输出关系为

(1)

式中：Y_j为维度为M_n×1、第j(j=1,2,3)个接收端的输出信号；H_ji为发送端i到接收端j、维度为M_n×M_n的信道矩阵；v_jⁱ(j=1,2,3；i=1,2)为发送端j的第i个波束成形向量，其中v₁¹和v₂¹是(n+1)^N×1维，其他波束成形向量是n^N×1维，n为变量，自由度随n变化而变化，当n趋于无穷大时，内界可达5/3，N为2.1节中6个约束关系式分成的两部分中，每个部分的T_k个数,可得N=2；z_j(j=1,2,3)代表的是M_n×1维信道的加性高斯白噪声。
2 可达自由度 2.1 自由度下界 证明思路主要为让每个消息均获得1/3的自由度。为此，需要的符号扩展个数可以确定为M_n=2(n+1)^N+n^N，其中消息m₁₁、m₂₂各包含(n+1)^N个符号，消息m₁₂、m₂₁和m₃₃各包含n^N个符号。
定理1?2×2 XC和PTP共存的网络，使用渐近干扰对齐方法，网络自由度为5/3是可达的，其中2×2 XC自由度为4/3，PTP自由度为1/3。
证明 采用的干扰处理方案如下。
在接收端1，期望信号为m₁₁、m₁₂，干扰信号为m₂₁、m₂₂和m₃₃，输入输出关系是

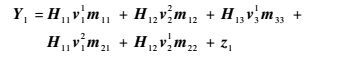因为每个消息自由度为1/3，两个期望消息已经占接收端1空间的2/3，所以只剩1/3空间。将干扰m₂₁和m₃₃对齐到m₂₂的空间中，约束条件为

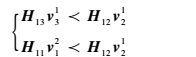(2)

式中：$\prec $表示归属于某个集合，例如a$\prec $b就是矩阵a的列向量组成的集合是矩阵b的列向量组成集合的子集。在接收端2，使用渐进干扰对齐，期望信号为m₂₁、m₂₂，干扰信号为m₁₁、m₁₂和m₃₃，输入输出关系为

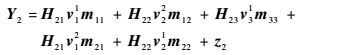将干扰m₁₂、m₃₃对齐到m₁₁的空间中，则约束条件为

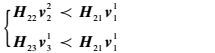(3)

在接收端3，期望信号为m₃₃，干扰信号为m₁₁、m₁₂、m₂₁和m₂₂，输入输出关系为

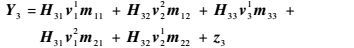因为期望信号仅占接收端空间的1/3，剩余2/3的空间放干扰消息。将干扰消息m₁₂对齐到m₁₁的空间中，干扰消息m₂₁对齐到m₂₂的空间中，则约束关系为

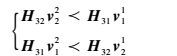(4)

由接收端1、接收端2、接收端3干扰对齐方案的约束条件式(2)、式(3)和式(4)可以得到

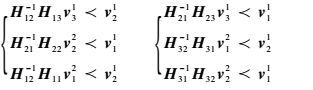(5)

令B₁=H₁₂^-1H₁₃v₃¹，对应波束成形向量v₃¹；令B₂=H₂₁^-1H₂₂v₂²，对应波束成形向量v₂²。对角阵g_i=diag(g₁₁,g₂₂,…,g_n^Nn^N)(j=1,2,3)来自一个连续分布，以保证矩阵的随机性。令g₁v₃¹=g₂v₁²=g₃v₂²，目的是让v₃¹分别能用v₁²、v₂²表示。记：

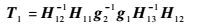(6)

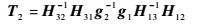(7)

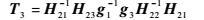(8)

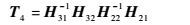(9)

通过式(6)~式(9)可以将式(5)改写为

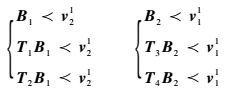(10)

令w₁和w₂为M_n×1的列向量，具体定义为

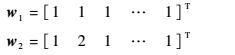这样可保证w₁和w₂线性独立。要满足条件式(10)，矩阵B₁和B₂、v₂¹和v₁¹分别从式(11)~式(14)对应的集合中选取。

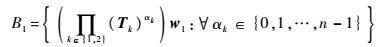(11)

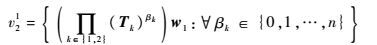(12)

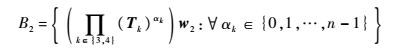(13)

(14)

要使接收端的期望信号能被解析出来，需要期望信号与干扰信号是相互独立的，即期望信号与干扰信号构成的空间是满秩的。即证明矩阵接收端1的信号空间[H₁₁v₁¹H₁₂v₂²H₁₂v₂¹]是满秩的。矩阵[H₁₁v₁¹H₁₂v₂²H₁₂v₂¹]左乘H₁₁ ^-1得到：

w₁$\prec $S、w₂$\prec $S，显然，如果w₁和w₂不是线性独立的，则S不是满秩的。矩阵S中第l行为，要证明接收端干扰信号和期望信号是满秩的，即证明S是满秩的，这里采用反证法证明。其中α_k∈{0,1,…,n-1}，β_k∈{0,1,…,n}，d_l取自一个连续的分布函数的随机变量。用反证法证明矩阵S是满秩的，即只要推出概率P(S=0)>0(S代表S的行列式)矛盾。
证明：
1) 将矩阵S按第1行展开得到其行列式为

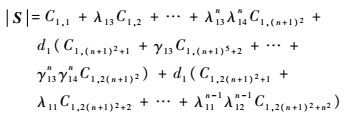(15)

如果λ_1k、γ_1k(k=1,2,3,4)的值给定，那么S=0只需满足下列条件之一：①d₁是此方程的根；②λ_1k、γ_1k的各次项系数都等于0。
由于d₁来自于一个连续的分布，所以满足上述条件①的概率几乎为零，所以下面需要证明满足条件②的概率大于0即可,即：P(S=0)>0可推出式(16)成立的概率大于0。

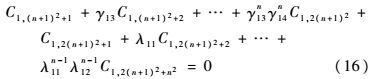(16)

2) 接下来考虑式(16)。如果λ_1k、γ_1k给定，同理要保证等式(16)成立的概率大于0，只需满足下列2个条件之一即可：①λ₁₁、λ₁₂、γ₁₃和γ₁₄是此方程的根；②λ₁₁、λ₁₂、γ₁₃和γ₁₄的各次项系数都等于0。
满足条件①的概率几乎为零，所以只需证明满足条件②的概率大于零即可。
3) 由式(16)可以推出一个充分条件，即C_{1,2(n+1)²+n²}=0的概率大于0。以此类推，按第l层展开后，得到的充分条件是C_{l,2(n+1)²+n²-l}=0成立的概率大于0。
重复之前的步骤，这样一步步将第1行最后一列的代数余子式取出来，取M_n-1次之后会推出矛盾。不失一般性，将w₁放在第1列，那么会推出“1=0”的矛盾。因此原命题得证，即期望消息和干扰消息空间独立。同理，接收端2和接收端3期望消息和干扰消息空间也是独立的。
由以上证明可得，总共发送消息符号数2(n+1)²+3n²个，符号扩展2(n+1)²+n²，自由度为$\frac{2{{\left( n+1 \right)}^{2}}+3{{n}^{2}}}{2{{\left( n+1 \right)}^{2}}+n}$。当n趋于无穷的时候，自由度达到5/3。其中，2×2 XC占用4/5，所获自由度为4/3；PTP信道占用1/5，所获自由度为1/3。
由文献^[2]可知2×2 XC本身信道自由度为4/3，点对点信道与之共存时，只要经过良好设计，可以避免2×2 XC的自由度受到影响，同时点对点信道可以获得1/3的自由度。如果以点对点信道作为主网，其自由度为1，此时如果不降低PTP信道自由度的话，由于没有多余信号空间容纳干扰，故次网XC将不能获得任何自由度。但是如果PTP信道可以降低自由度的话，XC可以获得部分自由度，此时问题回到第1节的模型。故本文研究模型适用于2个网络无优先级并存，也适用于2×2 XC作为主网优先满足其自由度的情况。
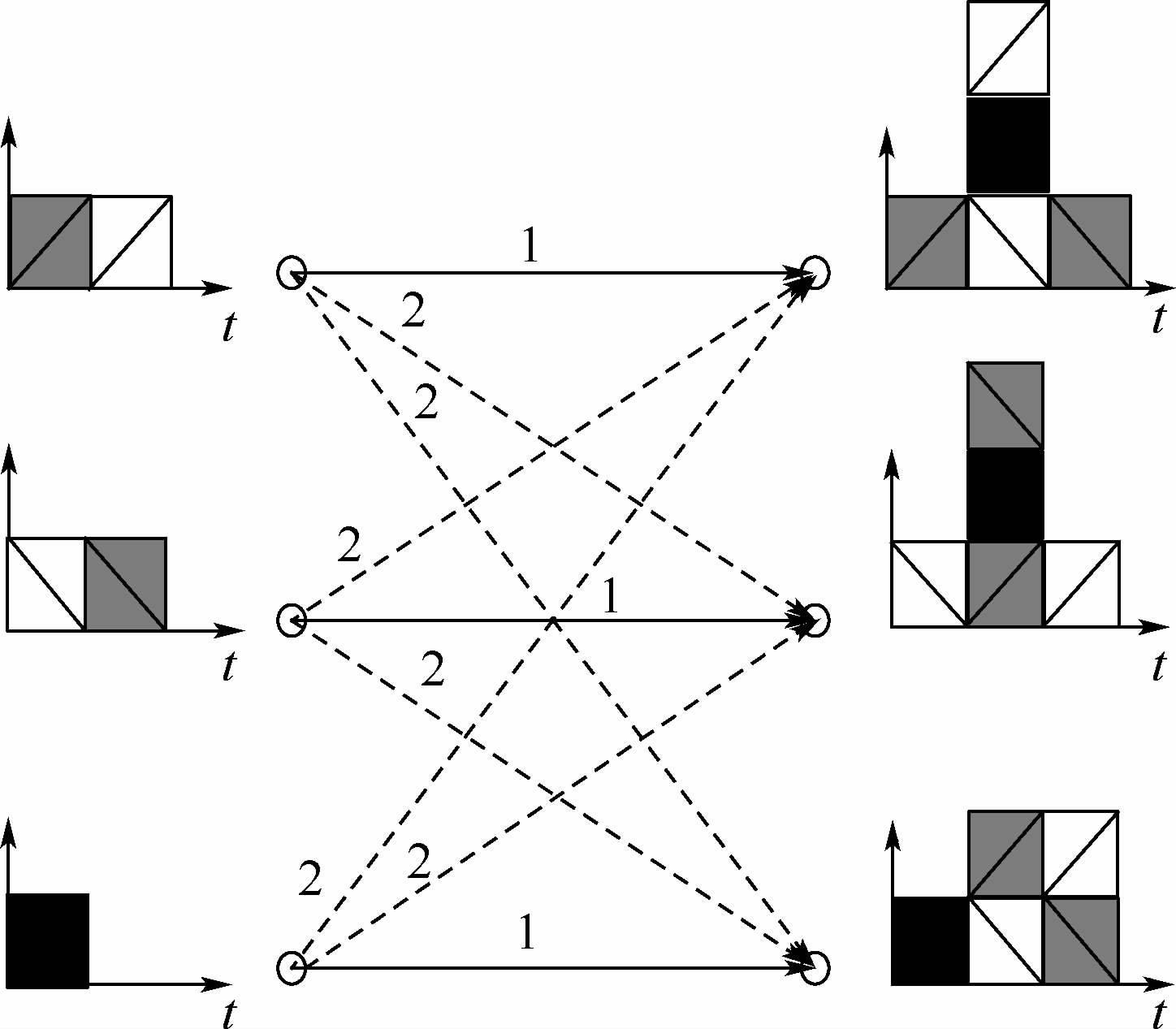
2.2 基于传播时延的例证 下面举一个特殊例子来证明2.1节自由度下界是可以达到的。基于传播时延假设，图 2中给出了5/3自由度如何达到的具体实例。图中实线代表传播时延为1，虚线代表传播时延为2，可以看出，发送端发送5个消息，灰色方块代表接收端1要接收的消息，方块中有左对角线表示发送端1发送的消息；白色方块代表接收端2要接收的消息，方块中有右对角线表示发送端2发送的消息；黑色方块代表发送端3发给接收端3的消息。
基于上述传播时延假设及消息配置，如图 2所示，发送端1在第1时隙发送灰色左对角线方块，到达接收端1存在1个传播时延；发送端2在第1时隙发送白色右对角线方块,发送端3在第1时隙发送黑色方块，它们到达接收端1有2个传播时延。在第2时隙，发送端1发送白色左对角方块消息，发送端2发送灰色右对角方块消息。接收端1在第1时隙和第3时隙得到期望消息(灰色方块)占2/3，干扰消息占1/3。同样地，在接收端2，期望消息(白色方块)占2/3，干扰消息占1/3。发送端3在第1时隙得到期望消息，第2、第3时隙得到干扰消息，从而期望消息占1/3。由系统模型传播时延的分析可得，模型自由度为2/3+2/3+1/3=5/3是可实现的。
2.3 自由度上界 根据文献^[1]，对于两用户的多输入多输出高斯干扰信道，发送端的天线数分别为M₁、M₂时，接收端的天线数分别为N₁、N₂时，其自由度为min(M₁+M₂,N₁+N₂,max(M₁,N₂),max(M₂,N₁))。
如图 3所示，将2×2 XC合并为每节点天线数为2的点对点，与次网络每节点单天线点对点组成两用户IC，即M₁=2，M₂=1，N₁=2，N₂=1，由文献^[1]得到此模型自由度为2。由于节点合并不会降低原系统自由度，故其自由度上界为2。与前面推导出的自由度下界相比，该上界较为宽松。
3 结 论 本文研究了2×2 XC与点对点信道并存时的网络模型，使用渐近干扰对齐方法分析了系统的自由度，提出了基于符号扩展的信号处理方案，证明可以达到的自由度为5/3，并给出了参考自由度上界为2。该自由度下界的证明可以为具体网络收发设计提供理论上的参考。

参考文献

[1]	CADAMBE V R, JAFAR S A. Interference alignment and degrees of freedom of the K-user interference channel[J].IEEE Transactions on Information Theory, 2008, 54(8): 3425–3441.DOI:10.1109/TIT.2008.926344
[2]	JAFAR S A, SHAMAI S. Degrees of freedom region of the MIMO X channel[J].IEEE Transactions on Information Theory, 2008, 54(1): 151–170.DOI:10.1109/TIT.2007.911262
[3]	YETIS C M,GOU T,JAFAR S A,et al.Feasibility conditions for interference alignment[C]//Global Telecommunications Conference,2009(GLOBECOM 2009).Piscataway,NJ:IEEE Press,2009:1-6.
[4]	HUANG C, JAFAR S A. Degrees of freedom of the MIMO interference channel with cooperation and cognition[J].IEEE Transactions on Information Theory, 2009, 55(9): 4211–4220.DOI:10.1109/TIT.2009.2025535
[5]	CADAMBE V R, JAFAR S A. Interference alignment and the degrees of freedom of wireless X networks[J].IEEE Transactions on Information Theory, 2009, 55(9): 3893–3908.DOI:10.1109/TIT.2009.2025541
[6]	周璐娜, 刘锋, 曾连荪. 两个点对点(PTP)网络并存时的自由度研究[J].计算机科学, 2015, 42(1): 110–112.ZHOU L N, LIU F, ZENG L S. Research on degrees of freedom of two PTP networks coexistence[J].Computer Science, 2015, 42(1): 110–112.(in Chinese)
[7]	KIM J,PARK S H,SUNG H,et al.Sum rate analysis of two-cell MIMO broadcast channels:Spatial multiplexing gain[C]//IEEE International Conference on Communications (ICC),2010.Piscataway,NJ:IEEE Press,2010:1-5.
[8]	SHIN W, LEE N, LIM J B, et al. On the design of interference alignment scheme for two-cell MIMO interfering broadcast channels[J].IEEE Transactions on Wireless Communications, 2011, 10(2): 437–442.DOI:10.1109/TWC.2011.120810.101097
[9]	LEE N,SHIN W,HEATH R W,et al.Interference alignment with limited feedback for two-cell interfering MIMO-MAC[C]//International Symposium on Wireless Communication Systems (ISWCS).Piscataway,NJ:IEEE Press,2012:566-570.
[10]	周璐娜, 刘锋, 曾连荪. CSIT对无线MIMO网络自由度的影响[J].计算机应用研究, 2014, 31(12): 3813–3817.ZHOU L N, LIU F, ZENG L S. Influence of CSIT on degrees of freedom of wireless MIMO networks[J].Application Research of Computer, 2014, 31(12): 3813–3817.(in Chinese)
[11]	TRESCH R,GUILLAUD M,RIEGLER E.On the achievability of interference alignment in the K-user constant MIMO interference channel[C]//IEEE/SP 15th Workshop on Statistical Signal Processing,2009(SSP'09).Piscataway,NJ:IEEE Press,2009:277-280.
[12]	JAFAR S A, FAKHEREDDIN M J. Degrees of freedom for the MIMO interference channel[J].IEEE Transactions on Information Theory, 2007, 53(7): 2637–2642.DOI:10.1109/TIT.2007.899557
[13]	ABDOLI M J, GHASEMI A, KHANDANI A K. On the degrees of freedom of K-user SISO interference and X channels with delayed CSIT[J].IEEE Transactions on Information Theory, 2013, 59(10): 6542–6561.DOI:10.1109/TIT.2013.2268154
[14]	LU Y, WEI Z. On degrees of freedom region of three-user MIMO interference channels[J].IEEE Transactions on Signal Processing, 2015, 63(3): 590–603.DOI:10.1109/TSP.2014.2379612
[15]	GOU T G, JAFAR S A. Degrees of freedom of the K user M×N MIMO interference channel[J].IEEE Transactions on Information Theory, 2010, 56(12): 6040–6057.DOI:10.1109/TIT.2010.2080830
[16]	LEE N, LIM J B, CHUN J. Degree of freedom of the MIMO Y channel:Signal space alignment for network coding[J].IEEE Transactions on Information Theory, 2010, 56(7): 3332–3342.DOI:10.1109/TIT.2010.2048486