合成孔径聚焦技术(SAFT)是一种超声检测三维数据重建方法,该方法对采集的所有A波数据在时间-空间域进行计算,模拟声束在试件内任意位置处聚焦,从而提高检测信号的信噪比和分辨缺陷的能力[8]。1976年,Frederick等[9]首次将SAFT用于核反应堆压力容器与管道的检测,提高了超声检测判别缺陷形状与走向的能力。根据SAFT对检测数据处理方法的不同, 可分为时域合成孔径聚焦技术(TSAFT)[8]与频域合成孔径聚焦技术(FSAFT)[10]。1992年,Busse[10]将傅里叶变换与SAFT结合,提出了FSAFT,在频率-波数域实现所有计算。与TSAFT相比,FSAFT计算效率更高,近年来得到广泛研究[10-12]。FSAFT能有效提高检测图像横向分辨率[12],因此将检测数据经FSAFT处理后再运用半波高法进行缺陷定量评价(FSAFT-DQM)这一方法理论上能够克服直接用半波高法对小于声束直径的缺陷定量时误差较大的问题,能扩展半波高法的应用范围。然而,现有研究主要集中在应用FSAFT提高检测图像分辨率,没有探讨该方法对缺陷定量的作用,更没有分析检测参数对使用该方法进行缺陷定量的影响。为此,本文对与探头焦斑尺寸相近的缺陷进行点聚焦水浸超声检测,对检测结果运用FSAFT-DQM进行缺陷定量评价,分析检测深度和扫描步距对FSAFT-DQM缺陷定量精度的影响。
1 频域合成孔径聚焦成像方法 水浸超声检测时,超声探头激发超声波经水传播至试样内,并接受试样反射回的超声波,其原始模型与等效模型如图 1所示。水浸超声平探头脉冲反射法检测试样内部缺陷时声波遇到缺陷将产生反射回波,见图 1(a)。平探头保持与工件表面垂直,平探头接收的信号可等效为从缺陷处向外辐射的超声波信号,见图 1(b)。等效模型的声程为实际声程的一半,为满足两者所接收超声信号在时间上相对应,等效模型的声速v(z)为实际声速c(z)的一半[10, 12],即v(z)=c(z)/2。
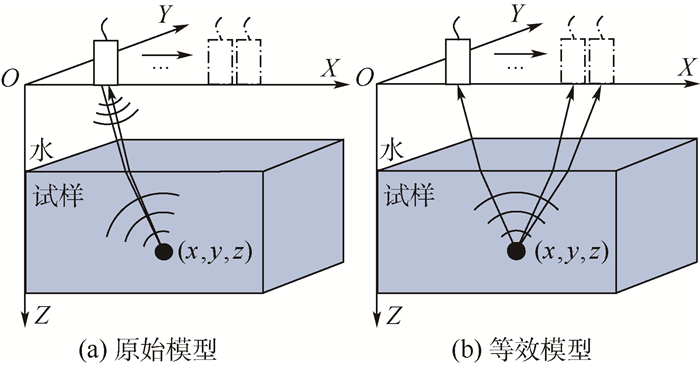 |
| 图 1 水浸超声检测原始模型与等效模型 Fig. 1 Prototype and equivalent model of immersion ultrasonic testing |
| 图选项 |
基于等效模型,以p(x, y, z, t)表示空间任意位置(x, y, z)处随时间t变化的声压。波动方程[13]为
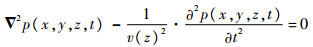 | (1) |
令P(kx, ky, z, ω)为p(x, y, z, t)的三维傅里叶变换结果,由傅里叶逆变换得
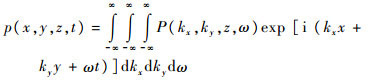 | (2) |
将式(2)代入式(1)可得
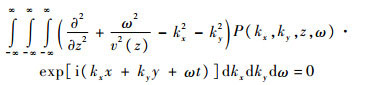 | (3) |
当ω≥0时,解式(3)得[14]
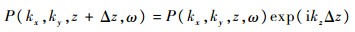 | (4) |
式中:
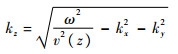 | (5) |
水浸超声检测采集到探头所在平面内声压信号,即p(x, y, 0, t),对其进行傅里叶变换可以得到P(kx, ky, 0, ω)。由式(4)可计算任意检测深度z处的P(kx, ky, z, ω)。若在检测深度z处有缺陷,则在该缺陷处存在反射声压,且在t=0时反射声场尚未发散,有利于缺陷定量评估。t=0时,由式(2)可得
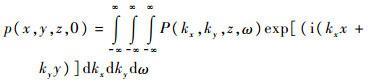 | (6) |
式(4)和式(6)的推导是基于平探头进行的,应用于聚焦探头需要进行修正。聚焦探头接收到的原始信号可转换为焦平面处假想平探头接收到的超声回波信号[12]。修正后计算公式为
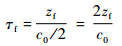 | (7) |
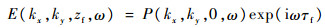 | (8) |
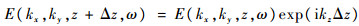 | (9) |
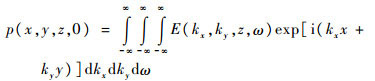 | (10) |
式中:τf为声波从探头表面传播至焦平面处所需时间;zf为探头焦距;c0为水中声速。
综上,点聚焦探头脉冲反射法检测进行FSAFT成像的具体流程如图 2所示。首先,将探头接收到的声压信号p(x, y, 0, t)进行傅里叶变换得P(kx, ky, 0, ω),依式(8)计算焦平面处角谱E(kx, ky, zf, ω);然后,依式(9)逐层计算所需检测深度范围内的角谱E(kx, ky, z, ω),逐次依式(10)计算二维成像数据p(x, y, z, 0);最后,将各检测深度二维成像数据按深度值堆叠构成FSAFT成像结果。
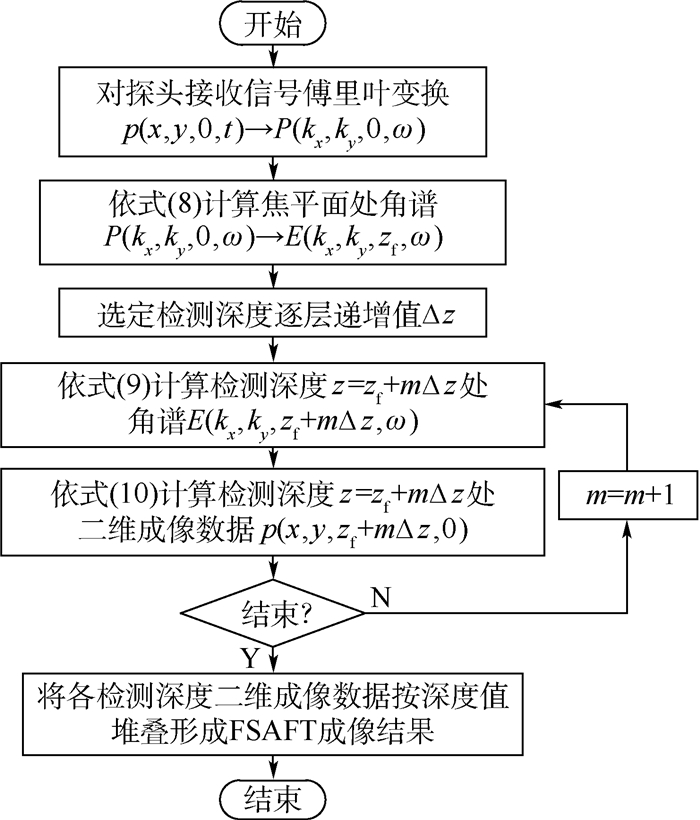 |
| 图 2 点聚焦探头水浸超声检测FSAFT成像流程图 Fig. 2 Flowchart of FSAFT imaging for immersion ultrasonic testing with spherically focused transducer |
| 图选项 |
2 检测图像频域插值算法 超声C扫描图像是二维图像,图像的分辨率取决于扫描步距。扫描步距增大时,检测图像分辨率降低,缺陷边缘判别难度增大。在扫描步距固定时,运用图像插值技术可提高检测图像的分辨率,降低缺陷边缘判别难度。与直接对检测图像进行插值不同,FSAFT成像可使用频域插值算法实现快速图像插值[15]。令S为角谱各频率分量之和,则
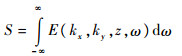 | (11) |
则式(10)等价于
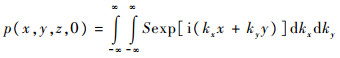 | (12) |
即对角谱各频率分量之和S进行二维傅里叶逆变换。
同一检测深度z的所有S构成的二维图像的频谱A。设插值前A为M行N列的复矩阵,对应的图像点数为M行N列。若将A扩充为rM行rN列(r为大于1的插值系数)的矩阵B,扩充时高频频谱系数补零,则二维傅里叶逆变换后对应的图像点数为rM行rN列。插值后图像点数增加,从而实现对检测图像的插值,插值效果与扫描步距减小为实际扫描步距的1/r相似,即等效扫描步距减小为实际扫描步距的1/r。
3 试验研究与结果分析 3.1 试样与检测参数 试样尺寸图如图 3所示。图 3(a)为钢质材料的试样1,内含直径1.5 mm的横通孔,试样厚度为25 mm。图 3(b)为圆柱形铝材的试样2,内含直径3.2 mm的平底孔。采用点聚焦探头分别对试样1与试样2进行C扫描检测并存储A波数据。探头中心频率为5 MHz,晶片直径为9.5 mm,焦距为45.0 mm,焦斑直径[16]为2.2 mm,与工件表面距离保持为50.5 mm,A波数据采样频率为60 MHz。
 |
| 图 3 试样尺寸图 Fig. 3 Contour dimensional drawing of specimens |
| 图选项 |
3.2 横通孔试样检测结果及分析 扫描步距为0.50 mm时试样1的C扫描图像如图 4所示。根据C扫描图像能较清楚地分辨距试样上表面较近的前7个横通孔,更深处的5个横通孔难以分辨。C扫描图像在y=17.5 mm处的幅值图如图 5所示。所有C扫描图和B扫描图中的幅值均表示超声探伤仪测得的电压值。根据图 5可知,不能直接运用半波高法对缺陷数量和缺陷大小进行定量评价。试样1的B扫描图像如图 6所示,受聚焦探头声场特性的影响,随着检测深度的增加,声场能量分散,检测图像横向分辨率降低,缺陷辨识难度增大。
 |
| 图 4 试样1的C扫描图像 Fig. 4 C-scan image of Specimen 1 |
| 图选项 |
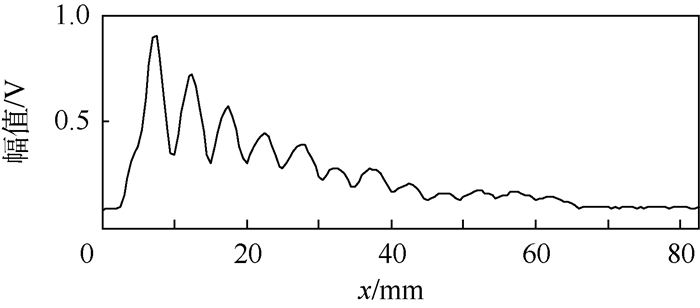 |
| 图 5 试样1的C扫描图像在y=17.5 mm处幅值图 Fig. 5 Amplitude profile of C-scan image of Specimen 1 at y=17.5 mm |
| 图选项 |
 |
| 图 6 试样1的B扫描图像 Fig. 6 B-scan image of Specimen 1 |
| 图选项 |
运用FSAFT对试样1检测数据进行成像,得到C扫描图像如图 7所示,检测图像横向分辨率明显提高,能清晰地分辨出所有横通孔。此时C扫描图像在y=17.5 mm处幅值图如图 8所示,横通孔之间声压变化明显,能运用半波高法对缺陷数量和缺陷大小进行定量评价。分别在y值为5.5~17.5 mm范围内每隔2 mm取一幅C扫描幅值图,分别运用半波高法进行缺陷尺寸定量并取平均值,结果如表 1所示。根据表 1结果可知,FSAFT-DQM缺陷定量误差整体上不随检测深度增加而增加,受检测深度的影响不明显。
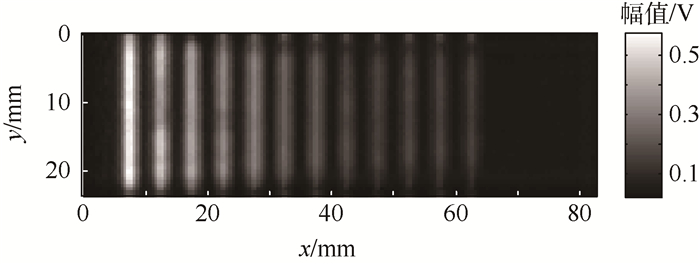 |
| 图 7 试样1 FSAFT成像C扫描图像 Fig. 7 C-scan image of Specimen 1 with FSAFT imaging |
| 图选项 |
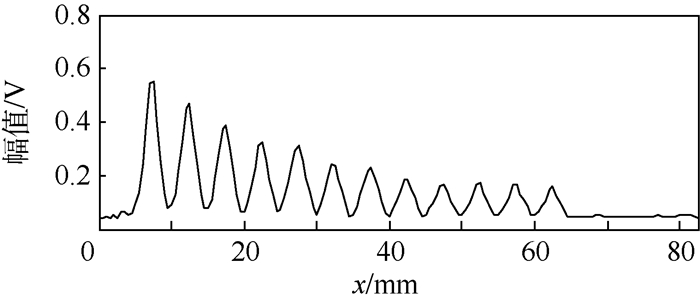 |
| 图 8 试样1 FSAFT成像C扫描图在y=17.5 mm处幅值图 Fig. 8 Amplitude profile of C-scan image of Specimen 1 at y=17.5 mm with FSAFT imaging |
| 图选项 |
表 1 试样1缺陷尺寸半波高法定量结果 Table 1 Quantitative results of defect size of Specimen 1 evaluated with 6 dB drop method
| 孔编号 | 尺寸/mm | 相对误差/% | |
| 实际 | 测量 | ||
| 1 | 1.5 | 2.00 | 33.3 |
| 2 | 1.5 | 2.00 | 33.3 |
| 3 | 1.5 | 2.00 | 33.3 |
| 4 | 1.5 | 2.21 | 47.6 |
| 5 | 1.5 | 2.50 | 66.7 |
| 6 | 1.5 | 2.07 | 38.1 |
| 7 | 1.5 | 2.50 | 66.7 |
| 8 | 1.5 | 2.07 | 38.1 |
| 9 | 1.5 | 2.43 | 61.9 |
| 10 | 1.5 | 2.14 | 42.9 |
| 11 | 1.5 | 2.00 | 33.3 |
| 12 | 1.5 | 1.64 | 9.5 |
表选项
运用FSAFT后试样1的B扫描图像如图 9所示。对比图 6和图 9,FSAFT有效地提高了B扫描图像质量,FSAFT成像结果更清晰,高幅值区域集中在缺陷位置处,不同缺陷之间易于分辨。以图 9左上角的横通孔为基准,以图像中幅值最大位置作为缺陷位置判别依据,各缺陷的位置定量结果如表 2所示。根据表 2结果可知,最大的缺陷位置定量误差不超过0.5 mm,应用FSAFT后缺陷位置定量精度高。
 |
| 图 9 试样1 FSAFT成像B扫描图像 Fig. 9 B-scan image of Specimen 1 with FSAFT imaging |
| 图选项 |
表 2 试样1缺陷位置定量结果 Table 2 Quantitative results of defect position of Specimen 1
| 孔编号 | 定位结果/mm | 定位误差/mm | |||
| x方向 | 检测深度方向 | x方向 | 检测深度方向 | ||
| 1 | 7.5 | 9.2 | 0 | 0 | |
| 2 | 12.5 | 11.8 | 0 | 0.1 | |
| 3 | 17.5 | 13.9 | 0 | -0.3 | |
| 4 | 22.5 | 16.7 | 0 | 0 | |
| 5 | 27.5 | 19.0 | 0 | -0.2 | |
| 6 | 32.0 | 21.6 | -0.5 | -0.5 | |
| 7 | 37.5 | 24.1 | 0 | 0 | |
| 8 | 42.5 | 26.6 | 0 | -0.5 | |
| 9 | 47.5 | 29.0 | 0 | 0 | |
| 10 | 52.5 | 31.6 | 0 | -0.5 | |
| 11 | 57.5 | 34.1 | 0 | 0 | |
| 12 | 62.5 | 36.5 | 0 | -0.5 | |
表选项
3.3 平底孔试样检测结果及分析 图 10为试样2的C扫描图像。图 10(a)为扫描步距等于0.25 mm时试样2的C扫描图像;图 10(b)为FSAFT成像C扫描图像,与图 10(a)对比可知,缺陷回波能量在缺陷位置处更集中。
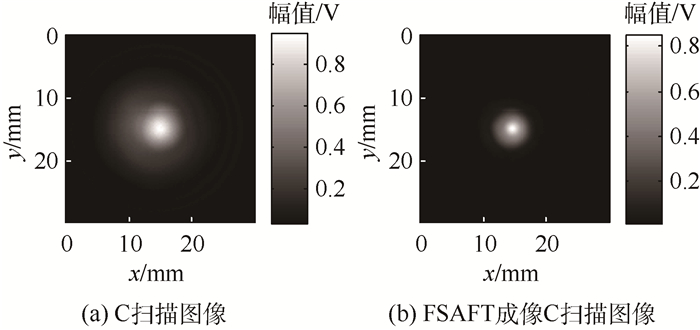 |
| 图 10 试样2的C扫描图像 Fig. 10 C-scan image of Specimen 2 |
| 图选项 |
图 11所示为试样2的B扫描图像和FSAFT成像B扫描图像。FSAFT成像提高了B扫描图像质量,缺陷回波能量更集中。如图 12所示,对比FSAFT成像C扫描图像在x=14.75 mm处的幅值图与原始C扫描图像在同一位置处的幅值图可得出与图 11相同的结果。
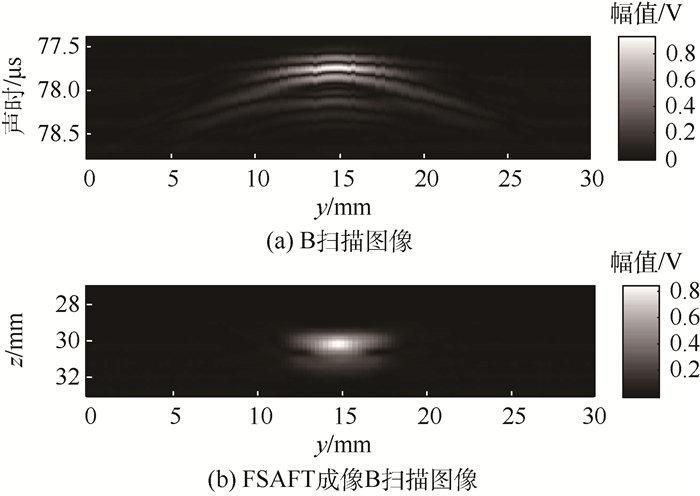 |
| 图 11 试样2的B扫描图像 Fig. 11 B-scan image of Specimen 2 |
| 图选项 |
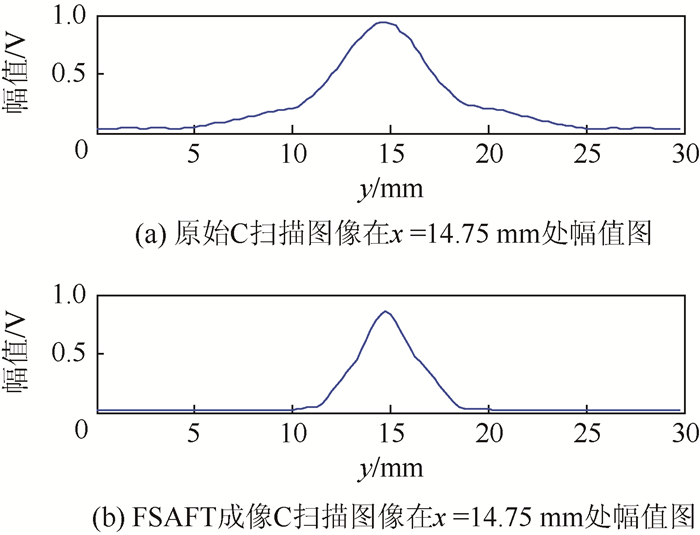 |
| 图 12 试样2的C扫描图像在x=14.75 mm处幅值图 Fig. 12 Amplitude profile of C-scan image of Specimen 2 at x=14.75 mm |
| 图选项 |
当扫描步距为0.25,0.50,0.75,1.25或1.50 mm时,分别取C扫描图像通过缺陷中心位置处x方向和y方向幅值图,运用半波高法进行缺陷定量并取平均值,得出缺陷尺寸定量结果与扫描步距间的关系如表 3所示。
表 3 试样2缺陷尺寸半波高法定量结果 Table 3 Quantitative results of defect size of Specimen 2 evaluated with 6 dB drop method
| 扫描步距/ mm | 实际尺寸/ mm | 未运用FSAFT | 运用FSAFT | |||
| 测量 尺寸/mm | 相对 误差/% | 测量 尺寸/mm | 相对 误差/% | |||
| 0.25 | 3.2 | 5.50 | 71.9 | 3.38 | 5.6 | |
| 0.50 | 3.2 | 5.50 | 71.9 | 3.50 | 9.4 | |
| 0.75 | 3.2 | 5.63 | 75.9 | 3.75 | 17.2 | |
| 1.25 | 3.2 | 5.63 | 75.9 | 3.75 | 17.2 | |
| 1.50 | 3.2 | 5.25 | 64.1 | 4.50 | 40.6 | |
表选项
根据表 3可知,扫描步距为0.25 mm时,直接对检测结果运用半波高法进行缺陷定量评价的定量误差为71.9%,FSAFT-DQM定量误差为5.6%,大幅提高了缺陷定量精度。扫描步距从0.25 mm逐渐增大至1.50 mm时,FSAFT-DQM定量误差从5.6%增大至40.6%,缺陷定量精度整体上随扫描步距增大而变差。
根据空间采样定律,扫描步距越小,采集的超声检测数据越完备,FSAFT成像改善检测图像质量的效果越好,缺陷定量精度越高。但扫描步距每减小1/2时,同一扫描区域内的扫描点数增加为原来的4倍,检测扫查时间和FSAFT运算时间大幅增加,因此需要合理选择扫描步距。超声检测可检的最小缺陷尺寸近似为探头中心频率对应的半波长,运用FSAFT时可依此选择扫描步距[15]。探头中心频率5 MHz对应的半波长为0.63 mm,表 3中扫描步距不大于此值时平底孔缺陷定量误差在10.0%以内。为提高检测效率,扫描步距可适当增大,但不应超过探头中心频率对应的波长,否则定量误差迅速增大。表 3中1.50 mm扫描步距大于探头中心频率对应的波长,此时缺陷定量误差达到40.6%,对定量精度的改善作用大幅降低。
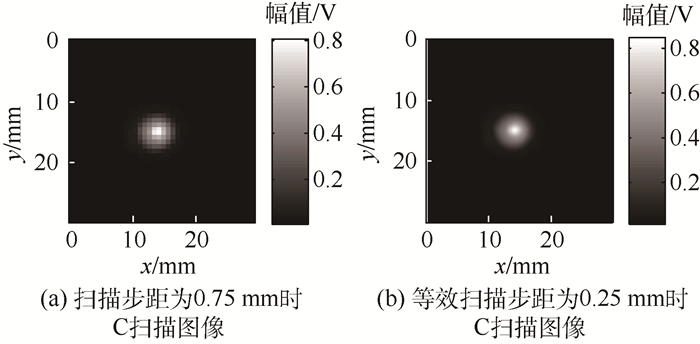
扫描步距增大时,检测效率提高,但检测图像质量下降,缺陷定量精度降低。在扫描步距为探头中心频率对应的半波长和波长之间时,运用图像频域插值算法可提高检测图像质量,更易识别缺陷边缘。扫描步距为0.75 mm时FSAFT成像C扫描图像如图 13(a)所示。对图 13(a)进行频域插值,插值系数为3,插值后图像如图 13(b)所示,检测图像分辨率得到提高,缺陷边缘更清晰。此外,频域插值图像等效扫描步距减小,能降低扫描步距对缺陷定量结果的影响。
 |
| 图 13 试样2 FSAFT成像C扫描图像和频域插值图像 Fig. 13 C-scan image of specimen 2 with FSAFT imaging and image with frequency domain interpolation |
| 图选项 |
对图 13(a)采用不同的插值系数插值得出一组C扫描图像,分别取通过缺陷中心位置处x方向和y方向的幅值图用半波高法进行缺陷大小定量并取平均值,得出缺陷尺寸与等效扫描步距间的关系如表 4所示。随着等效扫描步距的减小,缺陷定量误差整体上从17.2%减小到5.6%并维持稳定,小幅提高了平底孔缺陷定量精度。
表 4 试样2频域插值图像缺陷尺寸定量结果 Table 4 Quantitative results of defect size of specimen 2 with frequency domain interpolated image
| 等效扫描步距/mm | 缺陷尺寸/mm | 相对误差/% | |
| 实际 | 测量 | ||
| 0.750 | 3.2 | 3.75 | 17.2 |
| 0.375 | 3.2 | 3.38 | 5.6 |
| 0.250 | 3.2 | 3.50 | 9.4 |
| 0.186 | 3.2 | 3.47 | 8.4 |
| 0.150 | 3.2 | 3.45 | 7.8 |
| 0.125 | 3.2 | 3.38 | 5.6 |
| 0.107 | 3.2 | 3.38 | 5.6 |
| 0.093 | 3.2 | 3.38 | 5.6 |
表选项
4 讨论 在扫描步距为0.50 mm时,表 1中横通孔试样FSAFT-DQM缺陷定量误差整体上比平底孔试样缺陷定量误差大。这是由于横通孔对声波的散射规律不同于平底孔,横通孔散射角度更大、反射回波能量更分散所导致。表 1中的数据重在分析检测深度对缺陷定量误差变化情况的影响,对缺陷定量误差的绝对大小的影响在其次。
FSAFT可用于平探头和聚焦探头检测,应用于聚焦探头时需进行修正。该技术只能用于脉冲反射法检测试样内部缺陷,对缺陷形状、尺寸并没有要求。该技术以探头接收到的信号作为波动方程求解的边界条件、采用逐层递推的方式求解试样内部声场,这一特点使其不仅能用于均一材料,也能用于层状材料。
5 结论 1) FSAFT能有效提高检测图像横向分辨率,在能接收到有效缺陷回波的检测深度范围内,FSAFT-DQM缺陷定量精度基本不变。
2) FSAFT能有效降低与点聚焦探头焦斑尺寸相近缺陷的半波高法定量误差,克服了半波高法对小于声束直径的缺陷定量时误差较大的问题,扩展了半波高法的应用范围。
3)为保证缺陷定量精度,一般可以探头中心频率对应的半波长作为扫描步距。扫描步距在半波长到波长之间时,运用图像频域插值算法可提高检测图像分辨率,小幅降低缺陷定量误差。扫描步距大于波长时,缺陷定量误差迅速增大。
参考文献
| [1] | THOMPSON R B. Quantitative ultrasonic nondestructive evaluation methods[J].Journal of Applied Mechanics, 1983, 50(4b): 1191–1201.DOI:10.1115/1.3167201 |
| [2] | 郑中兴. 第四专题超声检测中缺陷的定量[J].无损检测, 1994, 16(2): 52–57.ZHENG Z X. Quantitative evaluation of flaws in ultrasonic testing[J].Nondestructive Testing, 1994, 16(2): 52–57.(in Chinese) |
| [3] | 史亦韦. 超声检测[M].北京: 机械工程出版社, 2005: 119-126.SHI Y W. Ultrasonic testing[M].Beijing: China Machine Press, 2005: 119-126.(in Chinese) |
| [4] | SILK M G. Defect detection and sizing in metals using ultrasound[J].International Materials Reviews, 1982, 27(1): 28–50.DOI:10.1179/imr.1982.27.1.28 |
| [5] | 胡宏伟, 彭凌兴, 周正干, 等. 曲面构件水浸超声检测缺陷定量研究[J].航空学报, 2014, 35(11): 3166–3173.HU H W, PENG L X, ZHOU Z G, et al. Quantitative research on defect of curved components with immersion ultrasonic testing[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 3166–3173.(in Chinese) |
| [6] | 王铮, 梁菁, 史丽军, 等. 复合材料层板超声检测缺陷评定方法分析[J].南京航空航天大学学报, 2012, 44(S): 138–141.WANG Z, LIANG J, SHI L J, et al. Measurement for ultrasonic contact inspection on defect in carbon fiber-reinforced composite[J].Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(S): 138–141.(in Chinese) |
| [7] | SCHMERR L W. Fundamental of ultrasonic nondestructive evaluation[M].New York: Plenum Press, 1998: 181-197. |
| [8] | BUSSE L J, COLLINS H D, DOCTOR S R.Review and discussion of the development of synthetic aperture focusing technique for ultrasonic testing (SAFT-UT):NUREG/CR-3625[R].Richland:Pacific Northwest Lab, 1984. |
| [9] | FREDERICK J R, SEYDEL J A, FAIRCHILD R C.Improved ultrasonic non-destructive testing of pressure vessels:NUREG-O007-1[R].Ann Arbor:University of Michigan, 1976. |
| [10] | BUSSE L J. Three-dimensional imaging using a frequency-domain synthetic aperture focusing technique[J].IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1992, 39(2): 174–179.DOI:10.1109/58.139112 |
| [11] | STEPINSKI T. An implementation of synthetic aperture focusing technique in frequency domain[J].IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2007, 54(7): 1399–1408.DOI:10.1109/TUFFC.2007.400 |
| [12] | 吴施伟, 吴海腾, 金浩然, 等. 聚焦探头水浸检测下的频域合成孔径聚焦技术[J].浙江大学学报(工学版), 2015, 49(1): 110–115.WU S W, WU H T, JIN H R, et al. Frequency-domain synthetic aperture focusing technique for immersion testing using focused transducer[J].Journal of Zhejiang University (Engineering Science), 2015, 49(1): 110–115.(in Chinese) |
| [13] | ROSE J L. Ultrasonic waves in solid media[M].Cambridge: Cambridge University Press, 2004: 24-26. |
| [14] | GOODMAN J W. Introduction to Fourier optics[M].New York: McGraw-Hill, 1996: 55-58. |
| [15] | LEVESQUE D, BLOUIN A, NERON C, et al. Performance of laser-ultrasonic F-SAFT imaging[J].Ultrasonics, 2002, 40(10): 1057–1063.DOI:10.1016/S0041-624X(02)00256-1 |
| [16] | SCHMERR L W, SONG S J. Ultrasonic nondestructive evaluation system:Models and measurements[M].New York: Springer Science & Business Media, 2007: 152-153. |
