发动机的涡轮部件工作环境十分恶劣,积垢、氧化、侵蚀等多重效应的作用[3]可能使涡轮叶片表面的粗糙度达到“过渡粗糙”或者“完全粗糙”数量级[4],其影响主要体现在2个方面[5]:一方面,能改变湍流边界层的阻力系数和传热系数,直接影响气动及传热特性;另一方面,壁面粗糙度可能对边界层的流动状态,如层流到湍流的转捩、流动分离等产生影响,间接影响叶片的传热特性。
Taylor[6]利用表面光度仪对航空发动机涡轮叶片进行测量,认为典型的粗糙高度为1~12 μm。Bons等[7]对近100个使用期内的不同尺寸的涡轮部件进行研究,指出在叶片中截面处的平均粗糙高度可达到37 μm。Barlow[8]和Hosni[9]等对平板的传热性能进行实验研究,结果表明特定的表面粗糙度使平板热传导系数增加了120%。Abuaf等[10]的实验发现随着表面粗糙度的增加,转捩发生的更早并且湍流边界层具有更高的热传导系数。Bunker[11]研究了最大粗糙高度为27.8 μm的跨声速叶栅流动,结果表明与自由流湍流度相比,表面粗糙度对转捩的影响占主导作用。Boyle等[12]和Blair[13]也对粗糙壁面的涡轮叶栅进行了研究。
表面粗糙度对边界层转捩有重要影响,模拟粗糙壁面的流动首先要准确预测转捩,这对数值模拟方法提出了新的挑战。与实验研究相比,已公开发表的数值模拟方面的研究成果相对较少。Stripf等[14-15]做出开创性工作,提出基于粗糙单元高度的转捩起始位置经验公式,并结合离散单元粗糙度(discrete element roughness)模型[16-17]与双层k-ε(two layer k-ε)模型(k为湍动能,ε为湍动能耗散率), 模拟了粗糙壁面的边界层转捩。Boyle和Stripf[18]针对不同的粗糙单元的几何形状提出一种新的表面等效沙粒粗糙度计算方法,并利用涡轮叶栅的实验结果进行了验证。Lorenz等[19]基于Stripf[14-15]的工作改进了粗糙度准则公式,使结果与实验值符合得更好。另一方面,Hellsten和Seppo[20]、Aupoix[21]以及Bellucci等[22]对基于k-ω Shear Stress Transport(SST)两方程模型的壁面粗糙度修正法进行研究,但这些方法不能对边界层转捩进行有效预测。
本文在Hellsten和Seppo[20]及Stripf等[14]工作的基础上,提出了针对γ-Reθ转捩模型[23]的表面粗糙度修正方法(γ为间歇因子,Reθ为边界层的转捩动量厚度雷诺数):一方面,采用新的适用于粗糙表面的边界条件,以模拟粗糙表面对湍流边界层的影响;另一方面,改进模型中的经验关联函数,使模型适用于预测粗糙表面流动的转捩预测。利用粗糙平板的风洞试验数据和某低压涡轮叶栅实验数据对模型进行验证,并用该模型对粗糙壁面的Mark Ⅱ涡轮叶栅的流动进行数值模拟,研究粗糙度对边界层转捩及壁面传热特性的影响。
1 数值方法 1.1 γ-Reθ转捩模型 γ-Reθ转捩模型由Langtry和Menter[23]提出,该模型有两个输运方程,分别是转捩起始位置的边界层动量厚度雷诺数(


 | (1) |
式中:ρ为密度;t为时间;Uj和xj分别为张量表示的速度分量和坐标分量;Pθt为源项,详细表达式参见文献[23];μ为层流涡黏性系数;σθt=2.0为常数。
Pθt作用是使边界层外的


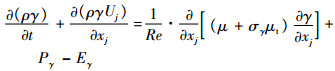 | (2) |
式中:Pγ为控制间歇因子增长的源项;σγ=1.0为常数;Eγ为破坏项,详细的表达式参见文献[23]。
通过式(1)和式(2)两个输运方程,可以得到流场中间歇因子的分布,还需要与湍流模型相结合才能模拟转捩过程。Langtry和Menter推荐k-ω SST模型,即用间歇因子来修正湍动能k的输运方程的生成项、破坏项和混合函数[23-24]。
1.2 表面粗糙度修正方法 一方面,为了考虑表面粗糙度对湍流边界层的影响,Hellsten和Seppo[20]提出了对k-ω SST模型的粗糙度修正方法。通过对壁面处湍动能k和比耗散率ω的修正来模拟粗糙度的影响,具体方法如下:
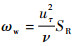 | (3) |
式中:ωw为壁面位置的湍动能比耗散率;uτ=
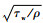
 | (4) |
式中:ks+为无量纲的表面沙粒粗糙度,其定义为
 | (5) |
式中:ks为表面等效沙粒粗糙度,以下简称为表面粗糙度。
为准确模拟边界层内的流动,还需要在k-ω SST模型的涡黏性表达式中增加一个掺混函数F3,具体表达式参见文献[20]。
另一方面,为考虑表面粗糙度对边界层转捩位置的影响,Stripf等[14, 25]重新定义了一个粗糙表面的转捩动量厚度雷诺数Reθt_Rough,该变量与等效沙粒粗糙度ks和边界层的位移厚度δ*有关,其表达式为
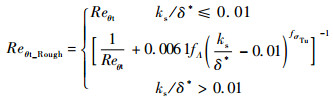 | (6) |
式中:函数fΛ用于描述粗糙单元几何结构,即形状、排列规律等的影响,而本文未考虑这些影响因素,令fΛ=1;fσTu为当地自由流湍流的函数,其定义为
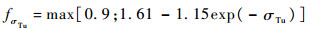 | (7) |
式中:σTu为当地湍流度。
1.3 考虑粗糙度影响的转捩模型 首先,模型要考虑表面粗糙度对湍流边界层的影响,表面粗糙度会对转捩位置之后的湍流边界层产生直接的影响,如改变边界层内部的湍动能和涡粘性系数。γ-Reθ转捩模型对湍流边界层的计算方法与常规湍流模型是近似一致的,因此Hellsten和Seppo[20]的边界条件修正方法同样适用。本文将该方法引入到γ-Reθ转捩模型中,模拟的边界层转捩点后湍流边界层区域内的阻力系数与Mills-Hang的经验公式[20]符合得很好。
粗糙表面流动转捩预测的另一个重要问题就是模拟表面粗糙度对转捩位置的影响。原始γ-Reθ模型中的经验关联公式均是基于光滑平板低速绕流实验数据拟合得到的,而其中最为重要的是起始位置边界层转捩动量厚度雷诺数与当地湍流度、速度梯度、压力梯度等的经验关联公式。考虑表面粗糙度的影响,对该公式进行改写,使模型具备预测粗糙表面流动转捩的预测能力是可行的。
Stripf等[14]提出的经验公式已经给出了一个基于实验数据拟合得到的转捩动量厚度雷诺数与表面等效沙粒粗糙度的关系式(式(6)和式(7)),但该关系式与γ-Reθ转捩模型中的经验关联公式不同,式(6)中的边界层位移厚度和转捩动量厚度是全局变量,进行数值模拟时需要进行积分求解。为克服这个问题,本文引入流场当地位移厚度,重新建立形如式(6)和式(7)的表达式,并与γ-Reθ转捩模型中的输运方程相结合,进而得到粗糙表面转捩动量厚度雷数Reθt_Rough的分布,值得注意的是,这里的δ*与Reθt均为流中的当地变量,与Stripf等[14]的公式中的变量含义不同。下面介绍当地变量位移厚度δ*的计算方法,γ-Reθ模型的公式中转捩动量厚度需要进行迭代求解,将Reθt的定义式(8)带入经验关联式(9),可见等号两端均含有转捩动量厚度θt,需要通过简单的迭代方法进行求解。
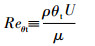 | (8) |
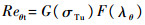 | (9) |
式中:U为流场当地速度;G(σTu)和F(λθ)为γ-Reθ模型中的公式,具体表达式参见文献[23]。
得到流场中转捩动量厚度θt后,需要估算出位移厚度δ*,本文通过算例验证,采用了计算简便的湍流边界层速度剖面的N次方定律[26]来求解。
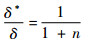 | (10) |
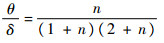 | (11) |
式中:θ为边界层动量厚度,δ为边界层厚度,n取为7。得到边界层位移厚度δ*之后,结合公式(6)即可得到流场中Reθt_Rough的分布。
Langtry和Menter[23]的γ-Reθ转捩模型以及上述修正方法在自行开发的CFD程序HGFS上实现,程序的介绍及应用情况可参见文献[27-30]。
2 模型的验证 首先,参照Wang[31]和Pinson[32]等的风洞试验数据,对粗糙平板的转捩流动进行验证。分别选择了光滑壁面以及表面等效沙粒粗糙度ks分别为150 μm和400 μm,来流湍流度σTu∞在0.5%~5.2%的工况进行数值模拟,如表 1所示。
表 1 粗糙平板算例的计算参数 Table 1 Calculation parameters for rough flat plate cases
| 算例 | U∞/(m·s-1) | Re∞/(105m) | σTu∞/% | ks/μm |
| 1S | 8.6 | 5.8 | 0.5 | (光滑) |
| 2R | 8.6 | 3.1 | 0.5 | 150 |
| 3R | 7.0 | 3.1 | 1.4 | 400 |
| 4R | 4.6 | 3.1 | 5.2 | 400 |
| 注:S,R—光滑壁面、粗糙壁面的算例;U∞—来流速度;Re∞—来流雷诺数。 | ||||
表选项
湍流边界层热传导系数一般远高于层流边界层,因此传热特性曲线可以明显地反映出转捩位置,计算得到的Stanton数与实验值的对比如图 1所示,图中横坐标Rex表示当地位置的雷诺数,曲线表示数值模拟的结果,空心三角符号表示光滑表面的实验结果,实心符号(圆点、正方形、菱形)表示相对应的粗糙表面的实验结果。可以看出对于不同表面粗糙度和来流湍流度的情况,本文模型所预测的转捩位置均与实验值符合得很好,但在较高表面粗糙度情况下,如ks=400 μm,预测的转捩区长度比实验结果稍短。
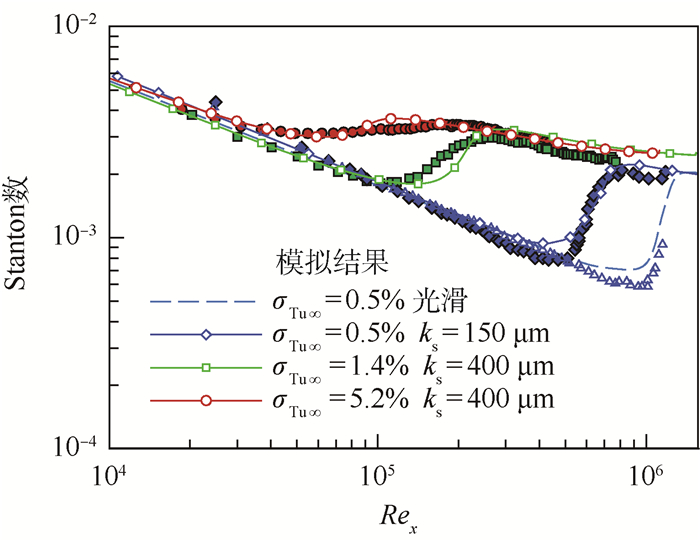 |
| 图 1 粗糙平板传热系数与实验值的对比 Fig. 1 Comparison between heat transfer coefficient on rough flat plate and experimental data |
| 图选项 |
其次,为验证本文的方法与模型在复杂流动情况中的适用性,选择某高压涡轮导叶(HPTV)算例进行验证,对应的实验由德国Karlsruhe大学[33]完成。弦长c=93.95 mm,来流雷诺数Re∞=1.4×105,来流湍流度σTu∞=3.5%。不同表面粗糙度参数如表 2所示。
表 2 HPTV算例的表面粗糙度参数 Table 2 Surface roughness parameters for HPTV case
| 粗糙表面算例 | ks/μm |
| 光滑表面 | 0 |
| HPTV_20a | 72 |
| HPTV_40b | 129 |
| HPTV_70 | 238 |
| 注:HPTV_20a,HPTV_40b,HPTV_70—粗糙表面实验工况代号。 | |
表选项
计算采用如图 2所示二维非结构网格,单元总数为24 000,壁面附近进行加密处理,保证最大y+ < 0.8,从局部视图来看,前缘和尾缘均有较高的网格分辨率,经过网格无关性验证,此网格满足计算要求。
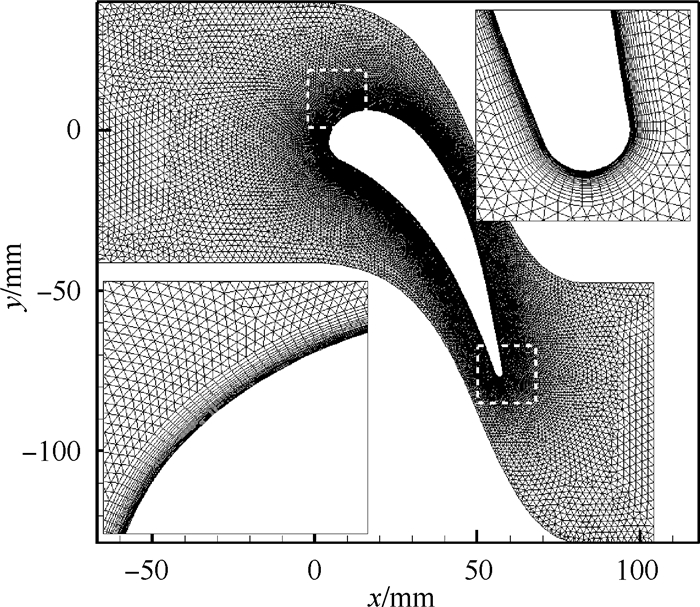 |
| 图 2 HPTV算例的网格 Fig. 2 Computational grid for HPTV case |
| 图选项 |
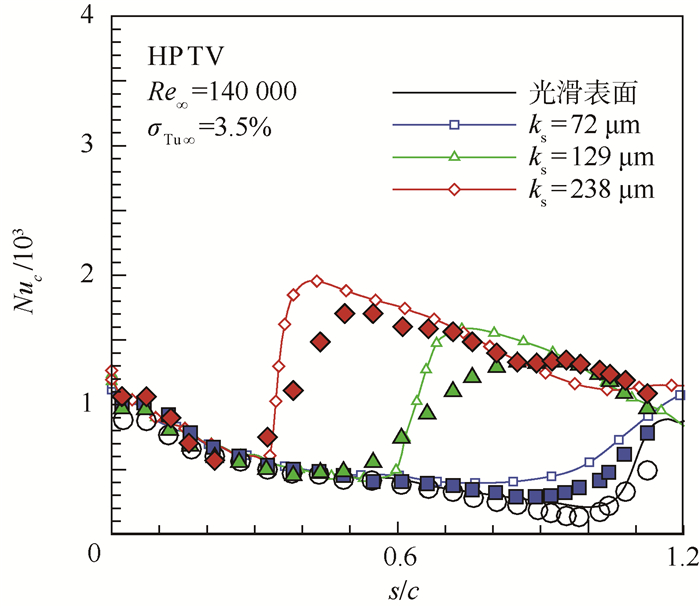
图 3是数值模拟的HPTV叶片表面传热特性曲线与实验值的对比,s为吸弧长(图中所示为叶片吸力面),Nuc为努赛尔数,其定义为
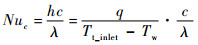 | (12) |
式中:λ为恒定的热传导系数[33],本算例中λ=0.03 W/(m·K);Tt_inlet为进口总温;Tw为叶片表面温度。图 3中带标记的实线表示不同表面粗糙度条件下的计算结果,而相应的实心符号则表示该条件下的实验结果。从图 3中可以看出本文模型预测的Nuc幅值与变化规律与实验符合得很好;对光滑壁面的转捩预测比较准确,对于ks=72 μm的工况预测的转捩位置与转捩区长度也与实验结果接近;ks=129,238 μm的粗糙度下,预测的转捩位置与实验值接近,但转捩区长度较短,与实验值有一定差别。总体来看,本文模型对涡轮叶栅中表面粗糙度诱导的边界层转捩流动有较为理想的预测精度。
 |
| 图 3 粗糙表面涡轮叶片的传热系数 Fig. 3 Heat transfer coefficient of turbine vane with rough surface |
| 图选项 |
3 计算结果与分析 利用本文模型对内冷涡轮导叶Mark Ⅱ的5411工况[34]进行流/热耦合数值模拟,研究粗糙壁面对其流动及传热性能的影响。
3.1 光滑壁面条件下的验证 HGFS程序中流/热耦合计算处理方法为流体域、固体域分别求解,在边界进行信息耦合,Mark Ⅱ涡轮导叶是验证流/热耦合计算程序的经典算例,其5411工况主要进出口边界条件如表 3所示。
表 3 Mark Ⅱ导叶5411工况的边界条件 Table 3 No.5411 boundary condition of Mark Ⅱ turbine vane
| Tt_inlet/K | pt_inlet/Pa | σTu_inlet/% | poutlet/Pa |
| 788 | 337 000 | 6.5 | 169 850 |
| 注:pt_inlet—进口总压;σTu_inlet—进口湍流度;poutlet—出口静压。 | |||
表选项
计算采用图 4所示的二维非结构网格,其中流体域单元总数为87 000,计算得到的y+在0.4~0.9范围内,固体域单元总数为12 000。
 |
| 图 4 Mark Ⅱ导叶计算网格 Fig. 4 Computational grid for Mark Ⅱ turbine vane |
| 图选项 |
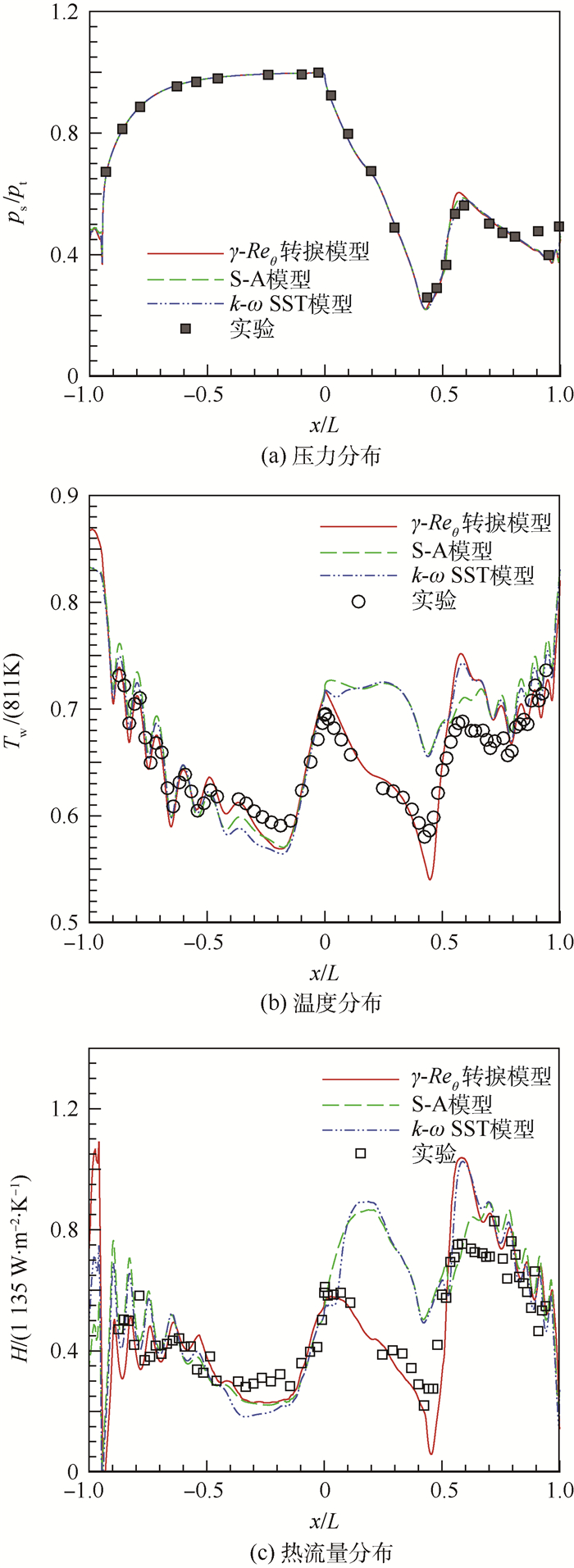
分别利用S-A模型、k-ω SST模型以及γ-Reθ转捩模型对Mark II叶片(光滑壁面)的流动进行数值模拟,计算得到的压力、温度和热流量的分布如图 5(a)~图 5(c)所示。L为轴向弦长,横坐标0代表前缘点,左侧(即x/L < 0的范围)表示吸力面,右侧表示压力面,图 5~图 9均采用相同的表示方法。不同模型计算得到的壁面压力分布近似一致,且均与实验值符合得很好。而温度分布则有较大的差别,主要原因在于S-A与k-ω SST等全湍流模型的结果中转捩是非物理的,且极容易发生,所预测的转捩位置通常远远早于真实情况,从图 5(b)和图 5(c)的结果来看这2个模型模拟的边界层在叶片吸力面几乎从前缘点就已经转捩,导致0~50%轴向弦长(以下简称为弦长)壁面温度偏高。γ-Reθ模型预测的转捩位置与实验结果非常接近,转捩点约在50%弦长位置,转捩点之后的位置有一定的“过调”现象,但壁面的温度和热流量的分布总体与实验值符合得很好。
 |
| 图 5 光滑壁面条件下的验证 Fig. 5 Verification in smooth surface condition |
| 图选项 |
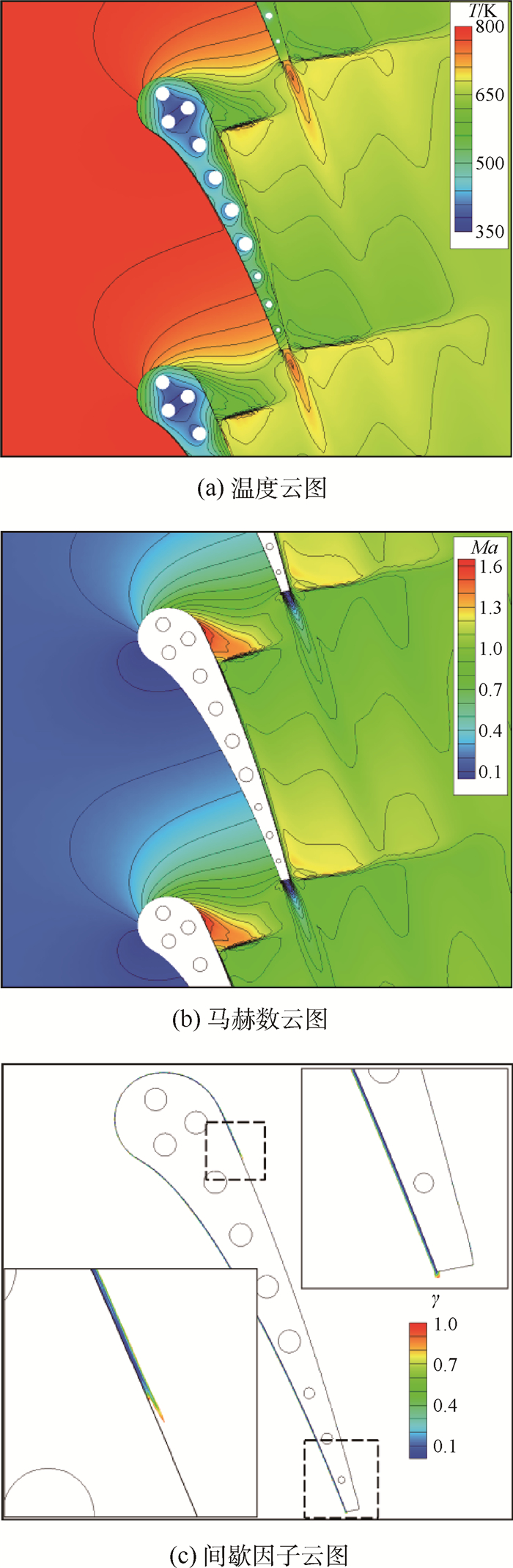
利用γ-Reθ转捩模型数值模拟得到的流场如图 6所示,其中图 6(a)~图 6(c)分别为温度(T)云图、马赫数(Ma)云图以及间歇因子(γ)云图。由于叶片内部马赫数为0,因此图 6(b)中并未示出(以白色背景代替),与之类似,图 6(c)中只显示了流场中边界层内间歇因子的分布,在叶片内部间歇因子为0,而流场广阔区域内该值的分布接近于1。从图 6(a)和图 6(b)中可以清晰看出叶片吸力面的激波,结合图 6(c)间歇因子的分布可以看出,激波位置之前,吸力面边界层为层流流动,激波之后转变为湍流;而压力面边界层始终为层流,只有在尾缘点(方形尾缘)才转变为湍流。
 |
| 图 6 利用γ-Reθ模型数值模拟得到的流场 Fig. 6 Numerical simulated flow field by γ-Reθ model |
| 图选项 |
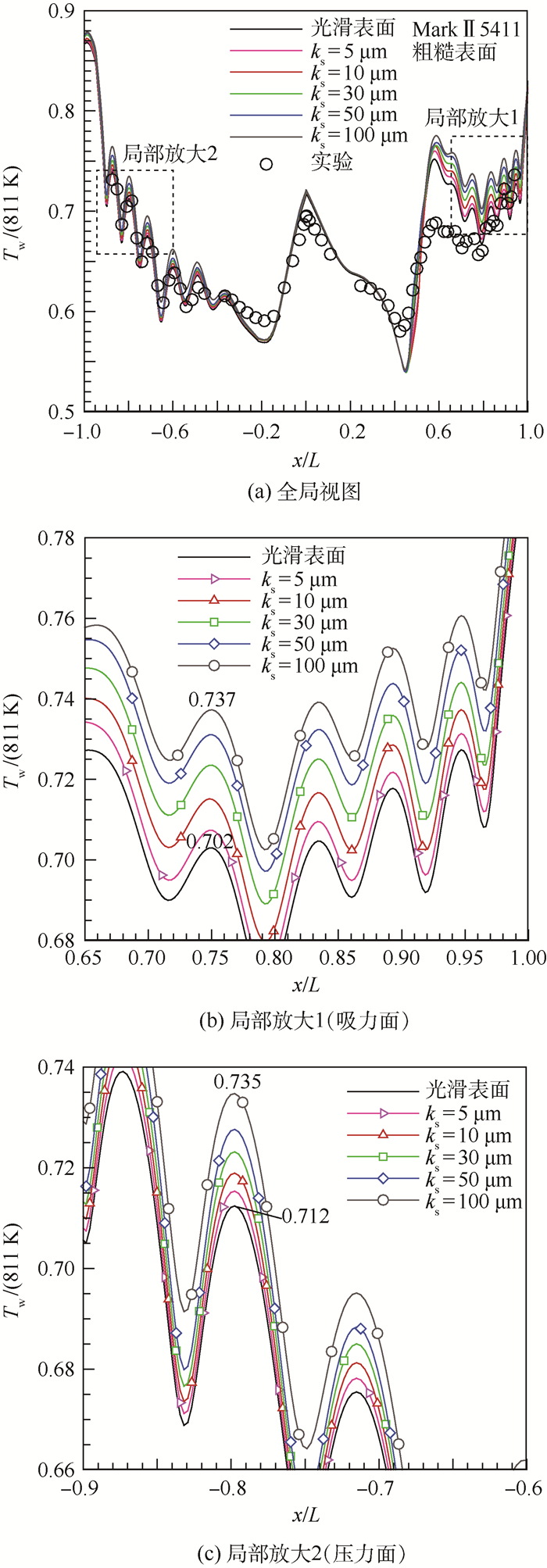
3.2 粗糙壁面对流动及传热的影响 保证其他边界条件与来流参数均与3.1节MarkⅡ5411工况相同,只增加壁面粗糙度的影响,数值模拟的温度分布曲线如图 7所示,图中列出了光滑壁面以及叶片表面粗糙度ks=5~100 μm的计算结果。其中:图 7(a)为全局视图,图 7(b)和图 7(c)分别为吸力面、压力面虚线方框内的局部放大视图。图 8为粗糙度ks=100~175 μm的壁面温度分布,图 9为边界层内间歇因子分布。
 |
| 图 7 不同壁面粗糙度条件下的温度分布(ks=5~100 μm) Fig. 7 Distribution of wall temperature in different surface-roughness conditions (ks=5-100 μm) |
| 图选项 |
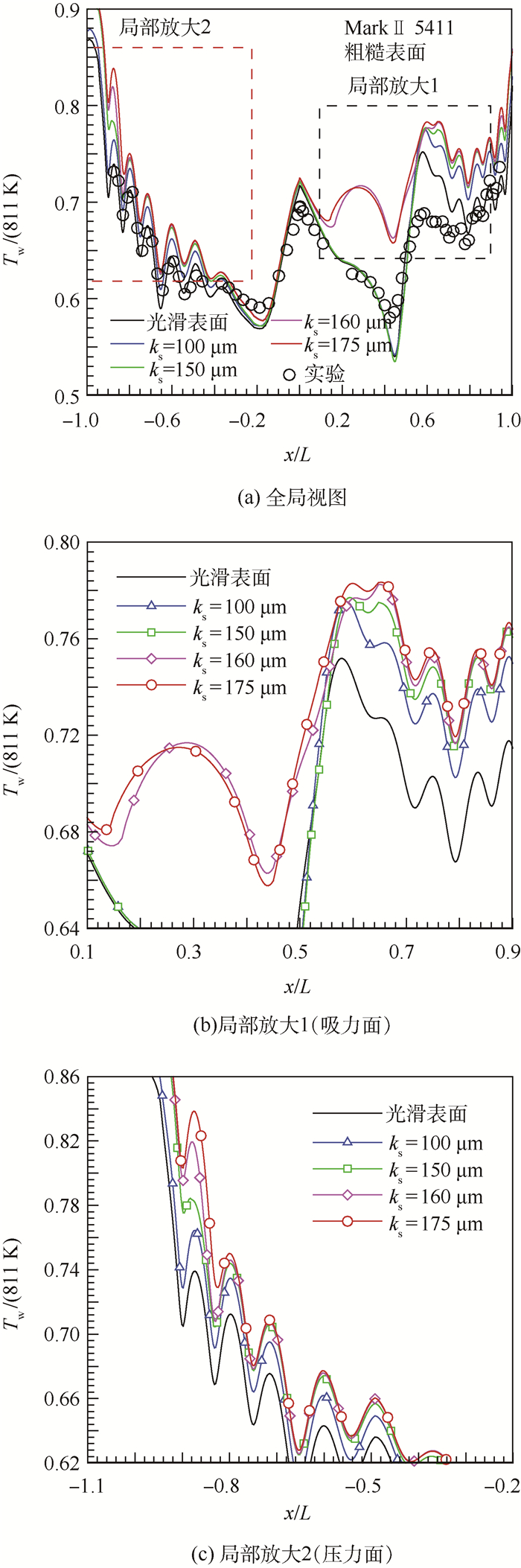 |
| 图 8 不同壁面粗糙度条件下的温度分布(ks=100~175 μm) Fig. 8 Distribution of wall temperature in different surface-roughness conditions (ks=100-175 μm) |
| 图选项 |
从图 7(a)可以看出,在5~100 μm范围内,粗糙度不同的壁面计算得到的温度分布呈现较为一致的规律;压力面0~20%弦长以及吸力面0~50%弦长的温度分布几乎不受粗糙度的影响,压力面20%弦长到尾缘的范围内受到的影响较小,而吸力面50%弦长以后的位置受表面粗糙度影响较大。
从图 7(b)中的温度分布曲线来看,与光滑壁面相比,粗糙度为5 μm的壁面使该区域壁面相对温度,即Tw/(811K)升高了约0.007,绝对温度升高约5.7 K,而粗糙度为100 μm的壁面使相对温度升高约0.035,绝对温度升高28.4 K,增幅约为5%。在图 7(c)中,100 μm的壁面粗糙度使压力面相对温度升高约0.023,绝对温度升高18.7 K,增幅小于吸力面湍流区。从上述结果中可以得到如下结论:
1)随着表面粗糙度的增加,湍流边界层换热效果有较大幅度增强,导致壁面温度升高,而完全层流边界层区域内的壁面温度保持不变,如图中x/L=-0.2~0.5的区间内所示。
2)湍流边界层内,随着表面粗糙度的增加,温度的变化规律并不是线性的,粗糙度越大其影响效果越弱,即随着粗糙度的逐渐增大,温度增加的幅度在逐渐减小,热流量也体现相同的规律。
3)从边界层内间歇因子分布(见图 9)来看,ks=5~100 μm范围内叶片压力面并未发生转捩,边界层为层流,但表面粗糙度对压力面20%弦长到尾缘的区域也有一定影响,说明该区域的边界层呈现出一定的湍流脉动特性。
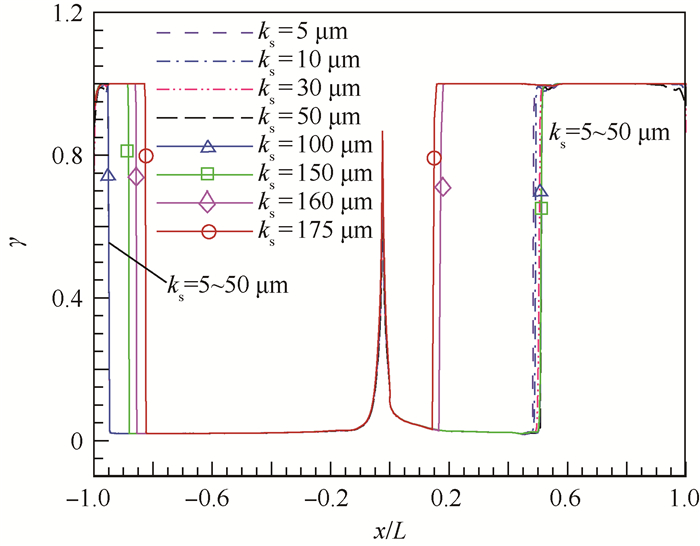 |
| 图 9 边界层内间歇因子分布 Fig. 9 Distribution of intermittency factor in boundary layer |
| 图选项 |
从图 8可以看出ks为100 μm和150 μm时温度曲线仍与图 7有相同的变化规律,即图 8(b)中湍流边界层内壁面温度进一步升高;当ks增加到160 μm时,温度分布曲线出现较大变化,吸力面15%~50%弦长范围内温度大幅增加,由原来的低谷区变成新的峰值区。结合图 9中间歇因子的分布可以看出,ks增加到160 μm时吸力转捩位置由50%弦长处前移到15%弦长附近,转捩位置之后的边界层由层流变为湍流,换热能力的增强使壁面温度显著升高。
图 8(c)中,当ks增加到150 μm以上时,压力面温度分布曲线在80%~90%弦长位置增加幅度较大,从图 9可以看出,较高的壁面粗糙度使压力面边界层也发生了转捩。
边界层内间歇因子的分布如图 9所示,在压力面ks=5~50 μm和ks=100 μm的分布曲线几乎完全重合,图例中ks=5~50 μm的曲线用不同类型的虚线表示,而ks≥100 μm的曲线用带有符号的实线表示。间歇因子的分布能直观地反映出边界层的转捩情况:
1)对于吸力面,ks=5~150 μm范围内,边界层转捩位置均在50%弦长附近;当ks增加到160 μm时,转捩位置前移到15%弦长附近,而当ks继续增加到175 μm时,转捩位置略有提前。
2)对于压力面,ks=5~100 μm范围内,转捩发生在尾缘点,即整个吸力面均为层流流动;当ks增加到150 μm时,转捩位置前移到90%弦长,且当ks继续增到160 μm和175 μm时,转捩位逐渐前移到85%和80%弦长附近。即压力面的转捩首先发生在尾缘,且随着粗糙度的增加转捩位置逐渐前移。
3)对比ks为150、160和175 μm的结果可以看出吸力面转捩位置的变化并不是线性的,与第2节验证算例中HPTV涡轮叶片的结果不同。这是因为Mark Ⅱ吸力面的转捩是由激波边界层干涉的诱导而发生的,当壁面粗糙度较小时,激波对转捩的作用效果为主导,只有当粗糙度大于某临界值时,其较强的影响效果才会使转捩点发生变化,本算例中该临界值近似为150 μm。
4 结论 在内部CFD程序HGFS中对γ-Reθ转捩模型进行改进,使该模型能够预测粗糙壁面的转捩流动。利用本文模型对Mark Ⅱ涡轮导叶的流动进行数值模拟,得到如下结论:
1)随着表面粗糙度的增加,叶片层流边界层换热系数变化不大,而湍流边界层换热系数有较大幅度增加,进而导致壁面温度升高。且随着表面粗糙度的增加,温度和热流量的变化规律并不是线性的,粗糙度越大其影响效果越弱。
2)在叶片吸力面边界层为湍流的区域,与光滑壁面相比,等效沙粒粗糙度为5 μm的壁面使该区域温度升高约5.7 K,而粗糙度为100 μm的壁面使温度升高28.4 K,增幅达5%左右。
3)粗糙度对叶片吸力面转捩位置的影响不是线性的,当粗糙度大于某一临界值时转捩位置发生突变。吸力面边界层转捩是由激波边界层干涉诱导而产生的,当粗糙度较低时(ks < 100 μm),激波的作用效果为主导,只有当粗糙度大于某临界值时才会对转捩产生影响,本算例中该临界值近似为150 μm。
4)光滑壁面以及较低粗糙度(ks < 100 μm)范围内,压力面边界层均为层流,当粗糙度增大到150 μm时,压力面的转捩首先发生在尾缘,且随着粗糙度的增加转捩位置逐渐前移。
本文对γ-Reθ模型的修正方法在一定粗糙度范围内得到了规律比较一致的结果,且预测的温度、热流量、转捩位置等参数的变化趋势与真实流动情况相符,但仍需要更为充分的实验数据对该方法进行验证与完善,这是下一步需要进行的工作。
参考文献
| [1] | BUNKER R S. A review of shaped hole turbine film-cooling technology[J].Journal of Heat Transfer, 2005, 127(4): 441–453.DOI:10.1115/1.1860562 |
| [2] | YEH F C, STEPKA F S.Review and status of heat-transfer technology for internal passages of air-cooled turbine blades:NASA-TP-2232[R].Washington, D.C:NASA, 1984. |
| [3] | 李本威, 李冬, 沈伟, 等. 涡轮叶片粗糙度对其性能衰退的影响研究[J].航空计算技术, 2009, 39(5): 26–29.LI B W, LI D, SHEN W, et al. Research on turbine lamina roughness influence on its performance declination[J].Aeronautical Computing Technique, 2009, 39(5): 26–29.(in Chinese) |
| [4] | BOGARD D G, SCHMIDT D L, TABBITA M. Characterization and laboratory simulation of turbine airfoil surface roughness and associated heat transfer[J].Journal of Turbomachinery, 1998, 120(2): 337–342.DOI:10.1115/1.2841411 |
| [5] | BONS J P. A review of surface roughness effects in gas turbines[J].Journal of Turbomachinery, 2010, 132(2): 021004.DOI:10.1115/1.3066315 |
| [6] | TAYLOR R P. Surface roughness measurements on gas turbine blades[J].Journal of Turbomachinery, 1990, 112(2): 175–180.DOI:10.1115/1.2927630 |
| [7] | BONS J P, TAYLOR R P, MCCLAIN S T, et al. The many faces of turbine surface roughness[J].Journal of Turbomachinery, 2001, 123(4): 739–748.DOI:10.1115/1.1400115 |
| [8] | BARLOW D N, KIM Y W, FLORSCHUETZ LW. Transient liquid crystal technique for convective heat transfer on rough surfaces[J].Journal of Turbomachinery, 1997, 119(1): 14–22.DOI:10.1115/1.2841004 |
| [9] | HOSNI M H, COLEMAN H W, TAYLOR R P. Rough-wall heat transfer in turbulent boundary layers[J].International Journal of Fluid Mechanics, 1998, 25(1-3): 212–219.DOI:10.1615/InterJFluidMechRes.v25.i1-3 |
| [10] | ABUAF N N, BUNKER R S, LEE C P. Effects of surface roughness on heat transfer and aerodynamic performance of turbine airfoils[J].Journal of Turbomachinery, 1998, 120(3): 522–529.DOI:10.1115/1.2841749 |
| [11] | BUNKER R S.Separate and combined effects of surface roughness and turbulence intensity on vane heat transfer:97-GT-135[R].New York:ASME, 1997. |
| [12] | BOYLE R J, SPUCKLER C M, LUCCI B L, et al. Infrared low-temperature turbine vane rough surface heat transfer measurements[J].Journal of Turbomachinery, 2001, 123(1): 168–177.DOI:10.1115/1.1333693 |
| [13] | BLAIR M F. An experimental study of heat transfer in a large-scale turbine rotor passage[J].Journal of Turbomachinery, 1994, 116(1): 1–13.DOI:10.1115/1.2928273 |
| [14] | STRIPF M, SCHULZ A, BAUER H J, et al. Extended models for transitional rough wall boundary layers with heat transfer-Part Ⅰ:Model formulations[J].Journal of Turbomachinery, 2009, 131(3): 1263–1275. |
| [15] | STRIPF M, SCHULZ A, BAUER H J, et al. Extended models for transitional rough wall boundary layers with heat transfer-Part Ⅱ:Model validation and benchmarking[J].Proceedings of the ASME Turbo Expo, 2008, 131(3): 1277–1289. |
| [16] | TAYLOR R P, COLEMAN H W, HODGE B K.A discrete element prediction approach for turbulent flow over rough surfaces[C]//Viscous and Interacting Flow Field Effects.1984, 1:1-11. |
| [17] | TAYLOR R P, COLEMAN H W, HODGE B K. Prediction of turbulent rough-wall skin friction using a discrete element approach[J].Journal of Fluids Engineering, 1985, 107(2): 251–257.DOI:10.1115/1.3242469 |
| [18] | BOYLE R J, STRIPF M. Simplified approach to predicting rough surface transition[J].Journal of Turbomachinery, 2009, 131(4): 10–20. |
| [19] | LORENZ M, SCHULZ A, BAUER H J. Predicting rough wall heat transfer and skin friction in transitional boundary layers-A new correlation for bypass transition onset[J].Journal of Turbomachinery, 2013, 135(4): 10–21. |
| [20] | HELLSTEN A, SEPPO L.Extension of the k-ω SST turbulence model for flows over rough surfaces:AIAA-1997-3577[R].Reston:AIAA, 1997. |
| [21] | AUPOIX B B. Roughness corrections for the k-ω shear stress transport model:Status and proposals[J].ASME, Journal of Fluids Engineering, 2014, 137(2): 021202.DOI:10.1115/1.4028122 |
| [22] | BELLUCCI J, RUBECHINI F, MARCOCINI M, et al. The influence of roughness on a high-pressure steam turbine stage:An experimental and numerical study[J].Journal of Engineering for Gas Turbines & Power, 2015, 137(1): 012602. |
| [23] | LANGTRY R B, MENTER F R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes[J].AIAA Journal, 2009, 47(12): 2894–2906.DOI:10.2514/1.42362 |
| [24] | MENTER F R, LANGTRY R B, V?LKER S. Transition modelling for general purpose CFD codes[J].Flow, Turbulence and Combustion, 2006, 77(1-4): 277–303.DOI:10.1007/s10494-006-9047-1 |
| [25] | STRIPF M, SCHULZ A, BAUER H J. Modeling of rough wall boundary layer transition and heat transfer on turbine airfoils[J].Proceedings of the ASME Turbo Expo, 2006, 130(2): 1139–1151. |
| [26] | 陈懋章. 粘性流体动力学基础[M].北京: 高等教育出版社, 2002: 312-314.CHEN M Z. Fundamentals of viscous fluid dynamics[M].Beijing: Higher Education Press, 2002: 312-314.(in Chinese) |
| [27] | 郑赟. 基于非结构网格的气动弹性数值方法研究[J].航空动力学报, 2009, 24(9): 2069–2077.ZHENG Y. Computational aero-elasticity with an unstructured grid method[J].Journal of Aerospace Power, 2009, 24(9): 2069–2077.(in Chinese) |
| [28] | 肖大启, 郑赟, 杨慧. 轴向间距对转子叶片气动激励的影响[J].航空动力学报, 2012, 27(10): 2307–2313.XIAO D Q, ZHENG Y, YANG H. Effect of axial spacing on aerodynamic excitation of rotor blade[J].Journal of Aerospace Power, 2012, 27(10): 2307–2313.(in Chinese) |
| [29] | 郑赟, 李虹杨, 刘大响. γ-Reθ转捩模型在高超声速下的应用及分析[J].推进技术, 2014, 35(3): 296–304.ZHENG Y, LI H Y, LIU D X. Application and analysis of γ-Reθ transition model in hypersonic flow[J].Journal of Propulsion Technology, 2014, 35(3): 296–304.(in Chinese) |
| [30] | 郑赟, 李虹杨. 基于新的经验关联公式的γ-Reθ转捩模型在高超声速流动中的应用[J].推进技术, 2015, 36(6): 839–845.ZHENG Y, LI H Y. Application of γ-Reθ transition model in hypersonic flow based on new correlation equation[J].Journal of Propulsion Technology, 2015, 36(6): 839–845.(in Chinese) |
| [31] | WANG T, MATTHEW C R. Effect of elevated free-stream turbulence on transitional flow heat transfer over dual-scaled rough surfaces[J].Journal of Heat Transfer, 2005, 127(4): 393–403.DOI:10.1115/1.1861920 |
| [32] | PINSON M W, WANG T. Effect of two-scale roughness on boundary layer transition over a heated flat plate:Part 2-Boundary layer structure[J].Journal of Turbomachinery, 2000, 122(2): 308–316.DOI:10.1115/1.555454 |
| [33] | STRIPF M. Surface roughness effects on external heat transfer of a HP turbine vane[J].Journal of Turbomachinery, 2005, 127(1): 200–208.DOI:10.1115/1.1811101 |
| [34] | HYLTON L D, MIHELC M S, TURNER E R, et al.Analytical and experimental evaluation of the heat transfer distribution over the surfaces of turbine vanes[C]//AAS/Division of Dynamical Astronomy Meeting.1983. |
