在单模态RT不稳定性的发展初期,由于扰动振幅较扰动波长λ是一个小量,其动力学特性可以用数学上处理比较简单的线性理论来描述。在线性理论中,扰动振幅将随时间以指数的形式增长。在忽略表面张力和流体黏性的条件下,线性增长率可表示为
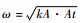
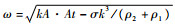
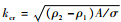
当初始扰动的振幅由于RT不稳定性指数增长到可以与波长相比较时,由于此时的非线性影响不再可以忽略,扰动的发展将偏离线性理论。实验中可以观察到在RT不稳定性的非线性发展阶段,界面将呈现不对称的气泡(bubble)和尖钉(spike)形状,而且气泡以恒定的速度向高密度的液层推进发展。Goncharov[14]基于渐进势流模型从理论上推出了二维和三维情况下此恒定速度的表达式。
由于非线性在数学处理上的复杂性,虽然可以推导出局部个别参数(如气泡的恒定推进速度)的渐进解,但是很难得到描述全局范围动力学特性的解析解(如流体内的压力场和速度场分布)。近年来,随着计算机计算速度以及计算方法的不断发展,利用数值模拟研究RT不稳定性的研究也越来越多。Baker等[15]利用涡层方法(vortex sheet method)模拟了无黏、不可压流体的二维RT不稳定性发展过程,并研究了液层厚度的影响规律。Ramaprabhu等[16-17]通过模拟三维RT不稳定性研究了不同Atwood数下(0.005~1)界面的发展特性。在国内,叶文华等[18-20]利用高精度的通量校正传输(Flux Corrected Transport,FCT)方法对激光烧蚀RT不稳定性进行了模拟,研究了电子热传导烧蚀在长波长扰动的非线性RT不稳定性演变中所起的作用。程会方等[21]利用移动粒子半隐式法(Moving-Particle Semi-implicit method,MPS)模拟了二维RT不稳定性,得到的界面形状与实验结果在表观上基本一致。
可以看出,以往关于RT不稳定性非线性动力学特性的研究主要集中于气泡,尤其是气泡的恒定推进速度上。但是,在利用RT不稳定性实现液体雾化的应用方面,尖钉的动力学特性更加重要。恒定的气泡推进速度意味着恒定的液体波谷表面下沉速度,进而使液体以恒定的速度流入尖钉区域,使尖钉顶部以恒定的速度破碎形成小液滴。因此,深入研究这些恒定的非线性动力学特性将有利于更好地利用RT不稳定性实现雾化。本文基于数值计算得到的压力场与速度场结果,对RT不稳定性的非线性动力学特性,尤其是对液体雾化起重要作用的恒定特性进行了深入分析。
1 物理模型和计算方法 1.1 控制方程 本文考虑气-液两相流的RT不稳定性。密度为ρ1的气体层覆盖在密度为ρ2(ρ2>ρ1)的液体层上方,且整个系统以恒定的加速度A+g向下加速运动,g为重力加速度。本文中气体和液体均被视为理想不可压的牛顿流体。液体雾化过程中液-气密度之比较大,一般在100~1 000范围内变化,因而典型的Atwood数At非常接近于1。为保证数值计算的稳定性,本文选取的液-气密度比ρ2/ρ1为100,相应的Atwood数At为0.98。将参考坐标系固定在底面固壁上,则作用于流体系统的有效惯性加速度为A,如图 1所示。图中:ξ为表面变形的位移。在此参考坐标系下,整个系统的控制方程为
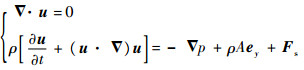 | (1) |
式中:u为速度矢量;ρ为流体密度函数;p为流体压强;ey为y方向上的单位向量。
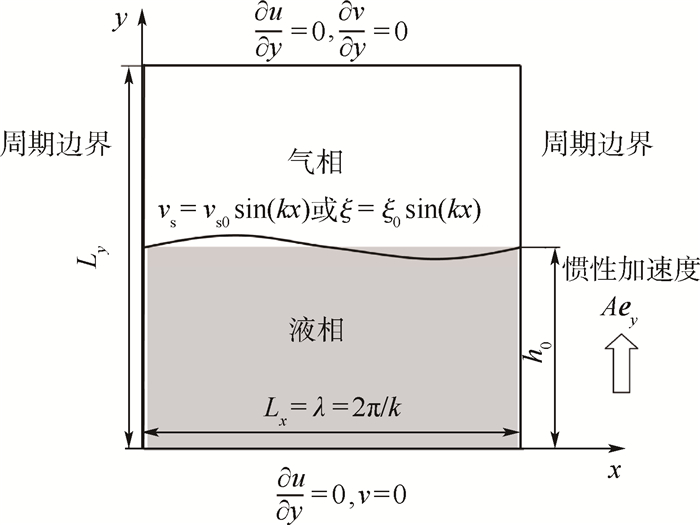 |
| 图 1 物理模型示意图 Fig. 1 Schematic of physical model |
| 图选项 |
表面张力通过连续表面力(Continuum Surface Force, CSF)模型[22]转化为体积力Fs进入控制方程。
本文分别选取lch=λ,
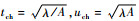
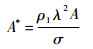 | (2) |
式中:A*表征了起不稳定作用的惯性力和起稳定作用的表面张力之间的比值。
1.2 定解条件 本文计算在二维矩形区域内进行,计算区域的尺寸如图 1所示。在水平方向(x方向),由于只考虑单模态扰动的RT不稳定性,选取x方向的跨度为Lx=λ=2π/k。根据文献[15],形成尖钉的流体动力学行为均发生在距离表面1/k的范围之内,因此,本文选取液层的初始厚度h0=λ>1/k。虽然随着时间的发展,液层的波谷表面会下降,但在本文所有的模拟工况中,在计算结束时液层表面的最低点到底面固壁的距离仍有0.5λ>1/k。所以,液层厚度在本文中不会对尖钉的动力学特性产生较大的影响。为给尖钉提供足够的纵向发展空间,气层竖直方向的跨度设为1.5λ,整个计算区域竖直方向的总跨度为Ly=2.5λ。
在计算开始时,给予气-液界面一个非常小的正弦竖直速度初始扰动vs(t=0, x)=vs0sin(kx)。计算区域的左边界和右边界均设为周期边界,底部边界设为滑移壁面,顶部边界设为自由边界。具体的初始和边界条件已标示在图 1中。
本文采用均匀交错网格对计算区域进行离散化。为确定网格的尺寸,笔者研究了典型模拟工况下(A*=8.8π3)不同网格(Δ=Δx=Δy=λ/16,λ/32,λ/40,λ/48,λ/56,λ/64)对主要非线性动力学参数(恒定波谷沉降速度V和波谷振幅δ0)的影响,如图 2所示。结果显示,当小于λ/48之后,网格尺寸对主要的非线性动力学特性影响非常小。本文数值模拟采用的网格尺寸为Δ=Δx=Δy=λ/64。时间步长Δt受2个条件的限制,即自由表面和表面张力波在一个时间步长内不能移动超过一个网格尺寸的距离。
 | (3) |
式中:Cr为Courant数,本文中取为0.25;umax和vmax分别为每个计算时刻水平速度和竖直速度的最大值。
 |
| 图 2 网格尺寸对波谷沉降速度V和振幅δ0的影响 Fig. 2 Effects of grid sizes on trough descending velocity V and amplitude δ0 |
| 图选项 |
1.3 计算方法 气-液RT不稳定性模拟的关键是气-液界面的捕捉方法。本文采用的计算方法建立在耦合Level-Set和Volume-of-Fluid(CLSVOF)界面捕捉方法基础之上[23]。气-液界面通过一条等LS函数线φ=0隐式表征,而VOF方法作为LS方法的补充以保证液体质量守恒[24]。数值计算方法的细节可参考文献[25],作者利用同样的数值计算方法成功研究了Faraday不稳定性中具体的动力学特性。
1.4 数值验证 为验证本文所用数值方法以及程序代码的正确性,将利用本文代码的计算结果与Baker等[26]利用涡层方法进行模拟的结果进行比较。图 3给出了初始扰动振幅为0.1λ条件下,尖钉顶点和气泡顶点位移随时间的变化规律。图中还给出了线性理论解作为参考。可以看出,无论在线性发展阶段还是非线性发展阶段,利用本文程序代码计算的结果与Baker等[26]的计算结果符合得很好。
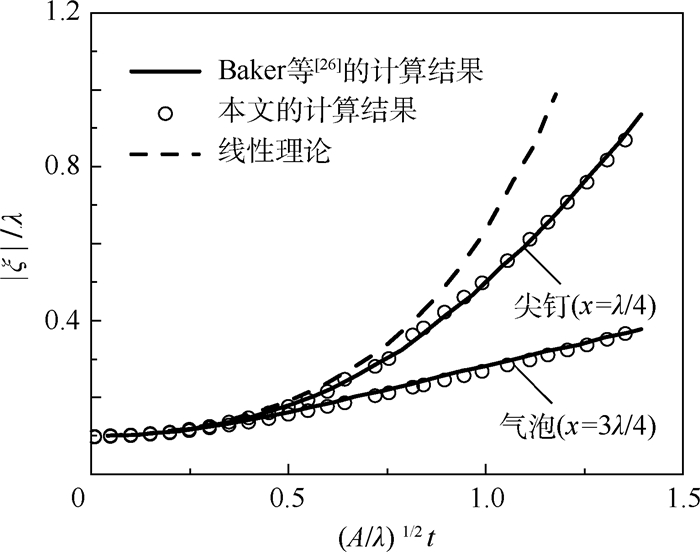 |
| 图 3 模型验证结果 Fig. 3 Results of model validation |
| 图选项 |
2 计算结果与讨论 从RT不稳定性线性增长率的表达式可以看到,对于大Atwood数,只有在无量纲参数A*=ρ1λ2A/σ>4π2的条件下,表面变形的振幅才能够增长。本文对A*=2.4π3,3.2π3,4.0π3,4.8π3,5.6π3,6.4π3,7.2π3,8.0π3和8.8π3等9个值进行了模拟。所有模拟的初始速度扰动振幅为vs0*=0.001。计算在液体尖钉的顶部到达计算域的上边界后停止。
2.1 非线性表面变形的整体动力学特性 图 4给出了RT不稳定性非线性阶段从液层表面形成尖钉的发展过程。图中所有不同时刻界面形状曲线都是在一个工况下计算得到的。可以看出,在表面波峰的根部会形成一个局部最大压强点pmax,而在这个最大压强点以上则会形成一个动力学上独立于底部液层的尖钉区域。这种动力学特性与Faraday不稳定性非常类似[25]。由于本文关注的是Atwood数很大的情况,因此不会在尖钉顶部出现Kelvin Helmhotz(KH)不稳定性所引起的卷曲(roll-up)结构[16, 26]。
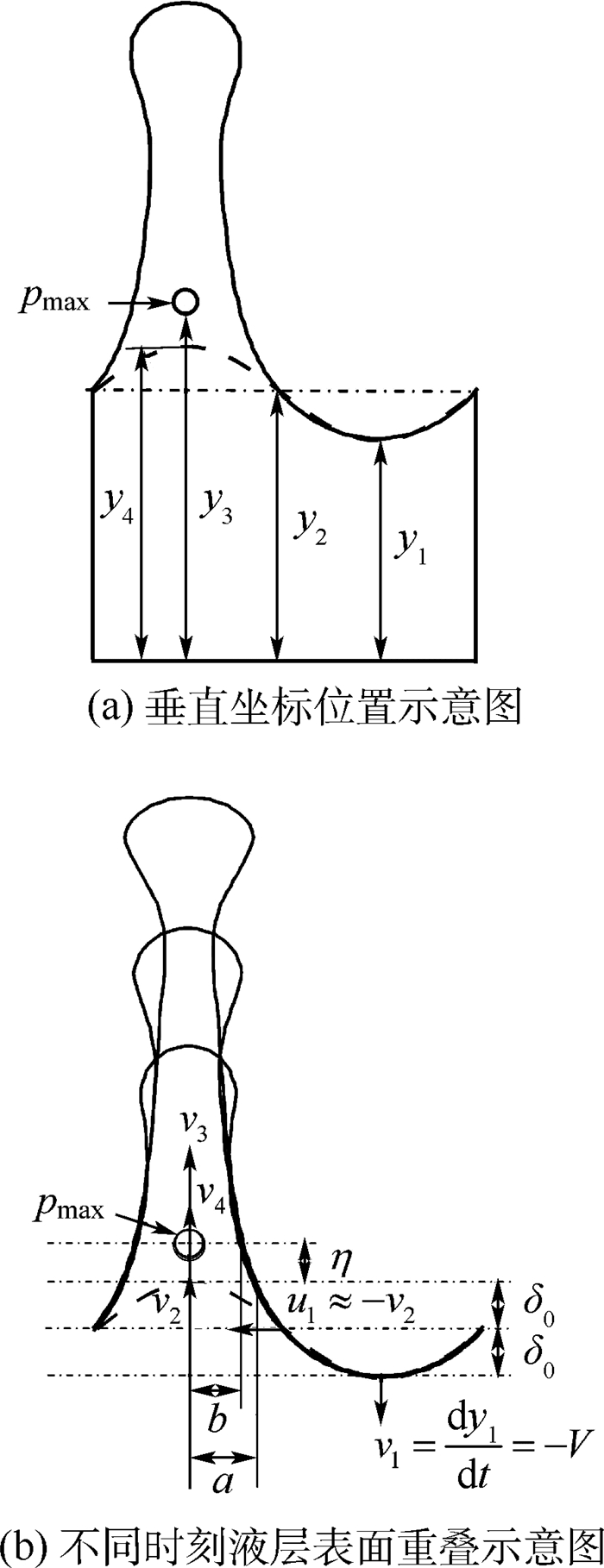 |
| 图 4 液层表面的动力学特征参数 Fig. 4 Features of jet formation from a liquid layer |
| 图选项 |
当把形成局部最大压力点之后不同时刻表面波谷的最低点重叠在一起时,如图 4(b)所示,可以看到如下现象:①不同时刻波谷区域的液面保持着振幅为δ0的正弦曲线形状(如图 4(b)中虚正弦曲线所示);②在波峰区域可以看到不同时刻的最大压力点(如图 4(b)中的小圆圈所示)重合在一起,而且最大压力点到虚正弦波峰顶点的距离η也保持恒定的值。
图 5给出了模拟工况A*=4.8π3下,波谷最低点的垂直坐标y1*(常被称为气泡顶点)、表面变形中性点的垂直坐标y2*和局部最大压力点的垂直坐标y3*随时间的变化规律曲线。作为参考,图 5也给出了线性理论中y1*、表面变形中性点与波谷最低点的距离y2*-y1*以及最大压力点与虚正弦波峰顶点的距离y3*-y4*随时间的变化曲线。其他模拟工况下的各曲线变化规律与图 5相似。
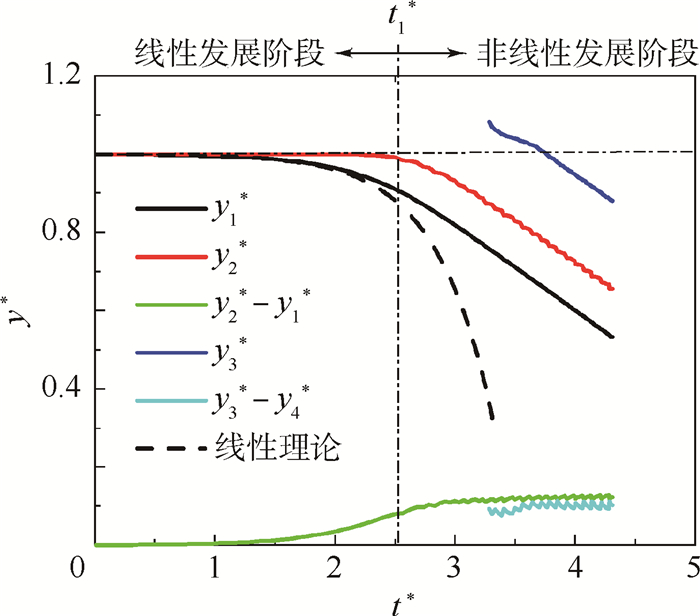 |
| 图 5 y1*、y2*、y3*、y2*-y1*和y3*-y4*随时间的变化曲线 Fig. 5 Temporal changing curves of y1*, y2*, y3*, y2*-y1* and y3*-y4* |
| 图选项 |
从图 5中可以看出,在发展的初始阶段,表面变形严格地遵循线性理论解:
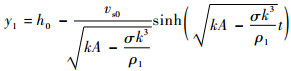 | (4) |
随着表面振幅的不断增大,非线性因素变得逐渐明显,从而降低了表面振幅的增长速度,最终,波谷以恒定的速度V*向下沉降。在线性理论中,中性表面的高度y2*会保持在平衡位置,即h0*=1,然而由于非线性的影响,y2*在某个时刻t*=t1*之后开始以与波谷沉降相同的速度下降,因而使波谷正弦表面的振幅保持在一个固定值δ0*上。可以t*=t1*为界将整个发展过程分为2个阶段:线性发展阶段(t* < t1*)和非线性发展阶段(t*>t1*)。从图 5中还可以看出,y3*、y1*和y2*的下降速度一致,这表明最大压力点与波谷表面作为一个整体以恒定的速度向下沉降。值得注意的是,直到计算结束,液体表面最低点到底面固壁的距离仍然保持在y1*=y1/λ≈0.5以上,因此,图 5中所示的所有稳态动力学特性与底面的固壁边界条件无关。
从图 5中可以看出,y2*-y1*和y3*-y4*最终分别达到恒定值δ0*和η*。
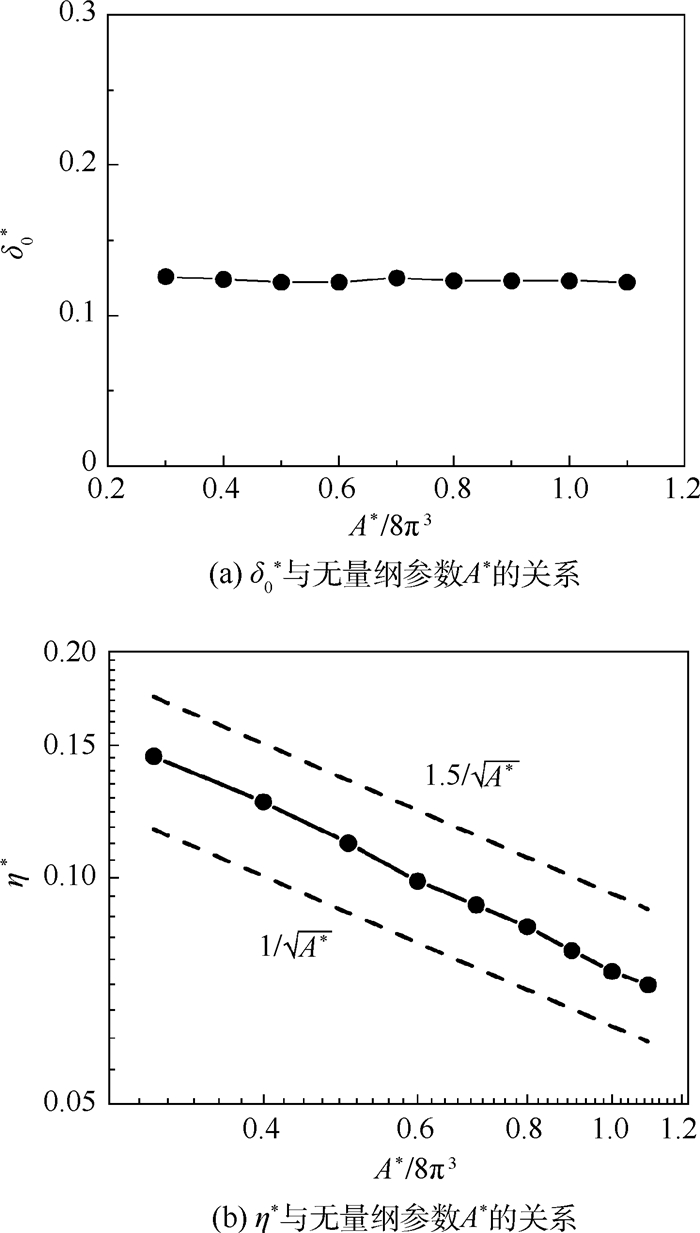
图 6给出了δ0*和η*与无量纲参数A*的关系。δ0*与A*的取值无关,始终保持在0.125左右,而η*则会随着A*的增加而减小,通过数据拟合,可以得到如下关系:
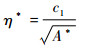 | (5) |
式中:c1=1.26。
 |
| 图 6 δ0*、η*与无量纲参数A*的关 Fig. 6 Dependence of δ0* and η* on dimensionless parameter A* |
| 图选项 |
2.2 稳态流动的动力学特性
2.2.1 波谷表面的恒定沉降速度V* 从图 4(b)和图 5可以看出,在非线性发展阶段,整个波谷表面都以相同的速度V*向下沉降。这个速度就是RT不稳定性研究中提及的气泡推进速度。图 7给出了模拟工况A*=3.2π3,4.8π3,6.4π3和8.0π3下波谷最低点的无量纲竖直方向速度v1*随时间的变化规律。可以看到所有模拟工况下,v1*的值最终都会稳定在一个常数,即
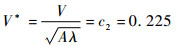 | (6) |
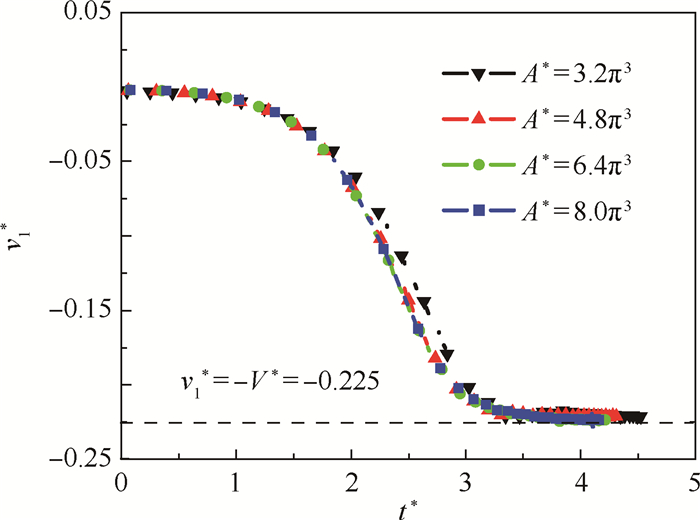 |
| 图 7 不同工况下v1*随时间的变化规律 Fig. 7 Temporal changes of v1* under different cases |
| 图选项 |
Baker等[26]利用涡层方法得到了与式(6)相同的数值。渐进势流模型理论[14]给出At=1的条件下二维气泡顶点推进速度为
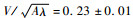
沿着波谷中心线(x*=0.75),由于对称性,水平方向的速度u*=0,因此y方向上液体区域的无量纲动量方程可表示为
 | (7) |
图 8(a)给出了模拟工况A*=4.8π3下非线性发展阶段不同时刻t*=3.41,3.66,3.90,4.14沿波谷中心线的无量纲压强分布规律。可以看到,随着波谷表面的沉降,无量纲压强相应地增大。当把图 8(a)中的纵坐标y*替换为ζ*=y*-y1*之后(见图 8(b)),可以看到所有的压力曲线几乎重合在一起,表明随时间变化的压力函数p*(x*, y*, t*)在非线性发展阶段可以写为2个变量的函数p*(x*, ζ*)。另外,从图 4和图 5已经知道,在非线性发展阶段,整个正弦表面(包括正弦波谷和虚正弦波峰)以及最大压力点都以相同的稳定速度沉降。当站在波谷表面最低点来观察时,最大压力点以下的液体流动为稳态流动,因此竖直方向速度可以表示为v*(x*, y*, t*)=v*(x*, ζ*),则式(7)可以化简为
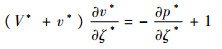 | (8) |
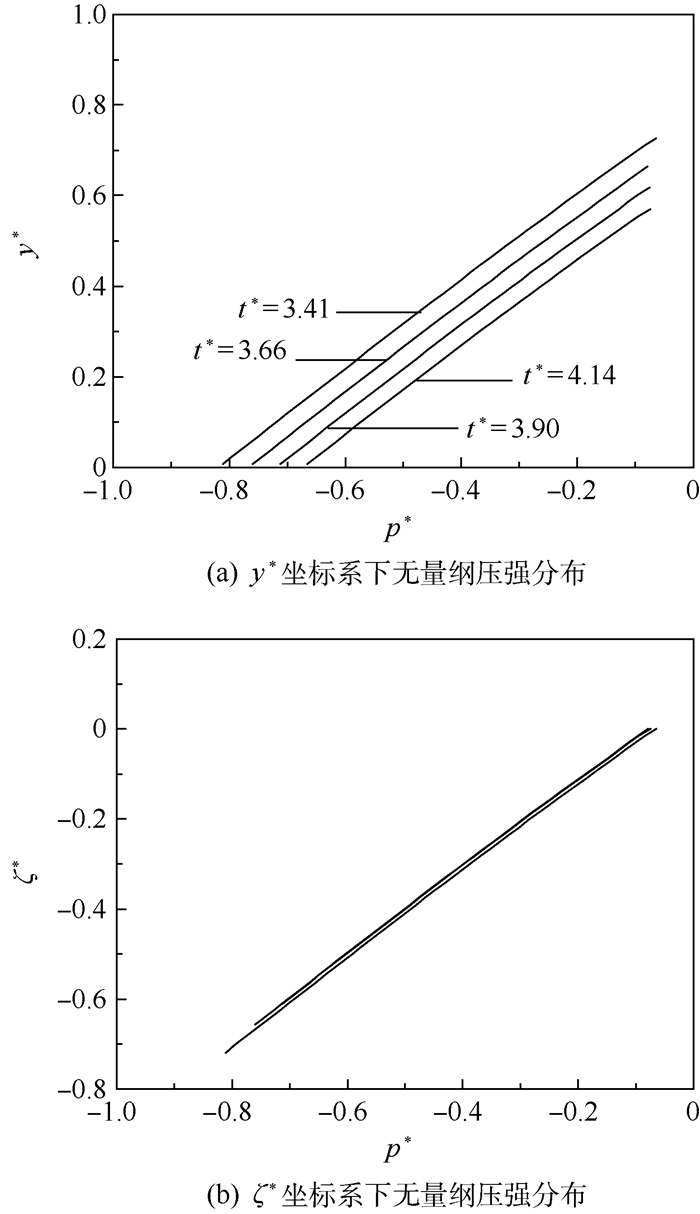 |
| 图 8 不同时刻波谷中心线无量纲压强的分布规律 Fig. 8 Dimensionless pressure distribution of trough center line at different time |
| 图选项 |
将式(8)沿波谷中心线对变量ζ*从ζ0*=-y1*(对应y*=0)到ζ1*=0(对应y*=y1*)进行积分,得
 | (9) |
忽略波谷最低点处的表面张力压强,即p*(x*=0.75, ζ1*)=0,可以得到
 | (10) |
图 9给出了模拟工况A*=4.8π3下非线性发展阶段不同时刻t*=3.41,3.66,3.90,4.14沿波峰中心线(x*=0.25)的无量纲压强分布规律。可以看到,除了尖钉顶端区域由于顶部收缩引起的较大表面压强外,在最大压力点(实心黑点)以上液体尖钉区域内的压力会缓和到与周围气体压力相一致。而由于本文中的Atwood数接近于1,液-气密度比较大,因此在这个液体尖钉区域内的压强p*及其竖直方向梯度?p*/?y*(=?p*/?ζ*)都接近于0。比较图 9(a)与图 8(a)可以看到,在接近底部壁面区域,沿波峰中心线的压强分布与沿波谷中心线的压强分布一致,即
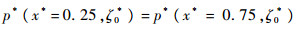 | (11) |
 |
| 图 9 不同时刻波峰中心线处无量纲压强的分布规律 Fig. 9 Dimensionless pressure distribution of crest center line at different time |
| 图选项 |
式(7)和式(8)在波峰中心线上最大压力点以下区域仍然成立。将式(8)沿波峰中心线对变量ζ*从ζ0*=-y1*(对应y*=0)到ζ4*=y4*-y1*(对应y*=y4*)进行积分,得
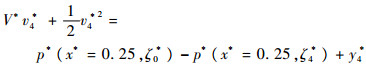 | (12) |
从图 9(b)还可以看到,在虚正弦表面波峰顶点位置y4*处(实心三角形所示)的压强接近于0,即
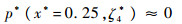 | (13) |
另外,当考虑到非线性发展阶段虚正弦波峰表面与正弦波谷表面以一个整体向下运动,由于质量守恒,则在虚正弦波峰顶点处的竖直方向速度v4*应满足条件:
 | (14) |
计算结果(见图 10)也证实了这个条件。
 |
| 图 10 不同工况下v4*随时间的变化规律 Fig. 10 Temporal changes of v4* under different cases |
| 图选项 |
将式(10)、式(12)~式(14)代入式(11),得
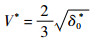 | (15) |
数值结果(见图 6)显示δ0*和无量纲参数A*无关,而且保持在恒定值0.125。笔者将在第2.2.2节中对如何推导得到δ0*进行讨论。从式(15)得到的表面恒定沉降速度V*=0.236,此数值与直接模拟得到的结果(见式(6))以及基于渐进势流模型的理论研究结果[14]吻合得很好。
2.2.2 正弦表面的振幅δ0* 除了波谷表面的恒定沉降速度V*之外,另外一个与稳定流动相关的重要特征量就是数值与无量纲参数A*无关的正弦表面振幅δ0*,其表征了液体尖钉根部、波谷表面附近所形成稳定流的厚度。本节将根据压力场和速度场的计算结果建立模型,推导出δ0*的表达式。
在RT不稳定性中,液体表面的非线性运动学条件为
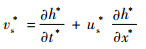 | (16) |
式中:h*(x*, t*)为表面高度函数;us*和vs*分别为表面速度的水平和竖直方向的分量。
在线性理论中,式(16)等号右侧第2项非线性项会被忽略。在线性发展阶段,由于表面各点速度的水平分量us*和表面梯度?h*/?x*都很小,因此这种忽略是合理的。但在非线性发展阶段,由于us*与?h*/?x*的乘积不再是一个小值,因而在分析中必需考虑此项的影响。
图 11给出了模拟工况A*=4.8π3下表面上vs*=0对应点的x坐标随时间的变化规律。可以看到,在整个发展过程中,vs*=0始终是在中性点(x*=0.5, y*=y2*)上。如前所述,在非线性发展阶段,波谷表面可以近似成振幅为δ0*的正弦曲线,因此,波谷区域(x*≥0.5)的表面高度可表示为h*(x*, t*)=y2*(t*)+δ0*sin(2πx*)。在中性点上,式(16)可化简为
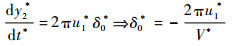 | (17) |
式中:u1*=us*(x*=0.5)为中性点处的水平表面速度。
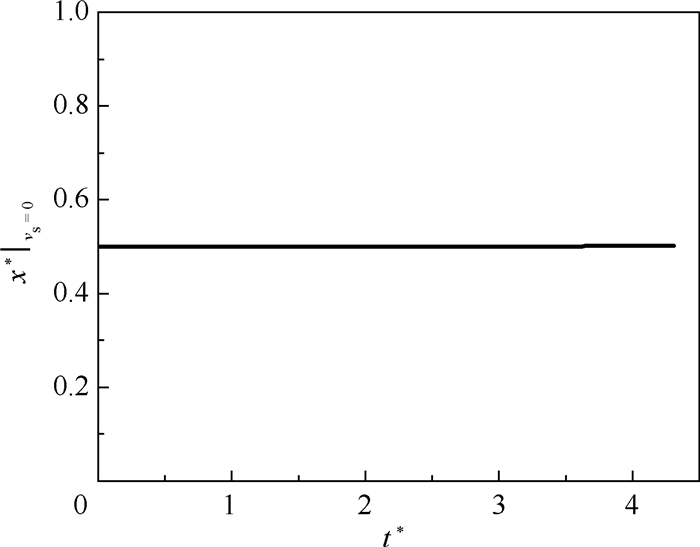 |
| 图 11 表面不动点(vs*=0)所对应的x坐标随时间的变化规 Fig. 11 Temporal changes of x coordinate where vertical velocity vanishes on surface (vs*=0) |
| 图选项 |
在模拟工况A*=4.8π3下,如图 12所示,u1*和位于同一水平面上波峰中心线位置的竖直方向速度v2*=v*(x*=0.25, y*=y2*)大小相同。此关系对其他模拟工况同样成立。
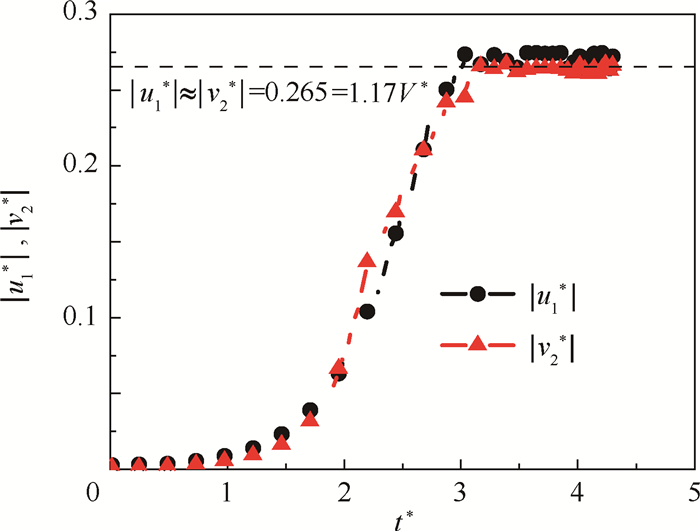 |
| 图 12 |u1*|与|v2*|随时间的变化规律 Fig. 12 Temporal changes of |u1*| and |v2*| |
| 图选项 |
如图 9所示,虚正弦波峰顶部附近(实心三角形)竖直方向的压力梯度|?p*/?ζ*|=|?p*/?y*| < < 1,因此,沿波峰中心线(x*=0.25)在ζ2*=y2*-y1*和ζ4*=y4*-y1*的范围内,式(11)中等号右侧的压力项-?p*/?ζ*可以忽略,即
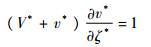 | (18) |
对式(18)从ζ2*到ζ4*积分可得
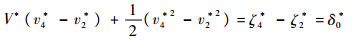 | (19) |
将式(14)和式(15)代入式(19),得
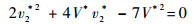 | (20) |
其解为
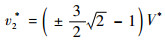 | (21) |
由于v2*应为正,可去除解
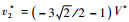
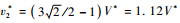
 | (22) |
从式(22)得到的δ0*值较数值计算结果δ0*=0.125略高,这是由于v2*的实际值要比u1*(=1.2V*)略低的结果。
2.2.3 最大压力点处出流速度v3*和出流宽度2b* 从第2.2.1节可以看出,在RT不稳定性中,尖钉底部形成的最大压力点将液体分为2个区域:位于最大压力点以下的稳态流动区和位于最大压力点以上的自由流动区。其中,自由流动区可以看成是在重力作用下液体从喷嘴向下喷出的低速射流问题,而这个最大压力点的位置可以看成是射流问题中喷嘴出口的位置。因此,如果可以确定最大压力点处的出流速度v3*和出流宽度2b*,则射流问题中的研究成果[27-30]就能应用到RT不稳定性诱导雾化领域来。这是以往研究中所忽略的问题。因此,本节将分析如何确定最大压力点处的出流速度v3*和出流宽度2b*。
第2.2.2节中讨论过在虚正弦表面波峰顶点附近的竖直方向压力梯度可以忽略,因此,从式(18)可以得到在虚正弦表面波峰顶点处(x*=0.25, y*=y4*)的速度梯度?v*/?y*(=?v*/?ζ*):
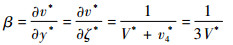 | (23) |
假设竖直方向的速度在y*=y4*到y*=y3*的范围内呈线性分布,且斜率为β,则
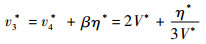 | (24) |
将式(5)代入式(24),得
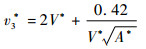 | (25) |
从式(5)和式(25)可以看出,当A*→∞,y3*→y4*且v3*→2V*。因此,当无量纲参数A*足够大时,虚正弦表面波峰顶点和最大压力点重合,出流速度为2V*。
图 13给出了最大压力点处出流半宽b*以及虚正弦表面波峰顶点处出流半宽a*与无量纲参数A*的函数关系。可以看到,a*与A*的取值无关,一直保持为常数c3=0.173,而b*则随着A*的增大而增大。同样,如果A*足够大,y3*→y4*,则
 | (26) |
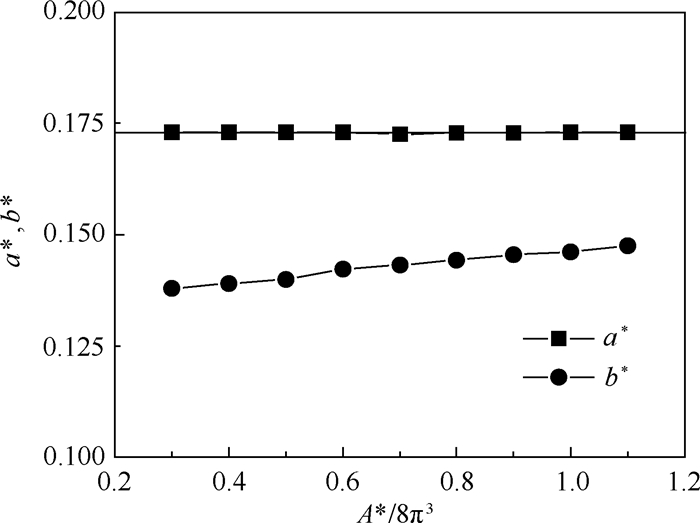 |
| 图 13 a*、b*与无量纲参数A*的关系 Fig. 13 Dependence of a* and b* on dimensionless parameter A* |
| 图选项 |
3 结论 本文利用CLSVOF界面捕捉方法对大Atwood数下二维单模态RT不稳定性进行了数值模拟,重点研究了RT不稳定性尖钉区域非线性发展阶段的稳态动力学特性。通过对计算结果的分析可以得到如下结论:
1)在液体尖钉根部由于惯性力作用而引起的水平冲击流会在此处形成一个局部最大压力点,这个最大压力点将使位于其上部的尖钉区域的发展独立于位于其下部的液层。由于此处惯性力与压强梯度的平衡,位于最大压力点附近的流动最终将达到稳态。
2)在稳态流动中,液体波谷表面可用一条正弦曲线表征,其振幅只与初始扰动的波长有关。波谷表面连同最大压力点将作为一个整体以恒定的速度向下运动,其数值与惯性加速度和波长乘积的平方根成正比。
3)得到了最大压力点处的出流速度和出流宽度与无量纲参数的关系。通过确定这些稳态特征量有助于将经典低速射流的相关理论扩展应用到RT不稳定性诱导雾化的研究领域。
参考文献
| [1] | ARNETT W D, BAHCALL J N, KIRSHNER R P, et al. Supernova 1987A[J].Annual Review of Astronomy and Astrophysics, 1989, 27(2): 629–700. |
| [2] | NORMAN M L, SMARR L, SMITH M D, et al. Hydrodynamic formation of twin-exhaust jets[J].Astrophysical Journal, 1981, 247(1): 52–58. |
| [3] | EVANS R G, BENNETT A J, PERT G J. Rayleigh-Taylor instabilities in laser accelerated targets[J].Physical Review Letters, 1982, 49(22): 1639–1642.DOI:10.1103/PhysRevLett.49.1639 |
| [4] | LINDL J D, MCCRORY R L, CAMPBELL E M. Progress toward ignition and burn propagation in inertial confinement fusion[J].Physics Today, 1992, 45(9): 32–40.DOI:10.1063/1.881318 |
| [5] | BEALE J C. Modeling spray atomization with the Kelvin-Helmholtz/Rayleigh Taylor hybrid model[J].Atomization and Sprays, 1999, 9(6): 623–650.DOI:10.1615/AtomizSpr.v9.i6 |
| [6] | KONG S C, SENECAL P K, REITZ R D. Developments in spray modeling in diesel and direct-injection gasoline engines[J].Oil & Gas Science & Technology, 1999, 54(2): 197–204. |
| [7] | HSIANG L P, FAETH G M. Near-limit drop deformation and secondary breakup[J].International Journal of Multiphase Flow, 1992, 18(5): 635–652.DOI:10.1016/0301-9322(92)90036-G |
| [8] | LEE C H, REITZ R D. An experimental study of the effect of gas density on the distortion and breakup mechanism of drops in high speed gas stream[J].International Journal of Multiphase Flow, 2000, 26(2): 229–244.DOI:10.1016/S0301-9322(99)00020-8 |
| [9] | 解茂昭. 燃油喷雾场结构和雾化机理[J].力学与实践, 1990, 12(4): 9–15.XIE M Z. The structure of fuel spray field and the mechanism of atomization[J].Mechanics in Engineering, 1990, 12(4): 9–15.(in Chinese) |
| [10] | TAYLOR G. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes.I[J].Proceedings of the Royal Society of London Series A, Mathematical and Physical Sciences, 1950, 201(1065): 192–196.DOI:10.1098/rspa.1950.0052 |
| [11] | BELLMAN R, PENNINGTON R H. Effects of surface tension and viscosity on Taylor instability[J].Quarterly of Applied Mathematics, 1953, 12(2): 151–162. |
| [12] | PIRIZ A R, CORTáZAR O D, CELA J J L, et al. The Rayleigh-Taylor instability[J].American Journal of Physics, 2006, 74(12): 1095–1098.DOI:10.1119/1.2358158 |
| [13] | SHARP D H. An overview of Rayleigh-Taylor instability[J].Physica D:Nonlinear Phenomena, 1984, 12(1-3): 3–10.DOI:10.1016/0167-2789(84)90510-4 |
| [14] | GONCHAROV V N. Analytical model of nonlinear, single-mode, classical Rayleigh-Taylor instability at arbitrary Atwood numbers[J].Physical Review Letters, 2002, 88(13): 134502.DOI:10.1103/PhysRevLett.88.134502 |
| [15] | BAKER G R, MCCRORY R L, VERDON C P, et al. Rayleigh-Taylor instability of fluid layers[J].Journal of Fluid Mechanics, 1987, 178: 161–175.DOI:10.1017/S0022112087001162 |
| [16] | RAMAPRABHU P, DIMONTE G, WOODWARD P, et al. The late-time dynamics of the single-mode Rayleigh-Taylor instability[J].Physics of Fluids, 2012, 24(7): 074107.DOI:10.1063/1.4733396 |
| [17] | RAMAPRABHU P, DIMONTE G, YOUNG Y N, et al. Limits of the potential flow approach to the single-mode Rayleigh-Taylor problem[J].Physical Review E, 2006, 74(6): 202–212. |
| [18] | 叶文华. 激光烧蚀RT不稳定性线性增长率和非线性行为的数值研究[J].强激光与粒子束, 1998, 10(4): 567–572.YE W H. Numerical studies of linear growth rates and nonlinear evolution of laser ablative Rayleigh-Taylor instability[J].High Power Laser and Particle Beams, 1998, 10(4): 567–572.(in Chinese) |
| [19] | 叶文华, 张维岩, 陈光南, 等. 激光烧蚀瑞利-泰勒不稳定性数值研究[J].强激光与粒子束, 1999, 11(5): 613–618.YE W H, ZHANG W Y, CHEN G N, et al. Numerical study of laser ablative Rayleigh-Taylor instability[J].High Power Laser and Particle Beams, 1999, 11(5): 613–618.(in Chinese) |
| [20] | 叶文华, 张维岩, 贺贤土. 烧蚀瑞利-泰勒不稳定性线性增长率的预热致稳公式[J].物理学报, 2000, 49(4): 762–767.YE W H, ZHANG W Y, HE X T. Preheating stabilization formula of linear growth rate for ablative Rayleigh-Taylor instability[J].Acta Physica Sinica, 2000, 49(4): 762–767.(in Chinese) |
| [21] | 程会方, 段日强, 姜胜耀. Rayleigh-Taylor不稳定性的MPS数值模拟[J].核动力工程, 2010, 31(s1): 123–126.CHENG H F, DUAN R Q, JIANG S Y. Numerical simulation of Rayleigh-Taylor instability with MPS method[J].Nuclear Power Engineering, 2010, 31(s1): 123–126.(in Chinese) |
| [22] | BRACKBILL J U, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J].Journal of Computational Physics, 1992, 100(2): 335–354.DOI:10.1016/0021-9991(92)90240-Y |
| [23] | SUSSMAN M, PUCKETT E G. A coupled level set and volume-of-fluid method for computing 3D and axisymmetric incompressible two-phase flows[J].Journal of Computational Physics, 2000, 162(2): 301–337.DOI:10.1006/jcph.2000.6537 |
| [24] | VAN DER PIJL S P, SEGAL A, VUIK C, et al. A mass-conserving level-set method for modeling of multi-phase flows[J].International Journal for Numerical Methods in Fluids, 2005, 47(4): 339–361.DOI:10.1002/(ISSN)1097-0363 |
| [25] | LI Y, UMEMURA A. Two-dimensional numerical investigation on the dynamics of ligament formation by Faraday instability[J].International Journal of Multiphase Flow, 2014, 60(2): 64–75. |
| [26] | BAKER G R, MEIRON D I, ORSZAG S A. Vortex simulations of the Rayleigh-Taylor instability[J].Physics of Fluids, 1980, 23(8): 1485–1490.DOI:10.1063/1.863173 |
| [27] | CLANET C, LASHERAS J C. Transition from dripping to jetting[J].Journal of Fluid Mechanics, 1999, 383: 307–326.DOI:10.1017/S0022112098004066 |
| [28] | EGGERS J, VILLERMAUX E. Physics of liquid jets[J].Reports on Progress in Physics, 2008, 71(3): 509–514. |
| [29] | SCHULKES R M S M. The evolution and bifurcation of a pendant drop[J].Journal of Fluid Mechanics, 1994, 278: 83–100.DOI:10.1017/S0022112094003629 |
| [30] | UMEMURA A. Self-destabilizing mechanism of a laminar inviscid liquid jet issuing from a circular nozzle[J].Physical Review E, 2011, 83(4): 046307.DOI:10.1103/PhysRevE.83.046307 |
