随着现代航空技术的不断发展，各种战斗机和飞行器的机动性能不断提高，对于多机动目标跟踪变得尤为重要。但由于噪声、杂波、目标机动、数据关联和检测不确定的存在，使得多机动目标跟踪无论在理论还是实现上都变得非常困难^[1-3]。跳变马尔可夫系统(Jump Markov System，JMS)被证明是目前比较有效的单机动目标跟踪工具^[4-5]，同时与传统的数据关联技术结合实现对多机动目标跟踪，如联合概率数据关联^[6]、多假设跟踪^[7]。但这些基于数据关联的方法，随着目标数或者杂波数的增加，其计算量指数增长，严重制约了其发展和应用。
近年来，Mahler^[8]以有限集统计学为基础，提出了随机有限集(Random Finite Set，RFS)方法，该方法提供了一个简洁的公式描述多目标跟踪，避免了数据关联^[8-9]。随机有限集方法很快成为了多目标跟踪的研究热点之一。许多国内外****研究将RFS与JMS结合，实现对多机动目标的跟踪^[10-14]。但在这些研究中都假设杂波密度是一个时不变的先验已知参数。而实际中杂波密度是未知且可能随着环境的改变而变化，当采用的杂波密度与实际的不相符时会导致严重的滤波偏差，甚至出现完全错误的滤波，因此估计杂波密度是非常困难且重要的。最近，一些国外****提出了基于RFS的未知杂波密度多目标跟踪方法^[15-17]。文献[15]给出了一种结合概率假设密度(PHD)滤波的最大似然方法估计杂波密度。文献[16]推导了一种新的PHD和势概率假设密度(Cardinalized Probability Hypothesis Density，CPHD)滤波形式，可实现在滤波中实时地估计杂波密度。文献[17]给出了一种适用于非线性模型和未知杂波密度的多伯努利滤波算法。而这些研究又都没有考虑目标的机动性，在目标发生机动时性能会严重下降。
针对以上问题，本文提出了一种未知杂波密度的多机动目标跟踪算法，称为线性高斯JMS未知杂波密度GMPHD(LGJMS-λ-GMPHD)滤波算法。该算法以未知杂波密度GMPHD滤波为基础，推导了在LGJMS下未知杂波密度GMPHD迭代的完全解析表达式。仿真结果表明，无论是对于未知固定杂波密度还是未知时变杂波密度的场景，本文算法都可实现对于杂波密度以及目标数和目标状态的准确估计。
1 λ-GMPHD原理 为了解决基于RFS的未知杂波密度多目标跟踪，Mahler等^[16]给出了一种可联合估计杂波密度和目标状态的PHD滤波器，称为λ-PHD滤波器。其核心思想是将杂波建模为与真实目标类似的杂波目标，同样包括预测中目标的新生、衍生、消亡、转移和以确定的检测概率产生杂波量测，但却与真实目标相互独立。假定k-1时刻，真实目标状态为X_k-1⁽¹⁾，杂波目标状态为X_k-1⁽⁰⁾，则该时刻联合多目标状态为。在k时刻，根据多目标运动过程^[8]，联合多目标状态可表示为，其中:

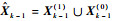
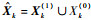
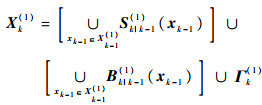(1)

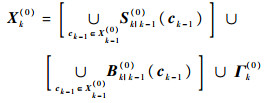(2)

式中：Γ_k⁽ⁱ⁾表示新生目标状态RFS；B_k|k-1⁽ⁱ⁾(x_k-1/c_k-1)表示从x_k-1/c_k-1衍生出目标状态RFS；S_k|k-1⁽ⁱ⁾(x_k-1/c_k-1)表示存活目标状态RFS。联合多目标状态产生的量测Z_k表示为Z_k=D_k⁽¹⁾(X_k⁽¹⁾)∪D_k⁽⁰⁾(X_k⁽⁰⁾)，其中D_k⁽¹⁾(X_k⁽¹⁾)=表示真实目标产生量测；表示杂波目标量测。对于λ-PHD滤波器，迭代传递的后验强度可表示为

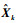
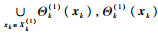
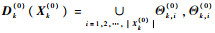
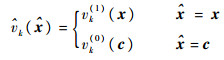(3)

式中：v_k⁽¹⁾(·)和v_k⁽⁰⁾(·)分别为真实目标和杂波目标强度。由于杂波目标的产生过程不依赖其状态c且独立同分布，因此v_k⁽⁰⁾(·)可通过平均杂波目标数N_k⁽⁰⁾来描述。同时由于杂波目标服从二项分布，故检测后的平均杂波密度估计为

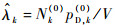式中:p_{D, k}⁽⁰⁾为杂波检测概率; V为量测空间。
为了获得λ-PHD滤波器的完全解析表达式，类似于传统的PHD滤波器做如下假设：
1) 每个真实目标满足线性高斯运动和量测模型，即

式中:N(·; m, Q)为均值为m和方差为Q的高斯密度；F_k-1为状态转移矩阵；Q_k-1为过程协方差矩阵；H_k为量测矩阵；R_k为量测噪声协方差矩阵。
2) 真实目标存在概率和检测概率都状态独立，分别为p_{S, k}⁽¹⁾(x)=p_{S, k}⁽¹⁾，p_{D, k}⁽¹⁾(x)=p_{D, k}⁽¹⁾。
3) 真实目标的衍生目标RFS强度为高斯混合形式

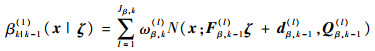4) 新生真实目标RFS强度为高斯混合形式

5) 杂波目标存在概率和检测概率为常数p_{S, k}⁽⁰⁾和p_{D, k}⁽⁰⁾。
6) 杂波目标的平均衍生数为

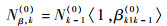7) 杂波目标的平均新生数为

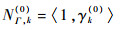则λ-GMPHD滤波器的迭代如下^[16]。
预测????假设已知k-1时刻的真实目标后验强度v_k-1⁽¹⁾和平均杂波目标数N_k-1⁽⁰⁾，且v_k-1⁽¹⁾为高斯混合形式：，则预测真实目标强度v_k|k-1⁽¹⁾为

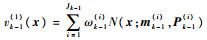
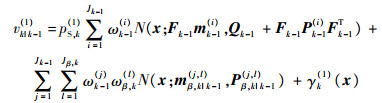(4)

式中:

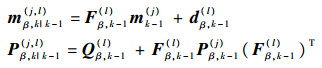预测平均杂波目标数N_k|k-1⁽⁰⁾为

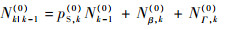(5)

更新????假设已知k时刻的预测真实目标强度v_k|k-1⁽¹⁾和平均杂波目标数N_k|k-1⁽⁰⁾，且v_k|k-1⁽¹⁾为高斯混合形式：，则给定量测Z_k，更新的真实目标后验强度v_k⁽¹⁾为

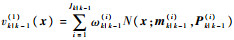
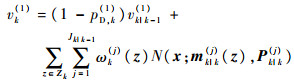(6)

式中：

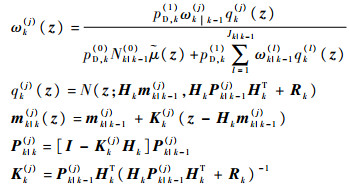更新的平均杂波目标数N_k⁽⁰⁾为

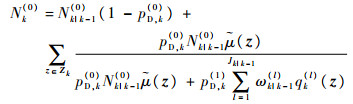(7)

检测后平均杂波密度估计为。
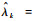
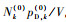
2 LGJMS模型及LGJMS-λ-GMPHD滤波 2.1 LGJMS模型 JMS是目前机动目标跟踪的有效工具。JMS通过一组参数化的状态空间模型来描述，各模型之间服从转移概率为t_k|k-1(r_k|r_k-1)的离散马尔可夫链。JMS将目标状态以马尔可夫形式在不同模型之间转换，找到最佳的匹配模型，完成机动目标跟踪。为了与λ-GMPHD滤波器有效结合，本文考虑线性高斯运动和量测模型的LGJMS，其在模型r_k下的条件状态转移密度和观测似然函数为

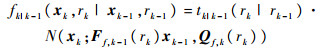(8)

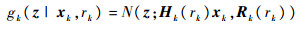(9)

式中：F_{f, k-1}(r_k)和H_k(r_k)为在模型r_k下的转移和量测矩阵；Q_{f, k}(r_k)和R_k(r_k)为相应的过程噪声和量测噪声协方差。新生真实目标强度为

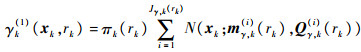(10)

式中：π_k为新生模型分布。衍生真实目标强度为

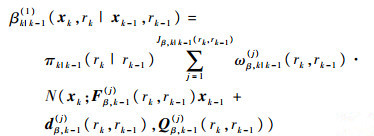(11)

式中：π_k|k-1(r_k|r_k-1)为衍生模型分布。
由于杂波目标的产生过程不依赖其状态，因此不需采用LGJMS来对其进行描述。
2.2 LGJMS-λ-GMPHD滤波 本节在LGJMS基础上，结合λ-GMPHD滤波器，提出了一种解决未知杂波密度的多机动目标跟踪算法，简称为LGJMS-λ-GMPHD滤波算法。该算法依然保持了原始λ-GMPHD滤波算法的数学结构，只是在真实目标的迭代过程中采用了LGJMS模型。其具体推导过程如下。
预测????假设已知k-1时刻的真实目标后验强度v_k-1⁽¹⁾和杂波目标数后验均值N_k-1⁽⁰⁾，且, 则预测真实目标强度v_k|k-1⁽¹⁾为

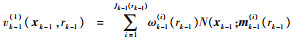
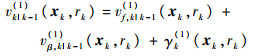(12)

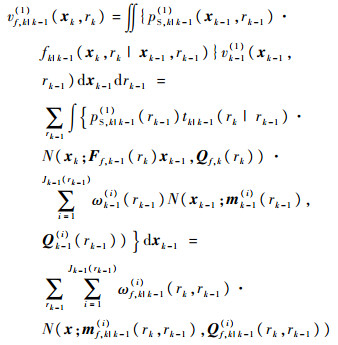(13)

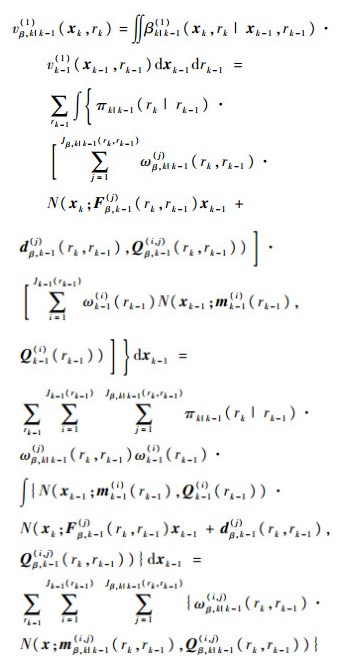(14)

式中:

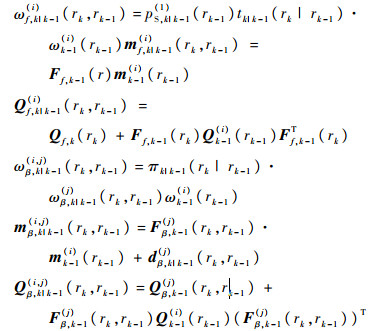预测平均杂波目标数N_k|k-1⁽⁰⁾为

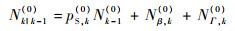(15)

更新????假设已知k时刻的预测真实目标强度v_k|k-1⁽¹⁾和平均杂波目标数N_k|k-1⁽⁰⁾，且v_k|k-1⁽¹⁾为

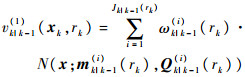则更新的真实目标后验强度v_k⁽¹⁾为

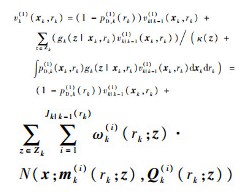(16)

式中:

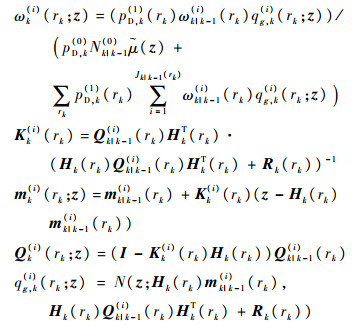真实目标个数N_k⁽¹⁾为

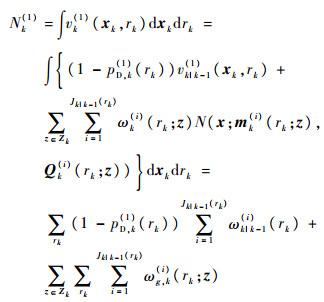(17)

更新的平均杂波目标数N_k⁽⁰⁾为

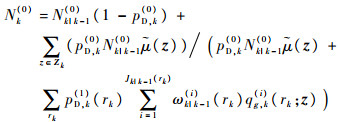(18)

检测后平均杂波密度估计为。
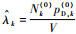
剪枝????由于在预测过程中新生目标及衍生目标的加入和更新过程中高斯项的增加，使得最终表示后验强度的高斯项不断增加。为了降低高斯项，首先删除高斯权重低于门限T的高斯项，其次合并同一模型下距离在U范围内的高斯项。
多目标状态提取????根据估计的真实目标个数，选取对应数目的高斯权重最大的高斯项，其高斯分量的均值作为对应目标状态。
3 仿真分析 3.1 仿真场景设置 采用一个目标数未知且变化的二维多机动目标运动场景来验证本文的算法。量测区域为[-60,60]×[-60,60] km²，传感器位于(0, 0) km处，其采样间隔为5 s，共采样100个时刻。
目标运动状态为，包含目标位置(p_{x, k}, p_{y, k})和速度()。本文采用3种运动模型来描述目标的机动性：模型1服从转弯率为ω₁=0(°)/s、过程噪声标准差为σ₁=5 m·s^-2的直角转弯运动；模型2服从转弯率为ω₂=3(°)/s、过程噪声标准差为σ₂=20 m·s^-2的直角转弯运动；模型3服从转弯率为ω₃=-3(°)/s、过程噪声标准差为σ₃=20 m·s^-2的直角转弯运动。直角转弯运动状态转移和协方差矩阵分别为

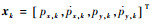
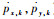
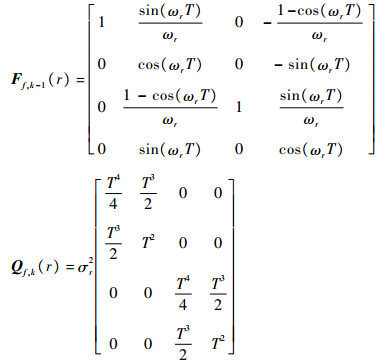运动模型间转换的马尔可夫转移概率矩阵为

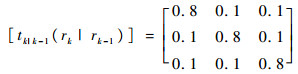为了简单，本文假设对于所有模型r_k-1=1, 2, 3，真实目标存在概率为p_{S, k|k-1}⁽¹⁾(r_k-1)=0.99，检测概率为p_{D, k}⁽¹⁾(r_k)=0.98。新生真实目标强度为，其中目标状态为m_γ⁽¹⁾=[4×10⁴, 0, -5×10⁴, 0]^T，m_γ⁽²⁾=[-5×10⁴, 0, 4×10⁴, 0]^T, m_γ⁽³⁾=[-1×10⁴, 0, 0, 0]^T, P_γ=diag([10⁶, 10⁴, 10⁶, 10⁴]), 模型分布为[π_k(r_k)]=[0.9, 0.05, 0.05]。真实目标的衍生强度为β_k|k-1(x_k, r_k|x_k-1, r_k-1)=0.05π_k|k-1(r_k|r_k-1)N(x_k; x_k-1, Q_{β, k-1})，其中Q_{β, k-1}=diag([10⁴, 5×10², 10⁴, 5×10²])，其模型分布为

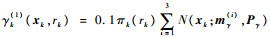
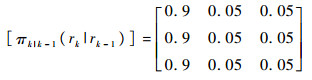平均新生杂波目标数为N_k⁽⁰⁾=10；杂波目标衍生强度为β_k|k-1⁽⁰⁾=0.05。杂波目标存在概率和检测概率分别为p_{S, k}⁽⁰⁾=0.9和p_{D, k}⁽⁰⁾=0.5。杂波量测服从均匀分布。由于平均杂波密度估计和平均杂波率估计存在关系，因此为了仿真中更好地显示对于杂波密度的估计结果，本文采用杂波率来代替杂波密度。对每个高斯项，剪枝门限为T=10^-5，合并距离门限为U=5 m，最大高斯分量数为J_max=100。
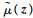
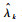
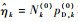
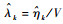
传感器量测模型为z_k=H_k(r_k)x_k+ε_k，其中对于所有模型r_k=1, 2, 3，量测矩阵和量测噪声为和ε_k～N(·; 0, R_k(r_k))，R_k(r_k)=diag([σ_r², σ_r²]^T)，σ_r=40 m。
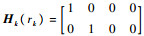
仿真场景中共有5个机动目标，其真实运动轨迹如图 1所示，目标1从第1个采样时刻运动到第91个采样时刻；目标2从第6个采样时刻运动到第96个采样时刻；目标3从第13个采样时刻运动到采样结束；目标4在第32个采样时刻从目标1中衍生出来，运动到结束；目标5在第45个采样时刻从目标2中衍生出来，运动到第81个采样时刻。

图 1 真实目标运动轨迹 Fig. 1 True target trajectories

图选项

3.2 仿真结果
3.2.1 固定杂波密度多机动目标跟踪 首先，采用固定杂波密度的多机动目标运动场景来验证本文的算法。假设以参数为N_k⁽⁰⁾=100，p_{D, k}⁽⁰⁾=0.5的二项分布产生杂波，对应平均杂波密度为3.47×10^-3 km^-2，平均杂波率为50，其他参数与3.1节的设置相同。图 2给出了包含杂波目标的量测。图 3给出了未知杂波密度条件下，LGJMS-λ-GMPHD滤波算法单次仿真实验对多目标位置的估计结果。从仿真结果可看出，给出的算法可在未知杂波密度下正确跟踪单独目标运动和不同的目标新生、衍生和消失。

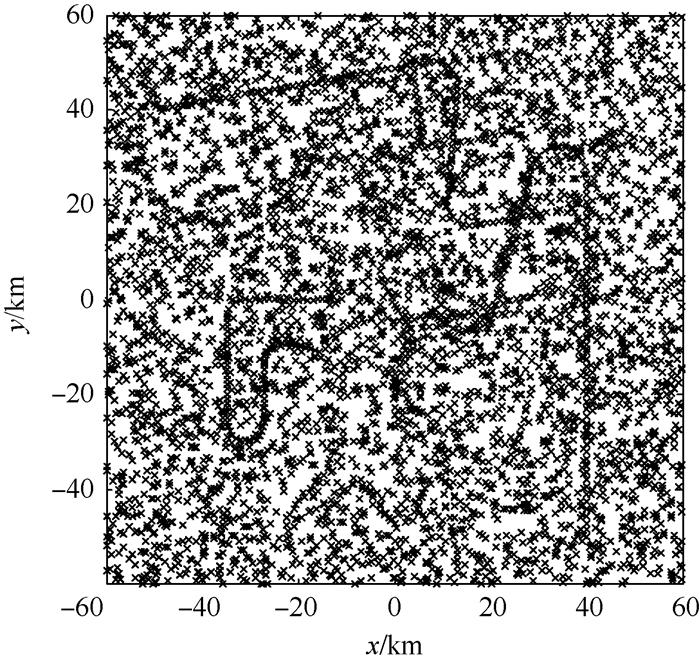图 2 包含杂波目标运动航迹量测结果 Fig. 2 Observation results immersed in clutters of target tracks

图选项

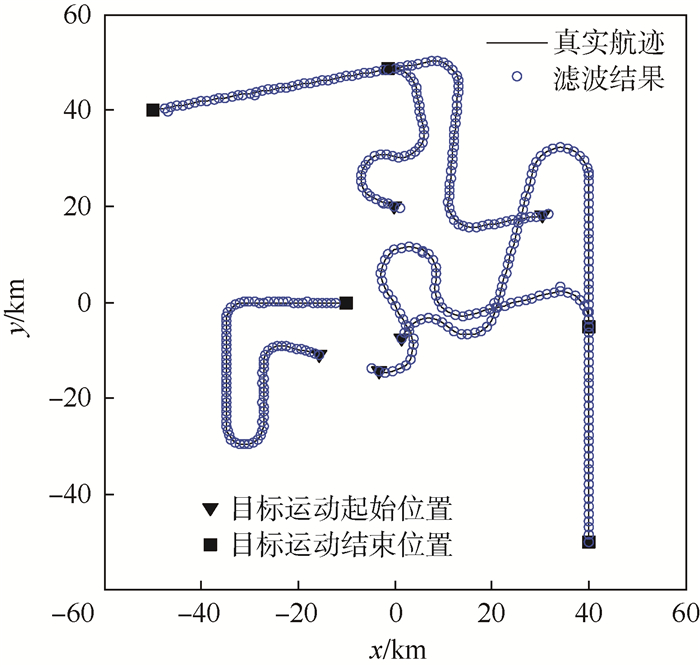图 3 LGJMS-λ-GMPHD滤波算法位置估计 Fig. 3 Position estimations of LGJMS-λ-GMPHD filter algorithm

图选项

图 4给出了100次蒙特卡罗实验，LGJMS-λ-GMPHD滤波算法对于机动目标数和杂波率的统计特性。仿真结果表明，本文算法可以准确地估计目标数和杂波率。

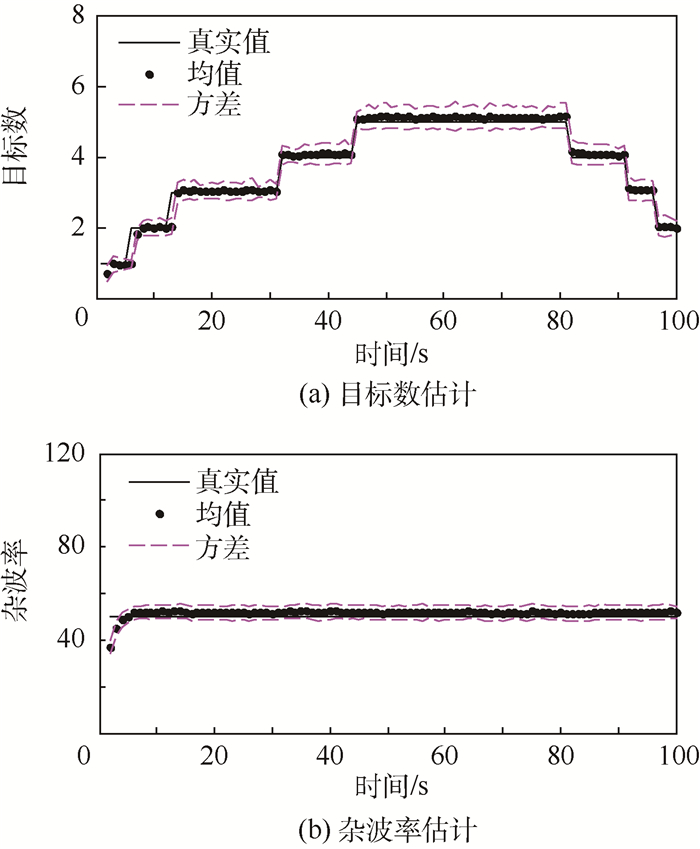图 4 固定杂波密度下目标数和杂波率统计结果 Fig. 4 Statistic results of target number and clutter rate for fixed clutter density

图选项

为了进一步验证本文算法，将其与杂波密度已知的LGJMS-GMPHD滤波算法进行比较。采用最优子模式分配(OSPA)距离^[18]用于定量地分析距离算法的滤波性能。OSPA距离既包含目标位置估计误差，也包含目标个数估计误差，反映了滤波器的综合估计精度，其定义如下^[18]：

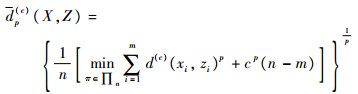(19)

本仿真中取p=2;c=1 000。图 5展示了经100次蒙特卡罗仿真实验平均后得到的二者OSPA距离随时间变化曲线。从图中可以看出，LGJMS-λ-GMPHD滤波算法的OSPA距离接近于杂波密度已知的LGJMS-GMPHD滤波算法，同时发现在采样时刻6和13的时候出现尖峰，这主要是由于该采样时刻对于目标数的估计存在偏差，而OSPA距离在目标数估计错误时会出现峰值。

图 5 固定杂波密度下OSPA距离比较结果 Fig. 5 Comparison results of OSPA metric for fixed clutter density

图选项

3.2.2 时变杂波密度多机动目标跟踪 为了进一步验证对于杂波密度的估计性能，采用时变杂波密度的多机动目标运动场景来验证本文的算法。目标数和杂波率估计的100次蒙特卡罗结果如图 6所示。从图中可以看出，LGJMS-λ-GMPHD滤波算法可以准确地估计目标数，同时对于时变的杂波率也可准确估计。随着杂波密度的增加，目标数和杂波率估计方差都在增大，这主要是由于杂波密度的增大，杂波数增多，降低了算法的性能。

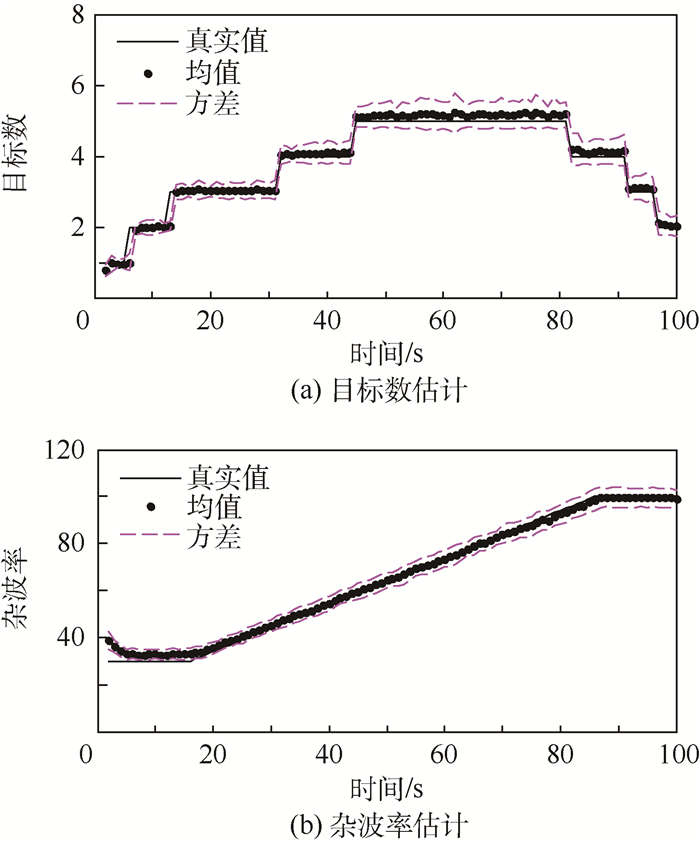图 6 时变杂波密度下目标数和杂波率统计结果 Fig. 6 Statistic results of target number and clutter rate for variable clutter density

图选项

图 7给出了两种算法的OSPA距离。从图中可以看出，LGJMS-λ-GMPHD滤波算法的OSPA距离接近于杂波密度已知的LGJMS-GMPHD滤波算法。同时在采样时刻50之后其OSPA值相比于图 5会变大，这是由于这个时刻之后的杂波密度增大，杂波数增多，滤波性能下降。

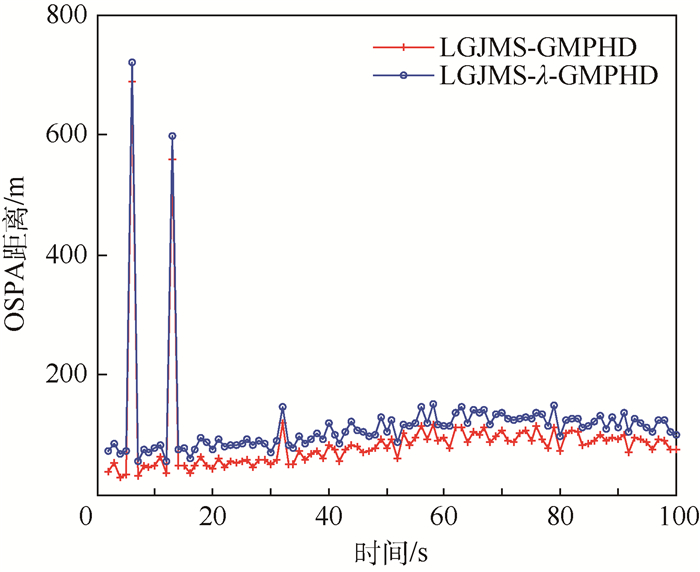图 7 时变杂波密度下OSPA距离比较结果 Fig. 7 Comparison results of OSPA metric for variable clutter density

图选项

3.2.3 不同检测概率多机动目标跟踪 进一步讨论了目标检测概率对于滤波算法的影响。图 8给出了固定杂波密度为3.47×10^-3 km^-2、不同目标检测概率下，100次蒙特卡罗实验的平均OSPA距离值。从图中可以看出，随着目标检测概率的降低，两种算法的OSPA距离都在增大，表明滤波性能都在降低。这主要是由于检测概率的降低，目标丢失率增大，目标数估计误差增大，滤波性能降低。

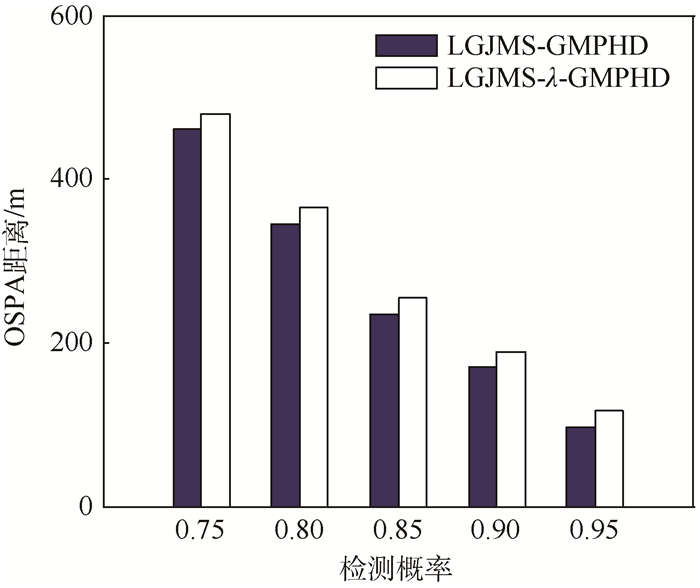图 8 不同检测概率下OSPA距离比较结果 Fig. 8 Comparison results of OSPA metric for different detection probability

图选项

4 结论 基于RFS的多目标跟踪方法已经成为了多目标跟踪领域的研究热点。本文在未知杂波密度GMPHD滤波算法的基础上，结合LGJMS，提出了一种未知杂波密度下多机动目标跟踪算法。仿真实验表明：
1) 本文所提LGJMS-λ-GMPHD滤波算法可实现对于未知固定杂波密度的多机动目标进行准确跟踪和杂波率准确估计，其标准差为3。相比于已知杂波密度的LGJMS-GMPHD滤波算法，其OSPA距离略高，且平均OSPA距离为110.3 m。
2) 本文所提LGJMS-λ-GMPHD滤波算法仍然可实现对于未知且时变杂波密度下多机动目标运动的准确跟踪和杂波率准确估计，随着杂波密度的增加，其杂波率和目标数估计标准差增大，OSPA距离也相应增大。
3) 本文所提LGJMS-λ-GMPHD滤波算法对于随着真实目标检测概率的降低，滤波性能降低，在p_{D, k}⁽¹⁾(r_k)=0.95时，OSPA距离为116.8 m，在p_{D, k}⁽¹⁾(r_k)=0.75时，OSPA距离为480.1 m，其性能下降4倍多。
LGJMS-λ-GMPHD滤波算法由于假设目标运动和量测模型都是线性模型，下一步研究非线性模型下的未知杂波密度多机动目标跟踪方法。

参考文献

[1]	BLACKMAN S S. Multiple-target tracking with radar applications[M].Norwood: Artech House, 1986: 19-44.
[2]	LI X R, JILKOV V P. Survey of maneuvering target tracking.Part I.Dynamic models[J].IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1333–1364.DOI:10.1109/TAES.2003.1261132
[3]	LI X R, JILKOV V P. Survey of maneuvering target tracking.Part V.Multiple-model methods[J].IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1255–1321.DOI:10.1109/TAES.2005.1561886
[4]	BAR-SHALOM Y, LI X R, KIRUBARAJAN T. Estimation with applications to tracking and navigation[M].New York: Wiley, 2001: 421-488.
[5]	BLOM H A P, BAR-SHALOM Y. The interacting multiple model algorithm for systems with Markovian switching coefficients[J].IEEE Transactions on Automatic Control, 1988, 33(8): 780–783.DOI:10.1109/9.1299
[6]	FORTMANN T E, BAR-SHALOM Y, SCHEFFE M. Sonar tracking of multiple targets using joint probabilistic data association[J].IEEE Journal of Oceanic Engineering, 1983, 8(3): 173–184.DOI:10.1109/JOE.1983.1145560
[7]	BLACKMAN S S. Multiple hypothesis tracking for multiple target tracking[J].IEEE Aerospace and Electronic Systems Magazine, 2004, 19(1): 5–18.DOI:10.1109/MAES.2004.1263228
[8]	MAHLER R. Statistical multisource-multitarget information fusion[M].Norwood: Artech House, 2007: 565-682.
[9]	杨威, 付耀文, 龙建乾, 等. 基于有限集统计学理论的多目标跟踪技术研究综述[J].电子学报, 2012, 40(7): 1440–1448.YANG W, FU Y W, LONG J Q, et al. The FISST-based target tracking techniques:A survey[J].Chinese Journal of Electronics, 2012, 40(7): 1440–1448.(in Chinese)
[10]	PUNITHAKUMAR K, KIRUBARAJAN T, SINHA A. Multiple-model probability hypothesis density filter for tracking maneuvering targets[J].IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1): 87–98.DOI:10.1109/TAES.2008.4516991
[11]	PASHA S A, VO B N, TUAN H D, et al. A Gaussian mixture PHD filter for jump Markov system models[J].IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 919–936.DOI:10.1109/TAES.2009.5259174
[12]	FU Y W, LONG J Q, YANG W. Maneuvering multi-target tracking using the multi-model cardinalized probability hypothesis density filter[J].Chinese Journal of Electronics, 2013, 22(3): 634–640.
[13]	DUNNE D, KIRUBARAJAN T. Multiple model multi-Bernoulli filters for manoeuvering targets[J].IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(4): 2679–2692.DOI:10.1109/TAES.2013.6621845
[14]	YANG J L, JI H B, GE H W. Multi-model particle cardinality-balanced multi-target multi-Bernoulli algorithm for multiple manoeuvring target tracking[J].IET Radar, Sonar & Navigation, 2013, 7(2): 101–112.
[15]	CHEN X, THARMARASA R, PELLETIER M, et al. Integrated clutter estimation and target tracking using Poisson point processes[J].IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1210–1235.DOI:10.1109/TAES.2012.6178058
[16]	MAHLER R, VO B T, VO B N. CPHD filtering with unknown clutter rate and detection profile[J].IEEE Transactions on Signal Processing, 2011, 59(8): 3497–3513.DOI:10.1109/TSP.2011.2128316
[17]	VO B T, VO B N, HOSEINNEZHAD R, et al. Robust multi-Bernoulli filtering[J].IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 399–409.DOI:10.1109/JSTSP.2013.2252325
[18]	SCHUHMACHER D, VO B T, VO B N. A consistent metric for performance evaluation of multi-object filters[J].IEEE Transactions on Signal Processing, 2008, 56(8): 3447–3457.DOI:10.1109/TSP.2008.920469