本文通过状态空间传递矩阵(SSM)法建立了梁的理论模型,并采用线性扭转弹簧模拟裂纹对结构局部柔度的贡献,建立了复杂边界条件下功能梯度Timoshenko梁的多损伤模型,并且提出了一种运用差分进化算法对结构损伤进行识别的方法。计算结果表明,本文提出的方法精度较高。
1 理论推导 1.1 基本方程 考虑材料沿轴向指数变化的功能梯度Timoshenko梁,梁的长度为L,梁的截面惯性矩为I,面积为A,材料的弹性模量、剪切模量和密度沿梁的轴向方向服从指数的变化规律[15-16],如图 1所示。为了简化模型,令
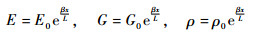 | (1) |
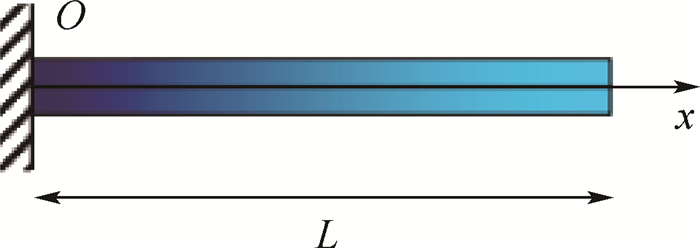 |
| 图 1 材料沿轴向指数分布的功能梯度Timoshenko梁 Fig. 1 Functionally graded Timoshenko beams along axial exponential distribution |
| 图选项 |
式中:β为无量纲的梯度系数;x为沿轴向的坐标; E0、ρ0和G0分别为坐标x=0处的弹性模量、密度和剪切模量。
材料的剪切系数为K,由式(1)可知,当β=0时,梁为均匀材料。由Timoshenko的梁理论,可以得到梁的振动微分方程为
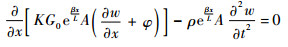 | (2) |
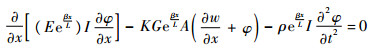 | (3) |
式中:w和φ分别为梁截面的横向变形和转角。
横截面弯曲力矩M和剪力Q可以表示为
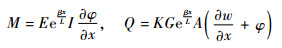 | (4) |
1.2 状态空间传递矩阵 直接由式(2)~式(4)无法得到传递矩阵为常数的状态方程,因此对结构的状态变量进行替换,令
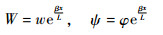 | (5) |
因此
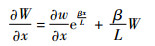 | (6) |
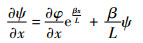 | (7) |
由式(6)、式(7)可以得到
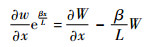 | (8) |
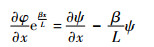 | (9) |
定义函数f(x)的傅里叶变换为
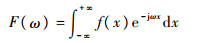 | (10) |
式中:ω为圆频率。
因此函数的傅里叶逆变换为
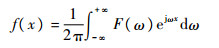 | (11) |
对式(2)~式(4)两端同时对时间t进行傅里叶变换,并将式(8)、式(9)代入式(2)~式(4)中并化简可以得到关于W、ψ、M和Q的状态空间方程:
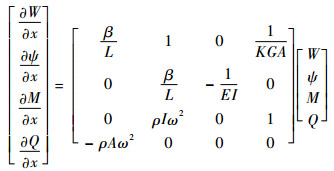 | (12) |
式(10)可以写成如下形式:
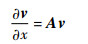 | (13) |
式中:v为状态向量;A为传递矩阵。
由精细积分法可以得到
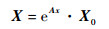 | (14) |
式中:X0为结构的初始状态向量。
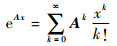 | (15) |
对于固支边界条件、简支边界条件和自由边界条件,依次有
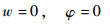 | (16) |
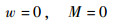 | (17) |
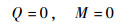 | (18) |
根据式(5)可以得到
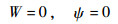 | (19) |
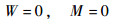 | (20) |
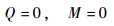 | (21) |
运用边界条件式(19)~式(21)和传递矩阵法[20]可以得到结构的频率方程,求解此频率方程可以得到不同边界条件下结构固有频率的精确解。
1.3 裂纹对结构局部柔度的影响 弹性结构表面的开口裂纹会使裂纹局部区域的应变能集中而造成结构局部柔度的增加,Attar[23]提出采用无质量的弹簧来模拟裂纹区域对结构局部柔度的贡献。图 2为圆形截面和矩形截面的表面裂纹示意图。裂纹平行于z轴,杆受到轴向载荷P1和剪力P2、P3,弯曲力矩P4、P5和扭转力矩P6,根据卡式定理可以得到裂纹区域产生的附加位移为
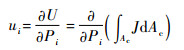 | (22) |
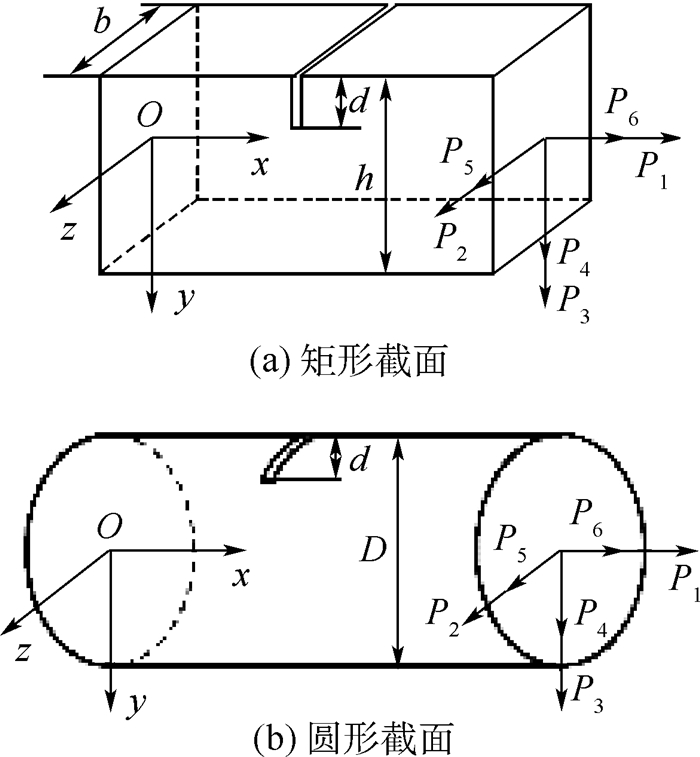 |
| 图 2 结构表面裂纹示意图 Fig. 2 Schematic diagram of structural surface crack |
| 图选项 |
式中:U为裂纹区域的应变能;Ac为裂纹区域;ui为沿力Pi方向裂纹所造成的附加位移;J为应变能密度函数[24],即
| $$ | (23) |
其中:υ为泊松比;平面应力状态下E′=E,平面应变状态下
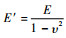
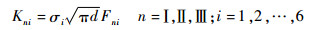 | (24) |
式中:σi为裂纹区域的应力;d为裂纹深度;Fni为与几何形状相关的裂纹形状因子。
因此,柔度系数可以定义为
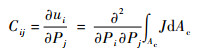 | (25) |
裂纹区域的柔度矩阵为6×6矩阵,由于本文仅考虑平面内的弯曲模态,对于平面弯曲模态,P5为式(25)的主要影响因素,因此对于平面弯曲模态的应力强度因子为
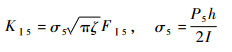 | (26) |
式中:ζ为沿裂纹宽度方向的坐标;h为矩形截面的深度。
因此,裂纹局部区域的柔度系数C55为[23]
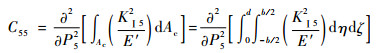 | (27) |
式中:b为裂纹的宽度;η为沿裂纹深度方向的坐标。
将式(26)代入式(27),并沿着裂纹的边界进行积分,矩形截面梁裂纹区域的局部柔度为[25]
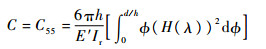 | (28) |
圆形截面梁裂纹区域的局部柔度为
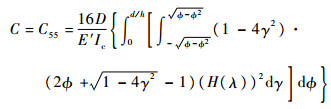 | (29) |
式中:Ir为矩形截面的惯性矩,Ir=bh3/12;D为圆形截面的直径;Ic=πD4/64为圆形截面的惯性矩;对于矩形截面?=ζ/D,对于圆形截面?=ζ/D;γ=η/D。
式(28)中,H(λ)可以表示为[25]
 | (30) |
式中:对于矩形截面,λ=?,对于圆形截面,λ可以表示为[25]
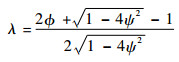 | (31) |
裂纹xc处的弹性模量
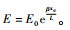
1.4 裂纹区域传递矩阵 裂纹两端的纵向位移、弯矩和剪力具有连续性,但是裂纹两端的转角却不存在连续性,本文采用扭转弹簧来模拟裂纹对结构局部柔度的贡献,裂纹所在位置的坐标为xc,因此有
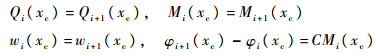 | (32) |
由式(32)可以得到裂纹两端传递矩阵为
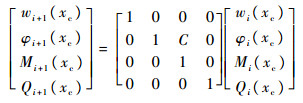 | (33) |
由式(5)和式(32)可以推出
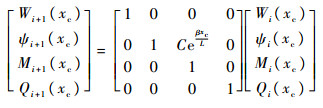 | (34) |
1.5 复杂边界条件多跨功能梯度Timoshenko梁振动模型 为了建立复杂边界条件下功能梯度Timoshenko梁的振动模型,考虑中间铰支座有k个,集中质量有n个,每个集中质量为mi(i=1, 2, …,n),转动惯量为Ji(i=1, 2, …,n)。拉压弹簧有m个,扭转弹簧有q个。对于考虑转动惯量的集中质量边界条件,集中质量的位置为xm,因此集中质量所在点满足:
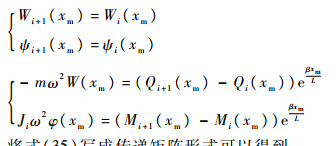 | (35) |
将式(35)写成传递矩阵形式可以得到
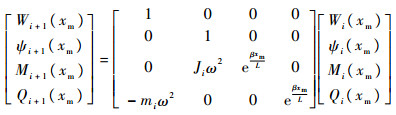 | (36) |
同理可以得到拉压弹簧的点传递矩阵H为
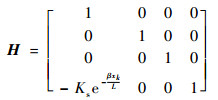 | (37) |
式中:xk为拉压弹簧的位置坐标;Ks为弹簧拉压刚度。
扭转弹簧的点传递矩阵H为
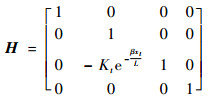 | (38) |
式中:Kt为扭转弹簧的刚度;xt为扭转弹簧的位置坐标。
中间铰支座的点传递矩阵H为
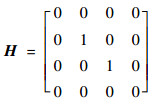 | (39) |
1.6 递推公式 功能梯度Timoshenko梁从一个边界条件到另一个边界条件经过一个力学元件和一段梁,梁段的场矩阵Hib由式(14)可以得到,力学元件的点传递矩阵为Hip,由此可以得到包含一段梁和一个力学元件的传递矩阵Hi:
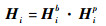 | (40) |
因此整个系统的传递矩阵可以表示为
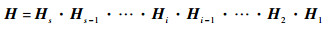 | (41) |
由推导可知,整个系统的传递矩阵H是一个4×4的矩阵,可以写成如下形式:
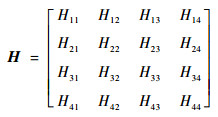 | (42) |
根据不同的边界条件,将式(42)代入式(19)~式(21),可以得到系统的频率方程F(ω)=0,求解上述频率方程可以得到复杂边界条件多跨功能梯度Timoshenko梁的频率精确解。
1.7 裂纹损伤识别
1.7.1 裂纹损伤识别方法 裂纹的存在会改变结构的频率方程F(ω)=0,并且对结构的模态振型与固有频率产生显著的影响。对于存在裂纹结构的损伤识别,裂纹的位置xi(i=1, 2, …,N)与深度di(i=1, 2…, N)均是需要识别的参数。由于结构的固有频率相对于模态振型的实验测试精度更高,因此本文采用固有频率对结构进行损伤识别。结构的固有频率可以通过模态实验测得。结构需要识别的参数有2N个,因此需要至少测得结构的前2N阶频率ωi(i=1, 2, …, 2N)。由结构的前2N阶频率可以获得关于损伤待识别参数的2N个非线性方程:
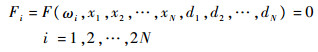 | (43) |
为了求解非线性方程组(43),Grosan和Abraham[26]将非线性方程(43)转化为多目标优化问题:
 | (44) |
转化为式(44)的目的是为了缩小等式左边与右边的残差,从而获得方程组(43)的解。然而,采用多目标优化的方法通常计算精度与效率较低。因此,Pourrajabian等[27]提出了一种新的求解非线性方程组的优化方法,即将非线性方程组转化为单一目标函数的约束优化问题。优化问题的目标函数为
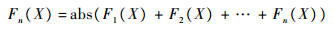 | (45) |
式中:X=(x1, x2, …, xN, d1, d2, …, dN)。
约束条件见式(43)。
为了将约束优化问题(43)转化为无约束的优化问题,采用增广拉格朗日算法[28],新的目标函数定义为
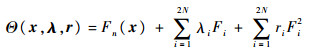 | (46) |
式中:系数λi为非负的拉格朗日乘子,可以由式(47)进行更新计算[29]:
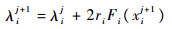 | (47) |
其中:j为循环次数;ri为正的罚参数,可以由式(48)进行更新运算:
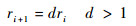 | (48) |
每更新一次参数λi和ri,便需要求解一次全局优化的子问题。
1.7.2 差分进化算法 启发式算法是一类求解全局优化的智能算法,具有较好的全局寻优能力,而在众多的启发式算法中,差分进化算法是一种基于群体差异的启发式随机搜索算法[30]。差分进化算法保留了基于种群的全局搜索策略,采用实数编码、基于差分的简单变异操作和一对一的竞争生存策略,降低了遗传操作的复杂性。同时,差分进化算法特有的记忆能力使其可以动态跟踪当前的搜索情况,以调整其搜索策略,具有较强的全局收敛能力和鲁棒性,且不需要借助问题的特征信息。同时,差分进化算法具有算法原理简单、受控参数少等特点。差分进化算法的进化流程为变异、交叉和选择。差分进化算法中的差分策略即通过采用个体间的差异(即差分向量)对个体进行扰动,实现个体的变异。对于优化问题:
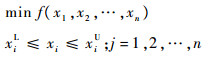 | (49) |
式中:n为解空间的维数;xiU为xi和xiL的取值范围的上下界。
差分进化算法的流程如下[20]:
1)?初始化种群。初始种群
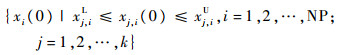 |
随机产生:
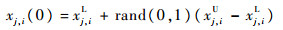 |
式中:xi(0)为种群中第0代的第i条染色体;xj, i(0)为第0代的第i条染色体的第j个基因;NP为种群大小;rand(0, 1)为在区间(0, 1)均匀分布的随机数。
2)?变异操作。差分进化算法通过差分策略实现个体变异,这是与遗传算法区别的重要标志。
在差分进化算法中,常见的差分策略是随机选取种群中的2个不同的个体,将向量差乘以缩放因子Ms并与待变异的个体进行向量合成:
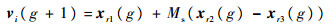 |
式中:xi(g)为第g代种群中第i个个体向量;vi(g+1)为新合成的向量。
在进化的过程中,通常为了使解满足约束条件,必须判断染色体中的各个基因是否满足边界条件,如果不满足边界条件,则基因采用与初始种群相同的随机生成方法。
第g代种群{xi(g)|xj, iL≤xj, i(0)≤xj, iU, i=1, 2, …, NP; j=1, 2, …, k},通过变异后产生一个中间体:
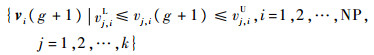 |
3)?交叉操作。将变异的中间体{vi(g+1)}和第g代种群{xi(g)}进行个体间的交叉操作:
 |
式中:CR为交叉概率;jrand为[1, 2, …, k]的随机整数。具体过程可以参见文献[20]。
4)?选择操作。差分进化算法通过采用贪婪算法来选择进入下一代种群的个体:
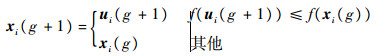 |
裂纹损伤识别方法流程如图 3所示。
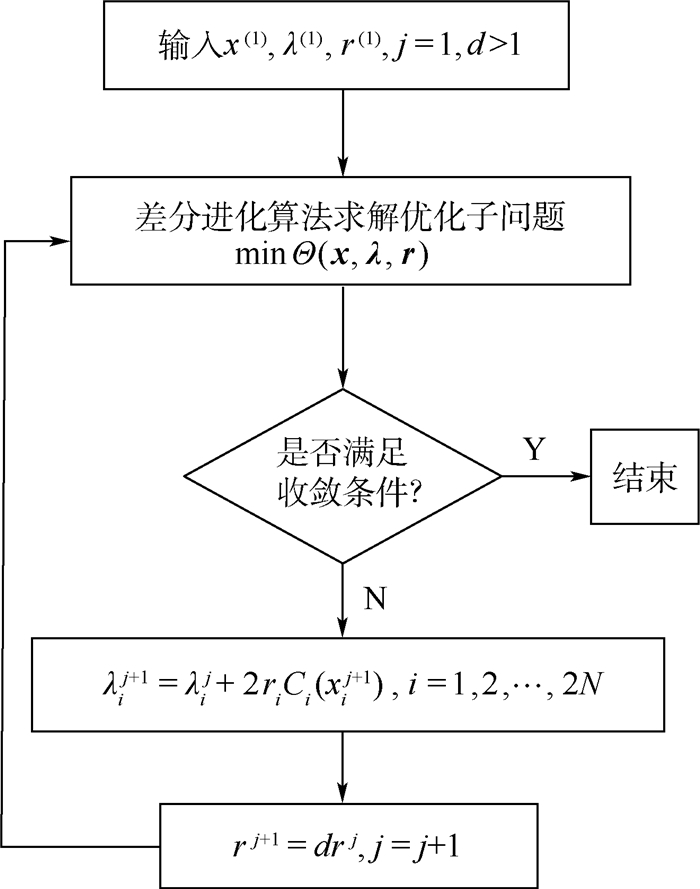 |
| 图 3 裂纹损伤识别方法 Fig. 3 Crack damage identification method |
| 图选项 |
2 算例 2.1 算例1 考虑截面为圆形的两端简支的功能梯度Timoshenko梁,圆形截面直径D=0.03 m,梁长L=5 m,弹性模量E0=71 GPa,剪切模量G0=27.31 GPa,密度ρ0=2 780 kg/m3,剪切系数K=0.9,梯度系数β=2,材料沿x方向指数分布。梁表面存在2处裂纹,裂纹的位置如图 4所示。其中,裂纹1的横坐标x1=0.2 L,裂纹深度d1=0.5 D;裂纹2的横坐标x2=0.8 L,裂纹深度d2=0.2 D。裂纹损伤识别方法中,初始拉格朗日乘子λ(1)=1,初始的罚参数r(1)=10。裂纹损伤识别方法迭代过程如图 5所示。表 1~表 3分别表示损伤识别输入频率和裂纹位置与裂纹深度的识别结果。
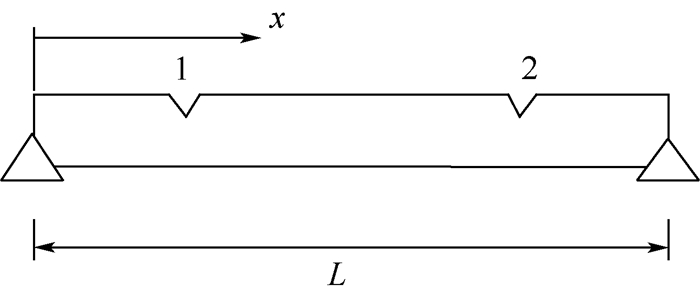 |
| 图 4 简支边界条件下存在裂纹的功能梯度Timoshenko梁 Fig. 4 Functionally graded Timoshenko beam with cracks under simple-supported boundary conditions |
| 图选项 |
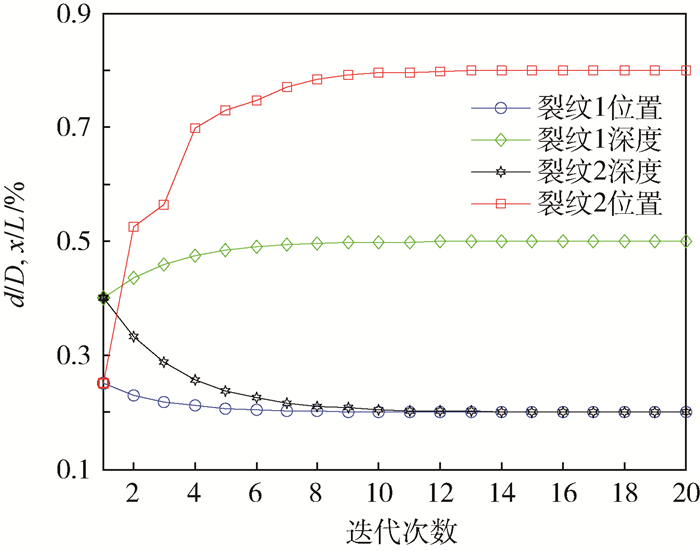 |
| 图 5 简支边界条件下裂纹损伤识别方法迭代过程 Fig. 5 Iterative process of crack damage identification method under simple-supported boundary conditions |
| 图选项 |
表 1 简支边界条件下损伤识别输入频率 Table 1 Damage identification input frequency under simple-supported boundary conditions
| Hz | ||||
| 实测输入频率 | ω1 | ω2 | ω3 | ω4 |
| 数值 | 22.122 5 | 60.160 5 | 116.978 8 | 192.100 1 |
表选项
表 2 简支边界条件下裂纹位置x/L识别结果 Table 2 Identification results of crack position x/L under simple-supported boundary conditions
| 裂纹 | 实际值 | 初始值 | 辨识结果 | 误差/% |
| 裂纹1 | 0.20 | 0.25 | 0.201 45 | 0.725 |
| 裂纹2 | 0.80 | 0.25 | 0.796 33 | 0.459 |
表选项
表 3 简支边界条件下裂纹深度d/D识别结果 Table 3 Identification results of crack depth d/D under simple-supported boundary conditions
| 裂纹 | 实际值 | 初始值 | 辨识结果 | 误差/% |
| 裂纹1 | 0.5 | 0.4 | 0.499 46 | 0.108 |
| 裂纹2 | 0.2 | 0.4 | 0.200 18 | 0.090 |
表选项
2.2 算例2 复杂边界条件下多跨功能梯度Timoshenko梁如图 6所示。铰支座位于L/2处。矩形截面尺寸D=0.03 m,梁长L=5 m,弹性模量E0=71 GPa,剪切模量G0=27.31 GPa,密度ρ0=2 780 kg/m3,剪切系数K=0.9,材料沿x方向指数分布,梯度系数β=2,附加质量块的质量与转动惯量为m=1 kg, J=0.125 kg·m2。梁表面存在2处裂纹,如图 6所示。裂纹损伤识别方法中,初始拉格朗日乘子λ(1)=1.5,初始的罚参数r(1)=10。裂纹损伤识别方法迭代过程如图 7所示。表 4~表 6分别表示损伤识别输入频率和裂纹位置与裂纹深度的识别结果。
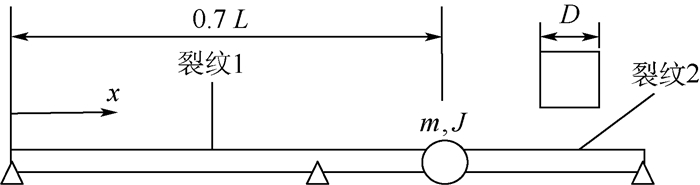 |
| 图 6 复杂边界条件下存在裂纹的功能梯度Timoshenko梁 Fig. 6 Functionally graded Timoshenko beam with cracks under complex boundary conditions |
| 图选项 |
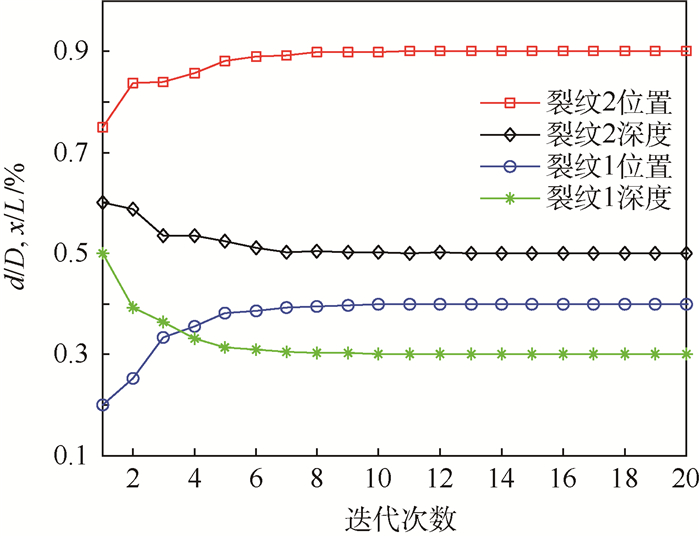 |
| 图 7 复杂边界条件下裂纹损伤识别方法迭代过程 Fig. 7 Iterative process of crack damage identification method under complex boundary conditions |
| 图选项 |
表 4 复杂边界条件下损伤识别输入频率 Table 4 Damage identification input frequencyunder complex boundary conditions
| Hz | ||||
| 实测输入频率 | ω1 | ω2 | ω3 | ω4 |
| 数值 | 32.785 9 | 42.335 2 | 148.491 6 | 156.130 9 |
表选项
表 5 复杂边界条件下裂纹位置x/L识别结果 Table 5 Identification results of crack position x/L under complex boundary conditions
| 裂纹 | 实际值 | 初始值 | 辨识结果 | 误差/% |
| 裂纹1 | 0.40 | 0.20 | 0.401 25 | 0.312 5 |
| 裂纹2 | 0.90 | 0.75 | 0.890 11 | 1.098 9 |
表选项
表 6 复杂边界条件下裂纹深度d/D识别结果 Table 6 Identification results of crack depth d/D under complex boundary conditions
| 裂纹 | 实际值 | 初始值 | 辨识结果 | 误差/% |
| 裂纹1 | 0.3 | 0.5 | 0.293 01 | 2.330 |
| 裂纹2 | 0.5 | 0.6 | 0.490 11 | 1.978 |
表选项
3 结论 本文通过变量替换得到了一组新的状态空间变量,通过状态空间理论得到了功能梯度Timoshenko梁的传递矩阵。
1)?所使用的状态空间传递矩阵法物理概念清晰,通过状态空间变量的替换,不但降低了问题的求解难度,而且减少了计算量。
2)?分析了裂纹对结构局部柔度的影响,推导了裂纹区域的传递矩阵,建立了表面存在裂纹的功能梯度Timoshenko梁的解析模型。
3)?建立了复杂边界条件下多跨功能梯度Timoshenko梁的解析模型。
4)?结构裂纹损伤识别方法中,将多目标优化问题转化为单一目标优化问题,通过采用增广拉格朗日算法与差分进化算法的结合对功能梯度Timoshenko梁进行损伤识别,计算结果表明,识别精度较高。
参考文献
| [1] | BIRMAN V, BYRD L W. Modeling and analysis of functionally graded materials and structures[J].Applied Mechanics Reviews, 2007, 60(1-6): 195–216. |
| [2] | ZHONG Z, YU T. Analytical solution of a cantilever functionally graded beam[J].Composites Science and Technology, 2007, 67(3-4): 481–488.DOI:10.1016/j.compscitech.2006.08.023 |
| [3] | LI X F. A unified approach for analyzing static and dynamic behaviors of functionally graded Timoshenko and Euler-Bernoulli beams[J].Journal of Sound and Vibration, 2008, 318(4-5): 1210–1229.DOI:10.1016/j.jsv.2008.04.056 |
| [4] | LI X F, WANG B L, HAN J C. A higher-order theory for static and dynamic analyses of functionally graded beams[J].Archive Applied Mechanics, 2010, 80(10): 1197–1212.DOI:10.1007/s00419-010-0435-6 |
| [5] | PRADHAN K K, CHAKRAVERTY S. Free vibration of Euler and Timoshenko functionally graded beams by Rayleigh-Ritz method[J].Composites Part B:Engineering, 2013, 51: 175–184.DOI:10.1016/j.compositesb.2013.02.027 |
| [6] | KANG Y A, LI X F. Large deflections of a non-linear cantilever functionally graded beam[J].Journal of Reinforced Plastics and Composites, 2010, 29(12): 1761–1774.DOI:10.1177/0731684409103340 |
| [7] | ELISHAKOFF I. Eigenvalues of inhomogeneous structures:Unusual closed-form solutions[M].Boca Raton: CRC Press, 2005: 284-285. |
| [8] | ECE M C, AYDOGDU M, TASKIN V. Vibration of a variable cross-section beam[J].Mechanics Research Communications, 2007, 34(1): 78–84.DOI:10.1016/j.mechrescom.2006.06.005 |
| [9] | ATMANE H A, TOUNSI A, MEFTAH S A, et al. Free vibration behavior of exponentially functionally graded beams with varying cross-section[J].Journal of Vibration and Control, 2011, 17(2): 311–318.DOI:10.1177/1077546310370691 |
| [10] | WANG C Y, WANG C M. Exact vibration solutions for a class of nonuniform beams[J].Journal of Engineering Mechanics, 2013, 139(7): 928–931.DOI:10.1061/(ASCE)EM.1943-7889.0000535 |
| [11] | WANG C Y, WANG C M. Exact vibration solution for exponentially tapered cantilever with tip mass[J].Journal of Vibration and Acoustics, 2012, 134(4): 041012.DOI:10.1115/1.4005835 |
| [12] | SANKAR B V. An elasticity solution for functionally graded beams[J].Composites Science and Technology, 2001, 61(5): 689–696.DOI:10.1016/S0266-3538(01)00007-0 |
| [13] | ESMAILZADEH E, OHADI A. Vibration and stability analysis of non-uniform Timoshenko beams under axial and distributed tangential load[J].Journal of Sound and Vibration, 2000, 236(3): 443–456.DOI:10.1006/jsvi.2000.2999 |
| [14] | HUANG Y, YANG L E, LUO Q Z. Free vibration of axially functionally graded Timoshenko beams with non-uniform cross-uniform cross-section[J].Composites Part B:Engineering, 2013, 45(1): 1493–1498.DOI:10.1016/j.compositesb.2012.09.015 |
| [15] | LI X F, KANG Y A, WU J X. Exact frequency equations of free vibration of exponentially functionally graded beams[J].Applied Acoustics, 2013, 74(3): 413–420.DOI:10.1016/j.apacoust.2012.08.003 |
| [16] | TANG A Y, WU J X, LI X F. Exact frequency equations of free vibration of exponentially non-uniform functionally graded Timoshenko beams[J].International Journal of Mechanical Sciences, 2014, 89: 1–11.DOI:10.1016/j.ijmecsci.2014.08.017 |
| [17] | YOKOYAMA T, CHEN M C. Vibration analysis of edge-cracked beams using a line-spring model[J].Engineering Fracture Mechanics, 1998, 59(3): 403–409.DOI:10.1016/S0013-7944(97)80283-4 |
| [18] | SHIFRIN E I, RUOTOLO R. Natural frequencies of a beam with arbitrary number of cracks[J].Journal of Sound and Vibration, 1999, 222(3): 409–423.DOI:10.1006/jsvi.1998.2083 |
| [19] | LI Q S. Buckling of muti-step cracked columns with shear deformation[J].Engineering Structures, 2001, 23(4): 356–364.DOI:10.1016/S0141-0296(00)00047-X |
| [20] | HSU M H. Vibration analysis of edge-cracked beam on elastic foundation with axial loading using the differential quadrature method[J].Computer Methods in Applied Mechanics and Engineering, 2005, 194(1): 1–17.DOI:10.1016/j.cma.2003.08.011 |
| [21] | YANG J, CHEN Y, XIANG Y, et al. Free and forced vibration of cracked inhomogeneous beams under an axial force and a moving load[J].Journal of Sound and Vibration, 2008, 312(1-2): 166–181.DOI:10.1016/j.jsv.2007.10.034 |
| [22] | WEI D, LIU Y H, XIANG Z H. An analytical method for free vibration analysis of functionally graded beams with edge cracks[J].Journal of Sound and Vibration, 2012, 331(7): 1686–1700.DOI:10.1016/j.jsv.2011.11.020 |
| [23] | ATTAR M. A transfer matrix method for free vibration analysis and crack identification of stepped beams with multiple edge cracks and different boundary conditions[J].International Journal of Mechanical Sciences, 2012, 57(1): 19–33.DOI:10.1016/j.ijmecsci.2012.01.010 |
| [24] | TADA H, PARIS P C, IRWIN G R. The stress analysis of cracks handbook[M].New York: ASME Press, 2000: 164. |
| [25] | NARKIS Y, ELMALAH E. Crack identification in a cantilever beam under uncertain end conditions[J].International Journal of Mechanical Sciences, 1996, 38(5): 499–507.DOI:10.1016/0020-7403(95)00071-2 |
| [26] | GROSAN C, ABRAHAM A. A new approach for solving nonlinear equations systems[J].IEEE Transactions on Systems, Man, and Cybernetics, Part A:Systems and Humans, 2008, 38(3): 698–714.DOI:10.1109/TSMCA.2008.918599 |
| [27] | POURRAJABIAN A, EBRAHIMI R, MIRZAEI M, et al. Applying genetic algorithms for solving nonlinear algebraic equations[J].Applied Mathematics and Computation, 2013, 219(24): 11483–11494.DOI:10.1016/j.amc.2013.05.057 |
| [28] | CONN A R, GOULD N I M, TOINT P L. A globally convergent augmented Lagrangian algorithm for optimization with general constraints and simple bounds[J].SIAM Journal on Numerical Analysis, 1991, 28(2): 545–572.DOI:10.1137/0728030 |
| [29] | HESTENES M R. Multiplier and gradient methods[J].Journal of Optimization Theory and Applications, 1969, 4(5): 303–320.DOI:10.1007/BF00927673 |
| [30] | 杨启文, 蔡亮, 薛云灿. 差分进化算法综述[J].模式识别与人工智能, 2008, 21(4): 507–513.YANG Q W, CAI L, XUE Y C. A survey of differential evolution algorithms[J].Pattern Recognition and Artificial Intelligence, 2008, 21(4): 507–513.(in Chinese) |
