增强型开关电感准Z源逆变器<sup>*</sup> - 北京航空航天大学论文文献

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

增强型开关电感准Z源逆变器^*

本站小编 Free考研考试/2021-12-25

在光伏发电系统中，由于受光照强度、光照时间和环境温度等一系列因素的影响，使得电池电压在大范围内变化；电池电压输入等级低，给逆变带来一定的困难。因此，需要输入电压可在大范围内变化且具有高升压能力的新型逆变器。Z源逆变器^[1]自提出以来，凭借其独特的网络结构优势，受到了中外****的关注，从而推动了Z源逆变器的飞速发展。虽然传统Z源逆变器与普通逆变器^[2-6]相比有着诸多优势，然而其也有相应的缺点：升压比不显著，LC网络电容应力大，输入电流断续等，限制了Z源逆变器在实际中的应用。汤雨等^[7]通过互换逆变桥和功率二极管的位置来达到抑制启动冲击的目的，然而升压能力也是Z源逆变器的一个重要内容。Gajanayake和Tang^[8-10]等为了提高升压能力，用级联的方式提高直流侧的升压能力，虽然使得升压能力得到提高，但升压能力有限。Zhu等^[11]首次利用开关电感技术，大幅提高了升压能力，但是缺点也很明显：LC网络电流断续，电容两端承压高，电路启动瞬间电流大。Nguyen等^[12]提出了开关电感Ⅰ型准Z源逆变器，很好地解决了Zhu等^[11]所提拓扑存在的问题，升压比方面有一定程度的提高，但依然不够。邓凯等^[13]将开关电感Ⅰ型准Z源逆变器中的二极管用一个自举电容来代替，提出了开关电感Ⅱ型准Z源逆变器，该型逆变器升压能力相比于Ⅰ型拓扑结构较高，但是升压能力依然达不到实际需求。
为了满足以上要求，本文提出了一种增强型开关电感准Z源逆变器。该增强型拓扑结构在邓凯等^[13]研究的基础上将电感L₁用开关电感支路代替，并在此基础上增加了2个电感和3个二极管。本文给出了增强型开关电感准Z源逆变器的通用型式(N组开关电感)。在实际应用中，虽然增加开关电感的组数必然会提高直流链升压比，但过多增加开关电感组数会导致调制因子过大(M＞0.9)，直通占空比(D_sh＜0.1)的取值范围过窄，导致逆变器交流输出电压幅值降低；而且过多的开关电感组数会导致硬件电路变得过于复杂，硬件成本增高等问题，限制了增强型开关电感准Z源逆变器的应用。本文提出的增强型拓扑结构的升压能力可满足大多数的升压要求。故本文以2重开关电感数为拓扑，详细介绍其相关性能(以下简称增强型拓扑)。
1 增强型拓扑工作原理本文提出的增强型拓扑结构如图 1所示，该拓扑结构由5个电感和3个电容组成。图 1中：D₁-D₂-D₃-D₄-D₅-D₆-L₁-L₂-L₃组成第1组电感单元，D₇-D₈-L₄-L₅-C₃组成第2组电感单元；U_in为电池输入直流电压；U_PN为直流链电压。

图 1 增强型拓扑结构示意图 Fig. 1 Schematic diagram of enhanced topology structure

图选项

与开关电感Ⅱ型准Z源逆变器拓扑相比，增强型拓扑增加了一组开关电感单元，并在此基础上新增加了3个二极管和1个电感(D₄、D₅、D₆和L₃)，从而使得拓扑的升压能力得到进一步提高。当3桥臂工作在直通状态时，逆变桥等效为一根短接导线，该状态称为直通状态；反之，逆变桥等效为电流源，并称该状态为非直通状态。具体工作过程如下：
1) 直通状态。直通状态下，拓扑等效电路如图 2所示。为了简化分析，所有元器件均为理想器件，且C₁=C₂=C₃=C,L₁=L₂=L₃=L₄=L₅=L。直通状态下，支路1中二极管D₁、D₃、D₄由于承受正向电压导通，D₂、D₅承受反向电压断开，从而使得电感L₁、L₂、L₃并联，电容C₂和电源共同为这3个并联电感充电。同理，支路2中二极管D₇、D₈导通，从而使得电感L₄、L₅并联，电容C₁和电源共同为这2个并联电感充电。

图 2 直通状态下的等效电路 Fig. 2 An equivalent circuit in shoot-through state

图选项

由基尔霍夫电压定律，图 2所示拓扑的电路方程为

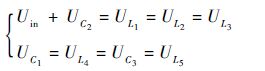(1)

式中：U_C₁、U_C₂和U_C₃分别为电容C₁、C₂和C₃的电压；U_L₁、U_L₂、U_L₃、U_L₄和U_L₅分别为L₁、L₂、L₃、L₄和L₅两端电压。
2) 非直通状态。非直通状态下，其等效电路如图 3所示。在非直通状态下，支路1中的二极管D₁、D₃、D₄反向断开，D₂、D₅正向导通，从而使得电感L₁、L₂、L₃串联。同理，支路2中二极管D₇、D₈反向关断，从而使得电感L₄、L₅串联。电感L₁、L₂、L₃、L₄、L₅及电容C₃向电容C₁、C₂及负载充电。

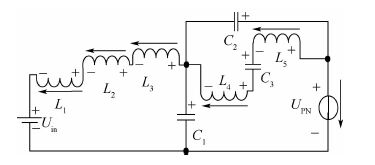图 3 非直通状态下的等效电路 Fig. 3 An equivalent circuit in non shoot-through state

图选项

由图 3得出此状态下的电路方程为

(2)

由式(1)可知，电感L₁两端电压为

(3)

由式(2)可知，电感L₁两端电压为

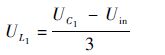(4)

由伏秒平衡原理可知，稳态时单周期内电感两端的平均电压为0，由式(3)、式(4)可得

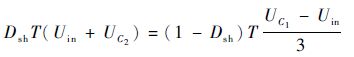(5)

式中：T为开关管一个开关周期。
化简式(5)后得到

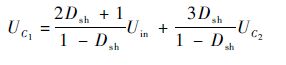(6)

同理，在直通状态下，L₄两端电压为：U_L₄=U_L₅=U_C₃；非直通状态下，L₄两端电压为：U_L₄=(U_C₂-U_C₃)/2，根据伏秒平衡原理得到

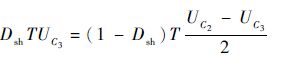(7)

化简式(7)可得

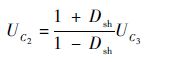(8)

在一个开关周期内，由于电容电压不能突变，可以假定电容为一个电压源，则由式(1)可知

(9)

将式(8)和式(9)代入式(6)，得到

(10)

化简式(10)得到

(11)

同理，可以推出U_C₂和U_PN,即

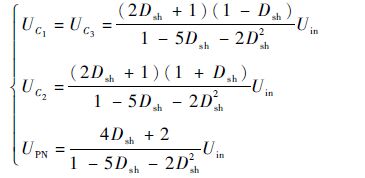(12)

由式(12)可知，升压因子B为

(13)

当B≥1时，实现升压能力，即

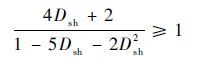(14)

求出不等式(14)的解可知，当直通占空比D_sh＜0.186时，升压因子B＞1,从而实现升压。图 4给出了增强型拓扑和Ⅰ型、Ⅱ型拓扑相应的关系曲线。

图 4 增强型拓扑与传统结构的升压能力对比 Fig. 4 Comparison of boost ability between enhancedtopology and traditional topology

图选项

式(12)是以第1组电感单元的2组开关电感所组成结构的相关表达式，以此为例，可以求出第一组电感单元的开关电感数为N组时，相关电容电压、直流链电压等参数的通用型式，也即增强型拓扑的通用型式，即

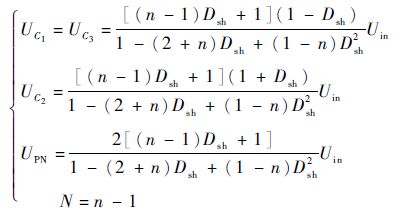(15)

式中：n为第1组电感单元的开关电感组数中电感的个数。
由式(15)可以发现，随着开关电感组数N的增加，直通占空比随之减小，调制因子随之变大，使得输出交流电压幅值降低，这就需要在直流链升压比和输出交流电压幅值之间做出取舍，以达到最佳的系统平衡点。
2 元器件电压电流应力分析本文采用基于SVPWM的控制策略，文献^[14]指出，相比于文献^[15-16]所提的两种控制策略，最大恒定升压SVPWM控制的直通时间最长，升压能力最高；直通时间恒定，有利于直流链电压的稳定，降低控制难度；开关频率降低，有利于减小电感电流纹波。因此，下文如不特别说明，均采用最大恒定升压控制策略。假定逆变系统的电源电压和直流链电压均相同。由文献^[14]可知，直通占空比D_sh和调制因子M的关系表示为

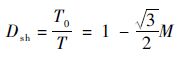(16)

式中：T₀为逆变桥直通时间。
将式(16)代入式(12)中，得到增强型拓扑的升压因子B、调制因子M以及电压增益G的关系式为

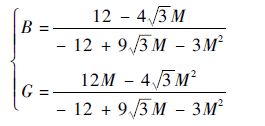(17)

由式(16)和式(17)可以导出增强型拓扑的直通占空比D_sh与电压增益G之间的关系，即

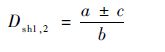(18)

式中：

(19)

由于直通占空比D_sh∈[0, 1]，故

舍去。从而D_sh与G的关系为

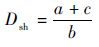
(20)

设定U_C₁₁、U_C₁₂和U_C₁₃分别为增强型拓扑、Ⅱ型拓扑和Ⅰ型拓扑中的电容C₁的电压应力。将式(20)代入式(12)，得到

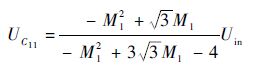(21)

式中：

。
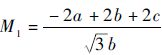
同样的，由文献^[12-13]可知，U_C₁₂和U_C₁₃分别为

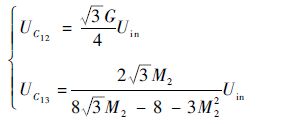(22)

式中：

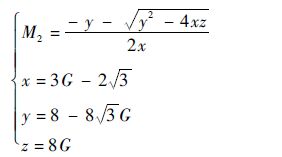(23)

与上述方法类似，可求出增强型拓扑、Ⅱ型拓扑和Ⅰ型拓扑3种拓扑结构电容C₂的电压应力为

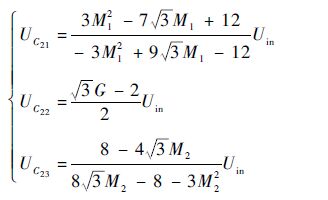(24)

由式(21)、式(22)、式(24)可以得到3种拓扑结构在同等条件下的电容电压应力的比较，如图 5所示。图中：U_{C_i}为电容电压，i=1,2,3。

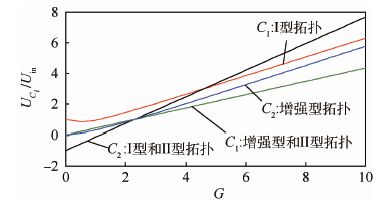图 5 3种拓扑U_{C_i}/U_in与电压增益G的关系 Fig. 5 Relationships between U_{C_i}/U_in and voltagegain G of three kinds of topologies

图选项

由图 5可知，增强型拓扑电容C₁与Ⅱ型拓扑电容C₁的电压应力相同，Ⅰ型拓扑电容C₁的电压应力最高。增强型拓扑电容C₂的电压应力低于Ⅰ型和Ⅱ型拓扑电容C₂的电压应力，尤其是电压增益G在区间^{[8, 10]}里，电容电压应力明显低于其他两种拓扑的电容电压应力，此时Ⅱ型和Ⅰ型拓扑电容电压应力相同。
由图 2及式(12)可知，电感两端的电压为

(25)

式中：i_L₁为电感L₁上的电流值。
电感两端电流在一个单位周期内的脉动可表示为

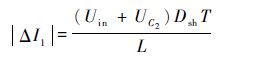(26)

将式(12)中U_C₂与U_in的关系代入式(26)中，得到增强型拓扑的电感L₁上电流脉动 ΔI₁₁ 为

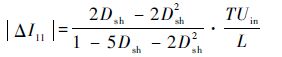(27)

将式(27)中直通占空比用电压增益M₁来表示，可得到M₁与电流脉动的关系为

(28)

同理，由文献^{[14, 16]}可知，Ⅱ型和Ⅰ型拓扑的电流脉动分别为 ΔI₁₂ 和 ΔI₁₃ ,由电压增益G表示为

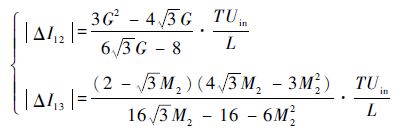(29)

由式(28)、式(29)可知，不同拓扑的电流脉动 ΔI_1i 可以表示为

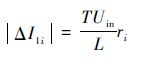(30)

式中：r_i为电流脉动系数，i=1,2,3。
从而本文提到的3种拓扑的电流脉动系数r_i分别为

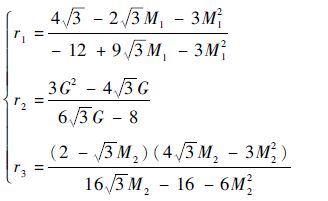(31)

由式(30)、式(31)可以得到3种拓扑结构在同等条件下的电感电流脉动的比较，如图 6所示。

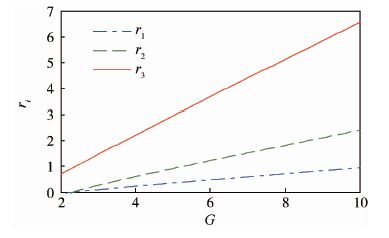图 6 3种拓扑电流脉动系数r_i与电压增益G的关系 Fig. 6 Relationships between current ripple factor r_i andvoltage gain G of three kinds of topologies

图选项

由图 6可知，增强型拓扑的电感电流脉动小于Ⅰ型、Ⅱ型拓扑的电感电流脉动，在电压增益区间^{[8, 10]}里，增强型拓扑电流脉动系数明显小于其他两种拓扑的电流脉动系数。
由文献^[17-18]可知，在逆变电路中，直流链电压U_PN决定了逆变桥中的6个开关管所承受的电压等级。即使控制策略和电压增益G相同，不同拓扑的逆变器直流链电压U_PN也不一定相同。用电压增益以及调制因子来表示输入电压与直流链电压的关系，即

(32)

式中：U_PN₁、U_PN₂和U_PN₃分别为增强型拓扑、Ⅱ型拓扑和Ⅰ型拓扑的逆变器侧的直流链电压。
由式(32)可以得到3种拓扑结构在相同的控制策略及输入输出条件下的逆变器侧直流链电压的比较，如图 7所示。

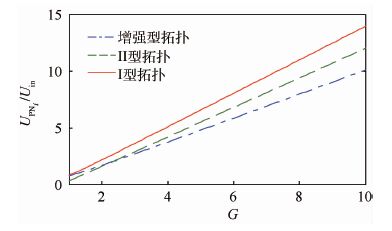图 7 3种拓扑U_{PN_i}/U_in与电压增益G的关系 Fig. 7 Relationships between U_{PN_i}/U_in and voltage gain G of three kinds of topologies

图选项

由图 7可知，在电压增益G∈(2，10)的区间里，相较于其他两种拓扑结构，增强型拓扑的逆变器侧直流链电压最低，从而降低了器件的电压应力，有利于选择电压应力较小的开关器件。
3 仿真结果分析在对增强型开关电感准Z源逆变器进行详细理论分析的基础上，为了验证相关理论分析的正确性，本文在MATLAB/Simulink仿真软件里搭建了增强型拓扑的仿真模型。仿真所用参数设置如表 1所示。
表 1 仿真参数 Table 1 Parameters of simulation system

参数	数值
准Z源网络电感L₁,L₂,L₃,L₄,L₅/mH	1
准Z源网络电容C₁,C₂,C₃/μF	1 000
直流电压源U_in/V	48
输出滤波电感L_f/mH	1
输出滤波电容C_f/μF	20
载波频率f/kHz	10

表选项

图 8分别为增强型、Ⅱ型和Ⅰ型拓扑的输出电压波形。图 8所示的逆变器侧直流链电压分别为U_PN₁=550 V，U_PN₂=240 V，U_PN₃=120 V。由此可以看出，本文提出的增强型拓扑较其他两种拓扑的升压能力更强；且增强型拓扑在逆变桥都不导通的工况下，X型网络中的电感、电容就不存在启动充电回路，从而防止电路启动瞬间烧毁电路。由图 8可知，增强型拓扑直流链电压由低到高渐渐达到稳定；而其他两种拓扑则是由高到低渐渐达到稳定，从而验证了该两种拓扑启动时存在启动冲击的问题。

图 8 3种拓扑的逆变器侧直流链电压的仿真波形 Fig. 8 Simulation waveforms of inverter DC link voltagesunder three kinds of topologies

图选项

图 9、图 10为3种不同结构的拓扑在输入电压为48 V、输出相电压为120 V、采用最大恒定升压控制策略的状态下，在相同的电压增益G下的电容C₁、C₂两端电压以及电感L₁两端电流的波形。

图 9 电容电压仿真对比波形 Fig. 9 Comparison of capacitor voltage simulation waveforms

图选项

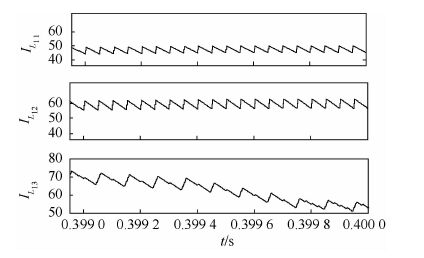图 10 电感电流仿真对比波形 Fig. 10 Comparison of inductor current simulation waveforms

图选项

图 9为3种拓扑电容C₁、C₂电压应力的仿真结果。可以看出，增强型拓扑结构的电容C₁的电压应力虽与Ⅱ型拓扑电容C₁的电压应力持平，但是低于Ⅰ型拓扑；在电容C₂电压应力方面，增强型拓扑低于Ⅰ型和Ⅱ型拓扑，Ⅰ型和Ⅱ型拓扑的电容C₂的电压应力基本持平。
图 10为3种拓扑电感L₁的电流脉动仿真波形。图中：I_L₁i(i=1,2,3)分别为增强型拓扑、Ⅱ型拓扑、Ⅰ型拓扑的电感电流。从图 10中可以看出，I_L₁₁值相比于其他电流脉动最小；I_L₁₂次之；I_L₁₃最高。从而增强型拓扑的电流质量最好。
4 实验验证在理论和仿真的基础上，对增强型拓扑进行实验验证，其中实验参数和仿真参数一致(见表 1)。
图 11为最大恒定控制策略下增强型拓扑的实验结果。其中，输出相电压为120 V。图中：左侧箭头为各个物理量的参考零点。从图 11(b)中可以看出，U_PN=480 V，U_C₁=200 V，U_C₂=320 V。由实验数值可知，实验结果和理论分析以及仿真有一些差距，但是基本一致。这主要是由于实际电路中存在器件的导通压降、线路的阻抗以及电磁干扰等因素影响。从而验证了本文的理论和仿真分析。

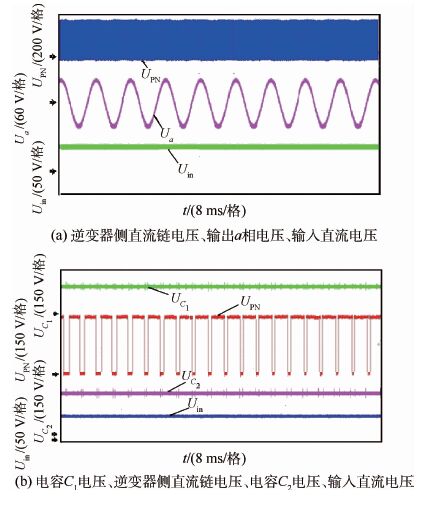图 11 增强型拓扑的相关实验波形 Fig. 11 Related experimental waveforms of enhanced topology

图选项

图 12、图 13为最大恒定控制策略下3种拓扑在相同的电压增益下增强型拓扑的实验结果。从图 12中可以看出，增强型拓扑、Ⅱ型拓扑、Ⅰ型拓扑的直流链电压分别为U_PN₁=200 V，U_PN₂=250 V，U_PN₃=270 V,从而增强型拓扑在直流链电压方面明显低于后两种拓扑。图 13为3种拓扑的电容电压及电感电流脉动的实验波形。3种拓扑的相关参数见表 2所示。

图 12 逆变器侧直流链电压的实验波形对比 Fig. 12 Comparison of experimental waveforms of inverter DC link voltages

图选项

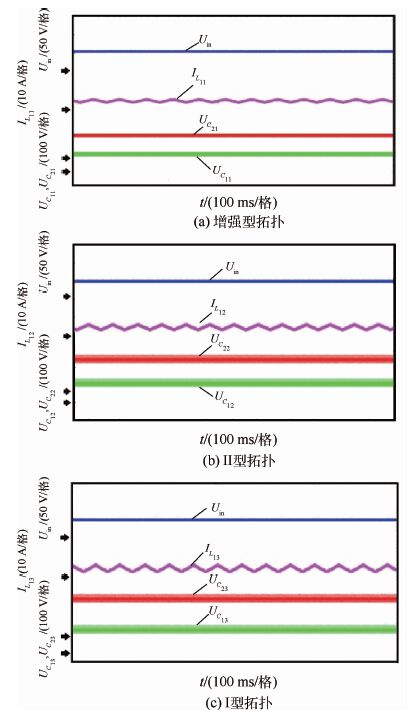图 13 电容电压及电感电流脉动的实验波形对比 Fig. 13 Comparison of experimental waveforms of capacitorvoltages and inductor current rippers

图选项

表 2 系统实验结果 Table 2 Experimental results of system

拓扑	U_C₁X/V	U_C₂X/V	电感电流/A
增强型拓扑	U_C₁₁=100	U_C₂₁=120	3
Ⅱ型拓扑	U_C₁₂=110	U_C₂₂=200	4
Ⅰ型拓扑	U_C₁₃=160	U_C₂₃=200	5

表选项

通过图 13中3种拓扑结构的实验波形可以发现，本文提出的增强型拓扑的电容C₁、C₂的电压应力以及电感电流的脉动均为最低，从而验证了理论和仿真的分析。
5 结论本文在邓凯等^[13]研究的基础上，对X型网络中的第1组电感单元进行了局部的改进优化，提出了一种新型的Z源逆变器拓扑。在对新型Z源逆变器拓扑的工作原理进行深入分析的基础上，对其电容、电感的电压电流应力以及直流链电压等级做了理论仿真分析，并以实验结果论证了理论仿真的正确性；在此基础上与其他开关电感准Z源逆变器拓扑进行了分析对比，从而增强型拓扑的优点总结如下：
1) 在同等直通占空比下，相较于其他Z源拓扑，增强型拓扑的升压比最高，并且远高于其他拓扑，为其在低压输入场合的广泛应用奠定了基础，具有很高的工程应用价值^[19]。
2) Z源网络的电容电压应力较小，使得电容在硬件选择上可以有更多的选择，这就给硬件设计带来了方便，电压等级降低，电容的体积、价格相应降低；电流脉动系数较小，提高直流链电能质量，减小控制回路的控制难度，简化控制算法。
3) 在相同的输出电压情况下，增强型拓扑可以获得更高的调制因子，从而使得电路中元器件的电压应力得到有效降低，进而使得硬件器件的选型得到简化。虽然增强型拓扑在升压比方面做了改进，但不可一味地追求升压比，要综合考虑实际运用场合，并且随着开关电感组数的增加，如何平衡直通占空比和调制因子之间的限制关系以及如何简化硬件电路，有待于进一步深入研究。

参考文献

[1]	PENG F Z. Z-source inverter[J].IEEE Transactions on Industry Applications, 2003, 39(2): 504–510.DOI:10.1109/TIA.2003.808920

[2]	彭方正, 房绪鹏, 顾斌, 等. Z 源变换器[J].电工技术学报, 2004, 19(2): 47–51.PENG F Z, FANG X P, GU B, et al. Z-source converter[J].Transactions of China Electrotechnical Society, 2004, 19(2): 47–51.(in Chinese)

[3]	刘和平, 刘平, 胡银全, 等. 改善电动汽车动力性能的双向Z源逆变器控制策略[J].电工技术学报, 2012, 27(2): 139–145.LIU H P, LIU P, HU Y Q, et al. Control scheme of bi-directional Z-source inverter in improving the dynamic performance of electrical vehicles[J].Transactions of China Electrotechnical Society, 2012, 27(2): 139–145.(in Chinese)

[4]	张筱文, 郑建勇, 尤錾, 等. 适用于大功率场合的新型双Z 源电压源逆变器[J].电网技术, 2011, 35(2): 25–31.ZHANG X W, ZHENG J Y, YOU J, et al. A novel double Z-source voltage source inverter suitable to high-power application scenarios[J].Power System Technology, 2011, 35(2): 25–31.(in Chinese)

[5]	张超华, 汤雨, 谢少军. 改进Z源逆变器的三次谐波注入控制策略[J].电工技术学报, 2009, 24(11): 114–119.ZHANG C H, TANG Y, XIE S J. Third harmonicinjection control strategy of improved Z-source inverter[J].Transactions of China Electrotechnical Society, 2009, 24(11): 114–119.(in Chinese)

[6]	周玉斐, 黄文新, 赵健伍. 一种高升压比的Z 源逆变器[J].电工技术学报, 2013, 28(9): 239–246.ZHOU Y F, HUANG W X, ZHAO J W. A high gain Z-source inverter[J].Transactions of China Electrotechnical Society, 2013, 28(9): 239–246.(in Chinese)

[7]	汤雨, 谢少军, 张超华. 改进型Z源逆变器[J].中国电机工程学报, 2009, 29(30): 28–34.TANG Y, XIE S J, ZHANG C H. Improved Z-source inverter[J].Proceedings of the Chinese Society for Electrical Engineering, 2009, 29(30): 28–34.(in Chinese)

[8]	TANG Y, XIE S J, ZHANG C H, et al. Improved Z-source inverter with reduced Z-source capacitor voltage stress and soft-start capability[J].IEEE Transactions on Power Electronics, 2009, 24(1-2): 409–415.

[9]	TANG Y, XIE S J, ZHANG C H. An improved Z-source inverter[J].IEEE Transactions on Power Electronics, 2011, 26(12): 3865–3868.DOI:10.1109/TPEL.2009.2039953

[10]	GAJANAYAKE C J, LUO F L, GOOI H B, et al. Extended-boost Z-source inverters[J].IEEE Transactions on Power Electronics, 2010, 25(10): 2642–2652.DOI:10.1109/TPEL.2010.2050908

[11]	ZHU M, YU K, LUO F L. Switched inductor Z-source inverter[J].IEEE Transactions on Power Electronics, 2010, 25(8): 2150–2158.DOI:10.1109/TPEL.2010.2046676

[12]	NGUYEN M K, LIM Y C, CHO G B. Switched-inductor quasi-Z-source inverter[J].IEEE Transactions on Power Electronics, 2011, 26(11): 3183–3191.DOI:10.1109/TPEL.2011.2141153

[13]	邓凯, 梅军, 郑建勇, 等. 改进型开关电感准Z源逆变器[J].电网技术, 2013, 37(11): 3254–3261.DENG K, MEI J, ZHENG J Y, et al. Improved switched-inductor quasi-Z source inverter[J].Power System Technology, 2013, 37(11): 3254–3261.(in Chinese)

[14]	PENG F Z, SHEN M S, QIAN Z M. Maximum boost control of the Z-source inverter[J].IEEE Transactions on Power Electronics, 2005, 20(4): 833–838.DOI:10.1109/TPEL.2005.850927

[15]	蔡春伟, 曲延滨, 盛况. 增强型Z 源逆变器[J].中国电机工程学报, 2011, 31(S1): 259–266.CAI C W, QU Y B, SHENG K. Enhanced Z-source inverters[J].Proceedings of the Chinese Society for Electrical Engineering, 2011, 31(S1): 259–266.(in Chinese)

[16]	GAJANAYAKE C J, VILATHGAMUWA D M, POH C L, et al. Z-source-inverter-based flexible distributed generation system solution for grid power quality improvement[J].IEEE Transactions on Energy Conversion, 2009, 24(3): 695–704.DOI:10.1109/TEC.2009.2025318

[17]	LIU Y S, GE B M, ABU-RUB H, et al. An effective control method for quasi-Z-source cascade multilevel inverter-based grid-tie single-phase photovoltaic power system[J].IEEE Transactions on Industrial Information, 2014, 10(1): 399–407.DOI:10.1109/TII.2013.2280083

[18]	杨水涛, 丁新平, 张帆, 等. Z-源逆变器在光伏发电系统中的应用[J].中国电机工程学报, 2008, 28(17): 112–118.YANG S T, DING X P, ZHANG F, et al. Study on Z-source inverter for photovoltaic generation system[J].Proceedings of the Chinese Society for Electrical Engineering, 2008, 28(17): 112–118.(in Chinese)

[19]	许颇, 张兴, 张崇巍, 等. 采用Z源变换器的小型风力并网逆变系统[J].电工技术学报, 2008, 23(4): 93–97.XU P, ZHANG X, ZHANG C W, et al. Small wind turbine grid-connected systems based on Z-source inverter[J].Transactions of China Electrotechnical Society, 2008, 23(4): 93–97.(in Chinese)