由于军事敏感性,关于有源对消研究的可见文献较少。其中文献[3],其从原理上分析对消波的频率、幅度与相位的要求,并定量地给出了频率、初相位与幅度误差对对消效果的影响;文献[4]阐述了有源隐身的电磁学基础,并计算了相干对消的波瓣特性、功率指标及对消波的幅相取值条件;文献[5]采用数理统计的方法计算了有源隐身目标散射场和对消场差值的均值和均方差,在方位角上分别在均匀和随机规律情况下,对对消效果进行了统计分析;文献[6]阐述了有源隐身技术的分类及其实现途径,并创造性地提出了相控阵法实现对消式有源隐身的技术方案,并提出了对消度这一衡量对消效果的参数;文献[7]基于目标的雷达散射截面(RCS)特性,具体分析了满足有源对消隐身条件下的幅值和相位误差对隐身效果的影响,并对关键技术进行了讨论;文献[8]提出了一种基于雷达相控阵技术,结合数字射频存储器和现场可编程门阵列的转发式有源对消隐身系统方案,并基于信号的群延迟特性,提出了一种针对线性调频和非线性调频信号的对消系统;文献[9]提出了一种新的回波对消算法,即将线性调频(LFM)信号与其自身延迟信号相乘,获得延迟与频率之间的线性关系并对其进行移频然后进行幅度和相位调制,实现与目标回波对消的作用;文献[10]以信号的间歇采样转发为切入点,从干扰信号经匹配滤波后的输出信号角度,提出了一种通过转发时延、频率、功率等参数的调制来实现干扰信号与目标信号的反相对消;文献[11]则更具体地细化了相关技术细节,并指出了参数的不同调制对对消效果的影响。上述文献或是仅从理论上阐述了技术途径,或是提出的方案均需要预先建立目标的全向散射特性数据库,而后根据对消装置探测到的对方雷达信号后调取相应信号下目标的散射特性信号数据,而后调制产生对应的对消信号发射对消波与目标的散射回波相对消,而目标的散射特性是极其复杂的函数,由此会产生一系列的累计误差以及调取庞大的数据库会存在更大的时延问题,从而导致结果可信度降低且工程实验难度较大。
本文在前人研究的基础上,以平面波与柱面波的相干对消效果为前提,提出了一种基于LFM波的转发干扰式有源对消系统,该系统由对消装置探测到对方雷达信号后经过一系列的调制产生对消波,与对方的来波信号直接相对消,避免了建立目标全向散射特性数据库以及系统提取数据库数据的时延等累计误差,时延更少、误差更小,步骤简单易实现,具有较高可信度与可实现度,为工程实现提供了参考。
1 有源对消的电磁学原理 雷达散射截面是目标散射特征的重要参数,其表达式为
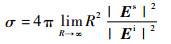 | (1) |
式中:Es和Ei分别为反射到雷达的反射电场矢量和入射电场矢量;R为探测雷达与目标之间的距离。因此,通过有源手段使得目标回波被抵消减弱,从而降低目标的雷达散射截面,实现隐身目的,即为有源对消隐身。
本文所提出的对消系统,采用对来波采样并转发,通过合理的间歇采样干扰参数选择,可以使产生的低阶假目标相位与真实目标相反、幅值相近、时域重叠,从而使其在对方雷达天线端的匹配滤波输出与原入射波回波的匹配输出进行相干抵消,降低目标的可检测性。其流程图如图 1所示。
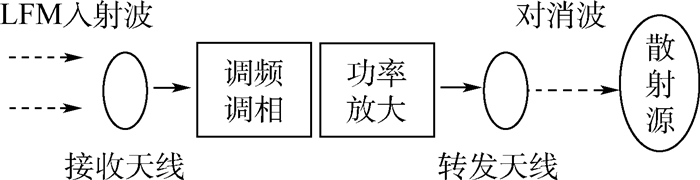 |
| 图 1 LFM波的有源对消隐身技术方案 Fig. 1 System of active cancellation stealth technology based on LFM wave |
| 图选项 |
2 平面波与柱面波的相干抵消效果 由于对消系统接收到对方探测信号后发出的对消信号是以球面波或柱面波的形式发出,而对方来波信号一般是平面波的形式,因此需要先验证柱面波与平面波的对消效果。另一方面,对方来波的方向是随机的,与系统所发射的对消波的传播方向可能不在一条直线上,从而有不同的夹角,因而要验证平面波与柱面波在不同夹角情况下的对消效果,以确定在不同角域内的不同对消效果,以便于做下一步的研究。下文将以柱面波为例,进行验证。
如图 2所示,设无限长理想导电圆柱半径为a,其轴线沿z轴放置,设入射波为波长为λ的平面波,其表达式为
 | (2) |
则其远区散射场[12]为
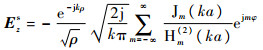 | (3) |
式中:k为真空中的波数;ρ为观察点到圆柱中心的距离;Jm(ka)为第一类m阶贝塞尔函数;Hm(2)(ka)为第二类m阶Hankel函数;φ为散射点(观察点)的相位。
对消波为柱面波,其相当于强度为Iz(ρ′)的无限长线电流,位于(ρ′,φ′)处,流向为z方向,则其散射场可以表示为
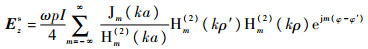 | (4) |
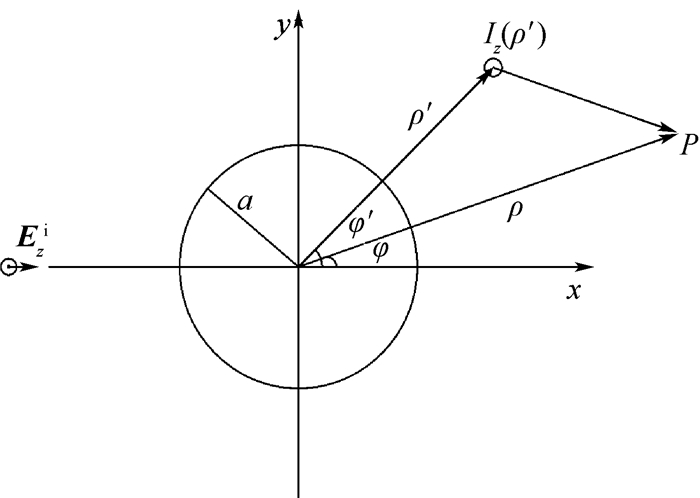 |
| 图 2 理想导电圆柱对平面波、柱面波的散射 Fig. 2 Scatter of plane wave and cylindrical wave by ideal conducting cylinder |
| 图选项 |
式中:ω为角频率;p为真空中磁导率;I为线电流的电流强度。
当ρ′=10λ,a=λ时,分别研究当对消柱面波与平面波的夹角为0°、30°、45°、60°、75°、90°时的对消效果,其仿真结果如图 3所示。
 |
| 图 3 平面波与柱面波不同夹角时的对消效果 Fig. 3 Cancellation effect at different angles between plane wave and cylindrical wave |
| 图选项 |
分析以上仿真结果可知,柱面波的散射场随着参数φ′的变化而左右移动。在φ′=180°附近时,目标后向(即φ=180°附近)合成场减弱区域明显增大;在φ′=180°亦即对消波与入射波夹角为0°时,柱面波的散射场形状与入射平面波的散射场基本一致,目标全向合成场均减弱,未有增强,对消效果较为明显,从而视为最佳对消。
由此可得结论,柱面波与平面波在满足一定条件下,是可以进行相干抵消的,从而为以下的有源对消系统提供了理论上的支持。
3 LFM信号的群延迟及对消波匹配滤波输出分析 3.1 接收信号及其匹配滤波器的群延迟特性 设接收信号为x(t),则其匹配滤波器的冲击响应为[13-16]
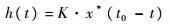 | (5) |
式中:K为常数;t为时间。则由此得信号的匹配滤波器频率响应为
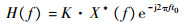 | (6) |
式中:X(f)为信号x(t)经匹配滤波器的傅里叶变换。
综上可得其相频特性函数为
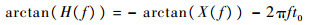 | (7) |
式中:arctan(H(f))为相位谱。
由此得到匹配滤波器的群延迟为
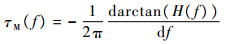 | (8) |
将式(7)代入式(8)中可得
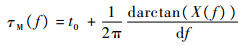 | (9) |
相应的,信号x(t)的群延迟为
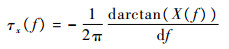 | (10) |
以上分析可知,匹配滤波器的群延迟特性正好和接收信号相反,则如果改变输入信号的群延迟特性的同时保持滤波器不变,将会使得信号经匹配滤波后的输出峰值点前移或滞后。
3.2 接LFM信号的频率调制特性 假设LFM信号为
 | (11) |
式中:τ为信号的脉宽;μ为调频斜率且μ=B/τ,B为信号带宽,当BT>>1时,信号的频谱为
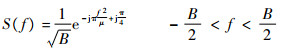 | (12) |
由式(12)和式(6)可得到信号s(t)的匹配滤波频率响应为
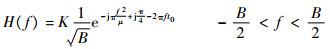 | (13) |
在进行频率调制时,若在原信号基础上进行fJ>0的频率调制,则可得到干扰的频谱为
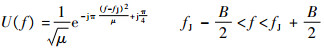 | (14) |
由以上分析可知,式(13)和式(14)在整个频率范围内的图形如图 4所示。
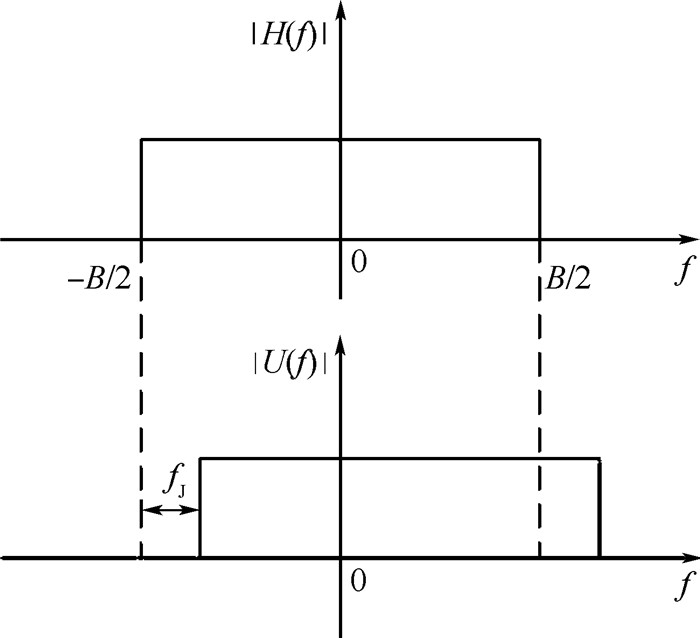 |
| 图 4 匹配滤波器频谱与对消波频谱的关系 Fig. 4 Relationship between spectrum of matched filter and spectrum of cancellation wave |
| 图选项 |
由图 4可知,在(-B/2,-B/2+fJ)区间内,只有原信号s(t)的输出;在(-B/2+fJ,B/2)内有原信号及干扰信号的输出;在(B/2,B/2+fJ) 区间内,只有干扰信号的输出。
3.3 对消波的匹配滤波输出分析 以LFM信号为例,设入射波信号为
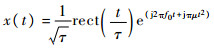 | (15) |
式中:f0为中心频率,其余各量与3.2节中定义相同。设对消系统的总延时为Δτ,并且对入射波信号分别进行Δφ、fm的相位和频率的调制,则转发对消波信号为
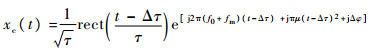 | (16) |
入射信号与对消信号经目标反射后共同进入接收机的匹配滤波器,可表示成接收信号的形式为
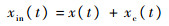 | (17) |
则经匹配滤波后的输出信号为
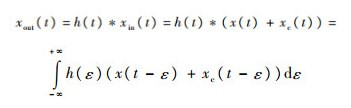 | (18) |
式中:h(t)为接收机匹配滤波器的冲击响应且
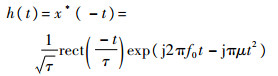 |
综合以上信息,对式(18)进行积分可得最终匹配滤波输出信号xout(t)的表达式为
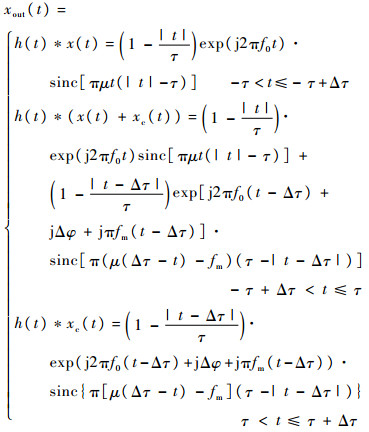 | (19) |
式(19)表明,经调频、调相后的匹配滤波输出分为3段:第1段为(-τ,Δτ-τ],只有入射波信号x(t)产生输出;第2段为(Δτ-τ,τ]入射波与对消波均产生输出;第3段为(τ,Δτ+τ],只有对消波产生输出。各段输出包络均为sinc函数。此结果与3.2节所分析的结果一致,印证了分析的正确性。
由于对消装置时延Δτ相对于τ很小,因此第1段和第3段的峰值均较小;第2段分为入射波和对消波两部分的匹配滤波输出之和,前者在t=0时取峰值1,后者在因子μ(Δτ-t)-fm=0亦即t=Δτ-fm/μ时取得峰值1-fm/(μτ),此时两者相位差为Δφ=jΔφ+jπfm(t-Δτ)-j2πf0Δτ。由对消方案知须使得两者的峰值出现在同一时刻且相位相反,则可得
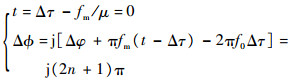 | (20) |
式中:n为整数,解之得
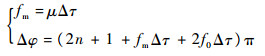 | (21) |
由此可知,通过控制参数fm、Δφ达到式(21)的要求,可使入射波的回波输出与对消波的回波输出峰值出现在同一时刻、相位相差(2n+1)π,从而使得对消后信号的输出峰值为
 |
但是此时需要事先知晓或是探测出对方雷达信号的f0、μ等参数,以及对自身对消装置系统的时延的控制。
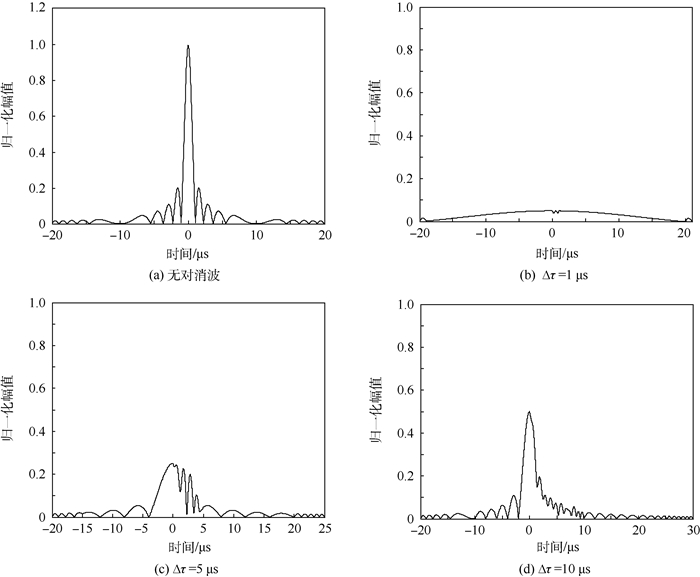
4 仿真验证 设入射波信号参数为:f0=1.2 GHz、B=5 MHz、τ=20 μs,利用MATLAB进行仿真编程可直观呈现上述分析的仿真结果。由3.3节的分析可知,对消后输出信号的峰值由Δτ/τ的值决定,图 5给出了B=5 MHz、无对消信号以及Δτ分别为1、5、10 μs时对消后信号输出情况(由于不同目标的散射特性不尽相同,从具有统一性和便于理解、直观地表现出对消前后信号的变化程度的角度来说,此处用归一化幅值)。
 |
| 图 5 不同时延的对消效果(B=5 MHz) Fig. 5 Cancellation effect at different time-delay(B=5 MHz) |
| 图选项 |
分析以上仿真结果可知,对消后输出波的峰值与Δτ/τ比值呈正相关,即当控制时延在很小的数量级时,对消效果则更加明显。
另外,带宽对对消效果亦有一定的影响。可令带宽B=1 MHz,其余参数不变,进行仿真结果如图 6所示。
对比图 5与图 6可知,带宽B对对消后信号的峰值没有影响,其影响信号主峰的宽窄,带宽越大,主峰越窄,从探测的角度来讲,越有利于飞行器的隐身。
 |
| 图 6 不同时延的对消效果(B=1 MHz) Fig. 6 Cancellation effect at different time-delay(B=1 MHz) |
| 图选项 |
5 结 论 1) 本文提出的基于LFM波的有源对消隐身技术方案,适用的平台为大中型飞行器,这样使得对消波的波形更加接近于平面波的形式,否则会出现误差较大的情况。
2) 验证了以无限长理想导电圆柱为散射源的情况下,平面波与柱面波的对消效果;不同观察视角、对消波与入射波的夹角都会对对消后散射场的幅值产生较大影响;在对消波与入射波夹角为0°时,每一观察视角处都有隐身效果,没有出现信号增强的情况。
3) 分析并仿真了所提对消系统的对消效果。进行调频、调相后的对消波与入射波的对消很大程度上取决于时延的大小,且对消后信号输出的峰值与Δτ/τ有直接的关系;带宽对于信号主峰的宽窄有直接的影响,带宽越大,则主峰越窄。
参考文献
| [1] | 贺媛媛, 周超. 飞行器隐身技术研究及发展[J].飞航导弹, 2012(1): 84–91.HE Y Y, ZHOU C. The research and development of the aircraft stealth technology[J].Aerodynamic Missile Journal, 2012(1): 84–91.(in Chinese) |
| [2] | 向迎春, 曲长文, 李柄荣, 等. 基于舰船雷达散射特性的对消隐身仿真研究[J].系统仿真学报, 2013, 25(1): 104–110.XIANG Y C, QU C W, LI B R, et al. Simulation research on cancellation stealth of warship based on its radar scattering properties[J].Journal of System Simulation, 2013, 25(1): 104–110.(in Chinese) |
| [3] | 洪光启, 陈图强, 吴晓葆. 雷达有源对消原理研究[J].雷达与对抗, 1995(1): 32–35.HONG G Q, CHEN T Q, WU X B. The principle research on radar active cancellation stealth[J].Radar & ECM, 1995(1): 32–35.(in Chinese) |
| [4] | 邓扬建, 张杰儒. 雷达有源隐身技术研究[J].电子对抗技术, 1997(4): 11–17.DENG Y J, ZHANG J R. The research on radar active cancellation stealth technology[J].Electronic Information Warfare Technology, 1997(4): 11–17.(in Chinese) |
| [5] | 杨小鹏, 赵维江, 黄立伟. 目标RCS的计算和对消效果的统计分析[J].电波科学学报, 2002, 17(1): 88–92.YANG X P, ZHAO W J, HUANG L W. Calculation of RCS of targets and statistical analysis of cancellation effect[J].Chinese Journal of Radio Science, 2002, 17(1): 88–92.(in Chinese) |
| [6] | 梁百川. 有源隐身技术研究[J].舰船电子对抗, 2004, 27(1): 3–6.LIANG B C. Study on active stealth techniques[J].Shipboard Electronic Countermeasure, 2004, 27(1): 3–6.(in Chinese) |
| [7] | 曲长文, 向迎春. 基于目标RCS特性的有源对消隐身分析[J].雷达科学与技术, 2010, 8(2): 109–112.QU C W, XIANG Y C. Active cancellation stealth analysis based on RCS characteristic of target[J].Radar Science and Technology, 2010, 8(2): 109–112.(in Chinese) |
| [8] | 徐胜.雷达有源对消隐身技术研究[D].北京:北京航空航天大学,2013:11-92.XU S.Research on radar active cancellation stealth technique[D].Beijing:Beihang University,2013:11-92(in Chinese). |
| [9] | 王玉军, 赵国庆, 王宏伟. 一种LFM雷达回波对消干扰算法[J].西安电子科技大学学报, 2008, 35(6): 1031–1035.WANG Y J, ZHAO G Q, WANG H W. Echo cancelling algorithm for the LFM radar[J].Journal of Xidian University, 2008, 35(6): 1031–1035.(in Chinese) |
| [10] | 冯德军, 王伟, 徐乐涛. 对V-调频信号的间歇采样转发干扰研究[J].雷达科学与技术, 2013, 11(2): 209–213.FENG D J, WANG W, XU L T. Jamming V-FM signal using interrupted-sampling repeater[J].Radar Science and Technology, 2013, 11(2): 209–213.(in Chinese) |
| [11] | 陈世春, 黄沛霖, 姬金祖. 线性调频波的转发干扰对消分析[J].北京航空航天大学学报, 2014, 40(7): 939–946.CHEN S C, HUANG P L, JI J Z. Analysis on repeater jamming active cancellation for linear frequency modulated wave[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(7): 939–946.(in Chinese) |
| [12] | 杨儒贵. 高等电磁理论[M].北京: 高等教育出版社, 2008: 224-239.YANG R G. Advanced electromagnetic theory[M].Beijing: Higher Education Press, 2008: 224-239.(in Chinese) |
| [13] | 王雪松, 刘建成, 张文明, 等. 间歇采样转发干扰的数学原理[J].中国科学(E辑:信息科学), 2006, 36(8): 891–901.WANG X S, LIU J C, ZHANG W M, et al. The mathematical principle of interrupted-sampling repeater[J].Science in China (Series E:Information Sciences), 2006, 36(8): 891–901.(in Chinese) |
| [14] | 刘建成, 刘忠, 王雪松, 等. 基于群延迟的前移干扰研究[J].自然科学进展, 2007, 17(1): 99–105.LIU J C, LIU Z, WANG X S, et al. Study on the group delay based on forward jamming[J].Progress in Natural Science, 2007, 17(1): 99–105.(in Chinese) |
| [15] | 冯德军, 徐乐涛, 王雪松. 间歇采样转发假目标的相位特性及其在角度欺骗干扰中的应用[J].国防科技大学学报, 2014, 36(3): 135–140.FENG D J, XU L T, WANG X S. Phase signature of active decoy and its application in angular deception jamming using interrupted-sampling repeater[J].Journal of National University of Defense Technology, 2014, 36(3): 135–140.(in Chinese) |
| [16] | XU S, XU Y M. Assemble an active cancellation stealth system[J].Microwaves & RF, 2012, 51(7): S16–S21. |
