1 量子万有引力搜索算法 QGSA是由Soleimanpour-Moghadam等[8]在GSA的基础上提出的一种新型的智能算法。GSA是基于牛顿万有引力的一种元启发式算法[9-10],其凭借个体之间的万有引力作用实现优化信息的共享,引导粒子群在最优解的范围内进行搜索。在GSA中,粒子的状态是由其位置和速度决定的。但是在量子力学的理论中,粒子的状态由波函数 ψ 决定。
在量子力学中,薛定谔方程是求解粒子状态问题的基本方程。沿r轴运动的粒子的薛定谔方程表达式为
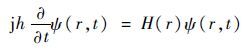 | (1) |
式中:H为哈密顿算子,表示波函数的总能量;h为普朗克常量。
哈密顿函数表示为
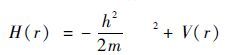 | (2) |
式中:m为粒子的质量;V(r)为势阱分布函数。
在薛定谔方程中,波函数 ψ 没有直接的物理定义。然而,|ψ|2为粒子运动的概率密度,能够计算出粒子在特定时间出现在某一位置上的概率。在三维空间中,粒子的波函数为ψ(r,t),可表示为
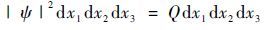 | (3) |
式中: Qdx1dx2dx3 表示t时刻,在点(x1,x2,x3)周围大量的元素中寻找出粒子位置的测量概率。
因此,概率密度函数|ψ|2应满足:
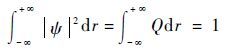 | (4) |
假设存在一个一维空间的粒子,则这个粒子在一维δ势阱中的势能可以表示为
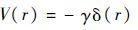 | (5) |
式中: γ 为与势阱深度相关的正比例变量,势阱深度是原点处无穷大、其余位置处为0的函数; δ(r) 为狄拉克函数。
综上所述,薛定谔方程可以表示为
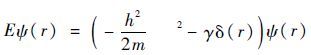 | (6) |
式中:E为粒子本身的能量。
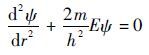 | (7) |
为防止粒子越界,给出如下限定条件:
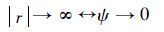 | (8) |
为了满足上述条件,式(7)可表示为
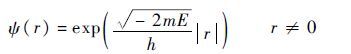 | (9) |
精确的粒子位置信息是确定适应度值的必要条件。但是,量子波动函数只能给出粒子位于空间不同位置的概率密度函数。因此,获得粒子位置成为解决问题的先决条件。根据蒙特卡罗方法使用随机数来解决计算问题的理念,可将式(9)作如下简化:
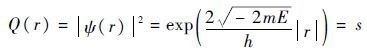 | (10) |
式中:s为[0,1]范围内服从正态分布的随机数。
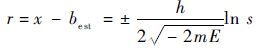 | (11) |
式中:x为粒子的位置;best为由拥有最好适应度值的K个粒子决定的粒子信息,K为时间函数,随着时间t的增加,K从 K0 逐渐减小到1,即最后只有最优的一个粒子起作用。
如此便可以得到粒子位置的表达式为
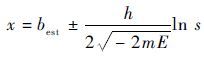 | (12) |
综上所述,QGSA的迭代过程总结如下:
1) 初始化粒子的位置。在D维搜索空间内随机生成N个粒子,其中粒子的位置可表示为
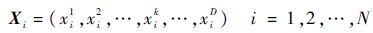 |
2) 分别计算N个粒子的适应度值。
3) 选择群体中的U和V。设在t时刻,只允许拥有最好适应度值的K个粒子对其他粒子起作用。U为K个粒子中拥有最优适应度值的粒子的位置,V为单个粒子在迭代过程中适应度值最优时的粒子位置。每次迭代后,若当前粒子适应度值最优,则使用当前粒子位置替换V[11]。
4) 更新Gi。更新公式如下:
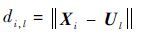 | (13) |
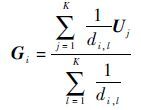 | (14) |
式中:di,l为粒子i与粒子l之间的欧氏距离;G为粒子的惯性质量。
5) 更新每个粒子的位置Pi。通过式(15)更新粒子的位置:
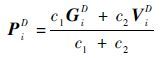 | (15) |
式中: c1 和 c2 为在[0,1]范围内的随机数。
运用蒙特卡罗方法,得粒子移动迭代公式为
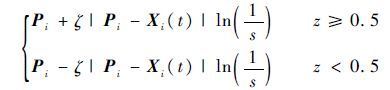 | (16) |
式中:ζ为收缩膨胀的系数,用随机数表示;z为[0,1]范围内的随机数。
6) 迭代操作。判断是否达到最优位置或达到最大迭代次数。是,则退出;否,则回到步骤2)继续执行。
2 支持向量机 SVM是由Vapnik和Cortes[12]提出的一种基于结构风险最小化的机器学习技术,其能够逼近任意复杂的非线性系统,依据较少样本信息在模型复杂性和学习能力之间寻求最优,以获得最好的泛化能力。
对于2类线性可分样本集,SVM实质上是在寻找一个分类超平面,使得2类样本能够分布在超平面的两边,且距离超平面最远[13]。
设有2类数据样本为
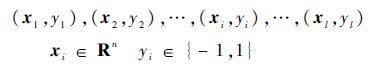 |
式中:n为样本空间的维数;l为训练样本的总数; xi 为第i个样本空间输入值; yi 为第i个输出值。
对于线性可分的情况,最优超平面的求解可以归结为如下约束优化问题:
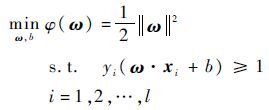 | (17) |
式中: φ(ω) 为最优超平面;ω为最优超平面的法向量;b为偏移值。
ω·x+b=0 就是所要寻找的最优超平面。
当样本线性不可分时,SVM采用非线性映射 Φ 将数据样本从现属空间映射到高维空间 Ω ,再在 Ω 中求最优分类面。SVM运用核函数巧妙地解决了高维空间维数过高的问题,该核函数 K(xi,xj) 满足Mercer条件,其对应于变换空间的内积,即 K(xi,xj)=Φ(xi)·Φ(xj) ,内积运算在未知 Φ(x) 具体形式的情况下即可实现[14]。综上所述,通过选择适当的核函数 K(xi,xj) ,便可以实现非线性样本的线性分类。同时引入松弛变量 ξi 后,原分类面方程可表示为
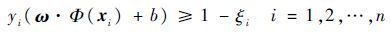 | (18) |
综上所述,构造最优分类面的问题转化为
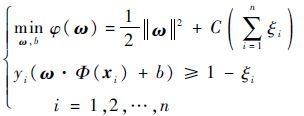 | (19) |
式中:常数C为惩罚因子,控制模型的复杂度以及逼近误差。
通过引入Lagrange乘法算子α,把构建最优超平面的问题转化为对偶二次规划问题(见式(20))[15],同时将核函数的内积转换代入,式(19)转换为
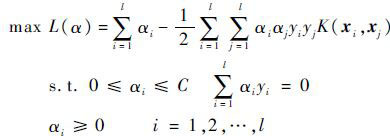 | (20) |
最终的最优分类面函数表示为
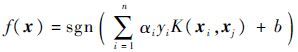 | (21) |
同时,不同的核函数对应着不同的SVM分类器。目前,SVM中应用效果较好的核函数主要有线性核函数、径向基核函数、多项式核函数和sigmoid函数等[16],本文主要选择径向基核函数作为SVM的核函数。径向基核函数定义如下:
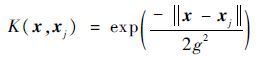 | (22) |
式中:g为径向基核函数的核宽度。
SVM的参数选取对于其学习能力以及推广能力均有较大的影响,对于径向基核函数的SVM而言,需要确定的参数主要包括惩罚因子C和核宽度g。本文采用QGSA对C和g寻优,从而得出分类模型最优的C和g。
3 基于量子万有引力搜索算法的支持向量机 基于QGSA的SVM以SVM分类模型框架为基础,采用基于QGSA智能算法的粒子更新策略。其中,以粒子位置信息表示SVM的一种参数组合,通过QGSA位置更新策略,获得最优粒子位置,代入SVM建立最优SVM分类模型。
基于QGSA的SVM故障诊断模型建立的具体步骤如下:
1) 将仿真获得的样本数据随机分为训练集样本和测试集样本。
2) 随机产生n个粒子,每一个粒子位置代表一组参数(C,g)。
3) 根据SVM参数C和g的特征确定其取值范围以及更新步长,以此来决定QGSA中的粒子位置的迭代范围以及更新步长。
4) 每次迭代过程中,将每个粒子位置代入SVM故障诊断模型中,得出当前粒子的适应度值。
5) 以适应度值为依据,V代表每个粒子目前为止的最优位置,U代表全局粒子的最优位置。每次迭代后,若当前粒子位置优于V,则使用当前位置替换V;否则,不替换,并将目前位置最优的粒子位置存入U。
6) 根据QGSA的位置更新策略更新粒子位置,并判断是否满足要求。如果满足要求,则停止搜索;否则,返回步骤3)继续寻优。
7) 以获得的最优参数为基础建立故障诊断模型,进行故障诊断。
QGSA优化SVM参数流程如图 1所示。
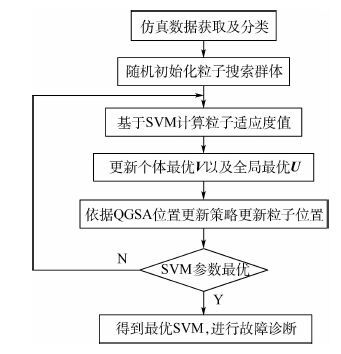 |
| 图 1 QGSA优化SVM参数流程 Fig. 1 Flowchart of SVM parameters optimization by QGSA |
| 图选项 |
4 结果分析 根据自动驾驶仪的工作原理以及电路结构,本文通过电路仿真的手段仿真自动驾驶仪电路模型,并模拟自动驾驶仪的典型故障进行故障样本集的采集。9类故障的正常值与故障值对比见表 1。仿真电路故障包括无故障类(NF)、R3↑、R3↓、R8↑、R8↓、R16↑、R16↓、C1↑和C1↓。其中,↑或↓表示故障值相对于正常值向上或向下偏离。按照表 1中9种故障共整理出540组数据,将样本数据分为训练集和测试集,作为验证模型的依据。
表 1 9类故障的正常值与故障值对比 Table 1 Comparison of normal and fault values among 9 types of faults
| 故障ID | 故障 | 正常值 | 故障值 |
| F0 | NF | ||
| F1 | R3↑ | 10kΩ | 16kΩ |
| F2 | R3↓ | 10kΩ | 4kΩ |
| F3 | R8↑ | 280kΩ | 430kΩ |
| F4 | R8↓ | 280kΩ | 130kΩ |
| F5 | R16↑ | 150kΩ | 230kΩ |
| F6 | R16↓ | 150kΩ | 70kΩ |
| F7 | C1↑ | 1.8μF | 3μF |
| F8 | C1↓ | 1.8μF | 0.8μF |
表选项
将训练集样本数设置为50时,基于遗传算法的SVM、基于GSA的SVM以及基于QGSA的SVM的故障诊断结果如图 2所示。
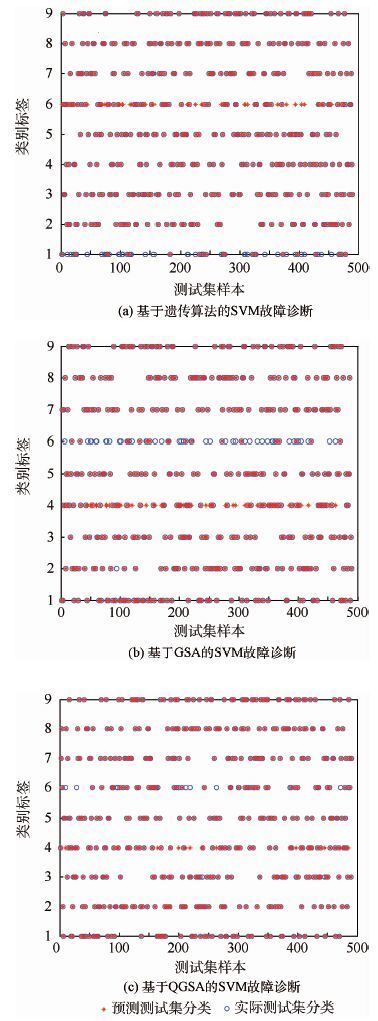 |
| 图 2 基于遗传算法的SVM、基于GSA的SVM和基于QGSA的SVM的故障诊断分类准确率 Fig. 2 Accuracy of GA-SVM,GSA-SVM and QGSA-SVM fault diagnosis |
| 图选项 |
由3种故障诊断的分类准确率可以看出,基于QGSA的SVM故障诊断的分类准确率明显高于其余2种。为进一步验证基于QGSA的SVM故障诊断在不同样本数下的表现,设置不同样本数,依次验证3种故障诊断模型的诊断效果,诊断结果见表 2。可知,基于QGSA的SVM故障诊断模型在样本数为70的情况下,分类准确率已达99.1489%,能够在小样本故障诊断中保持较高的分类准确率。
表 2 3种故障诊断模型分类准确率对比 Table 2 Comparison of accuracy among three fault diagnosis models
| % | |||
| 训练集样本数 | 基于遗传算法的SVM | 基于GSA的SVM | 基于QGSA的SVM |
| 10 | 37.7358 | 26.9811 | 54.7170 |
| 20 | 51.5384 | 49.6154 | 88.4615 |
| 30 | 88.4313 | 80.0000 | 93.1373 |
| 40 | 90.4000 | 79.4000 | 95.8000 |
| 50 | 92.0408 | 91.6327 | 96.5306 |
| 60 | 96.2500 | 93.5417 | 97.2917 |
| 70 | 98.9362 | 97.8723 | 99.1489 |
表选项
5 结 论 本文针对自动驾驶仪故障样本较少的问题,提出基于QGSA优化的SVM自动驾驶仪故障诊断模型。
1) 算法可在故障样本较少的情况下,得到较高的故障诊断分类准确率。例如在故障样本数为20时,故障的分类准确率便能够达到88.4615%。
2) 算法在相同的样本数下,相比于基于GSA的SVM和基于遗传算法的SVM,具有更高的故障诊断分类准确率。
为使本文提出的方法能够处理各种类型的故障诊断模型,仍需要优化方法的各项参数,进一步提高方法的收敛速度以及诊断准确率。
参考文献
| [1] | 钟宇, 白云, 黄孝文. 基于RBF神经网络的导弹自动驾驶仪故障诊断[J]. 现代防御技术,2011, 39(2): 54–59.ZHONG Y, BAI Y, HUANG X W. Fault diagnosis of missile autopilot based on RBF neural network[J]. Modern Defence Technology,2011, 39(2): 54–59.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [2] | 刘东平, 单甘霖, 张岐龙, 等. 基于改进遗传算法的支持向量机参数优化[J]. 微计算机应用,2010, 31(5): 11–15.LIU D P, SHAN G L, ZHANG Q L, et al. Parameters optimization of support vector machine based on improved genetic algorithm[J]. Microcomputer Applications,2010, 31(5): 11–15.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [3] | ALWAN H B,KU-MAHAMUD K R.Optimizing support vector machine parameters using continuous ant colony optimization[C]//20127th International Conference on Computing and Convergence Technology.Piscataway,NJ:IEEE Press,2012:164-169. |
| Click to display the text | |
| [4] | 宋晓华, 杨尚东, 刘达. 基于蛙跳算法的改进支持向量机预测方法及应用[J]. 中南大学学报(自然科学版),2011, 42(9): 2737–2740.SONG X H, YANG S D, LIU D. Improved support vector machine forecasting model by shuffled frog leaping algoritmh and its application[J]. Journal of Central South University (Science and Technology),2011, 42(9): 2737–2740.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | 薛浩然, 张珂珩, 李斌, 等. 基于布谷鸟算法和支持向量机的变压器故障诊断[J]. 电力系统保护与控制,2015, 43(8): 8–13.XUE H R, ZHANG K H, LI B, et al. Fault diagnosis of transformer based on the cuckoo search and support vector machine[J]. Power System Protection and Control,2015, 43(8): 8–13.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [6] | ZHANG W, NIU P, LI G, et al. Forecasting of turbine heat rate with online least squares support vector machine based on gravitational search algorithm[J]. Knowledge-Based Systems,2013, 39(2): 34–44. |
| Click to display the text | |
| [7] | 戢钢, 王景成, 葛阳, 等. 城市小时级需水量的改进型引力搜索算法-最小二乘支持向量机模型预测[J]. 控制理论与应用,2014, 31(10): 1376–1382.JI G, WANG J C, GE Y, et al. Gravitational search algorithm-least squares support vector machine model forecasting on hourly urban water demand[J]. Control Theory and Applications,2014, 31(10): 1376–1382.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [8] | SOLEIMANPOUR-MOGHADAM M, NEZAMABADI-POUR H, FARSANGI M M. A quantum inspired gravitational search algorithm for numerical function optimization[J]. Information Sciences,2014, 267(5): 83–100. |
| Click to display the text | |
| [9] | RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S. GSA:A gravitational search algorithm[J]. Information Sciences,2009, 179(13): 2232–2248. |
| Click to display the text | |
| [10] | RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S. BGSA:Binary gravitational search algorithm[J]. Natural Computing,2010, 9(3): 727–745. |
| Click to display the text | |
| [11] | SOLEIMANPOUR-MOGHADAM M, NEZAMABADI-POUR H, FARSANGI M M. A quantum behaved gravitational search algorithm[J]. Intelligent Information Management,2012, 4(6): 390–395. |
| Click to display the text | |
| [12] | CORTES C, VAPNIK V. Support-vector networks[J]. Machine Learning,1995, 20(3): 273–297. |
| Click to display the text | |
| [13] | DONG S, LUO T. Bearing degradation process prediction based on the PCA and optimized LS-SVM model[J]. Measurement,2013, 46(9): 3143–3152. |
| Click to display the text | |
| [14] | 张周锁, 李凌均, 何正嘉. 基于支持向量机的机械故障诊断方法研究[J]. 西安交通大学学报,2002, 36(12): 1303–1306.ZHANG Z S, LI L J, HE Z J. Research on diagnosis method of machinery fault based on support vector machine[J]. Journal of Xi'an Jiaotong University,2002, 36(12): 1303–1306.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [15] | 李琼, 陈利. 一种改进的支持向量机文本分类方法[J]. 计算机技术与发展,2015, 25(5): 78–82.LI Q, CHEN L. An improved support vector machine text classification method[J]. Computer Technology and Development,2015, 25(5): 78–82.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [16] | 庄严, 白振林, 许云峰. 基于蚁群算法的支持向量机参数选择方法研究[J]. 计算机仿真,2011, 28(5): 216–219.ZHUANG Y, BAI Z L, XU Y F. Research on parameters of support vector machine based on ant colony algorithm[J]. Computer Simulation,2011, 28(5): 216–219.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
