传感器配置主要有2个任务:①选择合适的传感器组合,在系统各项约束的前提下满足系统各项性能指标要求,这种系统性能指标定义为系统性能优值(FOM),一般包括系统可观测性能、故障检测性能、故障隔离性能和传感器成本等;②优化传感器布局,通常在配置传感器过程中,系统的诊断段性能或故障观测性能是一个NP(Non-deterministic Polynomial)完全问题,即多项式复杂程度的非确定性问题,它的计算困难程度随着求解变量数量的增加而增加,穷举算法最先被用于优化布局问题,算法对每一种可能的布局评估,从而找到一组最优布局,适用于传感器数量较少的机电系统传感器布局优化。
与故障诊断方法类似,传感器配置也可分定性和定量分析法两大类。定性的方法如有向图(SDG)法[3],用有向图建立传感器和故障之间的内在联系模型,确定故障的传播模式和对于传感器的影响,以此来确定覆盖所有故障节点的传感器组合。定量方法如使用解析冗余关系(ARR)构造系统模型方程,通过对ARR结构的分析来推导传感器的配置,无须推导所有系统残差,只需分析与传感器相关的残差,降低了计算量。然而如等价空间法及观测器法这类解析方法只能对于执行机构或传感器故障做出诊断,对于参数性故障(如电阻、电感故障)无法通过此类方法诊断。
键合图(BG)[4-5]可以用图形模式直接表示系统参数或测量过程的不确定性[6],使用覆盖的因果路径方法,利用它的结构形式生成解析冗余关系式,利用它基本图元的因果关系性质来消除系统未知变量,建立直接的故障特征矩阵以确定故障的起源。在无须先行推导系统方程的前提下,分析故障现象,得到的图形化模型,不仅可用于建模,也可用于诊断,进而解决传感器配置问题。文献[7]利用系统键合图模型的因果关系推导出差分代数方程(DAE),通过对所有加入故障的DAE矩阵的相空间分析,得到最佳的传感器布局。文献[8]对风力发电系统建立键合图模型,通过对几组假设传感器组合推导的残差式和故障特征矩阵的分析,得出所有故障可观测并可隔离。文献[9]提出一种基于诊断元件故障的键合图传感器布局方法,并将其用于一个两罐系统模型。
本文使用键合图作为系统建模以及传感器布局的工具,通过模型推导残差,在对残差、故障检测与隔离、传感器布局三者间的关系分析的基础上,提出一种新的传感器布局方法。
1 键合图建模方法 1.1 基本图元 键合图总结了多能域变量之间相似的物理性质,用相同图元来表示不同域理想元件。按图元与能量作用关系可将键合图图元划分为5大类,分别是能量供应与吸收元件Se、Sf(如电压、电流源)、储能元件C、I(如电容、电感元件)、耗能元件R(如电阻)、能量转换元件TF、GY(如变压器、电动机)、测量元件De、Df(如传感器),通过这5类基本图元构建键合图系统健康监测模型见图 1。
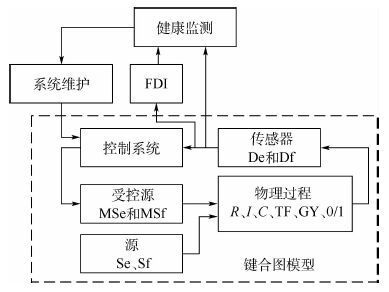 |
| 图 1 键合图系统健康监测模型 Fig. 1 Healthy monitoring system based on bond graph model |
| 图选项 |
1.2 同步电机建模基础 同步电机是一种能量转换设备,由定子和转子组成,转子绕组接入外部直流电产生励磁磁场,定子电枢三相绕组上流过三相交流电,两组线圈产生的气隙磁通变化使转子轴上的机械功率和定子绕组的电功率相互转化。
由于定转子间的相对运动,abc三相静止不动坐标系所建立的原始方程中会出现变系数,不便于建立模型。使用Park变换法,将原方程从 abc坐标系变为与转子相对静止的 dq 坐标系下,变换矩阵为
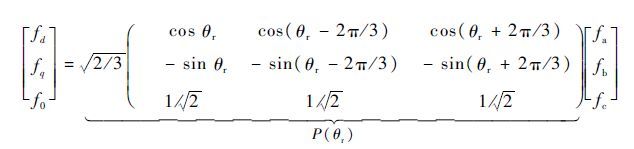 | (1) |
式中: fd 、 fq 和 f0 为dq坐标系下的物理量; fa 、 fb 和 fc 为abc坐标系下的物理量;P( θr )为 θr 的Park;d轴领先a轴转子角度
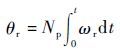
模型采用7阶方程描述同步发电机,其5阶
电磁方程的dq轴等效电路如图 2所示,图中:vds和vqs分别为定子在d轴上和q轴上的等效电压;ids和iqs分别为定子在d轴上和q轴上的等效电流;ψds和ψqs分别为定子在d轴上和q轴上的磁通;Rs和L1分别为定子等效电阻和漏电感;Lmd和Lmq分别为d轴上和q轴上的等效电流;RD和LD分别为阻尼绕组D等效电阻和电感;RQ和LQ分别为阻尼绕组Q等电阻和电感;vf、Rf和Lf分别为励磁电压、电阻和电感。各支路电流参考方向如图中标识。建模采用以下假设:①三相负载对称,忽略零轴分量;②忽略磁饱和、磁滞和涡流的影响;③电机的定子及转子具有光滑的表面,定转子的槽及通风沟等不影响定转子的电感。
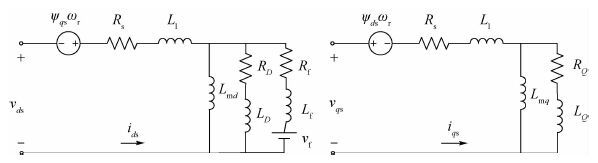 |
| 图 2 轴等效电路图 Fig. 2 Equivalent circuits of d-axis and q-axis |
| 图选项 |
2 基于键合图的传感器配置方法 2.1 残差与故障的关系 通过键合图模型的结构信息推导出的一组解析冗余关系ARR,即系统残差,它表示对于已知变量的动态/静态约束。对于各模式处于健康状态理想系统,系统各项残差应为零,然而由于系统模型方程线性化、模型降阶、外部扰动、测量噪声和未知参数等的影响,系统残差在一定的阈值范围内变化,若残差超过阈值则表示系统有故障发生。在系统监测过程中,残差可以作为故障指示器来诊断故障。
在实际系统中,对不同种类的故障,如快速变化的、对于系统危害度高的和缓慢变化的非致命性故障,需要采取不同的检测和诊断方法。对于前一种故障,可以采用状态估计和预测瞬时值与测量值的比较来诊断,而后一种故障则需要在系统一定时间的激励下采用如参数估计法来检测诊断[10]。本文所提出的传感器布置方法是针对快速高危害度的故障的检测。
由ARR生成的残差反映了系统变量 K 和约束 f 之间的关系,残差的一般表达式为
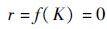 | (2) |
式中: K 为系统所有已知变量的集合,在键合图模型中, K 包含源变量MSf(e)、Sf(e)、传感器测量变量Df(e)、系统参数变量 θ(R,I,C) ,及输入信号 u 。
若需要得到残差 r ,需要消除系统未知中间变量,也就是连接各节点之间的键上的势e和流f变量。系统的结构信息、行为信息、测量信息和控制信息可用来消除这些中间变量:
1) 结构信息约束。通过键合图的节点能量关系推导节点能量守恒公式。如对于具有 n 个键的“0/1”节点的能量守恒方程为
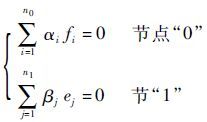 | (3) |
式中: ei 为与“1”节点连接的第 i 个键的势; fj 为与“0”节点连接的第 j 个键的流; αi,βj∈{-1,1} 为势与流的流入节点的方向; n0和n1 分别为与“0/1”节点相连的键的个数。
2) 行为信息约束。该类信息表达能量是如何通过元件转化的,在键合图中,用元件(R,C,I,TF,GY)的基本物理性质及公式作为约束条件。
3) 测量信息约束。表示传感器如何将状态变量转换为可用于FDI和控制的输出信号。
4) 控制信息约束。系统中有关控制变量和状态变量之间的约束关系。
结构故障特征矩阵(structural Fault Signature Matrix,FSM) DFSM 表示整个系统故障元件与残差的关系,如式(4)所示,矩阵元素 DFSMji 表示残差 ri 的变量集合 Ki 是否包含故障元件 θj 。
 | (4) |
假设系统有 n 个故障,故障集合为 F={f1,f2,…,fn} ,存在 m 个残差,残差集合为 R={r1,r2,…,rm} ,集合 XR 是一个残差子空间,若已知故障特征矩阵FSM,给出以下定义。
定义1 故障相关残差集合 AXi ,表示故障 fi 能够影响残差子空间 X 中的所有残差集合,用 AXi 表示该集合中残差的个数,当 AXi>0 时,表明故障 fi 与 X 是相关的,即故障 fi 是可检测的。
定义2 故障隔离残差集合 DXij ,表示能够分辨故障 fi 和故障 fj 所需要的残差集合,如式(5)所示, DXij 表示该集合中残差的个数,当 DXij>0 时,表明故障 fi 和故障 fj 是可隔离的。
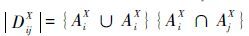 | (5) |
定义3 残差子空间故障指示度 ARRXiFDI ,其中 ρi 为故障的故障严酷度值, fi 为故障发生的概率, Fundect 为所有不可检测的故障集合, Funiso 为所有不可隔离的故障集合。式(6)为系统所有故障的检测性和隔离性在残差子空间 X 中的影响程度,该指数越小表示残差子空间 X 的故障检测性能越强,当所有故障均可检测和隔离时 ARRFDIX=0 。
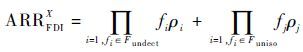 | (6) |
2.2 残差与传感器的关系 在理想情况下,残差对于不存在它结构中的故障不敏感,即若一个残差的表达式中不存在某个参数,那么这个参数的故障不会影响该残差,在这种情况下的ARR被称为结构性残差[11]。然而,如果故障数超过传感器的数量,或传感器布置不合理,那么就无法获得结构性ARR。结构性残差无法通过其他ARR代数推导得到,它的数量应该等于系统传感器的数量[12]。通过键合图模型推导的残差是代表了系统最小的解析冗余关系结构性残差。
本文采用传感器因果倒置的方法,按以下步骤对于布置了虚拟传感器的键合图推导残差:①对系统建立键合图模型,指定各元件的因果关系,首选微分因果关系以避免初始状态不确定问题;②选择一个源或传感器相连接的节点推导ARR,通过因果关系分析消除未知变量;③转移到下一个源和传感器相连接的节点推导ARR,若这个ARR的相关变量集合K与之前推导的ARR不同,则保留这个ARR,若相同则继续推导下一个节点;④重复步骤③直至所有与源和传感器相连接的节点推导完毕,所得到的一组ARR就是系统所有残差。
在默认因果关系的情况下,用因果路径法可以推导出未知变量 R、C、I 的势/流与传感器因果关系如式(7)~式(9)所示。
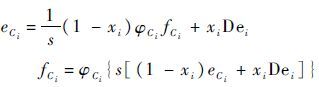 | (7) |
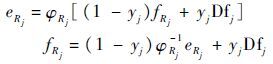 | (8) |
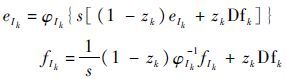 | (9) |
式中: 3个二元变量 xi、yj和zk 分别表示与元件 R、C和I 连接的“0/1”节点的传感器连接状态,当该节点有传感器连接时,相应变量值为1,否则为0;带下标的 e 和 f 分别为对应未知变量 R、C和I 上的势和流;s表示求导。
为了研究传感器配置问题,需要在键合图中相应的关键“0/1”节点处设立虚拟传感器,假设模型中共设立k个传感器,且所设立的节点在实际应用中都是可以布设传感器的测试点,虚拟传感器集合 S={s1,s2,…,sk} 。使用传感器特征矩阵(Sensor Signature Matrix,SSM) DSSM 来描述传感器与残差之间的关系,如式(10)所示,矩阵元素 DSSMji 表示残差 ri 的变量集合 Ki 是否包含传感器 Df(e)j 。
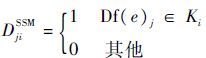 | (10) |
2.3 残差、故障、传感器三者的关系 在2.1和2.2节分析完残差和故障的关系以及残差与传感器的关系后,本文所研究的满足系统检测性和隔离性要求的传感器配置问题可以转化为,如何找到一组传感器集合,使由它和源元件生成的结构性残差可以最大限度地覆盖 AXi 、 DXij 集合,即当残差子空间 X 可以覆盖 AXi 、 DXij 集合时,找到一组对应传感器数量最少的 X′ ,它对应的传感器集合是最优的传感器配置集合 Sopt ;当任何残差子空间都不能覆盖 AXi 、 DXij 集合时,找到一个残差子空间 X′ ,使
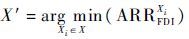 | (11) |
即当残差子空间故障指示度ARRXiFDI最小时,那么这个X′对应的传感器集合就是最大限度满足系统检测性和隔离性要求的最优的传感器配置集合Sopt。
3 应 用 利用同步电机作为本文所提出的键合图传感器布局方法的实验对象,验证在最大限度满足故障监测和隔离的条件下传感器最优配置方案。由于同步电机结构复杂、参数众多、电场磁场耦合程度高,使用公式法推导残差较为复杂,利用键合图模型,在关键的“0/1”节点处设置相应传感器,对于推导残差十分便利。
3.1 同步电机基本参数及传感器位置初步设置 本文采用同步电机[13]作为建模对象,其基本参数如下:额定视在功率Pn=8 100 V·A,额定电压Vn=400 V,频率fn=400 Hz,额定励磁电流ifn=50 A;定子绕组参数:Rs=1.62 Ω,Ll=0.004 527 H,Lmd=0.108 6 H,Lmq=0.051 75 H;励磁绕组参数(折算到定子边):Rf=1.208 Ω,Lf=0.011 32 H,阻尼绕组参数(折算到定子边):RD=3.142 Ω,LD=0.007 334 H,RQ=4.772 Ω,LQ=0.010 15 H。
图 3所示的同步发电机键合图模型[14-15]需要一定的改进后可进行各种故障模拟仿真,具体改进如下:①输出abc端口的“1”节点前加入能量开关节点[16](SPJ)模拟短路开关,SPJ节点是一种用来模拟理想开关器件的节点,它所连接的键中允许存在多个势/流决定键,但在同一时刻类似“0/1”节点只允许使能一个键;②输出abc端口处接入三相负载。
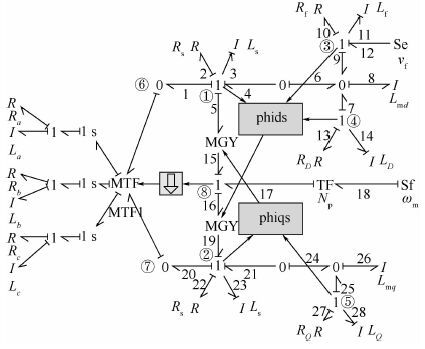 |
| Ra、Rb、Rc —a、b、c相负载电阻; La、Lb、Lc —a、b、c相负载电感;MTF—调制TF; MTF1—调制TF的一种; MGY—调制GY;ωm—机械角速度。 图 3 同步电机键合图模型(发电机惯例)[14-15] Fig. 3 Bond graph model of synchronous machine in generator convention[14-15] |
| 图选项 |
图 4为同步发电机键合图模型基本特性曲线。同步发电机空载特性如图 4(a)所示,在t=0.5 s时设置负载 Ra=Rb=Rc=0 、 La=Lb=Lc= 0,在t=1 s时恢复负载值。图 4(b)所示为同步发电机短路特性,通过控制3个SPJ节点“1 s”的控制信号,模拟输出端短路,在t=0.5 s时闭合SPJ节点,在t=1 s时断开SPJ节点。图 4中: ua和ia 分别为a相电压和电流; uq和iq 分别为q轴等效电压和电流; ud和id 分别为d轴等效电压和电流。
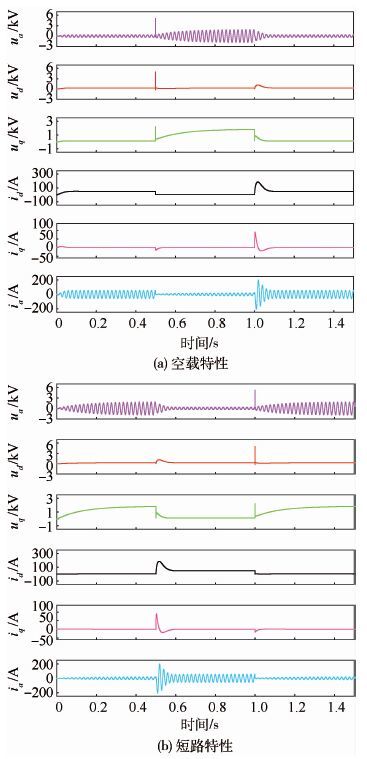 |
| 图 4 同步发电机键合图模型基本特性曲线 Fig. 4 Basic characteristic curves of synchronous generator bond graph model |
| 图选项 |
根据同步发电机模型特点,在图 3中的节点①~⑧处设置虚拟传感器,分别测量 ids、iqs、if、iD、iQ、vds、vqs和ωm ,由此可得系统已知变量集合为
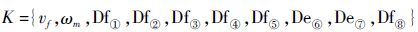 | (12) |
3.2 残差推导 利用第2.2节中式(7)~式(9),图元自身物理性质以及键合图结构信息,消除各键的未知势/流变量。
对于节点①:
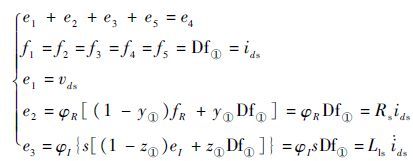 |
对于节点②:
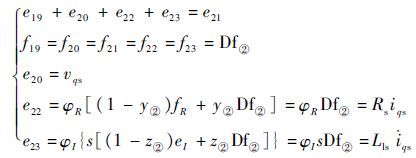 |
对于节点③:
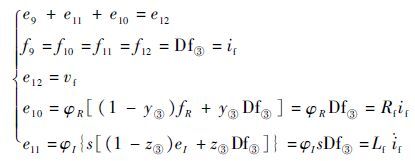 |
对于节点④:
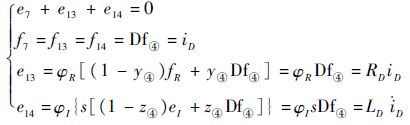 |
对于节点⑤:
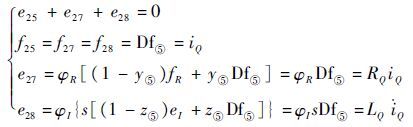 |
对于节点⑧:
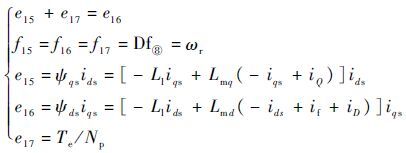 |
式中:Te为电磁转矩。
在实际应用中 v(i)ds、v(i)qs 无法直接测量,可通过测量 v(i)abc ,再经过Park变换后可得到 v(i)ds、v(i)qs ,因此传感器Df①、Df②以及De⑥、De⑦实际为2种传感器。通过3.1节中生成残差的约束方式以及键合图结构信息,消除各键的未知变量,生成系统残差为
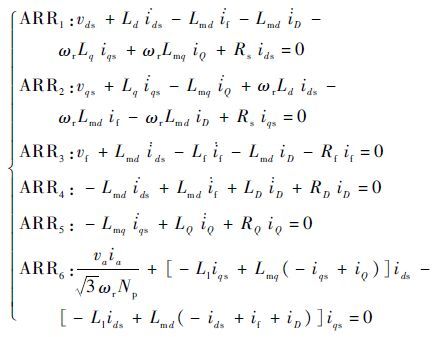 | (13) |
式中: Ld=Ll+Lmd;Lq=Ll+Lmq 。在实际应用中,dq轴阻尼绕组电流 iD、iQ 并不能实际测量到,由它们生成的残差并非结构性残差,因此式(13)中的结构性残差与实际传感器个数相等,只有4个:ARR1、ARR2、ARR3和ARR6。由ARR可推导得出结构故障特征矩阵FSM以及传感器特征矩阵SSM如表 1和表 2所示,假设所有故障严酷度 ρ 一致。
表 1 同步发电机FSM Table 1 FSM of synchronous generator
| 故障 编号 | 故障类型 | ARR | |||||
| r1 | r2 | r3 | r4 | r5 | r6 | ||
| 1 | Rs、Ll、Lmd、Lmq 定子 绕组参数故障 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | RD、RQ、Rf、LD、LQ、Lf转子绕组参数故障 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3 | vf、if输入励磁故障 | 1 | 1 | 1 | 1 | 0 | 1 |
| 4 | ωm 输入转速故障 | 1 | 1 | 0 | 0 | 0 | 1 |
表选项
表 2 同步电机SSM Table 2 SSM of synchronous generator
| 传感器编号 | 传感器类型 | ARR | |||||
| r1 | r2 | r3 | r4 | r5 | r6 | ||
| 1 | Df①、Df②电流传感器 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | Df③励磁电流传感器 | 1 | 1 | 1 | 1 | 0 | 1 |
| 3 | De⑥、De⑦电压传感器 | 1 | 1 | 0 | 0 | 0 | 1 |
| 4 | Df⑧转速传感器 | 1 | 1 | 0 | 0 | 0 | 1 |
表选项
分析表 1可知,不存在全零行残差向量,因此所有故障都是可观测的,但并非所有故障都可隔离,如故障1和故障2的残差向量完全一致,当其中一个故障发生时,无法通过观测残差变化来隔离该故障。将所有模型信息代入3.3节的传感器最优配置集合算法中,得出 X1={r3} , X2={r3,r1} , X3={r3,r2} , X4={r3,r6} 都是在满足最大故障检测和隔离条件下的残差子空间,其中易见 X1 是对数量应最少的传感器残差空间,查找表 2可得,Sopt={Df①,Df②,Df③,Df⑧}为满足最大故障检测和隔离条件下的传感器最优配置集合。
4 结 论 本文在综合分析键合图建模的基本原理基础上提出了一种基于键合图模型的传感器布局优化方法,经同步发电机模型实验验证表明:
1) 模型可实现对同步发电机的基本原理仿真,其开路和短路曲线符合同步电机基本性质。
2) 提出一种残差子空间故障指示度定义,并在此定义基础上提出一种传感器布局优化算法。
3) 通过对同步电机键合图传感器布局仿真,应用本文提出的算法,得到在满足最大故障检测和隔离条件下的传感器最优配置集合。
参考文献
| [1] | MAUL W A, KOPASAKIS G, SANTI L M, et al. Sensor selection and optimization for health assessment of aerospace systems[J]. Journal of Aerospace Computing Information & Communication,2012, 5(1): 16–34. |
| Click to display the text | |
| [2] | KRYSANDER M, FRISK E. Sensor placement for fault diagnosis[J]. IEEE Transactions on Systems and Humans,2008, 38(6): 1398–1410. |
| Click to display the text | |
| [3] | RAGHURAJ R, BHUSHAN M, RENGASWAMY R. Locating sensors in complex chemical plants based on fault diagnostic observability criteria[J]. AIChE Journal,1999, 45(2): 310–322. |
| Click to display the text | |
| [4] | 王中双, 陆念力. 键合图理论及应用研究若干问题的发展及现状[J]. 机械科学与技术,2008, 27(1): 72–77.WANG Z S, LU N L. A review of bond graph theory and its application[J]. Mechanical Science and Technology for Aerospace Engineering,2008, 27(1): 72–77.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | 王艾伦, 刘云. 复杂机电系统动力学相似分析的键合图法[J]. 机械工程学报,2010, 46(1): 74–78.WANG A L, LIU Y. Bond graph method for the dynamic similarity analysis of complex electromechanical system[J]. Journal of Mechanical Engineering,2010, 46(1): 74–78.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [6] | CHATTI N, GEHIN A, OULD B, et al. Functional and behavior models for the supervision of an intelligent and autonomous system[J]. IEEE Transactions on Automation Science & Engineering,2013, 10(2): 431–445. |
| Click to display the text | |
| [7] | CHI G, WANG D, LE T, et al. Sensor placement for fault isolability using low complexity dynamic programming[J]. IEEE Transactions on Automation Science & Engineering,2015, 12(3): 1–12. |
| Click to display the text | |
| [8] | BADOUD A E, KHEMLICHE M, BOUAMAMA B O, et al. Bond graph algorithms for fault detection and isolation in wind energy conversion[J]. Arabian Journal for Science & Engineering,2014, 39(5): 4057–4076. |
| Click to display the text | |
| [9] | KHEMLICHE M, HAFFAF H. Sensor placement for component diagnosability using bond-graph[J]. Sensors & Actuators A:Physical,2006, 132(2): 547–556. |
| Click to display the text | |
| [10] | SAMANTARAY A K, GHOSHAL S K. Sensitivity bond graph approach to multiple fault isolation through parameter estimation[J]. Journal of Systems & Control Engineering,2007, 221(4): 577–587. |
| Click to display the text | |
| [11] | STAROWIECKI M, COMTET G. Analytical redundancy relations for fault detection and isolation in algebraic dynamic systems[J]. Automatica,2001, 37(5): 687–699. |
| Click to display the text | |
| [12] | SAMANTARAY A K, MEDJAHER K, BOUAMAMA B O, et al. Diagnostic bond graphs for online fault detection and isolation[J]. Simulation Modelling Practice & Theory,2006, 14(3): 237–262. |
| Click to display the text | |
| [13] | SAHM D. A two-axis,bond graph model of the dynamics of synchronous electrical machines[J]. Journal of the Franklin Institute,1979, 308(79): 205–218. |
| Click to display the text | |
| [14] | NUNEZ H,ISRAEL N H,BREEDVELD P C,et al.Phasor analysis of a synchronous generator:A bond graph approach[C]//International Journal of Electrical, Computer,Energetic,Electronic and Communication Engineering.Den Haag:World Academy of Science,Engineering and Technology,2014:938-944. |
| Click to display the text | |
| [15] | GONZALEZ G. Analysis of loading effect of systems in a bond graph approach with application to a synchronous machine[J]. Journal of Systems & Control Engineering,2011, 226(2): 243–255. |
| Click to display the text | |
| [16] | JUNCO S, DIéGUEZ G, RAMíREZ F. On commutation modeling in bond graphs[C]//Proceeding of the International Conference on Bond Graph Modeling and Simulation. Vista, CA: The Society for Modeling and Simulation International, 2007: 115-119. |
| Click to display the text | |
