在工程方案选优、质量评估和安全风险评价等决策评价类问题中,多个指标共同参与、进而对决策结果产生影响成为主要特征。如何科学合理地确定每个指标权重是评价方法需要解决的核心问题。一般而言,对决策评价方法科学性的考量应该包含2个方面的因素:①要能够体现作为决策主体的主观意志,即主观因素;②要能够体现具体被评价对象的不同特质,即客观因素。目前常用的决策评价方法有线性分配法、简单加权法、层次分析法(Analytic Hierarchy Process,AHP)、TOPSIS法、ELECTRE法和PROMETHEE法等经典决策评价方法^[1]。****普遍认为,单纯的客观决策评价方法依靠数学规划等手段分析客观数据的内在特点,缺点是忽略了决策者的主观偏好,评价结果往往难以获得决策者的充分认可;单纯的主观决策评价方法则完全依靠决策者的主观判断,缺点是容易造成错误、不一致的判断,并且评价结果极其容易受到决策者认识程度的影响。相比之下,20世纪后期由美国科学家Saaty^[2]提出的层次分析法将决策评价主体的主观判断与客观数据分析相结合,其作为一种经典有效的决策评价工具,具有显著的优越性。
层次分析法由于原理简单,易于理解,应用灵活,在诸多领域得到了广泛的应用。经过多年的发展,又衍生出改进层次分析法、模糊层次分析法、可拓模糊层次分析法和灰色层次分析法等多种方法,并根据研究的实际情况各有其适用的范围^[3]。但是经典层次分析法在实际应用过程中也呈现出了客观性不足、适应性差的缺点。吴殿廷和李东方^[4]对经典层次分析法的不足进行了深度的分析,特别指出层次分析法没有充分利用已有定量信息,对于既有定性指标也有定量指标的问题讨论得不够深入。
此外,在某些领域的评价中,决策者往往希望:当被评价群体某指标值分布相对集中时,由于区分度不高而适当弱化该指标的评价作用;当被评价个体在某指标值较被评价群体有明显优势时,适当强化该指标的导向作用。目前主流的几种层次分析法均不能对决策者的上述需求进行有效回应。本文从以上需求出发,利用被评价对象已有的定量信息对经典的层次分析法进行了修正,提出一种基于层次分析法的自适应决策评价方法(Adaptive evaluation method based on Analytic Hierarchy Process,AAHP)。该方法同时关注权重分配科学性的主观因素和客观因素,能够根据评价群体的变化自适应修正指标权重,有效地弥补了经典层次分析法本身存在的不足,一定程度上提高了决策评价的科学性和适应性。
1 评价指标集的构建和预处理 记A={A₁,A₂,…,A_m}为被评价对象的全体,B={B₁,B₂,…,B_n}为评价指标的全体。
1.1 评价指标集的构建 构建评价指标集B的基本原则为:所选取的评价指标要尽可能反映被评价对象的本质,不能过于复杂但也不能太简单,且它们之间要尽可能相互独立。为此,在具体操作中可以采用如下方法:先照顾评价指标的“多而全”,即将能反映被评价对象的评价指标全部列出,然后利用主分量分析法对所有评价指标进行筛选,剔除冗余(即具有高度相关关系)和不重要的评价指标,得到最终的评价指标集^[5]。
构建完评价指标集B后,记x_ij(1≤i≤m,1≤j≤n)为被评价对象A_i在评价指标B_j下的评分。
1.2 评价值的预处理 评价指标有不同的类型、量纲和量级,并且它们之间的量级差别巨大。鉴于此,为了使评价合理化,需要将所有的评价值进行预处理,目的是消除量纲和量级差,便于评分决策。在实际操作中,通常采用如下标准化方法^[6]:对评价值x_ij,记其标准化之后的值为x_ij^*,则

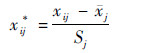(1)

式中:

(2)

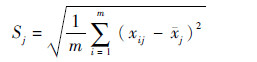(3)

标准化之后的值x_ij^*大部分被压缩在-3~3之间,因此标准化方法起到了某种“惩罚函数”的作用。将标准化的评价值组成的矩阵X^*=(x_ij^*)_m×n称为决策矩阵。
2 评价指标的自适应赋权 利用层次分析法获得指标集权重,然后结合被评价对象本身的数据信息,即决策矩阵所蕴含的信息,自适应地给出评价指标集关于该组被评价对象的动态权重。
2.1 层次分析法确权及数据修正 由经典的层次分析法^[7-8],即建立递阶层次结构、利用专家评分意见构造满足一致性条件的判断矩阵,可确定出评价指标集B中每一个评价指标B_j的权重w_j⁽¹⁾,从而得到权重向量:

(4)

利用这一权重向量,可以对决策矩阵X^*=(x_ij^*)_m×n修正如下:

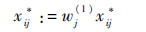(5)

得到的决策矩阵仍记为X^*=(x_ij^*)_m×n。
2.2 权重的自适应修正 为了改善经典层次分析法自身的不足,期望被评价对象指标值相对集中的指标(一般来讲为区分度低、非稀缺性指标)的权重有所下降,相对分散的指标(一般来讲为区分度高、稀缺性指标)的权重有所上升,这就需要依据决策矩阵对层次分析法所给的权重进行自适应修正。
在利用层次分析法给出的权重对决策矩阵进行修正之后,上述想法等价于寻找一组新的权重W⁽²⁾=(w₁⁽²⁾,w₂⁽²⁾,…,w_n⁽²⁾),使得在该组权重下,被评价对象的评分值最为分散。为了衡量精确及数学处理的方便,选用方差作为衡量评分值分散程度的统计量,即要求:

(6)

式中:v_i为被评价对象A_i的评分。
为了得到目标函数式(6)的精确表达,需要给出评分值v_i关于权重w_j⁽²⁾的表达式。一般地,取评分值v_i为关于权重w_j⁽²⁾的线性组合^[5]:

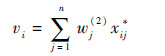(7)

此时,

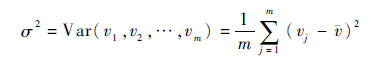(8)

式中:

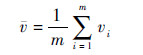(9)

将式(9)代入式(8)并进行简单的求和变换,可得

(10)

式中:

(11)

令

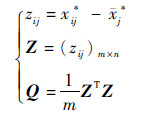(12)

则

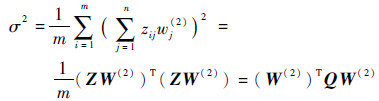(13)

综合以上讨论,得到权重的自适应修正方程为

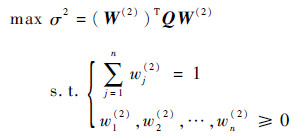(14)

并将通过方程组(14)确定的权重向量W⁽²⁾作为最终的权重向量。
注意到,指标的稀缺程度一方面会随时间发生变化,另一方面也会随不同的被评价群体发生变化。但无论是哪种情况,这些变化都会反映在被评价对象的决策矩阵中(即评价值中),而上述方法充分利用了决策矩阵的信息,因此其可以自适应地在经典的层次分析法的基础上对指标的稀缺程度进行强化或者弱化。
2.3 利用加性加权法计算评分 取第i个被评价对象A_i最后的评分为

(15)

依据这一评分,可以得出各被评价对象的排名。
3 实例应用 合成孔径雷达(Synthetic Aperture Radar,SAR)成像不受光线、天气等因素的影响,可以实现全天时、全天候工作,在目标检测、识别和跟踪等领域有着广泛的应用前景。斑点噪声作为影响SAR图像解译的重要因素,一直是遥感领域的研究热点。目前,常见的降斑算法主要集中在空域和频域,例如Lee滤波、Kuan滤波、Frost滤波、Gamma MAP滤波、PPB和SAR-BM3D。随着研究的深入,小波收缩(wavelet shrinkage)变换以及基于小波变换的二维S变换(Two Dimensional S Transform,TDST)^[9]滤波在SAR图像降斑上取得了不错的效果。各种降斑算法在对SAR图像的实际处理过程中表现各有优劣,而目前对这些算法降斑效果的评价主要依靠对图像的视觉观察或单个指标间对比,没有一种更为综合、客观的评价方法。此外,各类降斑算法对于不同特征的图像也各有适用性,需要一种能够反应被处理图像自身信息的评价方法来对其处理效果进行评价。本文先尝试建立一个SAR图像降斑算法的评价指标体系,然后用本文提出的方法对几个主流的降斑算法进行综合评价。
3.1 SAR图像降斑算法评价指标体系 当前常用的评价降斑效果的指标主要包括等效视数(Equivalent Number of Look,ENL)^[10]、边缘保持系数(Edge Preservation Index,EPI)^[11]、信杂比(Target to Clutter Ratio,TCR)^[12]、比图像均值(Expectation of Ratio Image,ERI)^[13]和峰值信噪比(Peak Signal to Noise Ratio,PSNR)等。
为了对降斑算法进行全面客观的评价,建立如表 1所示的降斑算法评价指标体系。
表 1 降斑算法评价指标体系 Table 1 Evaluation index system of despeckling algorithm

准则层A	指标层B	指标描述
平滑能力 (A1)	ENL(B1)	评价均匀区域平滑效果,数值越大,平滑能力越强
细节保留 (A2)	EPI(B2)	描述细节保存的能力,数值越大,细节信息丢失越少
	TCR(B3)	描述点目标的保存能力,数值越大,效果越好
噪声影响 (A3)	ERI(B4)	描述噪声的分布,数值越接近1,说明越接近Γ分布
	PSNR(B5)	数值越大,降噪效果越好(假设每幅图像都能找到原图)

表选项






同时,选取图 1(a)和图 2(a)2幅SAR图像(白色方块区域用于计算TCR),分别用Lee滤波、PPB、SAR-BM3D、小波收缩变换和TDST滤波5种算法进行降斑处理,处理结果如图 1和图 2所示。5种降斑算法对应于表 1评价指标体系中的各项指标值如表 2和表 3所示。

图 1 SAR图像1及其降斑图像 Fig. 1 Image 1 of SAR and its despeckling images

图选项

图 2 SAR图像2及其降斑图像 Fig. 2 Image 2 of SAR and its despeckling images

图选项

表 2 5种降斑算法处理图 1(a)指标数据 Table 2 Index data of Fig. 1(a) with 5 kinds of despeckling algorithm treatment

指标	Lee滤波	PPB	SAR-BM3D	小波收 缩变换	TDST滤波
B1(ENL)	1.747 8	1.100 4	1.527 9	1.471 3	1.458 2
B2(EPI)	0.216 5	0.657 4	0.408 0	0.300 6	0.302 4
B3(TCR)	9.649 9	12.409 7	10.290 0	11.111 9	10.771 2
B4(ERI)	0.971 0	0.998 4	0.838 9	1.055 0	1.082 6
B5(PSNR)	21.272 9	24.000 0	23.703 7	21.894 1	21.932 8

表选项






表 3 5种降斑算法处理图 2(a)指标数据 Table 3 Index data of Fig. 2(a) with 5 kinds of despeckling algorithm treatment

指标	Lee滤波	PPB	SAR-BM3D	小波收 缩变换	TDST滤波
B1(ENL)	2.799 7	1.738 9	2.659 1	2.606 3	2.591 7
B2(EPI)	0.119 4	0.675 6	0.097 7	0.138 7	0.142 8
B3(TCR)	8.554 9	12.977 7	9.319 7	10.101 5	9.781 5
B4(ERI)	1.000 5	1.008 4	0.907 5	1.003 4	1.004 3
B5(PSNR)	21.089 2	22.000 0	21.062 5	21.366 3	21.259 9

表选项






3.2 评价结果对比及分析
3.2.1 层次分析法和本文方法的权重变化对比分析 本研究邀请了10位专门从事SAR图像理解领域研究的教授对SAR图像降斑算法的评价指标体系中每一层次的各指标的相对重要性进行两两比较,评价的结果按1~9判断尺度加以量化,得到判断矩阵。先对判断矩阵进行一致性检验,由于一致性指标CR <0.1,因此由10位专家评分得到的判断矩阵具有满意的一致性。然后按照层次分析法赋权法和本文方法赋权法分别得到对图 1(a)降斑算法的评价指标体系的层次分析法权重和本文方法权重,如表 4所示。
表 4 2种评价方法所得权重的对比 Table 4 Comparison of weights resulting from two evaluation methods

指标	层次分析法权重	本文方法权重	绝对变化
B1(ENL)	0.292 1	0.248 3	-0.043 8
B2(EPI)	0.120 1	0.138 1	0.018 0
B3(TCR)	0.070 5	0.081 1	0.010 6
B4(ERI)	0.101 6	0.086 4	-0.015 2
B5(PSNR)	0.415 7	0.446 2	0.030 5

表选项






从表 4可以看出,ENL和ERI 2个指标在原有专家评分(即层次分析法权重)的基础上权重有所降低,而EPI、TCR和PSNR 3个指标的权重有所提升。这与从表 2中对于各种算法的指标值分布特征的观察结果是一致的。如ERI,各算法的指标值相对集中,表明各算法在此项指标上的表现差异不大,因此希望该指标的权重适当降低以弱化其评价作用;再如PSNR,其是比较明显的稀缺性指标,PPB和SAR-BM3D在该指标下的表现明显优于其他指标,因此本文方法给出的权重高于经典的层次分析法,从而有效地体现出了稀缺性指标的导向作用。此外,本文方法对于指标权重的修正幅度不大,在可接受范围内。

3.2.2 本文方法对降斑算法的评价结果分析 表 5给出运用本文方法对5种降斑算法降斑效果的评价结果。
表 5 本文方法下各种降斑算法的评分及排序 Table 5 Rating and ranking of various kinds of despeckling algorithm within AAHP

算法	图 1(a) 评分	图 1(a) 排序	图 2(a) 评分	图 2(a) 排序
Lee滤波	-0.380 240	5	-0.240 830	3
PPB	0.654 673	1	0.505 191	1
SAR-BM3D	0.378 801	2	0.336 952	2
小波收缩变换	-0.290 820	3	-0.260 950	4
TDST滤波	-0.362 410	4	-0.340 360	5

表选项






从表 5中评价结果可以看出,PPB和SAR-BM3D 2种算法对2幅SAR图像的处理效果都有较好的评价结果,其他算法对于2幅图像处理结果的评价略有差异,这也体现出不同算法对于不同类型图像的处理能力各不相同。如Lee滤波算法对于图 2(a)的处理效果要好于图 1(a),说明其更适合于均匀SAR图像的降斑处理。
就降斑算法理论而言,PPB算法基于非局部均值滤波器,在低信噪比条件下,其迭代算法能够有效提升SAR图像的降斑效果,在均匀区域的平滑以及细节保存方面都有着良好的表现^[14]。SAR-BM3D算法采用相似性度量,综合考虑了斑点噪声的概率分布以及三维空间内的小波收缩,但由于现阶段斑点噪声统计模型的不足造成其适应性要弱于PPB算法^[15-16]。基于小波变换的TDST滤波算法,其在核心算法上与小波收缩变换算法是相似的,导致两者的降斑效果在一定程度上也是相似的^[9],作为经典的局部统计滤波器的一员,其局限性在于滑动窗口的尺寸是固定的,导致算法的适应性不强,在平滑和细节保存方面没有做到很好的平衡^[16-17]。这些特点均与本文评价结果吻合,从而验证了基于层次分析法的自适应决策评价方法的有效性。
4 结论 本文基于经典层次分析法提出了一种能够根据被评价群体数据分布特征自适应修正权重的评价决策方法。通过对多种SAR图像降斑算法的评价实例,验证了该评价方法的如下特点:
1) 本文方法利用被评价群体的指标值修正决策矩阵,因此在评价过程中包含了被评价对象的自身信息,较经典的层次分析法更为客观,特别适用于对算法、方法等处理对象差异性大的对象(如本文中提到的降斑算法评价)的评价或需要考虑在评价结果中体现政策、时间等因素影响的评价过程(如绩效评估)。
2) 指标值分布相对集中时,将降低该指标的基础权重;被评价个体在某指标值较被评价群体有明显优势时,将提升该指标的基础权重。从而有效体现稀缺性指标在评价体系中的导向作用。
3) 指标权重修正幅度不大,在可接受范围内,由专家主观判断产生的指标权重在决策评价过程中仍然占据主导地位。
基于以上特点,本文方法可有效适用于各类决策评价中决策者希望体现稀缺指标的导向和激励作用或者凸显指标值离散度高的指标的情况,如通过关键业绩指标进行业绩排序或绩效分配。同时需要特别指出的是,本文方法对稀缺性指标的评判主要依据被评价群体的数据分布特征,但某些情况下,数据分散程度不能与指标稀缺程度完全匹配。在以后的研究中需要考虑如何修正权重以准确体现指标的稀缺性,以期找到一种自适应性更强的评价决策方法。

参考文献

[1]	朱建军. 层次分析法的若干问题研究及应用[D].沈阳:东北大学,2005:16-25. ZHU J J.Research on several problems of analytic hierarchy process and its applications[D].Shenyang:Northeastern University,2005:16-25.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[2]	SAATY T L. Decision making for leaders:The analytical hierarchy process for decisions in a complex world[M].Belmont : Wadsworth , 1982: 28-42.
	Click to display the text
[3]	郭金玉, 张忠彬, 孙庆云. 层次分析法的研究与应用[J]. 中国安全科学学报,2008, 18(5): 148–153.GUO J Y, ZHANG Z B, SUN Q Y. Research and application on analytic hierarchy process[J]. China Safety Science Journal,2008, 18(5): 148–153.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[4]	吴殿廷, 李东方. 层次分析法的不足及其改进的途径[J]. 北京师范大学学报(自然科学版),2004, 40(2): 264–268.WU D T, LI D F. The shortage and improvement approach for the analytic hierarchy process[J]. Journal of Beijing Normal University(Nature Science),2004, 40(2): 264–268.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[5]	熊伟. 运筹学 3版[M].北京 : 机械工业出版社, 2014: 89-120.XIONG W. Operations research 3rd[M].Beijing : Mechanical Industry Press , 2014: 89-120.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[6]	徐光辉. 运筹学基础手册[M]. 北京: 科学出版社 , 1999: 43-85.XU G H. Handbook of operations research[M].Beijing : Science Press , 1999: 43-85.(in Chinese).
	Cited By in Cnki (0) | Click to display the text
[7]	SAATY T L, ALEXANDER J. Conflict resolution:The analytic hierarchy process[M]. New York: Praeger , 1989: 56-118.
	Click to display the text
[8]	SAATY T L, VARGAS L G. Models,methods,concepts & applications of the analytic hierarchy process[M].New York : Kluwer Academic , 2001: 22-73.
	Click to display the text
[9]	GAO F, XUE X, SUN J, et al. A SAR image despeckling method based on two-dimensional S transform shrinkage[J]. IEEE Transactions on Geoscience and Remote Sensing,2016, 54(5): 3025–3034.
	Click to display the text
[10]	LEE J S. Speckle analysis and smoothing of synthetic aperture radar images[J]. Computer Graphics & Image Processing,1981, 17(1): 24–32.
	Click to display the text
[11]	LEE J S, JURKEVICH L, DEWAELE P, et al. Speckle filtering of synthetic aperture radar images:A review[J]. Remote Sensing Reviews,1994, 8(4): 255–267.
	Click to display the text
[12]	BENITZ G R. High-definition vector imaging[J]. Lincoln Laboratory Journal,1997, 10(2): 147–169.
	Click to display the text
[13]	OLIVER C J, QUEGAN S. Understanding synthetic aperture radar images[M].Norwood : Artech House , 1998: 65-128.
	Click to display the text
[14]	DELEDALLE C A, DENIS L, TUPIN F. Iterative weighted maximum likelihood denoising with probabilistic patch-based weights[J]. IEEE Transactions on Image Processing,2009, 18(12): 2661–2672.
	Click to display the text
[15]	PARRILLI S, PODERICO M, ANGELINO C V, et al. A nonlocal SAR image denoising algorithm based on LLMMSE wavelet shrinkage[J]. IEEE Transactions on Geoscience & Remote Sensing,2012, 50(2): 606–616.
	Click to display the text
[16]	ARGENTI F, LAPINI A, BIANCHI T, et al. A tutorial on speckle reduction in synthetic aperture radar images[J]. IEEE Geoscience & Remote Sensing Magazine,2013, 1(3): 6–35.
	Click to display the text
[17]	LEE J S. Refined filtering of image noise using local statistics[J]. Computer Graphics & Image Processing,1981, 15(4): 380–389.
	Click to display the text